Все ошибки выборочного наблюдения подразделяются на ошибки выборки (случайные); ошибки, вызванные отклонениями от схемы отбора (неслучайные); ошибки наблюдения (случайные и неслучайные).
Случайные ошибки – те, которые изменяются по вероятностным законам. К случайным относится ошибка выборки.
Ошибка выборки или ошибка репрезентативности – это разница между значением показателя, полученного по выборке, и генеральным параметром.
Средняя ошибка выборки зависит от объема выборки и степени вариации признака в генеральной совокупности. Уменьшение ошибки выборки, а следовательно, увеличение точности оценки, всегда связано с увеличением объема выборки. В этой связи уже на стадии организации выборочного наблюдения приходится решать вопрос о том, каков должен быть объем выборочной совокупности, чтобы была обеспечена требуемая точность результатов наблюдения.
Вид выборки также влияет на величину ошибки выборки. Формулы расчета средней ошибки и необходимой численности выборки при различных видах выборки представлены в табл. 6.2.
Предельная ошибка выборки связана с заданным уровнем вероятности. С учетом выбранного уровня вероятности и соответствующего ему значения t предельная ошибка выборки рассчитывается по формуле:
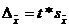 (6.1)
(6.1)
Тогда можно утверждать, что при заданной вероятности генеральная средняя будет находиться в следующих границах:
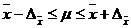 (6.2)
(6.2)
Таблица 6.2
Формулы расчета средней ошибки и объема выборки
| Вид
выборки
| Средняя ошибка выборки (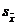 ) )
| Объем выборки (k)
|
| повторной
| бесповторной
| повторной
| бесповторной
|
| Случайная
(механическая)
| 
| 
| 
| 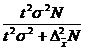
|
 – допустимая погрешность, которая задается исследователем исходя из требуемой точности результатов проектируемой выборки; – допустимая погрешность, которая задается исследователем исходя из требуемой точности результатов проектируемой выборки;
 – табличная величина, соответствующая заданной доверительной вероятности F(t), с которой будут гарантированы оценки генеральной совокупности по данным выборочного обследования; – табличная величина, соответствующая заданной доверительной вероятности F(t), с которой будут гарантированы оценки генеральной совокупности по данным выборочного обследования;
 - генеральная дисперсия. - генеральная дисперсия.
|
| Типическая
| 
| 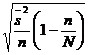
| 
| 
|
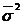 – средняя из внутригрупповых дисперсий – средняя из внутригрупповых дисперсий
|
| Серийная
| 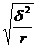
| 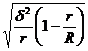
| 
| 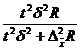
|
 – число отобранных серий; – число отобранных серий;
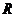 – общее число серий – общее число серий
 – межгрупповая дисперсия: – межгрупповая дисперсия:
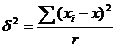 , ,
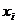 – средняя i-й серии;
x – общая средняя по всей выборочной совокупности – средняя i-й серии;
x – общая средняя по всей выборочной совокупности
|
Пример 1. В результате выборочного обследования работников организации осуществленного на основе собственно-случайной повторной выборки, получен следующий ряд распределения (табл. 6.3).
Таблица 6.3. Результаты выборочного обследования работников организации
| Возраст, лет
| До 25
| 25 – 35
| 35 – 45
| 45 – 55
| 55 и более
|
| Численность работников данного возраста
|
|
|
|
|
|
С вероятностью 0,954 определите границы среднего возраста работников организации.
Для определения средней ошибки выборки необходимо прежде всего рассчитать выборочную среднюю величину и дисперсию изучаемого признака. Информация для расчета данных показателей представлена в табл. 6.4
Таблица 6.4. Расчет среднего возраста работников организации и дисперсии
| Возраст, лет
| Численность лиц данного возраста
| Середина интервала
| 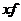
| 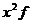
|
| До 25
25 – 35
35 – 45
45 – 55
55 и более
|
|
|
|
|
| Итого
|
| –
|
|
|
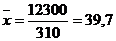
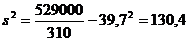
Среднюю ошибку выборки рассчитаем по формуле, представленной в табл. 6.1:
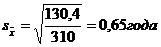
Определим по формуле (6.1) предельную ошибку выборки с вероятностью 0,954 (t = 2):
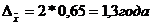
Установим границы генеральной средней, используя формулу (6.2):
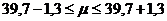
или
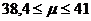
Таким образом, на основании проведенного выборочного обследования с вероятностью 0,954 можно заключить, что средний возраст работников организации лежит в пределах от 38 до 41 года.
Пример 2. Определите, сколько учащихся первых классов школ района необходимо отобрать в порядке собственно-случайной бесповторной выборки, чтобы с вероятностью 0,997 определить границы среднего роста первоклассников с предельной ошибкой 2 см. Известно, что всего в первых классах школ района обучается 1100 учеников, а дисперсия роста по результатам аналогичного обследования в другом районе составляет 24.
Для определения объема собственно-случайной бесповторной выборки будем использовать формулу, представленную в табл. 6.1. Необходимый объем выборки при уровне вероятности 0,997 (t = 3) составит:
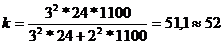
Таким образом, для получения данных о среднем росте первоклассников с заданной точностью необходимо обследовать 52 школьника.
Пример 3. В целях изучения доходов населения по трем районам области сформирована 2%-ная выборка, пропорциональная численности населения этих районов. Полученные результаты представлены в табл. 6.5.
Таблица 6.5
Результаты выборочного обследования доходов населения
| Район
| Численность
населения, чел.
| Обследовано, чел.
| Доход в расчете на 1 человека
|
| средняя, тыс. р.
| дисперсия
|
| I
II
III
|
|
| 2,9
2,5
2,7
| 1,3
1,1
1,6
|
Определите границы среднедушевых доходов населения по области в целом при уровне вероятности 0,997.
Рассчитаем среднюю из внутригрупповых дисперсий:
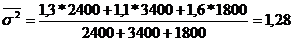
Рассчитаем среднюю ошибку типической бесповторной выборки по формуле, представленной в табл. 6.1:
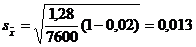
Определим по формуле (6.1) предельную ошибку выборки с вероятностью 0,997 (t = 3):
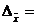 3*0,013 = 0,039
3*0,013 = 0,039
Рассчитаем выборочную среднюю:
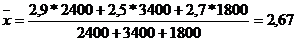
В результате проведенных расчетов с вероятностью 0,997 можно сделать вывод, что среднедушевые доходы жителей данной области находятся в следующих границах (тыс. руб.)
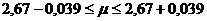
Пример 4. В целях контроля качества комплектующих из партии изделий, упакованных в 50 ящиков по 20 изделий в каждом, была произведена 10%-ная серийная выборка. По попавшим в выборку ящикам среднее отклонение параметров изделия от нормы соответственно составило 9 мм, 11, 12, 8 м 14 мм. С вероятностью 0,954 определите среднее отклонение параметров по всей партии в целом.
Рассчитаем выборочную среднюю:
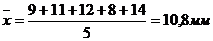
Определим величину межгрупповой дисперсии (формула представлена в табл. 6.1):
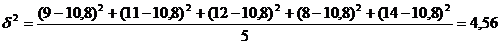
С учетом установленной вероятности Р = 0,954 (t = 2) средняя ошибка выборки составит (формула расчета средней ошибки серийной бесповторной выборки представлена в табл. 6.1):
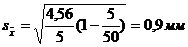 ,
,
а предельная ошибка выборки составит:
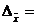 2*0,9 = 1,8 мм
2*0,9 = 1,8 мм
Произведенные расчеты позволяют заключить, что среднее отклонение параметров всех изделий от нормы находятся в следующих границах:
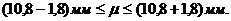
Контрольные вопросы
1. Перечислите основные причины использования выборочного наблюдения.
2. В чем различие между генеральной и выборочной совокупностями?
3. Какие виды отбора единиц из генеральной совокупности вы знаете?
4. Напишите формулы расчета средней ошибки и объема бесповторной выборки.
5. Напишите формулы расчета средней ошибки и объема повторной выборки.





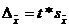 (6.1)
(6.1)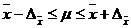 (6.2)
(6.2)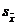 )
)



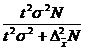
 – допустимая погрешность, которая задается исследователем исходя из требуемой точности результатов проектируемой выборки;
– допустимая погрешность, которая задается исследователем исходя из требуемой точности результатов проектируемой выборки;
 – табличная величина, соответствующая заданной доверительной вероятности F(t), с которой будут гарантированы оценки генеральной совокупности по данным выборочного обследования;
– табличная величина, соответствующая заданной доверительной вероятности F(t), с которой будут гарантированы оценки генеральной совокупности по данным выборочного обследования;
 - генеральная дисперсия.
- генеральная дисперсия.

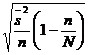


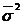 – средняя из внутригрупповых дисперсий
– средняя из внутригрупповых дисперсий
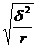
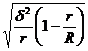
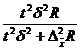
 – число отобранных серий;
– число отобранных серий;
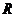 – общее число серий
– общее число серий
 – межгрупповая дисперсия:
– межгрупповая дисперсия:
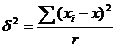 ,
,
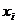 – средняя i-й серии;
x – общая средняя по всей выборочной совокупности
– средняя i-й серии;
x – общая средняя по всей выборочной совокупности
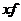
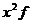
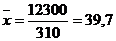
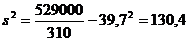
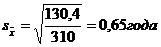
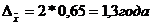
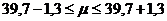
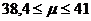
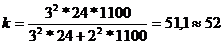
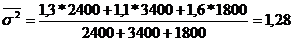
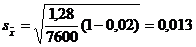
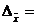 3*0,013 = 0,039
3*0,013 = 0,039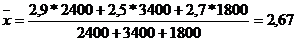
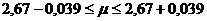
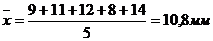
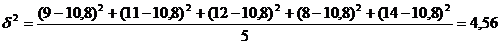
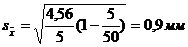 ,
,