

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает...
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует...
Интересное:
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Основные правила дифференцирования
1.  .
.
2.  независимая переменная.
независимая переменная.
3.  , где
, где  .
.
4.  ,
,  .
.
5.  ,
,
 .
.
6.  .
.
7. Производная сложной функции. Если  , где
, где  .
.
8. Дифференциал функции. Если  .
.
Таблица производных
1. Производная степенной функции 
 . Частные случаи:
. Частные случаи:  .
.
2. Производная показательной функции  ,
,
 ;
;  , так как
, так как  ;
;  , так как
, так как  .
.
3. Производная логарифмической функции 
 ;
; 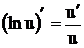 , так как
, так как  ;
;  , так как
, так как  .
.
4. Производные тригонометрических функций
 ;
;  ;
; 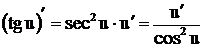 ;
;
 ;
;  ;
;
 .
.
5. Производные обратных тригонометрических функций:
 ,
,  ,
,
 ,
,  .
.
6. Производные гиперболических функций:
 ,
,  ,
,
 ,
,  .
.
Неопределенный интеграл
Теорема существования. Если функция  непрерывна в заданном промежутке
непрерывна в заданном промежутке  , то в этом промежутке она имеет первообразную.
, то в этом промежутке она имеет первообразную.
Основные свойства неопределенного интеграла
1.  . 2.
. 2.  .
.
3.  . 4.
. 4.  .
.
5.  .
.
6. Если  , то
, то  .
.
7. Если  , то
, то  .
.
8. Если  , то
, то  .
.
Методы интегрирования
1. Метод замены переменной (способ подстановки)
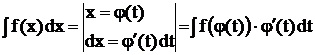 .
.
2. Метод интегрирования по частям: 
 .
.
Таблица неопределенных интегралов
1. Интеграл от степенной функции  :
:
 ; (1)
; (1)  . (2)
. (2)
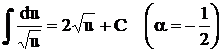 . (3)
. (3)
2.  .
.
3. Интеграл от показательной функции  :
:
 .
.
4. Интегралы от тригонометрических функций:
 ;
;  ;
;
 ;
;  ;
;  ;
;  ;
;
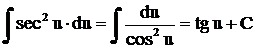 ;
;  .
.
5. Интегралы от гиперболических функций:
 ;
;  ;
;
 ;
;  .
.
6. Интегралы, содержащие выражение вида  :
:
 . (5)
. (5)  . (6)
. (6)
 . (7)
. (7)  . (8)
. (8)
 . (9)
. (9)  . (10)
. (10)
7. Часто встречающиеся интегралы:
 .
.
 .
.
 . (11)
. (11)
 . (12)
. (12)
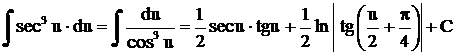 . (13)
. (13)
 . (14)
. (14)
8. Реккурентные соотношения
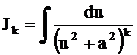 ;
;  . (15)
. (15)
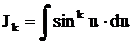 ;
;  .
.
 ;
;  .
.
Замечание
1. Во всех формулах подынтегральные функции предполагаются сложными,
т. е. аргумент и есть некоторая функция от независимой переменной х:  . Следует хорошо уяснить, что все формулы верны лишь в том случае, когда подынтегральная функция умножается строго на дифференциал аргумента u, т. е. на
. Следует хорошо уяснить, что все формулы верны лишь в том случае, когда подынтегральная функция умножается строго на дифференциал аргумента u, т. е. на  . Так, например,
. Так, например,  , но
, но  , так как здесь
, так как здесь  , чего нет под интегралом. Аналогично
, чего нет под интегралом. Аналогично  , но
, но  , так как здесь
, так как здесь 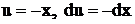 , чего нет под интегралом.
, чего нет под интегралом.
|
|
Для упрощения записи во всех формулах независимая переменная х опущена. Например, формула (1) имеет следующий вид:  . Такая запись затрудняет запоминание формулы.
. Такая запись затрудняет запоминание формулы.
2. Вся таблица интегралов разбита на восемь групп формул. Деление это, вообще говоря, произвольное, сделано с единственной целью, чтобы можно было быстрее и легче запомнить эти формулы. Впрочем, в большинстве случаев достаточно знать первые шесть групп формул. Седьмая группа выделена потому, что эти интегралы находятся достаточно длинным способом и встречаются на практике редко.
3. Следует научиться работать с рекуррентными соотношениями. Сущность их состоит в том, что, зная интеграл 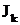 , можно без труда найти интеграл
, можно без труда найти интеграл 
Приведем пример использования формулы (15). Полагая здесь 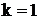 , получим
, получим
 (табличный интеграл (5)),
(табличный интеграл (5)),
 ,
,  .
.
При  имеем
имеем  ,
,
 ,
,
 .
.
В заключение отметим, что существуют три способа отыскания неопределенных интегралов: интегрирование с помощью табличных формул (он называется иначе «метод подведения под знак дифференциала»), метод замены переменной (иначе: «способ подстановки») и метод интегрирования по частям. Подробно рассмотрим эти методы.
Упражнения (устно)
Дайте ответы в следующих примерах.

 .
.
Упражнение
Найти следующие интегралы.







Задание на дом

Примеры.


 .
.
Последний интеграл степенной, так как  , если
, если
 , поэтому
, поэтому

 .
.
 .
.

Первый интеграл степенной:  , где
, где  . Второй интеграл также степенной, его можно найти в примере
. Второй интеграл также степенной, его можно найти в примере  . Поэтому
. Поэтому
 .
.

Упражнение. Решить примеры.

Упражнение
Найти интегралы

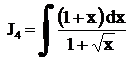 ,
,  .
.
Примеры
Многочлен  имеет простые вещественные корни
имеет простые вещественные корни
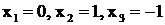 .
.
Решение. Многочлен 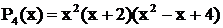 имеет вещественный простой корень
имеет вещественный простой корень  ; двукратный корень
; двукратный корень 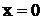 .
.
Определение. Следующие рациональные дроби называются простейшими первого, второго, третьего и четвертого типов: 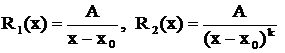
|
|
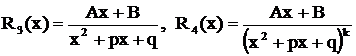 .
.
Здесь 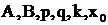 - заданные числа,
- заданные числа, 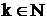 .
.
В последующем постоянно предполагается, что трехчлен 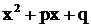 не имеет
не имеет
вещественных корней и, следовательно, не разлагается на линейные множители.
Примеры. Рассмотрим дроби
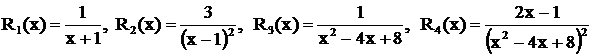 .
.
Здесь 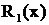 - дробь первого типа, причем
- дробь первого типа, причем  - дробь второго типа, где
- дробь второго типа, где 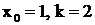 .
. 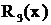 - дробь третьего типа, где
- дробь третьего типа, где 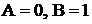 , причем трехчлен
, причем трехчлен  вещественных корней не имеет. Дробь
вещественных корней не имеет. Дробь 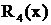 принадлежит к четвертому типом, где
принадлежит к четвертому типом, где 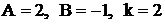 .
.
Дроби 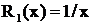 и
и 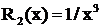 принадлежат соответственно к первому и второму типам, причем
принадлежат соответственно к первому и второму типам, причем 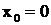 .
.
Теорема о разложении рациональной дроби. Всякая правильная рациональная дробь разлагается в сумму простейших дробей первого – четвертого типов. При этом если 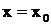 - простой вещественный корень знаменателя
- простой вещественный корень знаменателя 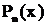 , то в разложении ему соответствует дробь первого типа
, то в разложении ему соответствует дробь первого типа 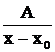 ; если
; если 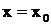 - вещественный корень кратностью k, то в разложении ему соответствует сумма k дробей первого и второго типов:
- вещественный корень кратностью k, то в разложении ему соответствует сумма k дробей первого и второго типов:
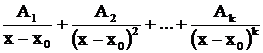 ; если в знаменателе
; если в знаменателе 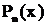 имеется трехчлен
имеется трехчлен 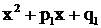 без вещественных корней, то в разложении дроби ему соответствует дробь третьего типа
без вещественных корней, то в разложении дроби ему соответствует дробь третьего типа 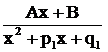 ; если, наконец, знаменатель
; если, наконец, знаменатель 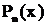 содержит множитель
содержит множитель 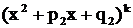 , то в разложении ему соответствует сумма «k» дробей третьего и четвертого типов:
, то в разложении ему соответствует сумма «k» дробей третьего и четвертого типов: 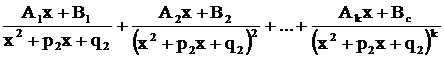 .
.
Таким образом, разложение дроби 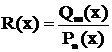 существенно зависит от того, какие корни имеет знаменатель
существенно зависит от того, какие корни имеет знаменатель 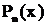 . Поэтому разложение рекомендуется проводить по следующей схеме.
. Поэтому разложение рекомендуется проводить по следующей схеме.
1. Найти все корни знаменателя 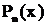 и определить их кратность.
и определить их кратность.
2. Написать разложение 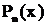 на линейные и квадратные множители.
на линейные и квадратные множители.
3. Написать сумму простейших дробей в соответствии с полученным разложе-нием знаменателя.
Пример 1. Разложить дробь 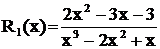 .
.
Решение. Здесь знаменатель имеет разложение 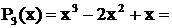
 . Отсюда следует, что
. Отсюда следует, что  - простой вещественный корень, ему соответствует дробь
- простой вещественный корень, ему соответствует дробь 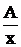 ;
; 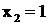 - вещественный двукратный корень, ему соответствует сумма дробей
- вещественный двукратный корень, ему соответствует сумма дробей 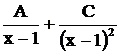 . Поэтому данная дробь представлена суммой
. Поэтому данная дробь представлена суммой 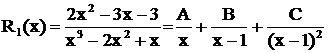 .
.
Пример 2. Разложить дробь 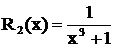 .
.
Решение. Здесь  , причем трехчлен вещественных корней не имеет, поэтому
, причем трехчлен вещественных корней не имеет, поэтому  .
.
Пример 3. Разложить дробь  .
.
Решение. Здесь знаменатель 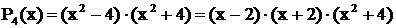
имеет вещественные простые корни: 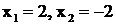 . Двучлен
. Двучлен  веществен-ных корней не имеет: если
веществен-ных корней не имеет: если  , то
, то 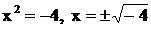 . Поэтому разло-жение дроби имеет вид
. Поэтому разло-жение дроби имеет вид
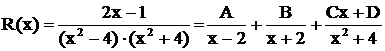 .
.
Теперь перейдем к нахождению неопределенных коэффициентов разложения: А, В, С,…. Существуют два способа их определения. Поскольку оба способа достаточно простые, рассмотрим их на конкретных примерах.
Первый способ. Дробь 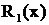 представлена в виде
представлена в виде
|
|
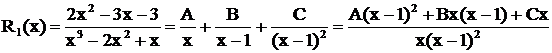 .
.
Поскольку здесь знаменатели равны, то должны быть равны и числители.
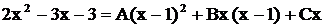 . Имеет место равенство двух многочленов, которое выполняется тождественно, т.е. при любых значениям «х».
. Имеет место равенство двух многочленов, которое выполняется тождественно, т.е. при любых значениям «х».
Пусть, например, 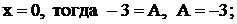 при
при 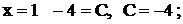 при
при  . Таким образом, получили разложение дроби
. Таким образом, получили разложение дроби  .
.
Замечание. Нахождение неопределенных коэффициентов А, В, С, … упрощается, если в качестве значений «х» брать корни знаменателя.
Второй способ покажем на следующем примере:
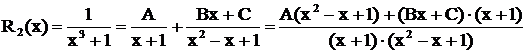 ,
,
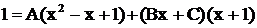 . В правой части раскроем скобки и приведем подобные члены, тогда
. В правой части раскроем скобки и приведем подобные члены, тогда  или
или 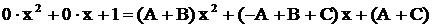 . Приравнивая коэффициенты при одинаковых степенях х и свободные члены, получаем систему линейных уравнений относительно А, В, С:
. Приравнивая коэффициенты при одинаковых степенях х и свободные члены, получаем систему линейных уравнений относительно А, В, С: 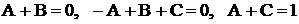 . Решив эту систему способом подстановки (или по формулам Крамера), получим
. Решив эту систему способом подстановки (или по формулам Крамера), получим 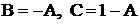 . Подставим эти значения во второе равенство:
. Подставим эти значения во второе равенство: 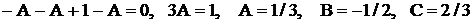 . Получаем разложение дроби
. Получаем разложение дроби 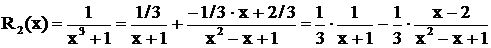 .
.
Замечание. Результат вычислений всегда можно проверить. Так, в последнем примере 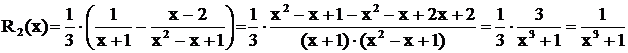 .
.
Упражнение. Разложить на простейшие дробь  . Разложив дробь
. Разложив дробь 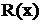 на простейшие и проинтегрировав полученное равенство, получим в правой части (в общем случае) сумму следующих четырех интегралов:
на простейшие и проинтегрировав полученное равенство, получим в правой части (в общем случае) сумму следующих четырех интегралов:

Первый из них по существу табличный: 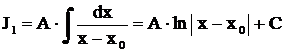 . Второй интеграл степенной:
. Второй интеграл степенной:
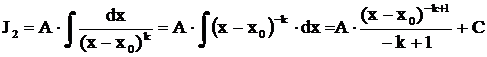 .
.
Третий интеграл был рассмотрен выше.
Рассмотрим подробнее интеграл 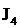 ,
, 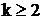 . Так как
. Так как 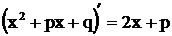 , чи-слитель представляем в виде
, чи-слитель представляем в виде 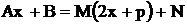 ,
,  . Интеграл
. Интеграл 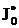 степенной, так как
степенной, так как
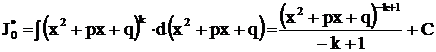 .
.
Для нахождения интеграла 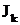 выделим из трехчлена полный квадрат:
выделим из трехчлена полный квадрат:
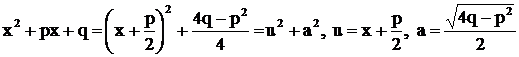 .
.
Тогда 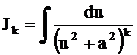 . Этот интеграл находится с помощью рекуррентного соотношения (15). Впрочем интеграл может быть найдем с помощью тригонометрической подстановки
. Этот интеграл находится с помощью рекуррентного соотношения (15). Впрочем интеграл может быть найдем с помощью тригонометрической подстановки  .
.
Пример. Найти интеграл  .
.
Решение. Так как 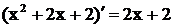 , получим
, получим 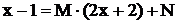 .
.
Тогда 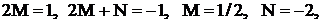
 .
.
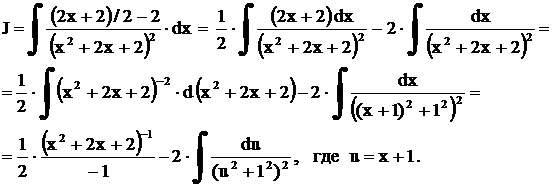
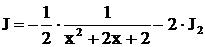 . Полагая в формуле (15)
. Полагая в формуле (15) 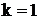 , получим
, получим
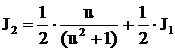 , где
, где 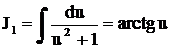 ,
,
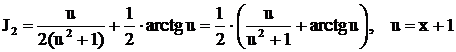 . Окончательно находим
. Окончательно находим

Для сравнения найдем 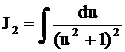 , где
, где 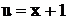 с помощью подстановки
с помощью подстановки 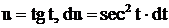 . Тогда
. Тогда  . Поэтому
. Поэтому
 . Так как
. Так как 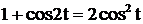 , получим
, получим
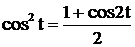 ,
, 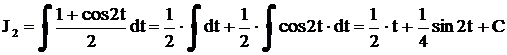 . Из подстановки следует, что
. Из подстановки следует, что 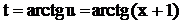 ,
,
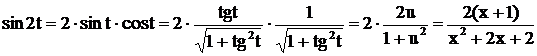 ,
,
 .
.
Решить примеры
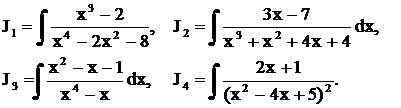 .
.
Решение.
 ,
,
 ,
,
 .
.
Интегралы вида  ,
,  , где m – целое положительное число, находятся с помощью тождеств
, где m – целое положительное число, находятся с помощью тождеств  ,
,  .
.
Пример. 

Пример. Найти интеграл 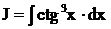 .
.
Решение. 
 .
.
Следующие три интеграла берутся с помощью известных формул тригонометрии  ,
,
 ,
,
 .
.
Пример. Найти интеграл  .
.
Решение. 
 ,
,  .
.
Подстановка  рекомендуется для нахождения интеграла
рекомендуется для нахождения интеграла  , а
, а
|
|
также в тех случаях, когда в интеграле  числа m и n - четные (положительные или отрицательные). Здесь используются известные формулы тригонометрии:
числа m и n - четные (положительные или отрицательные). Здесь используются известные формулы тригонометрии: 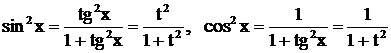 .
.
Пример. Найти интеграл 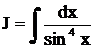 .
.
Решение.  ,
,
 ,
,
 . Так как
. Так как  , то окончательно
, то окончательно
получим  .
.
Замечание. Для интегралов  где k- натуральное число, методом интегрирования по частям можно получать рекуррентные соотношения, приведенные в таблице интегралов.
где k- натуральное число, методом интегрирования по частям можно получать рекуррентные соотношения, приведенные в таблице интегралов.
Решить самостоятельно

 ,
,  .
.
Выше были рассмотрены основные приемы и формулы для нахождения неопределенных интегралов. Следует отметить, что многие функции не интегрируются в конечном виде. Так, например, функция  непрерывна в промежутке
непрерывна в промежутке 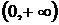 , однако, интеграл от нее
, однако, интеграл от нее  (интегральный синус) не выражается в конечном виде через элементарные функции. То же самое относится к
(интегральный синус) не выражается в конечном виде через элементарные функции. То же самое относится к
интегралам  (интегральный косинус),
(интегральный косинус),  (интегральный
(интегральный
логарифм).
Замечание. Во многих случаях заданный интеграл  может быть найден различными способами. Так, например, интеграл
может быть найден различными способами. Так, например, интеграл  с помощью подстановки
с помощью подстановки  дает
дает  , где
, где  ,
,  . С другой стороны, если возьмем подстановку
. С другой стороны, если возьмем подстановку 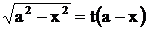 , то
, то  .
.
Поэтому  .
.
Окончательно  . Этот результат лишь формой отличается от предыдущего, так как
. Этот результат лишь формой отличается от предыдущего, так как
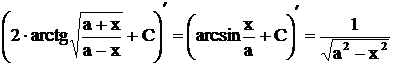 .
.
Две задачи математического анализа
Первая задача состоит в отыскании производной от заданной функции  . Напомним, что с помощью производной решаются многие задачи математики и физики. Так, например, если точка движется по закону
. Напомним, что с помощью производной решаются многие задачи математики и физики. Так, например, если точка движется по закону  , где t – время, а S – пройденный путь, то скорость движения
, где t – время, а S – пройденный путь, то скорость движения 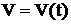 есть производная от пути по времени, т. е.
есть производная от пути по времени, т. е.  , а ускорение
, а ускорение  равно
равно  . Если масса неоднородного стержня изменяется по закону
. Если масса неоднородного стержня изменяется по закону  , то его плотность в точке х есть производная
, то его плотность в точке х есть производная 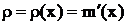 . В геометрии с помощью производной решается задача о проведении касательных к заданным кривым. Эти примеры можно продолжить.
. В геометрии с помощью производной решается задача о проведении касательных к заданным кривым. Эти примеры можно продолжить.
Теперь обратимся к обратной задаче: как по заданной производной  восстановить саму функцию
восстановить саму функцию  ?
?
Как, например, зная скорость движения 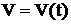 , найти закон изменения пройденного пути
, найти закон изменения пройденного пути  ? Как найти массу стержня переменной плотности
? Как найти массу стержня переменной плотности  ? В общем случае задача ставится следующим образом: пусть задана функция
? В общем случае задача ставится следующим образом: пусть задана функция  , производная от которой совпадает с заданной функцией:
, производная от которой совпадает с заданной функцией:  . Такая функция
. Такая функция  называется первообразной функции
называется первообразной функции  . Так, например, если
. Так, например, если  , то
, то  , так как
, так как  . Если
. Если  , то
, то  , так как
, так как 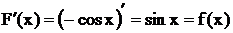 . Обратите внимание на то, что для заданной функции
. Обратите внимание на то, что для заданной функции  первообразных существует бесконечно много, так как
первообразных существует бесконечно много, так как  есть некоторая первообразная
есть некоторая первообразная  . Любая функция вида
. Любая функция вида  , где
, где  , есть также первообразная
, есть также первообразная  , так как
, так как  .
.
В силу этого множество всех первообразных заданной функции  принято обозначать символом
принято обозначать символом  и называть неопределенным интегралом от функции
и называть неопределенным интегралом от функции  . Итак, по определению,
. Итак, по определению,  .
.
Примеры.  , так как
, так как  .
.
 , так как
, так как  .
.
 , так как
, так как  .
.
Приступая к изучению неопределенного интеграла, следует обратить внимание на то, что
|
|
1) эта операция многозначная;
2) в техническом отношении интегрирование для студентов представляется более сложным, чем отыскание производных. Чтобы научиться интегрировать, нужна практика. Только решение большого числа разнообразных примеров позволит выработать некоторые навыки в интегрировании;
3) обратите внимание на запись интеграла. Здесь под знаком интеграла стоит дифференциал аргумента функции  . Если же задана сложная функция
. Если же задана сложная функция  , где
, где  , то все формулы интегрирования имеют смысл только в том случае, когда под знаком интеграла стоит дифференциал
, то все формулы интегрирования имеют смысл только в том случае, когда под знаком интеграла стоит дифференциал  . Это обстоятельство нужно иметь в виду постоянно. В формуле
. Это обстоятельство нужно иметь в виду постоянно. В формуле  будем подразумевать, что ищется интеграл от сложной функции
будем подразумевать, что ищется интеграл от сложной функции 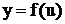 , где
, где  , х – независимая переменная;
, х – независимая переменная;
4) существуют шесть тригонометрических функций: 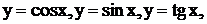
 . Последние две функции определяются как величины, обратные по отношению к
. Последние две функции определяются как величины, обратные по отношению к  , т. е.
, т. е. 
 .
.
Это позволяет известные формулы тригонометрии
 записывать в целом виде:
записывать в целом виде:
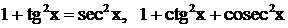 .
.
Таблицы производных и интегралов поэтому имеют более простой вид. При интегрировании гиперболических функций  ,
,  ,
,  ,
,  следует помнить основные формулы, связывающие их:
следует помнить основные формулы, связывающие их:  , а также формулы понижения
, а также формулы понижения  ;
;
5) поскольку операции дифференцирования и интегрирования тесно связаны, ниже приводятся основные свойства производной и формулы дифференцирования, а далее – аналогичный материал, касающийся неопределенного интеграла.
|
|
|

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!