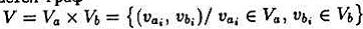Билет №4:Функции. Операция.
Подмножество F⊂My*Mx называется функцией, если для одного элемента x∈Mx найдется не более одного элемента y∈My, вида (х,у) ∈F, при этом функция называется всюду (полностью =) определенной; в противном случае функция называется частично определенной(неопределенной)
Множество Мх образует область определения функции F, множество Му – область значений функции F.
Кол-во аргументов определяет местность функции.
n-местная функция – когда множество Мх в определении функции у = F(x) яв-ся декартовым произведением множеств Mx1, Mx2,…,Mxn,
y = F(x1,x2,..,xn)
Частичный случай n-местной функции y = F(x1,x2,xn) является n-местной операцией.
n-местнойоперациейOn в множестве М понимается n-местная функция y = F(x1,x2,..,xn), у которой области определения аргументов и область значений функции совпадает
M = Mx1 = Mx2 = …=Mxn = My
Таким образом, n-местная операция по n-элементам множества M определяет (n+1)- й элемент этого же множества.
Имеются 4 операции над множествами(3 билет)
Операции над множествами:
1) Объединение Ma∪Mb двух множеств Ma и Mb является множество M1 состоящее из элементов множества Ma и из элементов множества Mb
M=Ma∪Mb={mi/mi∈Ma и mi∈Mb}
2) Пересечением Ma∩Mb двух множеств Ma и Mb является множество M1 состоящее из элементов, которые принадлежат как множеству Ma, так и множеству Mb:
M=Ma∩Mb={mj/mj∈Ma и mi∈Mb}
3) Разностью Ma/Mbдвух множеств Ma иMb является множество M1 состоящее из элементов, которые принадлежат множеству Ma, и не принадлежащих множеству Mb:
M=Ma/Mb={mj/mj∈Ma и mi∉Mb}
Эти операции являются двуместными.
4) Операция "Дополнения" является одномерной. Дополнением M множества M является множество:
M={mj/mj∉M}
Множество можно задать выражением, в которое входят идентификаторы (указатели) множеств, операции и, быть может, скобки. такой способ задания называется аналитическим.
5)Фундаментальные алгебры
Алгебра А - совокупность множества М с заданными в нем операциями
S={f11,f12,…,f1n1,f21,f22,…,f2n2,…,fm1,fm2,…,fmnm} (обозначается А=<M,S>), где первый индекс идентификатора операции указывает на размерность.
Рассмотрим фундаментальные алгебры.
Алгебра вида <M,f2> -группоид. Если f2 –операция типа умножения, то группоид мультипликативный, если f2 – операция типа сложения, то группоид аддитивный.
Пусть А=<M,f2> - группоид. Обозначим f2 как о, тогда элемент е, принадлежащий М, называется правым нейтральным элементом группоида А, если для любого м, принадлежащего М, выполняется м о е = м, и левым нейтральным элементом группоида А, если е о м = м.
Если е, принадлежащий М, группоида А=<M,o> - и левый, и правый нейтральный элемент группоида А, то его называют двустронним нейтральным элементом (или нейтральным элементом). Никакой группоид не может иметь более одного нейтрального элемента. Если группоид А=<M,o> мультипликативный, то нейтральный элемент называется единицей и обозначается 1. Если группоид аддитивный, то нейтральный элемент – нуль и обозначается 0.
Группоид А – иденпотентный, если его сигнатура удовлетворяет закону иденпотентности: для любого м, принадлежащего М, выполняется м о м = м.
Группоид А – коммутативный (абелевый), если его сигнатура удовлетворяет закону коммутативности:: для любых х и у, принадлежащих М, выполняется х о у = у о х.
Группоид А – ассоциативный (полугруппа), если его сигнатура удовлетворяет закону ассоциативности:: для любых х, у и z, принадлежащих М, выполняется
х о (у о z) = (х о у) о z.
Полугруппа <М,о>, в которой обратные операции(то есть для любых а и b, принадлежащих М, каждое из уравнений а о х = b, у о а = b) обладают единственным решением, называется группой.
Алгебра <М,*,+>, в которой умножение связано со сложением законами дистрибутивности (а*(b+с)=а*b+b*с, (b+с)*a=b*а+с*а), называется кольцом.
Кольцо, в котором все отличные от нуля элементы составляют группу по уножению, называется телом. Тело, у которого мультипликативная группа абелева, называется полем.
Билет №6:Алгебра Кантора, Законы алгебры Кантора.
Алгебра множеств (алгебра Кантора, алгебра классов)
Ак=<B(1), ∪,∩, ->, носителем которой является булеан универсального множества 1, сигнатурой- операции объединения U, пересечения ∩ и дополнения
Законы алгебры Кантора
1) Закон коммуникативности, объединения и пересечения:
Ma∪Mв=Мв∪Ма, Ма∩Мв = Мв∩Ма;
2) Закон ассоциативности, объединения и пересечения
Ma∪(Мв∪Мс) = (Ma∪Mв)∪Мс;
Ma∪(Мв∩Мс) = (Ma∩Mв) ∩Мс;
3) Закон дистрибутивности, пересечения относительно объединения и объединения относительно пересечения:
Ма ∩(Мв∪Мс) = Ма∩Мв∪Ма∩Мс;
Ma∪Мв∩Мс = (Ma∪Mв) ∩ (Ма∪Мс);
4) Законпоглощения:
Ма∪Ма∩Мв = Ма, Ма ∩(Ма∪Мв)= Ма;
5) Законсохранения
Ма∩Мв∪Ма∩ 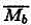 = Ма,
= Ма,
(Ма∪Мв) ∩(Ма∪ 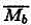 ) = Ма;
) = Ма;
6) ЗаконыПорецкого
Ма∪ 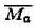 ∩Мв = Ма∪Мв;
∩Мв = Ма∪Мв;
Ма∩(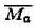 ∪Мв) = Ма∩Мв;
∪Мв) = Ма∩Мв;
7) Закон идемпотентности объединения и пересечения
Ма∪Ма = Ма
Ма∩Ма=Ма
8) Закон действия с универсальным (1) и пустым множествами:
М∪ 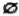 = М, М∩
= М, М∩ 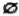 =
= 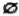 , М∪1 = 1;
, М∪1 = 1;
М∩1 = М, М∪ 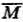 = 1, М∩
= 1, М∩ 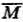 =
= 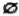 ;
;
9) Закон де Моргана
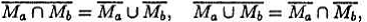
10) Закон двойного дополнения
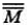 = М.
= М.
7)Граф. Способы задания графа.
Граф G – совокупность множества М с заданным бинарным отношением Т, G=<M,T>.
Граф G – совокупность множества вершин и множества дуг. G=<V,U>
Способы здания:
1)Теоретико-множественный: граф описывается перечислением множества вершин и дуг.
2)Графический(?)
3)Матричный:
I тип – матрица инцеденций. Если граф G содержит n вершин и m дуг, то матрица инцеденций – A(G)=[aij]m*n, где aij=1(если вершина vj – начало дуги ui), -1 (если вершина vj – конец дуги ui) или 0(если вершина vj не коинцедентна дуге ui).
Но эта матрица не подходит для графов с петлями. Для этого применяются А+ и А- , где А+ -начальная, а А- конечная матрица инцеденций.
А+ (G)=[a+ij]m*n, где a+ij=1 (если вершина vj – начало дуги ui) или 0(в противном случае).
А- (G)=[a-ij]m*n, где a-ij=1 (если вершина vj – конец дуги ui) или 0(в противном случае).
II тип – матрица смежности S.
S=[sij]n*n, где sij= 1 (если ребро (vi,vj) принадлежит U) и 0 (в противном случае).
Билет №9: Связность графа
Граф G<V,U> наз-ся связным, если любая его вершина соединена цепью.
Компонент связности – максимальный по включению вершин связный подграф графа.
Граф наз-ся несвязным, если число его компонент больше одной.
Алгоритмсвязанности графа и числа его компонент:
Теорема: Элемент матрицы Sn, где S=[Sij]-матрица смежности, Sijесть множество последовательных идентификаторов ребер, образующих цепь между Uiи Uj, представляет собой множество цепей длины и, соединяющих вершины Uiи Uj.
При возведении в n-го степень матрицы смежности S=[ Sij] умножение рассматривается, как конкатенация (справа к идентификатору, соответствующему i-й строке, идентификатора, соответствующему j-му столбцу)
Расстояние r(Ui, Uj) – это минимальная длина цепи, соединяющей вершины Uiи Uj: r(Ui, Uj) = maxminLk(Ui, Uj).
Метрика – введенная на множество всех вершин (Ui, Uj) графа G функция r(Ui, Uj)
Условие связности:
D (G) =ΣM(G)i=1[S]I
Алгоритм определения связности графа.
Возводим матрицу S В n-ую степень
Здесь в матрице SnSIJ- пути из Viв Vj длиной n.
2. Если в матрице d’ нет нулевых элементов граф является связным (к=1), d(G)- диаметр графа - кратчайший путь между вершинами.
3.связность графа (X(G)) наименьшее число вершин, удаление которых делает граф несвязным.
Если X(G)=n, то граф называется n-связным.
Рёберная связность (M(G))- наименьшее количество рёбер, удаление которых делает граф несвязным.
Разрез графа – множество рёбер, при удалении которых связанный граф перестает быть связным, а при добавлении в это множество хотя одного ребра, не вошедшего в это множество граф, становится связным.
Х - поциклический рост - число ребер в остовном лесе графа:
Х(G)=|V|- k
Дерево - связный граф, не содержащий циклов.
Остовной подграф - подграф, содержащий все вершины графа.
Остов - остовной подграф являющийся деревом.
Остовной лес- граф, каждая компонента которого связности которого является остовным деревом.
Сильная связность графа.
Граф G = <V,U> называется сильно связным, если любая пара вершин соединена путем.
Максимальной по включению вершин сильно связанный подграф графа называется его компонентой сильной связности.
Граф называется несильно связанным, если число его компонент сильной связности больше 1.
Цикломатика
Для исследования циклов в графе используют цикломатическую матрицу C(G)=[cij]: каждому циклу графа взаимно однозначно сопоставляется вектор-строка матрицы C(G); каждый элемент этой строки определяется как
1, если j-е ребро входит в i-й цикл,
0 в противном случае.
Базисом векторного пространства называются всякая система линейно независимых векторов, порождающая данное пространство. Любой вектор графа G может быть представлен в виде комбинации векторов базиса циклов.
Деревом называется связный граф, не содержащий ни одного цикла.
Остовный подграф графа – это подграф, содержащий все вершины графа.
Остовом называются остовный подграф являющийся деревом.
Хордой остова D в связном графе G называется всякое ребро графа, не принадлежащие D. Любой подграф состоящий из хорды и остова, имеет точно один цикл.
Цикломатическое число v(G) графа G равно числу хорд любого остова в G. Если связанный граф G имеет n вершин и m ребер, то v(G) = m – n + 1. Если граф G содержит k компонент связанности, то если цикломатическое число есть v(G) = m – n + k. Цикломатическое число определяет меру связности графа.
Лесом называется граф, не содержащий циклов. Иными словами, если граф состоит из нескольких компонент связности, каждая из которых является деревом, то данный граф является лесом.
Остовным лесом называется граф, каждая компонента которого является остовным деревом.
Цикломатический ранг x(G) (ранг разреза) – это число ребер в его остовном лесе. Количество базисных циклов в графе G определяется цикломатическим числом графа v(G).
Теорема №1 (Эйлер)
Число базисных циклов графа постоянно и равно его цикломатическому числу.
Часто матрицу инциденции А и цикломатическую матрицу С называют первой матрицей инциденций и второй матрицей инциденций.
Теорема №2
Вторая и первая матрица инциденций линейного графа G связаны операцией матричного умножения: C(G) xA(G) = 0(mod 2).
Базисная система разрезов образует базис в пространстве разрезов, или пространстве коциклов. Эта система может быть записана в виде соответствующей базисной матрицы разрезов, или базисной коцикломатической матрицы (хорды справа).
Теорема №3
Граф является двудольным тогда и только тогда, когда все его циклы имеют четную длину (четны).
В двудольном графе не обязательно каждая вершина из V1 соединена с каждой вершиной из V2, но если это так, то граф называется полным двудольным графом и обозначается Km,n, где m – число вершин V1, а n – число вершин V2. Полный двудольный граф называется звездным графом (звездой, граф Кёнинга) и является деревом.
Коцикломатика
Коцикломатика (если спросят) – нахождение разрезов графа.
Разделяющим множеством связного графа называется такое множество его ребер, удаление которых из графа делает его несвязным.
Разрезом называется такое разделяющее мн-во, которое не имеет собственного разделяющего подмножества(коцикл).
Лес – граф, не содержащий циклов, т.е. если граф состоит из нескольких компонент связности, каждая из которых является деревом, то данный подграф является лесом.
Коциклический ранг χ(G) (ранг разреза) – это число ребер в его остовном лесе: χ(G) = n-k (n – кол-во вершин, k – количество компонент связности)
Теорема Эйлера: Число базисных циклов графа постоянно и равно его цикломатическому числу.
Алгоритм нахождения разрезов:
1) рисуем остов.
2) строим коцикломатическую таблицу (это когда сначала указываются ребра остова, а потом хорды)
3) по диагонали (в ребрах) выставляем единицы – базис. Дальше логика такая:
Удаляется ребро остова. Множество вершин при этом распадается на два непересекающихся подмножества V1 и V2. Множество всех ребер графа, каждое из которых соединяет вершину из V1 с вершиной из V2, является разрезом графа. Множество всех разрезов для каждого ребра остова является базисной системой разрезов для данного остова.
4) путем сложения разрезов из базиса (2χ - χ -1 раз) порождаем все подмножество коциклов(разрезов) графа.
Дифференцирование графов.
Продифференцировать граф G по событию S – построить производную графа G по событию S.
Событие – процесс, происходящий при выполнении определенных условий.
Каждое событие определяет матрицу инцедентности Q, столбцами которой являются условия, а строками – события. Q=[qij]=1(если условие участвует в образования события) или 0 (иначе).
Чтобы продифференцировать граф по событию S, нужно:
1)Построить модель, определяемую заданным событием.
2)Построить частотную матрицу отношений F=[fij]n*n –матрицу, каждой строке(столбцу) которой взаимно однозначно соответствует условие и элемент fij, равный числу событий, в котором входят условия i и j (если i не равен j, иначе (при i=j) fij равен числу событий, в которых участвует условие i). При этом, если i=j, то fi – собственная частота условия, а если i<>j, то fij – взаимная частота условий i и j. Частотная матрица отношений F симметрична относительно главной диагонали.
F=QT*Q.
3)Построить производную графа G по событию S- неориентированный взвешенный граф <V,(U,P)>, носитель которого совпадает с носителем модели, определяемой этим событием, и пара вершин (vi,vj) взвешена отношением частоты их несовместного участия к частоте совместного участия в событии S.
 - значение производной на ребре
- значение производной на ребре
(vi,vj).
Раскраска вершин
Раскрасить вершины графа значит сопоставить каждой вершине графа идентификатор краски таким образом, чтобы кол-во этих красок было минимальным и 2 любые вершины, покрашенные одной краской, не были бы смежные. Если по-простому, то раскраской вершин графа называется назначение цветов его вершинам. Обычно цвета - это числа 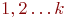 (также можно использовать латинские буквы). Тогда раскраска является функцией, определенной на множестве вершин графа и принимающей значения в множестве
(также можно использовать латинские буквы). Тогда раскраска является функцией, определенной на множестве вершин графа и принимающей значения в множестве  . Раскраску можно также рассматривать как разбиение множества вершин
. Раскраску можно также рассматривать как разбиение множества вершин 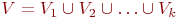 , где
, где 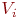 - множество вершин цвета
- множество вершин цвета  . Множества
. Множества 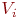 называют цветными классами. Раскраска называется правильной, если каждый цветной класс является независимым множеством. Иначе говоря, в правильной раскраске любые две смежные вершины должны иметь разные цвета. Задача о раскраске состоит в нахождении правильной раскраски данного графа
называют цветными классами. Раскраска называется правильной, если каждый цветной класс является независимым множеством. Иначе говоря, в правильной раскраске любые две смежные вершины должны иметь разные цвета. Задача о раскраске состоит в нахождении правильной раскраски данного графа  в наименьшее число цветов. Это число называется хроматическим числом графа и обозначается
в наименьшее число цветов. Это число называется хроматическим числом графа и обозначается 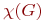 .
.
В правильной раскраске полного графа 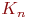 все вершины должны иметь разные цвета, поэтому
все вершины должны иметь разные цвета, поэтому 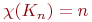 . Если в каком-нибудь графе имеется полный подграф с
. Если в каком-нибудь графе имеется полный подграф с 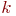 вершинами, то для раскраски этого подграфа необходимо
вершинами, то для раскраски этого подграфа необходимо 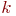 цветов. Отсюда следует, что для любого графа выполняется неравенство
цветов. Отсюда следует, что для любого графа выполняется неравенство
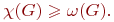
Однако хроматическое число может быть и строго больше кликового числа. (Клика — подмножество вершин графа, полностью соединённых друг с другом, то есть подграф, являющийся полным графом. Кликовое число — число (G) вершин в наибольшей клике. Другие названия — густота, плотность. Максимальная клика — клика с максимально возможным числом вершин среди клик графа.)
Внешняя устойчивость графа
Гиперкуб
Гиперкуб – это математическая модель дискретного пространства.
Гиперкуб – это граф, носитель которого соответствует точкам математического пространства, и две вершины смежны в том случае, если соответствующие им точки пространства имеют общую границу, т.е. расстояние по Хэммингу между координатами этих точек =1.
Иначе говоря, гиперкуб – это математическая модель дискретного пространства размерности n, представляющая собой граф, носителем которого являются вершины, каждая из которых соответствует точке пространства, и два вершины соединяются ребром, если между точками, соответствующими этим вершинам, есть различие и только в одном разряде. Мощность его носителя равна 2n, мощность сигнатуры равна n*2n-1.
Для булевого пространства, т.е. пространства, в котором каждая координата может принимать значение 0 или 1, расстояние по Хэммингу равно количеству различных координат (различных разрядов в координатах).
Свойства гиперкуба, вытекающие из ярусной упорядоченности вершин гиперкуба:
Если вершины в гиперкубе упорядочены по ярусам таким образом, что в одном ярусе сгруппированы вершины, в кодах которых одинаковое количество нулей или единиц, то:
1)количество ярусов = n+1, где n – размерность гиперкуба.
2) количество вершин в каждом ярусе  , n – размерность, k - значность
, n – размерность, k - значность
3) вершины в ярусе смежны только с вершинами из верхнего яруса или из нижнего яруса.
+
4) степень вершины гиперкуба размерности n равна n.
5) размерность n содержит 2nвершин
3) H=2 для любого гиперкуба с k=2 (если значность k гиперкуба равна 2, то хроматическое число H равно 2.
Гиперкубы находят применение в теории кодирования при передаче данных и при проектировании автоматов.
Вложение графа в гиперкуб
Большой практический интерес представляет проблема вложения графов в другие графы, имеющие специальные структурные свойства. Важным классом таких графов является класс n-мерных кубов. Они находят применение в теории кодирования при передаче данных и при проектировании автоматов. Обозначим n-мерный куб через Hn. Мощность его носителя равна 2n, мощность сигнатуры – n*2n-1. Множество вершин n-куба вместе с введенной таким образом метрикой, является метрическим пространством, которое назовем булевым пространством. Граф  называется вложимым в булево пространство Нn<VH,UH> или кубируемым, если существует соответствие ϕ между вершинами графа G и гиперкуба Hnтакое, что если (
называется вложимым в булево пространство Нn<VH,UH> или кубируемым, если существует соответствие ϕ между вершинами графа G и гиперкуба Hnтакое, что если ( .Так как n-куб является двудольным графом, то в соответствии с теоремой Кёнига все его простые циклы четны, и поэтому любой граф, который содержит подграф, являющийся нечетным циклом, некубируем. Следовательно циклы нечетной длины и граф Кёнига К2,3
.Так как n-куб является двудольным графом, то в соответствии с теоремой Кёнига все его простые циклы четны, и поэтому любой граф, который содержит подграф, являющийся нечетным циклом, некубируем. Следовательно циклы нечетной длины и граф Кёнига К2,3  являются запрещенными фигурами вложения графа в булево пространство. Под запрещенной фигурой в данном случае понимаем критически невложимый граф, т.е. некубируемый граф, у которого все частичные графы кубируемые.
являются запрещенными фигурами вложения графа в булево пространство. Под запрещенной фигурой в данном случае понимаем критически невложимый граф, т.е. некубируемый граф, у которого все частичные графы кубируемые. 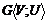 ;
;  называется изоморфным если существует такое взаимно однозначное соответствие между вершинами V и V’, что вершины Va и Vв соединены дугой (Va,Vв) в одном из графов в том и только в том случае когда соответствующие им вершины V’a и V’в соединены дугой (V’a,V’в) в другом графе.
называется изоморфным если существует такое взаимно однозначное соответствие между вершинами V и V’, что вершины Va и Vв соединены дугой (Va,Vв) в одном из графов в том и только в том случае когда соответствующие им вершины V’a и V’в соединены дугой (V’a,V’в) в другом графе.  граф G изоморфен графу G’. Два графа гомеоморфные если они изоморфны с точностью степени два. Вложить граф в гиперкуб это значит установить изоморфизм между графом и гиперкубом. Гиперкубом – называется граф каждая вершина которого соответствует области пространства, и две вершины соединены ребром если они соответствуют соседним областям имеющих общую границу. Размерность пространства- размерность гиперкуба, n-значность логики.
граф G изоморфен графу G’. Два графа гомеоморфные если они изоморфны с точностью степени два. Вложить граф в гиперкуб это значит установить изоморфизм между графом и гиперкубом. Гиперкубом – называется граф каждая вершина которого соответствует области пространства, и две вершины соединены ребром если они соответствуют соседним областям имеющих общую границу. Размерность пространства- размерность гиперкуба, n-значность логики.
Алгоритм вложения графа в гиперкуб.
1)устраняем запрещенные фигуры – структура в графе мешающая решению поставленной задачи-циклы нечетной длины, запрещенные фигуры при вложении графа в гиперкуб. Удаление запрещенных фигур осуществляется путем навешивания дополнительных вершин на соответствующие ребра.
2)Устанавливаем размерность а)maxS(V1); в) ] log2|V| [; из а и в выбираем мах- это и будет размерность гиперкуба: n = max(maxS(V1), ] log2|V| [)
3)Ярусно упорядочиваем граф начиная с вершины с мах
степенью устанавливаем изоморфизм между графом и гиперкубом размерности n. При необходимости размерность куба может быть увеличена.
Если при установке изоморфизма невозможно установить соответствие между какой-либо вершиной графа и вершиной гиперкуба из-за топологических свойств, можно удалить какое-либо ребро графа путем навешивания 2-х дополнительных вершин на это ребро.
Планарный граф. Вложение графа в плоскость
Планарный граф — граф, который может быть изображен на плоскости без пересечения ребер. Граф укладывается на некоторой поверхности, если его можно на ней нарисовать без пересечения ребер. Уложенный граф называется геометрическим, его вершины — это точки плоскости, а ребра — линии на ней. Области, на которые граф разбивает поверхность, называются гранями. Плоский граф — граф, уложенный на плоскость. Граф называется планарным, если он изоморфен некоторому плоскому графу
*я незнаю нужно ли это или нет
Топология исследует свойства графов, инвариантные относительно гомеоморфных преобразований. Эти свойства определяются топологическими инвариантами. Два графа гомеоморфны, если они изоморфны с точностью до вершин степени 2. Другими словами, два графа гомеоморфны, если они преобразуются до графов, изоморфных друг другу, заменой некоторых ребер цепями соответствующей длины. Род поверхности – это наибольшее число простых замкнутых кривых на поверхности, которые не разъединяют эту поверхность. Сфера и плоскость являются поверхностями нулевого рода, поскольку их разъединяет любая замкнутая прямая. Тор поверхность первого рода. Любая поверхность p-го рода эквивалентна сфере с p ручками.
Граф называется планарным, если он изображается на плоскости так, что его ребра пересекаются только в вершинах. Теорема: Граф планарен тогда и только тогда, когда он не содержит подграфа, гомеоморфного F5 или К3,3 или графов стягиваемых к F5 или к К3,3. Толщиной графа G называется наименьшее число планарных графов, объединение которых дает G. Толщина планарного графа равна 1. Нижняя оценка толщины t(G) графа  определяется неравенством
определяется неравенством  , где ] [ -целая часть, |V|=n, si- степень i –ой вершины. Чтобы определить, какие ребра необходимо удалить для преобразования графа в планарный, выделим все запрещенные фигуры и построим двумерную таблицу, каждая строка которой взаимно однозначно соответствует запрещенной фигуре Qi, a столбец – ребру Pi. тогда покрытие строк столбцами этой таблицы определит, какие ребра необходимо удалить, чтобы граф стал планарным. Минимальное покрытие будет соответствовать минимальному решению, так как удаление любого ребра выводит запрещенную фигуру из класса подграфов, гомеоморфных F5 или К3,3.
, где ] [ -целая часть, |V|=n, si- степень i –ой вершины. Чтобы определить, какие ребра необходимо удалить для преобразования графа в планарный, выделим все запрещенные фигуры и построим двумерную таблицу, каждая строка которой взаимно однозначно соответствует запрещенной фигуре Qi, a столбец – ребру Pi. тогда покрытие строк столбцами этой таблицы определит, какие ребра необходимо удалить, чтобы граф стал планарным. Минимальное покрытие будет соответствовать минимальному решению, так как удаление любого ребра выводит запрещенную фигуру из класса подграфов, гомеоморфных F5 или К3,3.
Билет №4:Функции. Операция.
Подмножество F⊂My*Mx называется функцией, если для одного элемента x∈Mx найдется не более одного элемента y∈My, вида (х,у) ∈F, при этом функция называется всюду (полностью =) определенной; в противном случае функция называется частично определенной(неопределенной)
Множество Мх образует область определения функции F, множество Му – область значений функции F.
Кол-во аргументов определяет местность функции.
n-местная функция – когда множество Мх в определении функции у = F(x) яв-ся декартовым произведением множеств Mx1, Mx2,…,Mxn,
y = F(x1,x2,..,xn)
Частичный случай n-местной функции y = F(x1,x2,xn) является n-местной операцией.
n-местнойоперациейOn в множестве М понимается n-местная функция y = F(x1,x2,..,xn), у которой области определения аргументов и область значений функции совпадает
M = Mx1 = Mx2 = …=Mxn = My
Таким образом, n-местная операция по n-элементам множества M определяет (n+1)- й элемент этого же множества.
Имеются 4 операции над множествами(3 билет)
Операции над множествами:
1) Объединение Ma∪Mb двух множеств Ma и Mb является множество M1 состоящее из элементов множества Ma и из элементов множества Mb
M=Ma∪Mb={mi/mi∈Ma и mi∈Mb}
2) Пересечением Ma∩Mb двух множеств Ma и Mb является множество M1 состоящее из элементов, которые принадлежат как множеству Ma, так и множеству Mb:
M=Ma∩Mb={mj/mj∈Ma и mi∈Mb}
3) Разностью Ma/Mbдвух множеств Ma иMb является множество M1 состоящее из элементов, которые принадлежат множеству Ma, и не принадлежащих множеству Mb:
M=Ma/Mb={mj/mj∈Ma и mi∉Mb}
Эти операции являются двуместными.
4) Операция "Дополнения" является одномерной. Дополнением M множества M является множество:
M={mj/mj∉M}
Множество можно задать выражением, в которое входят идентификаторы (указатели) множеств, операции и, быть может, скобки. такой способ задания называется аналитическим.
5)Фундаментальные алгебры
Алгебра А - совокупность множества М с заданными в нем операциями
S={f11,f12,…,f1n1,f21,f22,…,f2n2,…,fm1,fm2,…,fmnm} (обозначается А=<M,S>), где первый индекс идентификатора операции указывает на размерность.
Рассмотрим фундаментальные алгебры.
Алгебра вида <M,f2> -группоид. Если f2 –операция типа умножения, то группоид мультипликативный, если f2 – операция типа сложения, то группоид аддитивный.
Пусть А=<M,f2> - группоид. Обозначим f2 как о, тогда элемент е, принадлежащий М, называется правым нейтральным элементом группоида А, если для любого м, принадлежащего М, выполняется м о е = м, и левым нейтральным элементом группоида А, если е о м = м.
Если е, принадлежащий М, группоида А=<M,o> - и левый, и правый нейтральный элемент группоида А, то его называют двустронним нейтральным элементом (или нейтральным элементом). Никакой группоид не может иметь более одного нейтрального элемента. Если группоид А=<M,o> мультипликативный, то нейтральный элемент называется единицей и обозначается 1. Если группоид аддитивный, то нейтральный элемент – нуль и обозначается 0.
Группоид А – иденпотентный, если его сигнатура удовлетворяет закону иденпотентности: для любого м, принадлежащего М, выполняется м о м = м.
Группоид А – коммутативный (абелевый), если его сигнатура удовлетворяет закону коммутативности:: для любых х и у, принадлежащих М, выполняется х о у = у о х.
Группоид А – ассоциативный (полугруппа), если его сигнатура удовлетворяет закону ассоциативности:: для любых х, у и z, принадлежащих М, выполняется
х о (у о z) = (х о у) о z.
Полугруппа <М,о>, в которой обратные операции(то есть для любых а и b, принадлежащих М, каждое из уравнений а о х = b, у о а = b) обладают единственным решением, называется группой.
Алгебра <М,*,+>, в которой умножение связано со сложением законами дистрибутивности (а*(b+с)=а*b+b*с, (b+с)*a=b*а+с*а), называется кольцом.
Кольцо, в котором все отличные от нуля элементы составляют группу по уножению, называется телом. Тело, у которого мультипликативная группа абелева, называется полем.
Билет №6:Алгебра Кантора, Законы алгебры Кантора.
Алгебра множеств (алгебра Кантора, алгебра классов)
Ак=<B(1), ∪,∩, ->, носителем которой является булеан универсального множества 1, сигнатурой- операции объединения U, пересечения ∩ и дополнения
Законы алгебры Кантора
1) Закон коммуникативности, объединения и пересечения:
Ma∪Mв=Мв∪Ма, Ма∩Мв = Мв∩Ма;
2) Закон ассоциативности, объединения и пересечения
Ma∪(Мв∪Мс) = (Ma∪Mв)∪Мс;
Ma∪(Мв∩Мс) = (Ma∩Mв) ∩Мс;
3) Закон дистрибутивности, пересечения относительно объединения и объединения относительно пересечения:
Ма ∩(Мв∪Мс) = Ма∩Мв∪Ма∩Мс;
Ma∪Мв∩Мс = (Ma∪Mв) ∩ (Ма∪Мс);
4) Законпоглощения:
Ма∪Ма∩Мв = Ма, Ма ∩(Ма∪Мв)= Ма;
5) Законсохранения
Ма∩Мв∪Ма∩ 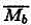 = Ма,
= Ма,
(Ма∪Мв) ∩(Ма∪ 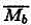 ) = Ма;
) = Ма;
6) ЗаконыПорецкого
Ма∪ 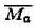 ∩Мв = Ма∪Мв;
∩Мв = Ма∪Мв;
Ма∩(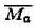 ∪Мв) = Ма∩Мв;
∪Мв) = Ма∩Мв;
7) Закон идемпотентности объединения и пересечения
Ма∪Ма = Ма
Ма∩Ма=Ма
8) Закон действия с универсальным (1) и пустым множествами:
М∪ 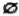 = М, М∩
= М, М∩ 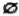 =
= 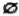 , М∪1 = 1;
, М∪1 = 1;
М∩1 = М, М∪ 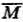 = 1, М∩
= 1, М∩ 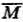 =
= 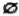 ;
;
9) Закон де Моргана
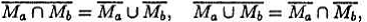
10) Закон двойного дополнения
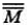 = М.
= М.
7)Граф. Способы задания графа.
Граф G – совокупность множества М с заданным бинарным отношением Т, G=<M,T>.
Граф G – совокупность множества вершин и множества дуг. G=<V,U>
Способы здания:
1)Теоретико-множественный: граф описывается перечислением множества вершин и дуг.
2)Графический(?)
3)Матричный:
I тип – матрица инцеденций. Если граф G содержит n вершин и m дуг, то матрица инцеденций – A(G)=[aij]m*n, где aij=1(если вершина vj – начало дуги ui), -1 (если вершина vj – конец дуги ui) или 0(если вершина vj не коинцедентна дуге ui).
Но эта матрица не подходит для графов с петлями. Для этого применяются А+ и А- , где А+ -начальная, а А- конечная матрица инцеденций.
А+ (G)=[a+ij]m*n, где a+ij=1 (если вершина vj – начало дуги ui) или 0(в противном случае).
А- (G)=[a-ij]m*n, где a-ij=1 (если вершина vj – конец дуги ui) или 0(в противном случае).
II тип – матрица смежности S.
S=[sij]n*n, где sij= 1 (если ребро (vi,vj) принадлежит U) и 0 (в противном случае).
Билет №8: Операции над множествами
Для представления графов в виде композиции более простых графов существует 3 операции:
1) Объединение графов: Ga=<Va,Ua>b и Gв=<Vв,Uв> называется граф G<V,U>, носитель и сигнатура которого является соответственно теоретико- множественным объединением носителей Va и сигнатур Ua, Uв графов Ga, Gв.
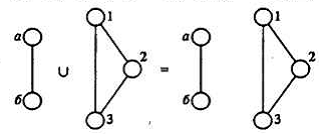
2) Суммой графов Ga=<Va,Ua>b и Gв=<Vв,Uв> называется граф G<V,U>, представляющий собой объединение графов Ga, Gв и двудольного полного графа 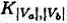 , построенного на носителях
, построенного на носителях
Va\Va∩Vв и Vв\Va∩Vв

3) Декартовое произведение графов Ga=<Va,Гa>b и Gв=<Vb,Гb> называется граф G<V,Г>,
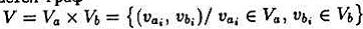
Г(Uai,Uвi) = Гuai х Гuвi
Билет №9: Связность графа
Граф G<V,U> наз-ся связным, если любая его вершина соединена цепью.
Компонент связности – максимальный по включению вершин связный подграф графа.
Граф наз-ся несвязным, если число его компонент больше одной.
Алгоритмсвязанности графа и числа его компонент:
Теорема: Элемент матрицы Sn, где S=[Sij]-матрица смежности, Sijесть множество последовательных идентификаторов ребер, образующих цепь между Uiи Uj, представляет собой множество цепей длины и, соединяющих вершины Uiи Uj.
При возведении в n-го степень матрицы смежности S=[ Sij] умножение рассматривается, как конкатенация (справа к идентификатору, соответствующему i-й строке, идентификатора, соответствующему j-му столбцу)
Расстояние r(Ui, Uj) – это минимальная длина цепи, соединяющей вершины Uiи Uj: r(Ui, Uj) = maxminLk(Ui, Uj).
Метрика – введенная на множество всех вершин (Ui, Uj) графа G функция r(Ui, Uj)
Условие связности:
D (G) =ΣM(G)i=1[S]I
Алгоритм определения связности графа.
Возводим матрицу S В n-ую степень
Здесь в матрице SnSIJ- пути из Viв Vj длиной n.
2. Если в матрице d’ нет нулевых элементов граф является связным (к=1), d(G)- диаметр графа - кратчайший путь между вершинами.
3.связность графа (X(G)) наименьшее число вершин, удаление которых делает граф несвязным.
Если X(G)=n, то граф называется n-связным.
Рёберная связность (M(G))- наименьшее количество рёбер, удаление которых делает граф несвязным.
Разрез графа – множество рёбер, при удалении которых связанный граф перестает быть связным, а при добавлении в это множество хотя одного ребра, не вошедшего в это множество



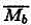 = Ма,
= Ма,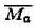 ∩Мв = Ма∪Мв;
∩Мв = Ма∪Мв;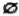 = М, М∩
= М, М∩ 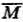 = 1, М∩
= 1, М∩ 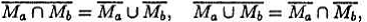
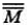 = М.
= М. - значение производной на ребре
- значение производной на ребре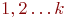 (также можно использовать латинские буквы). Тогда раскраска является функцией, определенной на множестве вершин графа и принимающей значения в множестве
(также можно использовать латинские буквы). Тогда раскраска является функцией, определенной на множестве вершин графа и принимающей значения в множестве  . Раскраску можно также рассматривать как разбиение множества вершин
. Раскраску можно также рассматривать как разбиение множества вершин 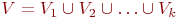 , где
, где 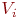 - множество вершин цвета
- множество вершин цвета  . Множества
. Множества  в наименьшее число цветов. Это число называется хроматическим числом графа и обозначается
в наименьшее число цветов. Это число называется хроматическим числом графа и обозначается 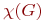 .
.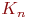 все вершины должны иметь разные цвета, поэтому
все вершины должны иметь разные цвета, поэтому 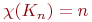 . Если в каком-нибудь графе имеется полный подграф с
. Если в каком-нибудь графе имеется полный подграф с 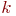 вершинами, то для раскраски этого подграфа необходимо
вершинами, то для раскраски этого подграфа необходимо 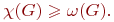
 , n – размерность, k - значность
, n – размерность, k - значность называется вложимым в булево пространство Нn<VH,UH> или кубируемым, если существует соответствие ϕ между вершинами графа G и гиперкуба Hnтакое, что если (
называется вложимым в булево пространство Нn<VH,UH> или кубируемым, если существует соответствие ϕ между вершинами графа G и гиперкуба Hnтакое, что если ( .Так как n-куб является двудольным графом, то в соответствии с теоремой Кёнига все его простые циклы четны, и поэтому любой граф, который содержит подграф, являющийся нечетным циклом, некубируем. Следовательно циклы нечетной длины и граф Кёнига К2,3
.Так как n-куб является двудольным графом, то в соответствии с теоремой Кёнига все его простые циклы четны, и поэтому любой граф, который содержит подграф, являющийся нечетным циклом, некубируем. Следовательно циклы нечетной длины и граф Кёнига К2,3  являются запрещенными фигурами вложения графа в булево пространство. Под запрещенной фигурой в данном случае понимаем критически невложимый граф, т.е. некубируемый граф, у которого все частичные графы кубируемые.
являются запрещенными фигурами вложения графа в булево пространство. Под запрещенной фигурой в данном случае понимаем критически невложимый граф, т.е. некубируемый граф, у которого все частичные графы кубируемые. 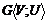 ;
;  называется изоморфным если существует такое взаимно однозначное соответствие между вершинами V и V’, что вершины Va и Vв соединены дугой (Va,Vв) в одном из графов в том и только в том случае когда соответствующие им вершины V’a и V’в соединены дугой (V’a,V’в) в другом графе.
называется изоморфным если существует такое взаимно однозначное соответствие между вершинами V и V’, что вершины Va и Vв соединены дугой (Va,Vв) в одном из графов в том и только в том случае когда соответствующие им вершины V’a и V’в соединены дугой (V’a,V’в) в другом графе.  граф G изоморфен графу G’. Два графа гомеоморфные если они изоморфны с точностью степени два. Вложить граф в гиперкуб это значит установить изоморфизм между графом и гиперкубом. Гиперкубом – называется граф каждая вершина которого соответствует области пространства, и две вершины соединены ребром если они соответствуют соседним областям имеющих общую границу. Размерность пространства- размерность гиперкуба, n-значность логики.
граф G изоморфен графу G’. Два графа гомеоморфные если они изоморфны с точностью степени два. Вложить граф в гиперкуб это значит установить изоморфизм между графом и гиперкубом. Гиперкубом – называется граф каждая вершина которого соответствует области пространства, и две вершины соединены ребром если они соответствуют соседним областям имеющих общую границу. Размерность пространства- размерность гиперкуба, n-значность логики. определяется неравенством
определяется неравенством  , где ] [ -целая часть, |V|=n, si- степень i –ой вершины. Чтобы определить, какие ребра необходимо удалить для преобразования графа в планарный, выделим все запрещенные фигуры и построим двумерную таблицу, каждая строка которой взаимно однозначно соответствует запрещенной фигуре Qi, a столбец – ребру Pi. тогда покрытие строк столбцами этой таблицы определит, какие ребра необходимо удалить, чтобы граф стал планарным. Минимальное покрытие будет соответствовать минимальному решению, так как удаление любого ребра выводит запрещенную фигуру из класса подграфов, гомеоморфных F5 или К3,3.
, где ] [ -целая часть, |V|=n, si- степень i –ой вершины. Чтобы определить, какие ребра необходимо удалить для преобразования графа в планарный, выделим все запрещенные фигуры и построим двумерную таблицу, каждая строка которой взаимно однозначно соответствует запрещенной фигуре Qi, a столбец – ребру Pi. тогда покрытие строк столбцами этой таблицы определит, какие ребра необходимо удалить, чтобы граф стал планарным. Минимальное покрытие будет соответствовать минимальному решению, так как удаление любого ребра выводит запрещенную фигуру из класса подграфов, гомеоморфных F5 или К3,3.
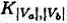 , построенного на носителях
, построенного на носителях