Рассмотрим второй подход к решению задачи выбора оптимального портфеля, а именно, будем выбирать «главный» критерий, фиксируя значение другого критерия.
Пусть уровень доходности 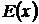 фиксируется и ищутся портфели с минимальным риском
фиксируется и ищутся портфели с минимальным риском  . Такие портфели называются минимальными (по риску), а их оценки составляют минимальную границу критериального множества. Геометрически минимальная граница выглядит следующим образом:
. Такие портфели называются минимальными (по риску), а их оценки составляют минимальную границу критериального множества. Геометрически минимальная граница выглядит следующим образом:
Рис.6.
Здесь для любого  определяется портфель с оценкой вида
определяется портфель с оценкой вида  , который имеет наименьшую дисперсию. Множество таких оценок представляет собой дугу
, который имеет наименьшую дисперсию. Множество таких оценок представляет собой дугу  , которая и является минимальной границей. Причем показано (Марковиц), что эту границу можно представить на плоскости оценок графиком непрерывной функции вида
, которая и является минимальной границей. Причем показано (Марковиц), что эту границу можно представить на плоскости оценок графиком непрерывной функции вида 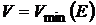 .
.
Отметим также, что эффективная граница  является частью минимальной границы критериального множества.
является частью минимальной границы критериального множества.
Перейдем теперь к построению оценок портфелей состоящих из двух активов. Начнем с модели Блека.
МОДЕЛЬ БЛЕКА ДЛЯ ДВУХ АКТИВОВ
Критериальное множество
Рассмотрим рынок из двух активов 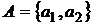 с параметрами
с параметрами  и
и  . Портфель
. Портфель  описывается парой
описывается парой  с основным ограничением
с основным ограничением  . Представим последнее условие в параметрическом виде:
. Представим последнее условие в параметрическом виде:

где  . Тогда портфель
. Тогда портфель  будет описываться парой:
будет описываться парой:
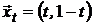 . (5)
. (5)
Вычислим доходность  и риск
и риск  такого портфеля:
такого портфеля:
 ; (6)
; (6)
 . (7)
. (7)
Учитывая, что  равенство (7) можно переписать в виде:
равенство (7) можно переписать в виде:

 (7¢)
(7¢)
Из последнего равенства следует, что риск  портфеля зависит не только от рисков активов
портфеля зависит не только от рисков активов  и
и  , но и от коэффициента корреляции
, но и от коэффициента корреляции  .
.
Равенства (6) и (7) определяют на критериальной плоскости  критериальное множество
критериальное множество  , которое, как легко увидеть, представляет собой линию второго порядка вида
, которое, как легко увидеть, представляет собой линию второго порядка вида  . В этом можно убедиться, выразив
. В этом можно убедиться, выразив  из уравнения (6) и подставив полученное выражение в (7¢). Однако при этом получается достаточно громоздкое выражение, поэтому проведем предварительно исследование этой линии при различных значениях коэффициента корреляции
из уравнения (6) и подставив полученное выражение в (7¢). Однако при этом получается достаточно громоздкое выражение, поэтому проведем предварительно исследование этой линии при различных значениях коэффициента корреляции  .
.
3.2. Коэффициент корреляции 
В этом случае, уравнение (7’) примет вид:
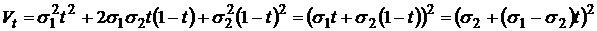 .
.
Подставив в последнее равенство параметр t из равенства (6):
 ,
,
получим
 . (8)
. (8)
То есть, в невырожденном случае  , критериальное множество
, критериальное множество  представляет собой параболу на критериальной плоскости
представляет собой параболу на критериальной плоскости  :
:
Рис.7.
Эта парабола имеет вершину  , с нулевым риском
, с нулевым риском  и доходностью
и доходностью  (следует из равенства V(E) =0), и такой оценке соответствует портфель:
(следует из равенства V(E) =0), и такой оценке соответствует портфель:
 . (9)
. (9)
Видно, что полное устранение риска в этом случае достигается только с использованием коротких позиций, так как одно из чисел  и
и  обязательно отрицательно.
обязательно отрицательно.
С другой стороны, к полному устранению риска нужно подходить осторожно, так как, например, в случае

получаем, что доходность такого портфеля будет отрицательной 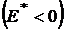 , поэтому такое устранение риска является бессмысленным.
, поэтому такое устранение риска является бессмысленным.
Если же риск измерять не дисперсией, а стандартным отклонением  , то из формулы (8) получаем:
, то из формулы (8) получаем:
 . (10)
. (10)
В этом случае, критериальное множество представляет собой пару лучей с вершиной в точке  :
:
Рис.8.
Таким образом, в случае  минимальная граница совпадает с критериальным множеством, а эффективная граница представляет собой «правую ветвь» параболы на
минимальная граница совпадает с критериальным множеством, а эффективная граница представляет собой «правую ветвь» параболы на  , или «правый луч» на плоскости
, или «правый луч» на плоскости  .
.
3.3. Коэффициент корреляции  .
.
В этом случае оценки портфелей имеют вид:
 ,
,
 . (11)
. (11)
Выражая t через Et и подставляя в  , получим параболу с вершиной Q*. Найдем координаты вершины этой параболы из условия
, получим параболу с вершиной Q*. Найдем координаты вершины этой параболы из условия  , а именно
, а именно

или
 .
.
Тогда
 ,
,
и
 .
.
Таким образом, хотя  , то есть риск портфеля
, то есть риск портфеля  меньше риска каждого из активов, но полностью устранить риск нельзя.
меньше риска каждого из активов, но полностью устранить риск нельзя.
Критериальное множество (парабола) в этом случае имеет вид:
Рис.9.
На плоскости  получаем кривую
получаем кривую
 (11')
(11')
которая представляет собой «верхнюю» ветвь гиперболы.
Рис.10.
Отметим, что здесь  .
.
Как и в §3.2. минимальная граница совпадает с самим критериальным множеством, а эффективная граница – это «правая ветвь» параболы или гиперболы (соответственно).
3.4. Коэффициент корреляции 
В этом случае
 ,
,
 , (12)
, (12)
или
 . (12')
. (12')
Это означает, что на плоскости (E,V) критериальное множество будет параболой с вершиной  , в которой
, в которой  вычисляется из условия
вычисляется из условия

или
 .
.
Тогда
 ,
,
и парабола имеет вид:
Рис.11.
Здесь  и риск можно устранить полностью
и риск можно устранить полностью  только при использовании длинных позиций, так как
только при использовании длинных позиций, так как 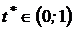 .
.
На плоскости  получаем пару лучей:
получаем пару лучей:
Рис.12.
Аналогичный анализ можно провести и для остальных  . При этом следует, что:
. При этом следует, что:
а) полностью устранить риск можно лишь при 
б) в общем случае на плоскости  критериальное множество будет параболой, а на
критериальное множество будет параболой, а на  - гиперболой;
- гиперболой;
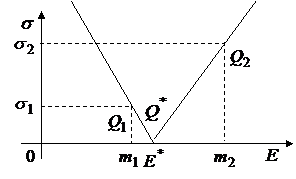
в) при  вершина
вершина  будет лежать вне дуги
будет лежать вне дуги  , а при
, а при  - внутри дуги
- внутри дуги  .
.



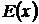 фиксируется и ищутся портфели с минимальным риском
фиксируется и ищутся портфели с минимальным риском  . Такие портфели называются минимальными (по риску), а их оценки составляют минимальную границу критериального множества. Геометрически минимальная граница выглядит следующим образом:
. Такие портфели называются минимальными (по риску), а их оценки составляют минимальную границу критериального множества. Геометрически минимальная граница выглядит следующим образом:
 определяется портфель с оценкой вида
определяется портфель с оценкой вида  , который имеет наименьшую дисперсию. Множество таких оценок представляет собой дугу
, который имеет наименьшую дисперсию. Множество таких оценок представляет собой дугу  , которая и является минимальной границей. Причем показано (Марковиц), что эту границу можно представить на плоскости оценок графиком непрерывной функции вида
, которая и является минимальной границей. Причем показано (Марковиц), что эту границу можно представить на плоскости оценок графиком непрерывной функции вида 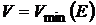 .
. является частью минимальной границы критериального множества.
является частью минимальной границы критериального множества.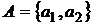 с параметрами
с параметрами  и
и  . Портфель
. Портфель  описывается парой
описывается парой  с основным ограничением
с основным ограничением  . Представим последнее условие в параметрическом виде:
. Представим последнее условие в параметрическом виде:
 . Тогда портфель
. Тогда портфель 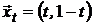 . (5)
. (5) и риск
и риск  такого портфеля:
такого портфеля: ; (6)
; (6) . (7)
. (7) равенство (7) можно переписать в виде:
равенство (7) можно переписать в виде:
 (7¢)
(7¢) портфеля зависит не только от рисков активов
портфеля зависит не только от рисков активов  и
и  , но и от коэффициента корреляции
, но и от коэффициента корреляции  .
. критериальное множество
критериальное множество  , которое, как легко увидеть, представляет собой линию второго порядка вида
, которое, как легко увидеть, представляет собой линию второго порядка вида  . В этом можно убедиться, выразив
. В этом можно убедиться, выразив  из уравнения (6) и подставив полученное выражение в (7¢). Однако при этом получается достаточно громоздкое выражение, поэтому проведем предварительно исследование этой линии при различных значениях коэффициента корреляции
из уравнения (6) и подставив полученное выражение в (7¢). Однако при этом получается достаточно громоздкое выражение, поэтому проведем предварительно исследование этой линии при различных значениях коэффициента корреляции 
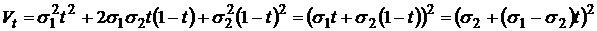 .
. ,
, . (8)
. (8) , критериальное множество
, критериальное множество 
 , с нулевым риском
, с нулевым риском  и доходностью
и доходностью  (следует из равенства V(E) =0), и такой оценке соответствует портфель:
(следует из равенства V(E) =0), и такой оценке соответствует портфель: . (9)
. (9) и
и  обязательно отрицательно.
обязательно отрицательно.
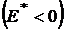 , поэтому такое устранение риска является бессмысленным.
, поэтому такое устранение риска является бессмысленным. , то из формулы (8) получаем:
, то из формулы (8) получаем: . (10)
. (10)
 , или «правый луч» на плоскости
, или «правый луч» на плоскости  .
. .
. ,
, . (11)
. (11) , а именно
, а именно
 .
. ,
, .
. , то есть риск портфеля
, то есть риск портфеля  меньше риска каждого из активов, но полностью устранить риск нельзя.
меньше риска каждого из активов, но полностью устранить риск нельзя.
 получаем кривую
получаем кривую (11')
(11')
 .
.
 ,
, , (12)
, (12) . (12')
. (12') , в которой
, в которой  вычисляется из условия
вычисляется из условия
 .
. ,
,
 и риск можно устранить полностью
и риск можно устранить полностью  только при использовании длинных позиций, так как
только при использовании длинных позиций, так как 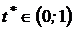 .
.
 . При этом следует, что:
. При этом следует, что:
 вершина
вершина  будет лежать вне дуги
будет лежать вне дуги  , а при
, а при  - внутри дуги
- внутри дуги 


