Расчет переходного процесса
В сложной цепи ПОСТОЯННОГО ТОКА
Методическое пособие
к расчетно-графической работе
Хабаровск
Рецензенты: Кафедра "Электросвязь, микроэлектроника и метрология" Хабаровского филиала Сибирского государственного университета телекоммуникаций и информатики, заведующий кафедрой, профессор В.А. Константинов
Инженер дорожной электротехнической лаборатории Дальневосточной железной дороги В.А. Деев
Дается общий обзор методов расчета переходных процессов. Подробно рассматриваются методы: классический, операторный и переменных состояния. Приводятся варианты задания на расчетно-графическую работу.
Разделы 1, 2, 3 и 5 написаны доцентом В.С. Матющенко, раздел 4 и введение – доцентом О.Г. Заволока.
Пособие предназначено для студентов ДВГУПС, изучающих теоретические основы электротехники.
Издательство Дальневосточного государственного университета путей сообщения (ДВГУПС), 2001
ОГЛАВЛЕНИЕ
Предисловие
Введение
1. РАСЧЕТ ПЕРЕХОДНОГО ПРОЦЕССА КЛАССИЧЕСКИМ МЕТОДОМ
2. Операторный метод
3. Определение тока в ёмкости
4. МЕТОД ПЕРЕМЕННЫХ СОСТОЯНИЯ
4.1. Основные теоретические сведения
4.2. Составление уравнений состояния с помощью законов Кирхгофа
4.3. Составление уравнений состояния методом наложения
4.4. Решение уравнений состояния
5. ПОСТРОЕНИЕ КРИВОЙ ТОКА ПЕРЕХОДНОГО РЕЖИМА
ПРИЛОЖЕНИЕ. Задание на расчетно-графическую работу
СПИСОК ЛИТЕРАТУРЫ
Предисловие
Переходные процессы в электротехнических установках, причиной которых являются различного рода переключения, в практике инженера-электрика встречаются довольно часто. Анализ возникающих при этом режимов обычно представляет сложную задачу и требует применения таких разделов математики, как дифференциальные уравнения, операционное исчисление, преобразование Фурье, интеграл Дюамеля.
Цель настоящего пособия заключается в оказании помощи студентам в их самостоятельной работе при изучении этого, одного из наиболее сложных в теории линейных электрических цепей, раздела.
В теоретической электротехнике разработаны различные методы расчета переходных процессов. Во введении дается их общий обзор и особенности применения. Три метода – классический, операторный и переменных состояния подробно рассматриваются применительно к предусмотренной учебным планом расчетно-графической работе, задание на которую помещено в приложении.
Изложение ведется на примере схемы второго порядка; наиболее трудные места поясняются конкретными расчетами. Для численного интегрирования уравнений состояния предусматривается применение ЭВМ.
Пособие не ставит целью заменить учебник, и для успешного усвоения рассматриваемых вопросов его одного недостаточно. Требуется изучение учебной литературы и самостоятельное решение задач.
Введение
Переходным называют процесс, возникающий в электрической цепи, содержащей реактивные элементы, при переходе от одного установившегося режима к другому. Переходные процессы могут быть вызваны подключением цепи в целом к зажимам источника или включением элементов в цепь, находящуюся под действием источников, либо отключением отдельных элементов. Такие изменения называют коммутациями и считают их происходящими мгновенно. Начало отсчета времени переходных процессов  начинается с момента коммутации.
начинается с момента коммутации.
Определение значений токов и напряжений при переходных процессах является весьма важной задачей с точки зрения практики, так как они в отдельных случаях могут значительно превышать их значения в установившихся режимах и вследствие этого приводить к повреждению элементов цепи. Скорость протекания переходных процессов в электромагнитных устройствах систем передачи информации определяет их быстродействие. Методы расчета переходных процессов отличаются от принятых для расчета установившихся процессов.
С математической точки зрения задача расчета переходного процесса сводится к решению системы дифференциальных уравнений, составленных для цепи после коммутации на основании законов Кирхгофа. Производные в уравнениях по законам Кирхгофа появляются при подстановке выражений связи между токами и напряжениями для индуктивностей и емкостей в общей форме:  . В случае расчета линейной электрической цепи все дифференциальные уравнения, входящие в систему, – линейные.
. В случае расчета линейной электрической цепи все дифференциальные уравнения, входящие в систему, – линейные.
Существенной особенностью решения дифференциальных уравнений, описывающих цепь во время переходного процесса, является необходимость определения начальных условий – значений искомых токов и напряжений в момент  , которые можно получить, рассматривая состояние цепи в момент коммутации. Большое значение при расчете начальных условий имеют два закона коммутации:
, которые можно получить, рассматривая состояние цепи в момент коммутации. Большое значение при расчете начальных условий имеют два закона коммутации:
1. ток в индуктивности в момент коммутации сохраняет значение, которое он имел непосредственно перед коммутацией;
2. напряжение на емкости в момент коммутации сохраняет значение, которое оно имело непосредственно перед коммутацией.
Законы коммутации позволяют определить начальные условия для токов в индуктивностях и напряжений на емкостях на основании расчета состояния цепи непосредственно перед коммутацией. Начальные условия для других величин: токов и напряжений на резисторах, токов в емкостях и напряжений на индуктивностях – находят решением системы уравнений, составленных по законам Кирхгофа для момента коммутации с учетом законов коммутации.
В зависимости от конкретного подхода к определению решения системы дифференциальных уравнений различают следующие методы расчета переходных процессов: классический; операторный; переменных состояния; с помощью интеграла Дюамеля; спектральный (частотный).
Остановимся подробнее на особенностях каждого метода.
Классический метод заключается в интегрировании дифференциальных уравнений, описывающих цепь, и определении постоянных интегрирования из начальных условий. Искомые напряжения и токи представляются при этом в виде  и
и 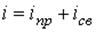 , где
, где  – принужденные составляющие;
– принужденные составляющие;  – свободные составляющие.
– свободные составляющие.
Математически принужденные составляющие – это частное решение неоднородного дифференциального уравнения. В случае постоянных или периодических источников принужденные составляющие фактически представляют собой токи и напряжения установившегося режима и могут быть найдены из расчета этого режима.
Свободные составляющие представляют собой общее решение однородного дифференциального уравнения, и их вид определяется числом и значениями корней характеристического уравнения.
Характеристическое уравнение цепи определяется только топологией цепи после коммутации и значением ее параметров и имеет одинаковый вид для тока и напряжения в любой ветви. Получить характеристическое уравнение можно из исходной системы дифференциальных уравнений путем последовательного сведения системы к одному уравнению относительно одного какого-либо тока или напряжения. Однако этот путь сопряжен с громоздкими алгебраическими преобразованиями. Поэтому в пособии рассматривается более простой метод получения характеристического уравнения цепи.
После вычисления корней характеристического уравнения и определения на их основании закона изменения свободных составляющих необходимо найти постоянные интегрирования, входящие в их выражения. Это можно сделать, если известны начальные условия. Если число корней характеристического уравнения больше одного, то необходимо иметь не только начальное условие искомого тока или напряжения, но и его производных. При этом порядок производных, начальное значение которых необходимо знать, на единицу меньше числа корней характеристического уравнения. То есть при двух корнях необходимо вычислять начальное условие первой производной, при трех корнях – первой и второй и т.д.
Необходимость определения начальных условий не только искомых токов и напряжений, но их производных представляет собой основную сложность расчета переходных процессов классическим методом особенно для цепей с несколькими реактивными элементами.
Избежать необходимости многократного решения систем алгебраических уравнений для нахождения начальных условий токов и напряжений и их производных, а также для определения постоянных интегрирования позволяет операторный метод.
Так как дифференциальные уравнения, описывающие состояние линейных цепей во время переходных процессов, представляют собой линейные уравнения с постоянными коэффициентами, то их можно интегрировать методом, основанным на преобразовании Лапласа.
В этом случае действительные функции времени 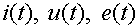 , называемые оригиналами, заменяют их операторными изображениями
, называемые оригиналами, заменяют их операторными изображениями  , где
, где  – некоторое комплексное число, называемое оператором. Связь между оригиналом и его изображением устанавливается с помощью интеграла Лапласа
– некоторое комплексное число, называемое оператором. Связь между оригиналом и его изображением устанавливается с помощью интеграла Лапласа
 .
.
Достоинство преобразования Лапласа в том, что изображение производной функции имеет вид:  , где
, где  – начальное условие заданной функции.
– начальное условие заданной функции.
Применение этой формулы для выражений связи между токами и напряжениями в индуктивности и емкости дает следующие уравнения:
 .
.
Приведенные выражения формально совпадают по виду с законом Ома для участка цепи, содержащего источник энергии. Это дает возможность построить операторные схемы замещения реактивных элементов. И таким образом при составлении уравнений цепи в операторной форме автоматически учитываются начальные условия – значения токов в индуктивностях и напряжения на емкостях при  , которые определяются законами коммутации.
, которые определяются законами коммутации.
Применение преобразования Лапласа к системе дифференциальных уравнений переходного процесса сводит ее к системе алгебраических уравнений для изображений, в которых отражены и начальные условия. Операторные схемы замещения реактивных элементов и тот факт, что вследствие линейности законы Кирхгофа для оригиналов и изображений имеют аналогичный вид:
 ,
,
позволяет составлять систему уравнений для изображения сразу по обычным правилам.
После составления расчетной системы уравнений можно определить изображение искомой величины с помощью чисто алгебраических преобразований. По найденному изображению находят оригинал искомой величины. Обычно в случае расчета линейных цепей это выполняют с помощью теоремы разложения, применение которой рассмотрено в работе.
Применение операторного метода не требует определения постоянных интегрирования из начальных условий, как это необходимо в классическом методе, а также вычисления значений производных в момент коммутации. Однако сложность операторного метода заключается в необходимости проведения трудоемких алгебраических преобразований над изображениями, приводящих в ряде случаев к громоздким выражениям, что ограничивает применение вычислительной техники. Определенную трудность представляет собой и этап перехода от изображения к оригиналу.
Метод переменных состояния позволяет рассчитывать переходные процессы в сложных цепях с произвольной конфигурацией, включающей любое число реактивных элементов, путем интегрирования уравнений состояния. Такими уравнениями называют дифференциальные уравнения, составленные относительно переменных состояния – токов в индуктивностях  и напряжений на емкостях
и напряжений на емкостях  .
.
Совокупность переменных состояния цепи должна образовывать независимую систему, позволяющую единственным образом выразить все остальные токи и напряжения цепи. Для этого необходимо, чтобы в цепи отсутствовали контуры, состоящие только из емкостей и источников ЭДС, и сечения, в состав которых входили бы только индуктивности и источники тока.
Общий путь расчета переходного процесса методом переменных состояния основан на составлении дифференциальных уравнений первого порядка относительно переменных состояния, записанных в нормальной форме Коши. Две методики формирования уравнений состояния представлены в работе.
Аналитическое решение уравнений состояния методом непосредственного интегрирования основано на определении постоянных интегрирования в общем решении дифференциального уравнения путем решения системы алгебраических уравнений, выражающих искомую величину и ее младшие производные при  . Такой подход целесообразно применять лишь к уравнениям невысокого порядка при простых законах изменения, действующих в цепи источников.
. Такой подход целесообразно применять лишь к уравнениям невысокого порядка при простых законах изменения, действующих в цепи источников.
Наиболее компактно аналитическое решение уравнений состояния можно получить на основе матричного аппарата. Однако в этом случае возникают трудности в определении такой многомерной функции как матричная экспонента.
Уравнения состояния цепей, число реактивных элементов в которых больше двух-трех, проще решаются не аналитическими, а численными методами. Интегрирование дифференциальных уравнений, записанных в нормальной форме Коши, выполняется в этом случае с помощью стандартных методов численного интегрирования на ЭВМ. Особенности применения численных методов рассмотрены в данном пособии.
При анализе переходных процессов, возникающих в пассивных цепях, при импульсных воздействиях произвольной формы находит применение расчет с помощью интеграла Дюамеля. При включении пассивного двухполюсника на напряжение произвольной формы  ток на входе цепи можно определить по следующему выражению (одна из форм интеграла Дюамеля)
ток на входе цепи можно определить по следующему выражению (одна из форм интеграла Дюамеля)
 ,
,
где  – переходная проводимость цепи;
– переходная проводимость цепи;  – выражение производной функции входного напряжения
– выражение производной функции входного напряжения  .
.
Переходная проводимость  является так называемой переходной характеристикой (функцией) цепи и численно равна току в цепи во время переходного процесса, возникающего при включении этой цепи на постоянное единичное напряжение. Переходные характеристики могут быть определены и для напряжений на каком-либо участке цепи. Расчет переходной характеристики сводится к решению простой задачи – анализу переходного процесса при включении цепи на постоянное напряжение при нулевых начальных условиях.
является так называемой переходной характеристикой (функцией) цепи и численно равна току в цепи во время переходного процесса, возникающего при включении этой цепи на постоянное единичное напряжение. Переходные характеристики могут быть определены и для напряжений на каком-либо участке цепи. Расчет переходной характеристики сводится к решению простой задачи – анализу переходного процесса при включении цепи на постоянное напряжение при нулевых начальных условиях.
Особенно эффективно применение интеграла Дюамеля для расчета переходных процессов при воздействии на цепь напряжения, изменение которого определяется кусочно-аналитической функцией, т.е. функцией, имеющей разрывы непрерывности первого рода.
Спектральный (частотный) метод расчета переходных процессов не требует составления дифференциальных уравнений цепи, а базируется на использовании одностороннего интегрального преобразования Фурье.
Пусть некоторая пассивная цепь включается на напряжение  , для которого можно определить его частотную характеристику (спектральную плотность)
, для которого можно определить его частотную характеристику (спектральную плотность)
 .
.
Если для цепи известно комплексное сопротивление  как функция частоты, то частотную характеристику тока в цепи можно найти по формуле
как функция частоты, то частотную характеристику тока в цепи можно найти по формуле
 .
.
Искомый ток переходного процесса находят с помощью обратного преобразования Фурье:
 .
.
Сам по себе этот метод не дает каких-либо существенных преимуществ по сравнению с рассмотренным ранее операторным методом. Достоинством частотного метода является то, что он позволяет найти ток  для сложной линейной электрической цепи, для которой экспериментально получена зависимость комплексного сопротивления от частоты
для сложной линейной электрической цепи, для которой экспериментально получена зависимость комплексного сопротивления от частоты  .
.
Операторный метод
В основу операторного метода положен математический аппарат операционного исчисления, когда функции времени и описывающие их дифференциальные уравнения заменяются соответственно алгебраическими функциями комплексного переменного и алгебраическими уравнениями. Решения последних, так называемые изображения, позволяют по определенным правилам записывать искомые функции времени – оригиналы.
Приложение операционного исчисления к задачам электротехники привело к созданию операторного метода, вообще не требующего составления дифференциальных уравнений. Реальные электрические схемы преобразуются в чисто математические – операторные схемы, расчет которых формально не отличается от расчета обыкновенных электрических цепей.
Составление операторных схем ведется по следующим правилам:
– операторная схема сохраняет конфигурацию послекоммутационной электрической цепи;
– сопротивления переносятся в операторную схему без изменения;
– индуктивность L заменяется элементом рL, последовательно с которым включается добавочная ЭДС Li (0), направленная по току;
– емкость С заменяется элементом 1 /рC, последовательно с которым включается добавочная ЭДС uC( 0 )/р, направленная против тока;
– ЭДС и токи заменяются их изображениями (рис. 4).
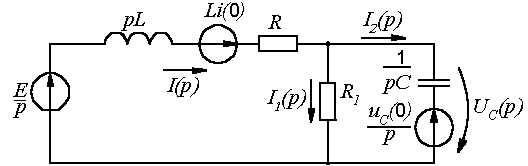
Рис. 4. Операторная схема
Полученная схема может быть рассчитана любым известным методом. Например, применение контурных токов приводит к следующим уравнениям:
 (13)
(13)
Операторные токи I(р) и I2(р) находятся из этой системы, а I 1 (р), если необходимо, по первому закону Кирхгофа в операторной форме:
I1(р)=I(р)–I2(р).
Изображение напряжения на конденсаторе определяется по закону Ома в операторной форме (рис. 4):
 . (14)
. (14)
Изображения токов из системы (13) удобнее всего находить с помощью определителей. Например, для тока I 2 (р) будем иметь:
 .
.
Раскрыв определители и упростив числитель и знаменатель в выражении I 2 (р), после проверки (как она выполняется, см. ниже) подставляем его в (14). В результате получаем выражение вида
 , (15)
, (15)
где а, b, d, f, g, h – некоторые числа.
Перед отысканием оригинала полученное изображение необходимо проверить с помощью предельных соотношений операционного исчисления:
1.  ,3)
,3) 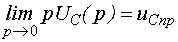 ,
,
2.  ,4)
,4)  .
.
По этим же формулам делается и упомянутая выше проверка тока I2(р).
Если задача имеет нулевые начальные условия, т.е. iL (0)=0 и uC (0)=0, что имеет место при подключении к источнику цепи с незаряженным конденсатором, как например на рис. 5, а, то операторная схема не содержит добавочных ЭДС (рис. 5, б), и для расчета можно использовать закон Ома:
 ,
,
 и т.д.
и т.д.

Рис. 5. Электрическая (а) и операторная (б) схемы с нулевыми начальными условиями
Приступаем к отысканию оригинала uC(t) по его изображению UC(р).
Так как знаменатель в формуле (15) имеет нулевой корень, используем следующую формулу разложения:
 . (16)
. (16)
Применение формулы покажем на конкретном числовом примере.
Предположим, что в результате всех проделанных вычислений мы получили следующее выражение:
 .
.
Для упрощения дальнейших выкладок рекомендуем разделить все члены дроби на коэффициент при р 2 знаменателя, т.е. на 4 · 10-4:
 . (17)
. (17)
В формуле разложения F 1 (р) и F 2 (р) – это полиномы, стоящие в числителе и знаменателе изображения:
F 1(р) = 1050 р 2 + 512000 р+ 1375 · 106,
F 2(р) =р 2 + 750 р+ 1,375 · 106.
Записываем их значения при р = 0:
F 1(0) = 1375 · 106, F 2(0) = 1,375 · 106.
Далее находим корни полинома – знаменателя, т.е. решаем уравнение F 2 (р)= 0:
р 2 + 750 р+ 1,375 · 106 = 0,
 .
.
Эти значения должны совпадать с корнями характеристического уравнения в классическом методе.
Примем: р 1 = – 375 +j 1111 = 1173 е j 108,7°,
р 2 = – 375– j 1111 = 1173 е– j 108,7°.
Найденные корни подставляем вместо р в числитель изображения UС (р), т.е. вычисляем F 1(р 1) и F 1(р 2):
F 1(р 1) =1050(-375+ j 1111)2+512000(-375+ j 1111)+1375 · 106=
=(34,62- j 306,1) · 106=308 · 106 е – j 83,5°,
F 1(р 2) =1050(-375- j 1111)2+512000(-375- j 1111)+1375 · 106=308 · 106 е j 83,5°.
Теперь дифференцируем полином, стоящий в скобках в знаменателе формулы (17), т.е. находим F 2? (р) = 2 р+ 750 и вычисляем его значения при
р =р 1 и р =р 2 :
F 2 (р 1) =2(-375+ j 1111)+750=1111· 2 j,
F 2 (р 2) =2(-375- j 1111)+750= -1111· 2 j.
Результат записываем именно в такой форме, выделяя в нем множитель 2 j.
Обращаем внимание на то, что каждая пара результатов в проведенных вычислениях – это сопряженные комплексные числа.
Подставляем найденные величины в формулу разложения (16):
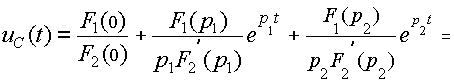

 .
.
Второе и третье слагаемые объединяем в одну дробь, вынося общие множители и собирая вместе соответствующие экспоненты:
 .
.
Вторая дробь в соответствии с формулой Эйлера

представляет собой синус выражения, стоящего в показателе степени экспоненты:
uC (t) =1000+236,3 e –375 tsin (1111 t -192,2°).
или
uC (t) =1000+236,3 e –375 tsin (1111 t +167,8°),
Подставляя сюда t= 0 и t ® ¥, проверяем соответствие полученного выражения моменту коммутации и установившемуся режиму:
 ,
,
 .
.
Определение тока в ЕМКОСТИ
Ток, протекающий через конденсатор (ток i2 в заданной схеме), можно рассчитать классическим или операторным методами (см. разд. 1, 2). Но если закон изменения напряжения на конденсаторе известен, его можно найти из уравнения
 . (19)
. (19)
Именно так и требуется сделать в настоящей работе.
После взятия производной от uC (t) приходится искать сумму
вида a sin (w t+y) + b cos (w t+y), которая легко находится символическим методом.
Например, при С = 4 мкФ применение формулы (19) к полученной ранее функции uC (t) приведет к выражению
i2 (t) = e -375 t [-0,354 sin (1111 t+ 167,8°) + 1,05 cos (1111 t+ 167,8°)].
Синус и косинус в квадратных скобках заменяем соответствующими им комплексными числами, учитывая, что cos (1111 t+ 167,8°) = sin (1111 t+ 257,8°), производим следующие вычисления:
-0,354 е j 167,8° +1,05 e j 257,8° = 0,346- j 0,0748+(-0,222- j 1,026)=
=0,124- j 1,10=1,11 e – j 83,6°.
Делаем обратный переход к синусоидальной функции времени:
i2 (t)=1,11 e –375 t sin (1111 t- 83,6°). (20)
При t =0 выражение (20) должно дать число, равное значению i2 (0), найденному в п. 2 разд. 1.
 .
.
МЕТОД ПЕРЕМЕННЫХ СОСТОЯНИЯ
Решение уравнений состояния
Аналитическое решение уравнений состояния вида (21) для цепей, порядок которых больше двух, весьма громоздко, поэтому чаще всего они решаются численными методами на ЭВМ. В этом случае решение дифференциальных уравнений, составленных в форме Коши, сводится к их численному интегрированию. Разработаны различные методы численного интегрирования, которые позволяют рассчитывать значения искомых переменных через малые промежутки – шаги интегрирования h и получать решение в виде таблиц значений переменных для отдельных (дискретных) моментов времени. Любой метод численного интегрирования предполагает, что известны значения искомых переменных в начальный момент времени t =0 (начальные условия задачи). К наиболее простым методам численного интегрирования относятся явные методы, в которых искомые переменные определяются по уже найденным на предыдущем шаге значениям. К одношаговым методам относятся алгоритмы Рунге-Кутта различного порядка.
Важной проблемой численного интегрирования является выбор шага интегрирования h. Выбор излишне малого шага увеличивает время расчета и накопление ошибок округления. При слишком большом шаге может наблюдаться резкое увеличение погрешностей, т.е. с каждым последующим шагом численное решение все более отличается от истинного. В этом случае говорят о численной неустойчивости алгоритма. Все явные методы имеют ограничение величины шага интегрирования по условию обеспечения устойчивости. Оценить это значение можно, зная собственные значения основной матрицы 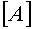 уравнений состояния (21).
уравнений состояния (21).
Собственные значения  матрицы
матрицы 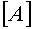 находят, решая уравнение
находят, решая уравнение
 , (28)
, (28)
где  – обозначение операции вычисления определителя;
– обозначение операции вычисления определителя; 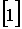 – единичная матрица того же порядка, что и
– единичная матрица того же порядка, что и 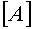 .
.
Собственные значения матрицы 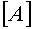 совпадают с корнями характеристического уравнения цепи.
совпадают с корнями характеристического уравнения цепи.
Наиболее просто определить величину шага интегрирования из условий обеспечения устойчивости для метода Рунге-Кутта первого порядка (метод Эйлера). При действительных собственных значениях матрицы 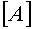 необходимо выбирать шаг из условия
необходимо выбирать шаг из условия  , где
, где  – максимальное по абсолютной величине собственное значение матрицы
– максимальное по абсолютной величине собственное значение матрицы 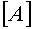 . При наличии в собственных значениях комплексных величин вида
. При наличии в собственных значениях комплексных величин вида  шаг должен быть еще и меньше минимального из значений, вычисленных по формуле
шаг должен быть еще и меньше минимального из значений, вычисленных по формуле  .
.
Методы Рунге-Кутта более высоких порядков сохраняют численную устойчивость и при несколько больших величинах шага интегрирования. Поэтому, выбрав шаг и проверив его по описанным соотношениям, можно быть уверенным, что решение будет сохранять устойчивость при применении любого явного метода численного интегрирования.
Оценим по критерию устойчивости шаг интегрирования уравнений состояния для цепи, изображенной на рис. 2, при заданных ранее величинах.
Подставляя в уравнение (28) основную матрицу 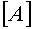 из (26), записываем:
из (26), записываем:

Раскрывая определитель, получаем (–250–l)(–500–l)+125 · 104 = 0 или l 2+750l +1375000 = 0.
Решая полученное квадратное уравнение, находим собственные значения основной матрицы цепи l = –375± j 1111.
Так как собственные значения представляют сопряженные комплексные величины, то шаг интегрирования должен удовлетворять условию

или h £5,45 · 10–4с = 0,545 мс. Для удобства расчетов и снижения погрешности интегрирования принимаем шаг h = 0,1 мс.
На кафедре ТОЭ ДВГУПС разработана программа LIN (автор программы О.Г. Заволока), предназначенная для численного интегрирования уравнений состояния линейных электрических цепей с постоянными источниками. Перед выполнением расчетов с помощью данной программы необходимо подготовить следующие исходные данные:
- основную матрицу
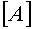 ;
; - матрицу источников
 ;
; - начальные значения переменных состояния iL (0) и uС (0);
- шаг интегрирования
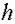 ;
; - шаг вывода и время интегрирования.
Две последние величины определяют, с каким интервалом будут выводиться на печать результаты вычислений и момент окончания расчетов. Например, если рассчитываем периодический процесс и хотим вывести на печать результаты интегрирования в 10 точках в течение одного периода синусоидальной составляющей, то шаг вывода и время окончания расчетов определяем следующим образом:
- период колебания
 ;
; - время окончания
 ;
; - шаг вывода
 .
.
Для рассматриваемого примера (w = 1111 рад/с) получаем  с = 5,66 мс, принимаем
с = 5,66 мс, принимаем  6 мс,
6 мс,  мс.
мс.
Следует отметить, что шаг вывода не должен быть меньше шага интегрирования.
Ввод данных при работе с программой LIN осуществляется в диалоговом режиме и при наличии подготовленных исходных данных не вызывает затруднений. Значения шагов интегрирования и вывода, времени окончания расчетов должны быть выражены в миллисекундах. Результаты расчетов в виде таблицы выводятся на экран и могут быть распечатаны.
В качестве образца (табл.1) приведены выводимые на печать результаты расчета контрольного примера, рассматриваемого в работе. Они включают исходные данные, вводимые пользователем. Переменные состояния в таблице результатов расчета обозначены символом Х с индексами 1 и 2. Так как при составлении уравнений состояния в качестве первой переменной состояния применяется ток i, а второй – напряжение uC, то Х[1] соответствует i, Х[2] – uC.
Таблица 1
Результаты расчетов
| Основная матрица А
-250.000000 -5.000000000
250000.000 -500.000000
|
| Вектор источников
5500.00000 0.0
|
| Начальные условия
1.00000000 1050.00000
|
| Шаг интегрирования – ввод: 0.100 мс; расчет: 0.100 мс
Шаг вывода – ввод: 0.600 мс; расчет: 0.600 мс
Время окончания – ввод: 6.000 мс; расчет: 6.000 мс
|
| Т, мс
0.000
0.600
1.200
1.800
2.400
3.000
3.600
4.200
4.800
5.400
6.000
| Х[1]
1.00000000
1.205777
1.640769
2.055534
2.298759
2.339575
2.235716
2.079334
1.949275
1.885748
1.888941
| Х[2]
1050.00000
917.4994
864.5686
882.6195
939.0260
998.3144
1036.7631
1047.2177
1035.8235
1014.8562
995.8044
|
ПРИЛОЖЕНИЕ
ЗАДАНИЕ НА РАСЧЕТНО-ГРАФИЧЕСКУЮ РАБОТУ
В электрической цепи с двумя реактивными элементами и источником постоянной ЭДС (рис. П1) происходит переключение ключа. Численные значения параметров цепи см. в табл. П1.





Рис. П1. Варианты расчетных схем. Номер схемы совпадает с первой цифрой варианта
Окончание приложения
Таблица П1
Численные значения параметров цепи
| Вторая цифра
варианта
| R1,
Ом
| R2,
Ом
| R3,
Ом
| E,
В
| Третья
цифра варианта
| L,
мГн
| C,
мкФ
|
|
|
|
|
|
|
|
| 9,4
|
|
|
|
|
|
|
|
| 1,3
|
|
|
|
|
|
|
|
| 2,7
|
|
|
|
|
|
|
|
| 6,7
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 5,4
|
|
|
|
|
|
|
|
|
|
Для заданной электрической цепи необходимо выполнить следующее.
1. Найти законы изменения токов первой и второй ветвей в переходном режиме классическим методом.
2. Найти закон изменения напряжения на конденсаторе операторным методом.
3. Найти закон изменения тока через конденсатор, используя уравнение связи между iС и uС.
4. Рассчитать переходный процесс методом переменных состояния.
5. По аналитическим выражениям построить кривые тока в индуктивности и напряжения на емкости методом вращающегося вектора. На эти кривые нанести точки, полученные в результате численного интегрирования уравнений состояния.
СПИСОК ЛИТЕРАТУРЫ
1. Основы теории цепей: Учеб.для вузов / Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил и др. – 5-е изд., перераб. – М.: Энергоатомиздат, 1989. – 528 с.
2. Попов В.П. Основы теории цепей: Учеб.для вузов. – 2-е изд., перераб. и доп. – М.: Высшая школа, 1998. – 575 с.
3. Шебес М.Р., Каблукова М.В.. Задачник по теории линейных электрических цепей. – 4-е изд., перераб. и доп. – М.: Высшая школа, 1990. – 544 с.
Расчет переходного процесса
в сложной цепи ПОСТОЯННОГО ТОКА
Методическое пособие
к расчетно-графической работе
Хабаровск
Рецензенты: Кафедра "Электросвязь, микроэлектроника и метрология" Хабаровского филиала Сибирского государственного университета телекоммуникаций и информатики, заведующий кафедрой, профессор В.А. Константинов
Инженер дорожной электротехнической лаборатории Дальневосточной железной дороги В.А. Деев
Дается общий обзор методов расчета переходных процессов. Подробно рассматриваются методы: классический, операторный и переменных состояния. Приводятся варианты задания на расчетно-графическую работу.
Разделы 1, 2, 3 и 5 написаны доцентом В.С. Матющенко, раздел 4 и введение – доцентом О.Г. Заволока.
Пособие предназначено для студентов ДВГУПС, изучающих теоретические основы электротехники.
Издательство Дальневосточного государственного университета путей сообщения (ДВГУПС), 2001
<



 начинается с момента коммутации.
начинается с момента коммутации. . В случае расчета линейной электрической цепи все дифференциальные уравнения, входящие в систему, – линейные.
. В случае расчета линейной электрической цепи все дифференциальные уравнения, входящие в систему, – линейные. , которые можно получить, рассматривая состояние цепи в момент коммутации. Большое значение при расчете начальных условий имеют два закона коммутации:
, которые можно получить, рассматривая состояние цепи в момент коммутации. Большое значение при расчете начальных условий имеют два закона коммутации: и
и 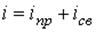 , где
, где  – принужденные составляющие;
– принужденные составляющие;  – свободные составляющие.
– свободные составляющие.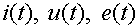 , называемые оригиналами, заменяют их операторными изображениями
, называемые оригиналами, заменяют их операторными изображениями  , где
, где  – некоторое комплексное число, называемое оператором. Связь между оригиналом и его изображением устанавливается с помощью интеграла Лапласа
– некоторое комплексное число, называемое оператором. Связь между оригиналом и его изображением устанавливается с помощью интеграла Лапласа .
. , где
, где  – начальное условие заданной функции.
– начальное условие заданной функции. .
. ,
, и напряжений на емкостях
и напряжений на емкостях  .
. ток на входе цепи можно определить по следующему выражению (одна из форм интеграла Дюамеля)
ток на входе цепи можно определить по следующему выражению (одна из форм интеграла Дюамеля) ,
, – переходная проводимость цепи;
– переходная проводимость цепи;  – выражение производной функции входного напряжения
– выражение производной функции входного напряжения  является так называемой переходной характеристикой (функцией) цепи и численно равна току в цепи во время переходного процесса, возникающего при включении этой цепи на постоянное единичное напряжение. Переходные характеристики могут быть определены и для напряжений на каком-либо участке цепи. Расчет переходной характеристики сводится к решению простой задачи – анализу переходного процесса при включении цепи на постоянное напряжение при нулевых начальных условиях.
является так называемой переходной характеристикой (функцией) цепи и численно равна току в цепи во время переходного процесса, возникающего при включении этой цепи на постоянное единичное напряжение. Переходные характеристики могут быть определены и для напряжений на каком-либо участке цепи. Расчет переходной характеристики сводится к решению простой задачи – анализу переходного процесса при включении цепи на постоянное напряжение при нулевых начальных условиях. .
. как функция частоты, то частотную характеристику тока в цепи можно найти по формуле
как функция частоты, то частотную характеристику тока в цепи можно найти по формуле .
. .
. для сложной линейной электрической цепи, для которой экспериментально получена зависимость комплексного сопротивления от частоты
для сложной линейной электрической цепи, для которой экспериментально получена зависимость комплексного сопротивления от частоты 
 (13)
(13) . (14)
. (14) .
. , (15)
, (15) ,3)
,3) 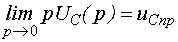 ,
, ,4)
,4)  .
. ,
, и т.д.
и т.д.
 . (16)
. (16) .
. . (17)
. (17) .
.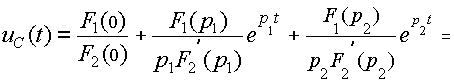

 .
. .
.
 ,
, .
. . (19)
. (19) .
.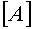 уравнений состояния (21).
уравнений состояния (21). матрицы
матрицы  , (28)
, (28) – обозначение операции вычисления определителя;
– обозначение операции вычисления определителя; 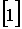 – единичная матрица того же порядка, что и
– единичная матрица того же порядка, что и  , где
, где  – максимальное по абсолютной величине собственное значение матрицы
– максимальное по абсолютной величине собственное значение матрицы  шаг должен быть еще и меньше минимального из значений, вычисленных по формуле
шаг должен быть еще и меньше минимального из значений, вычисленных по формуле  .
.

 ;
;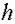 ;
; ;
; ;
; .
. с = 5,66 мс, принимаем
с = 5,66 мс, принимаем  6 мс,
6 мс,  мс.
мс.






