

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...
Топ:
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Интересное:
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Классический метод заключается в непосредственном решении дифференциальных уравнений I и II законов Кирхгофа, описывающих состояние цепи в переходном режиме. Применение метода рассмотрим на примере схемы, представленной на рис.1.

Рис. 1. Цепь второго порядка
Рекомендуется следующий порядок расчета.
1. t =0 _: момент непосредственно перед коммутацией; ключ еще разомкнут.
Расчет этого режима выполняем как в обычной цепи постоянного тока. Сопротивление у индуктивности принимаем равным нулю, а у емкости – бесконечно большим.
Так как ветвь с конденсатором для постоянного тока разорвана, то i 2(0_)=0, и ток замыкается по левому контуру:
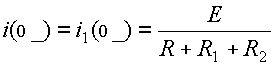 .
.
Напряжение на конденсаторе равно напряжению между верхним и нижним узлами схемы и может быть найдено по одной из формул:
 или
или  .
.
2. t = 0: момент коммутации; ключ только что замкнулся, сопротивление R2 закорочено, схема принимает следующий вид (рис. 2).


Рис. 2. Схема послекоммутационного режима
Значения токов, напряжений и их производных в момент коммутации называются начальными условиями. Определяются они с помощью законов Ома и Кирхгофа, записанных для момента коммутации.
Но начинать следует с законов коммутации:
 ,
,  .
.
Напоминаем, что эти уравнения относятся только к току в индуктивности и напряжению на емкости и для других элементов неприменимы.
Дальше для послекоммутационной цепи (рис. 2) записываем уравнения Кирхгофа:
 , (1)
, (1)
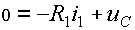 , (2)
, (2)
 . (3)
. (3)
При написании этих уравнений один из контуров рекомендуем выбирать так, чтобы в него не входила индуктивность. В этом случае уравнение, написанное для этого контура, не будет содержать производной тока, что облегчит отыскание начальных условий.
Теперь запишем уравнения (2) и (3) для момента коммутации
|
|
 ,
,  .
.
Так как uC (0) и i (0) известны, то i1 (0) и i2 (0) легко находятся из этих уравнений.
При расчете цепи второго порядка в решение дифференциального уравнения, определяющего ток (или напряжение) на любом участке, входят две постоянные интегрирования, для определения которых необходимо знать значения этого тока и его первой производной в момент коммутации. Имеющиеся уравнения (1) – (3) содержат производную тока i. Если требуется рассчитать только его, то написанных уравнений достаточно. При необходимости отыскания и других токов следует продифференцировать уравнения (2) и (3) и записать их совместно с (1) для момента t = 0
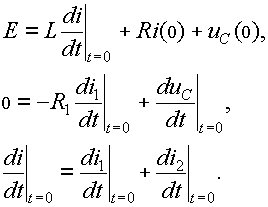
Добавляя к ним уравнение связи между током и напряжением на емкости в момент коммутации  , получаем возможность определения всех требуемых производных.
, получаем возможность определения всех требуемых производных.
Указание. В расчетно-графической работе следует найти производные всех токов и напряжения uС.
Часто встречается следующее ошибочное рассуждение: “А зачем решать все эти уравнения? Раз ток i (0) постоянный, то его производная автоматически равна нулю”. Ошибка здесь состоит в том, что мы не берем производную от i (0), а сначала ищем функцию di/dt и уже в нее подставляем t =0.
Величина  определяет скорость изменения тока (возрастания или убывания) в амперах в секунду в момент коммутации.
определяет скорость изменения тока (возрастания или убывания) в амперах в секунду в момент коммутации.
На графике она пропорциональна тангенсу угла наклона касательной, проведенной к кривой тока в точке t =0. Конечно, в некоторых случаях она может оказаться равной нулю.
3. t® ¥: установившийся или принужденный режим.
Переходный процесс закончился. В цепи установились постоянные токи и напряжения. Ветвь с конденсатором снова имеет бесконечно большое сопротивление, а индуктивность опять рассматриваем как простой проводник, без сопротивления.
Поэтому  ,
,  ,
,  .
.
4. 0 < t < ¥: переходный режим; все токи и напряжения изменяются во времени; идет перераспределение энергии между реактивными элементами; напряжение на индуктивности и ток в емкости не постоянны, а являются функциями времени, которые и требуется найти.
|
|
Законы изменения токов и напряжений в переходном режиме зависят от корней характеристического уравнения, которое записываем, руководствуясь следующими правилами:
– для послекоммутационной цепи составляем выражение комплексного входного сопротивления Z (jw) относительно разомкнутых зажимов любой ветви при мысленно закороченных ЭДС; для упрощения задачи советуем выражение Z (jw) записывать, разомкнув ветвь с конденсатором (рис. 3);
– заменяем jw на р и полученное выражение приравниваем к нулю, это и будет характеристическое уравнение:
 ,
,  :
:
 . (4)
. (4)

Рис. 3. Схема для написания характеристического уравнения
Последнее уравнение приводим к виду
 . (5)
. (5)
Точно такое же уравнение получается, если выражение Z(jw) записывать относительно разомкнутых зажимов любой другой ветви. Предлагаем учащемуся это проверить.
Рекомендуем не подставлять сразу числовые значения параметров в уравнение (4), а предварительно привести его к виду (5), то есть сначала записать приведенное квадратное уравнение в буквенных обозначениях и только потом подставлять числа. Это снизит вероятность появления арифметической ошибки при вычислении корней, а в случае ее возникновения облегчит проверку.
Во всех вариантах рассматриваемого задания корни уравнения (5) – сопряженные комплексные числа:
 .
.
В этом случае свободная составляющая тока или напряжения на любом участке представляет собой синусоиду, затухающую по экспоненциальному закону. Например, для тока i будем иметь
 . (6)
. (6)
Здесь a и w – численные значения вещественной и мнимой составляющих корней характеристического уравнения, а А и y – постоянные интегрирования, для определения которых необходимо иметь два уравнения. Получаем их следующим образом.
Дифференцируем (6):
 . (7)
. (7)
Теперь (6) и (7) записываем для момента t= 0:


В левые части этих уравнений подставляем значения тока и его производной в момент коммутации, найденные в пункте 2.
Решение последней системы довольно просто. Из уравнения (8) получим
 (10)
(10)
Подставляя это значение в (9), находим
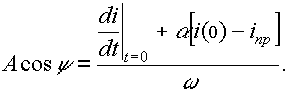 (11)
(11)
Теперь, разделив (10) на (11), получим значение тангенса угла y и сам этот угол. И, наконец, из (10) либо (11) находим А. Последнее может оказаться отрицательным, и выражение тока получится, например, таким:
|
|
 .
.
Можно его так и оставить, но лучше минус перед свободной составляющей поменять на плюс, прибавив к аргументу синуса 1800 (с плюсом или минусом):
 . (12)
. (12)
Полученное выражение следует проверить.
Подставляя в него t =0, мы должны получить найденное ранее значение i (0):

Правда, эта проверка удостоверяет только отсутствие ошибок в определении А и y из уравнений (8) и (9), но она не гарантирует правильности всех предыдущих расчетов.
Аналогично току i (t) находится ток или напряжение на любом другом участке.
Операторный метод
В основу операторного метода положен математический аппарат операционного исчисления, когда функции времени и описывающие их дифференциальные уравнения заменяются соответственно алгебраическими функциями комплексного переменного и алгебраическими уравнениями. Решения последних, так называемые изображения, позволяют по определенным правилам записывать искомые функции времени – оригиналы.
Приложение операционного исчисления к задачам электротехники привело к созданию операторного метода, вообще не требующего составления дифференциальных уравнений. Реальные электрические схемы преобразуются в чисто математические – операторные схемы, расчет которых формально не отличается от расчета обыкновенных электрических цепей.
Составление операторных схем ведется по следующим правилам:
– операторная схема сохраняет конфигурацию послекоммутационной электрической цепи;
– сопротивления переносятся в операторную схему без изменения;
– индуктивность L заменяется элементом рL, последовательно с которым включается добавочная ЭДС Li (0), направленная по току;
– емкость С заменяется элементом 1 /рC, последовательно с которым включается добавочная ЭДС uC( 0 )/р, направленная против тока;
– ЭДС и токи заменяются их изображениями (рис. 4).
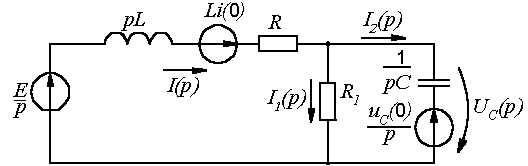
Рис. 4. Операторная схема
Полученная схема может быть рассчитана любым известным методом. Например, применение контурных токов приводит к следующим уравнениям:
 (13)
(13)
Операторные токи I(р) и I2(р) находятся из этой системы, а I 1 (р), если необходимо, по первому закону Кирхгофа в операторной форме:
|
|
I1(р)=I(р)–I2(р).
Изображение напряжения на конденсаторе определяется по закону Ома в операторной форме (рис. 4):
 . (14)
. (14)
Изображения токов из системы (13) удобнее всего находить с помощью определителей. Например, для тока I 2 (р) будем иметь:
 .
.
Раскрыв определители и упростив числитель и знаменатель в выражении I 2 (р), после проверки (как она выполняется, см. ниже) подставляем его в (14). В результате получаем выражение вида
 , (15)
, (15)
где а, b, d, f, g, h – некоторые числа.
Перед отысканием оригинала полученное изображение необходимо проверить с помощью предельных соотношений операционного исчисления:
1.  ,3)
,3) 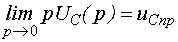 ,
,
2.  ,4)
,4)  .
.
По этим же формулам делается и упомянутая выше проверка тока I2(р).
Если задача имеет нулевые начальные условия, т.е. iL (0)=0 и uC (0)=0, что имеет место при подключении к источнику цепи с незаряженным конденсатором, как например на рис. 5, а, то операторная схема не содержит добавочных ЭДС (рис. 5, б), и для расчета можно использовать закон Ома:
 ,
,
 и т.д.
и т.д.

Рис. 5. Электрическая (а) и операторная (б) схемы с нулевыми начальными условиями
Приступаем к отысканию оригинала uC(t) по его изображению UC(р).
Так как знаменатель в формуле (15) имеет нулевой корень, используем следующую формулу разложения:
 . (16)
. (16)
Применение формулы покажем на конкретном числовом примере.
Предположим, что в результате всех проделанных вычислений мы получили следующее выражение:
 .
.
Для упрощения дальнейших выкладок рекомендуем разделить все члены дроби на коэффициент при р 2 знаменателя, т.е. на 4 · 10-4:
 . (17)
. (17)
В формуле разложения F 1 (р) и F 2 (р) – это полиномы, стоящие в числителе и знаменателе изображения:
F 1(р) = 1050 р 2 + 512000 р+ 1375 · 106,
F 2(р) =р 2 + 750 р+ 1,375 · 106.
Записываем их значения при р = 0:
F 1(0) = 1375 · 106, F 2(0) = 1,375 · 106.
Далее находим корни полинома – знаменателя, т.е. решаем уравнение F 2 (р)= 0:
р 2 + 750 р+ 1,375 · 106 = 0,
 .
.
Эти значения должны совпадать с корнями характеристического уравнения в классическом методе.
Примем: р 1 = – 375 +j 1111 = 1173 е j 108,7°,
р 2 = – 375– j 1111 = 1173 е– j 108,7°.
Найденные корни подставляем вместо р в числитель изображения UС (р), т.е. вычисляем F 1(р 1) и F 1(р 2):
F 1(р 1) =1050(-375+ j 1111)2+512000(-375+ j 1111)+1375 · 106=
=(34,62- j 306,1) · 106=308 · 106 е – j 83,5°,
F 1(р 2) =1050(-375- j 1111)2+512000(-375- j 1111)+1375 · 106=308 · 106 е j 83,5°.
Теперь дифференцируем полином, стоящий в скобках в знаменателе формулы (17), т.е. находим F 2? (р) = 2 р+ 750 и вычисляем его значения при
р =р 1 и р =р 2 :
F 2 (р 1) =2(-375+ j 1111)+750=1111· 2 j,
F 2 (р 2) =2(-375- j 1111)+750= -1111· 2 j.
Результат записываем именно в такой форме, выделяя в нем множитель 2 j.
Обращаем внимание на то, что каждая пара результатов в проведенных вычислениях – это сопряженные комплексные числа.
Подставляем найденные величины в формулу разложения (16):
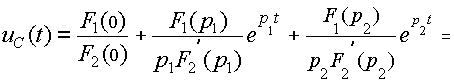

 .
.
Второе и третье слагаемые объединяем в одну дробь, вынося общие множители и собирая вместе соответствующие экспоненты:
|
|
 .
.
Вторая дробь в соответствии с формулой Эйлера

представляет собой синус выражения, стоящего в показателе степени экспоненты:
uC (t) =1000+236,3 e –375 tsin (1111 t -192,2°).
или
uC (t) =1000+236,3 e –375 tsin (1111 t +167,8°),
Подставляя сюда t= 0 и t ® ¥, проверяем соответствие полученного выражения моменту коммутации и установившемуся режиму:
 ,
,
 .
.
Определение тока в ЕМКОСТИ
Ток, протекающий через конденсатор (ток i2 в заданной схеме), можно рассчитать классическим или операторным методами (см. разд. 1, 2). Но если закон изменения напряжения на конденсаторе известен, его можно найти из уравнения
 . (19)
. (19)
Именно так и требуется сделать в настоящей работе.
После взятия производной от uC (t) приходится искать сумму
вида a sin (w t+y) + b cos (w t+y), которая легко находится символическим методом.
Например, при С = 4 мкФ применение формулы (19) к полученной ранее функции uC (t) приведет к выражению
i2 (t) = e -375 t [-0,354 sin (1111 t+ 167,8°) + 1,05 cos (1111 t+ 167,8°)].
Синус и косинус в квадратных скобках заменяем соответствующими им комплексными числами, учитывая, что cos (1111 t+ 167,8°) = sin (1111 t+ 257,8°), производим следующие вычисления:
-0,354 е j 167,8° +1,05 e j 257,8° = 0,346- j 0,0748+(-0,222- j 1,026)=
=0,124- j 1,10=1,11 e – j 83,6°.
Делаем обратный переход к синусоидальной функции времени:
i2 (t)=1,11 e –375 t sin (1111 t- 83,6°). (20)
При t =0 выражение (20) должно дать число, равное значению i2 (0), найденному в п. 2 разд. 1.
 .
.
МЕТОД ПЕРЕМЕННЫХ СОСТОЯНИЯ
|
|
|

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!