ТЕОРИЯ И ПРАКТИКА
Рекомендовано редакционно-издательским советом университета
в качестве учебного пособия для студентов специальностей
220301, 230104, 230201 очной формы обучения
Кострома
ИЗДАТЕЛЬСТВО

УДК 519.22 (075)
З 51
Рецензенты: кафедра математических методов в экономике
Костромского государственного университета им. Н.А. Некрасова;
канд. физ.-мат. наук, доцент кафедры математического анализа
Костромского государственного университета им. Н.А. Некрасова К.Е. Ширяев.
З 51 Землякова, И.В. Математическая статистика. Теория и практика: учебное пособие / И.В. Землякова, О.Б. Садовская, А.В. Чередникова. – Кострома: Изд-во Костром. гос. технол. ун-та, 2010. – 60 с.
ISBN 978-5-8285-0525-8
Учебное пособие содержит в максимально доступной форме теоретический материал, примеры, тесты и прокомментированный алгоритм выполнения заданий по типовому расчету.
Предназначено для студентов вузов, обучающихся по специальностям 220301, 230104, 230201 очной формы обучения. Может использоваться как во время лекций, так и на практических занятиях.
УДК 519.22 (075)
ISBN 978-5-8285-0525-8
 ÓКостромской государственный технологический университет, 2010
ÓКостромской государственный технологический университет, 2010
ОГЛАВЛЕНИЕ
§1. Задачи математической статистики. 4
§2. Генеральная и выборочная совокупность. Репрезентативность выборки.
Способы отбора (способы организации выборки) 4
§3. Статистическое распределение выборки. Графическое представление
распределений. 6
§4. Статистические оценки параметров распределения. 18
§5. Генеральная средняя. Выборочная средняя. Оценка генеральной
средней по выборочной средней. 20
§6. Генеральная дисперсия. Выборочная дисперсия. Оценка генеральной
дисперсии по исправленной дисперсии. 22
§7. Метод моментов и метод наибольшего правдоподобия нахождения
оценок параметров. Метод моментов. 25
§8. Доверительная вероятность. Доверительный интервал. 27
§9. Проверка гипотезы о соответствии статистических данных
теоретическому закону распределения. 32
§ 10. Понятие о корреляционном и регрессивном анализе. 39
Индивидуальные задания. 44
Ответы и указания. 46
Приложения. 51
ГЕНЕРАЛЬНАЯ И ВЫБОРОЧНАЯ СОВОКУПНОСТЬ.
СТАТИСТИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ ВЫБОРКИ.
Таблица 1
| Варианта xi
| x1
| x2
| …
| xk
|
| Частота ni
| n1
| n2
| …
| nk
|
Таблицу 1 называют дискретным статистическим рядом распределения (ДСР) частот, или таблицей частот.
Таблица 2
| Варианта xi
| x1
| x2
| …
| xk
|
| Относительная частота wi
| w1
| w2
| …
| wk
|
Таблица 2 - ДСР относительных частот, или таблица относительных частот.
: Определение. Модой называется наиболее часто встречающийся вариант, т.е. вариант с наибольшей частотой. Обозначается xмод .
: Определение. Медианой называется такое значение признака, которое делит всю статистическую совокупность, представленную в виде вариационного ряда, на две равных по числу части. Обозначается  .
.
Если n нечетно, т.е. n = 2m + 1, то  = xm+1.
= xm+1.
Если n четно, т.е. n = 2m, то  .
.
Пример 3. По результатам наблюдений: 1, 7, 7, 2, 3, 2, 5, 5, 4, 6, 3, 4, 3, 5, 6, 6, 5, 5, 4, 4 построить ДСР относительных частот. Найти моду и медиану.
Решение. Объем выборки n = 20. Составим ранжированный ряд элементов выборки: 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6, 6, 6, 7, 7. Выделим варианты и подсчитаем их частоты (в скобках): 1 (1), 2 (2), 3 (3),
4 (4), 5 (5), 6 (3), 7 (2). Строим таблицу:
| xi
|
|
|
|
|
|
|
|
| wi
| 1/20
| 2/20
| 3/20
| 4/20
| 5/20
| 3/20
| 2/20
|
Наиболее часто встречающийся вариант xi = 5. Следовательно, xмод = 5. Так как объем выборки n – четное число, то 
Если на плоскости нанести точки  и соединить их отрезками прямых, то получим полигон частот.
и соединить их отрезками прямых, то получим полигон частот.
Если на плоскости нанести точки 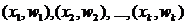 , то получим полигон относительных частот.
, то получим полигон относительных частот.
Пример 4. Построить полигон частот и полигон относительных частот по данному распределению выборки:
| xi
|
|
|
|
|
|
| ni
|
|
|
|
|
|
| wi
| 2/20
| 4/20
| 5/20
| 6/20
| 3/20
|
Решение. На рисунке 2 показан полигон частот и на рисунке 3 – полигон относительных частот.


Рис. 2 Рис. 3
Замечание. Чем круче полигон, тем равномернее процесс.
II. Пусть количественный признак X – непрерывная случайная величина, принимающая значения из интервала (а,b). Весь диапазон наблюдаемых данных делят на частичные интервалы [ хi; xi+1), которые берут обычно одинаковыми по длине:  = xi+1 – xi (i = 0, 1, …, k). Для определения величины интервала
= xi+1 – xi (i = 0, 1, …, k). Для определения величины интервала  можно использовать формулу Стерджеса:
можно использовать формулу Стерджеса:

где (xmax – xmin)- разность между наибольшим и наименьшим значениями признака, k = 1 + log2 n - число интервалов (log2 n» 3,322 lg n). Если окажется, что h - дробное число, то за длину частичного интервала следует брать либо ближайшее целое число, либо ближайшую простую дробь. За начало первого интервала рекомендуется брать величину x нач = x min –  . В каждом из частичных интервалов подсчитывают число наблюдаемых значений, т.е. частоту ni. По частотам находят относительные частоты
. В каждом из частичных интервалов подсчитывают число наблюдаемых значений, т.е. частоту ni. По частотам находят относительные частоты 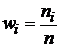 . Полученные интервалы и соответствующие им частоты (или относительные частоты) записывают в виде таблицы 3. При этом правая граница последнего интервала тоже включается.
. Полученные интервалы и соответствующие им частоты (или относительные частоты) записывают в виде таблицы 3. При этом правая граница последнего интервала тоже включается.
Таблица 3
| Частичный интервал [ xi,xi+1)
| [ x0, x1)
| [ x1, x2)
| …
| [ xk-1, xk ]
|
| Относительная частота wi
| w1
| w2
| …
| wk
|
Таблица 3 называется интервальным статистическим рядом распределения (ИСР) относительных частот, который задаёт распределение выборки. Аналогично составляется ИСР частот.
Пример 5. Измерили рост (с точностью до см) 30 наудачу отобранных студентов. Результаты измерений таковы:
178, 160, 154, 183, 155, 153, 167, 186, 163, 155, 157, 175, 170, 166, 159,
173, 182, 167, 171, 169, 179, 165, 156, 179, 158, 171, 175, 173, 164, 172.
Построить интервальный статистический ряд относительных частот.
Решение. Для удобства проранжируем полученные данные:
153, 154, 155, 155, 156, 157, 158, 159, 160, 163, 164, 165, 166, 167, 167,
169, 170, 171, 171, 172, 173, 173, 175, 175, 178, 179, 179, 182, 183, 186.
Отметим, что Х - рост студента - непрерывная случайная величина. Как видим, xmin = 153, хmax = 186; по формуле Стерджеса, при n = 30, находим длину частичного интервала

Примем  = 6. Тогда хнач = 153 –
= 6. Тогда хнач = 153 –  =150. Исходные данные разбиваем на шесть (k = 1 + log230 = 5,907» 6) интервалов:
=150. Исходные данные разбиваем на шесть (k = 1 + log230 = 5,907» 6) интервалов:
[150, 156), [156, 162), [162, 168), [168, 174), [174, 180), [180, 186].
Подсчитав число студентов ni, попавших в каждый из полученных промежутков, получим ИСР:
| [ xi,xi+1)
| [150, 156)
| [156, 162)
| [162, 168)
| [168, 174)
| [174,180)
| [180,186]
|
| ni
|
|
|
|
|
|
|
| w i
| 4/30
| 5/30
| 6/30
| 7/30
| 5/30
| 3/30
|
Первая и третья строчка таблицы образует ИСР относительных частот.
Замечание. При решении учебных задач на построение ИСР можно пользоваться следующими правилами.
1. Назначаются нижняя граница а и верхняя граница b для вариант так, чтобы отрезок [ a; b ] вместил всю выборку; часто полагают 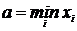 ,
,  , но иногда a и b назначают из соображений удобства, но не слишком далеко от
, но иногда a и b назначают из соображений удобства, но не слишком далеко от  и
и  .
.
2. Находится число k равных по длине частичных интервалов варьирования, которое зависит от объема выборки и обычно 6 £ k £ 20; рассчитывается длина интервалов группирования  .
.
Интервальный статистический ряд распределения, представленный графически, называется гистограммой.
Гистограмма относительных частот строится следующим образом: по оси абсцисс откладываются интервалы (хi; хi+1) и на каждом из них строится прямоугольник высотой

где  ;
;  .
.
Площадь i- го прямоугольника  .
.
Площадь всей гистограммы  .
.
 Замечание: гистограмма на рисунке 4 – гистограмма относительных частот.
Замечание: гистограмма на рисунке 4 – гистограмма относительных частот.

Рис. 4
Можно построить гистограмму частот, высоты прямоугольников которых равны  .
.
Пример 6. Построить гистограмму частот по данному ИСР частот:
| [ xi; xi +1)
| [100; 120)
| [120; 140)
| [140; 160)
| [160; 180)
| [180; 200]
|
| ni
|
|
|
|
|
|
Решение. По ИСР частот находим длину частичных интервалов
 = 20 и высоты прямоугольников hi =
= 20 и высоты прямоугольников hi =  . Результаты занесем в таблицу:
. Результаты занесем в таблицу:
| [ xi; xi +1)
| [100; 120)
| [120; 140)
| [140; 160)
| [160; 180)
| [180; 200]
|
| ni
|
|
|
|
|
|
| hi
|
| 2,5
|
|
| 0,5
|
Искомая гистограмма частот изображена на рис. 5.

Рис. 5
В теории вероятностей гистограмме относительных частот соответствует график плотности распределения вероятностей. Распределение выборки, задаваемое интервальным статистическим рядом (табл. 3) или таблицей относительных частот (табл. 2), называется эмпирическим распределением случайной величины.
По теореме Бернулли относительная частота wi, появление события в п независимых испытаниях сходится по вероятности к вероятности рi этого события  . Значит во второй строке таблицы 3 и таблицы 2 стоят приближённые значения вероятностей рi следующих событий
. Значит во второй строке таблицы 3 и таблицы 2 стоят приближённые значения вероятностей рi следующих событий  и
и  , поэтому распределение выборки называют эмпирическим распределением случайной величины X.
, поэтому распределение выборки называют эмпирическим распределением случайной величины X.
Замечания.
1. Выборочные средние, найденные по нескольким выборкам достаточно большого объёма из некоторой генеральной совокупности, приближенно равны между собой.
2. Предполагали, что выборка повторная. Однако полученные выводы применимы и для бесповторной выборки, если её объём значительно меньше объема генеральной совокупности.
3. Эффективность или неэффективность зависит от вида закона распределения признака X. Если X распределена по нормальному закону, то  будет минимально возможной, т.е. средняя выборочная является эффективной оценкой.
будет минимально возможной, т.е. средняя выборочная является эффективной оценкой.
Решение.
 ;
;  .
. 
 – доверительный интервал.
– доверительный интервал.
Если, например,  , то (3,12; 5,08).
, то (3,12; 5,08).
Смысл результата: если произведено достаточно большое число выборок, то 95% из них определяют такие доверительные интервалы, в которых неизвестное математическое ожидание а действительно заключено. Лишь в 5% случаев а может выйти за границы доверительного интервала.
Вычисление объема выборки при заданных  и
и 
Пусть требуется оценить математическое ожидание, если заданы доверительная вероятность  и точность оценки
и точность оценки  .
.
Точность оценки  . Тогда
. Тогда  .
.
Значит,  – минимальный объем выборки, который обеспечит заданную точность
– минимальный объем выборки, который обеспечит заданную точность  .
.
Замечание. Доверительный интервал для оценки математического ожидания нормального распределения при неизвестном 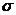 .
.
X – количественный признак, распределён нормально. a, 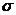 – неизвестны.
– неизвестны.
Требуется оценить a.
Можно доказать, что  - доверительный интервал, покрывающий неизвестное математическое ожидание a с доверительной вероятностью
- доверительный интервал, покрывающий неизвестное математическое ожидание a с доверительной вероятностью  , где
, где 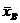 – выборочная средняя;
– выборочная средняя; 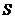 – исправленное среднее квадратическое отклонение;
– исправленное среднее квадратическое отклонение;  – квантиль распределения, который находят по таблице 3 по заданным
– квантиль распределения, который находят по таблице 3 по заданным 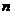 и
и  .
.
Задачи _______________________________________________________ ´
1. Найти доверительный интервал для оценки с надежностью 0,99 неизвестного математического ожидания a нормально распределённого признака Х генеральной совокупности, если известны генеральное среднее квадратичное отклонение σ = 4, выборочная средняя  и объём выборки n = 16.
и объём выборки n = 16.
2. На овцеводческой ферме из стада произведена выборка для взвешивания 36 овец. Их средний вес оказался равным 50 кг. Предположив распределение веса нормальным и определив несмещённую оценку выборочной дисперсии S 2 = 16, найти доверительный интервал для оценки математического ожидания с надёжностью 0,95.
3. Выборка из большой партии электроламп содержит 100 ламп. Средняя продолжительность горения лампы выборки оказалась равной 1000 ч. Найти с надежностью 0,95 доверительный интервал для средней продолжительности a горения лампы всей партии, если известно, что продолжительность горения лампы распределена нормально.
4. Найти минимальный объём выборки, при котором с надежностью 0,975 точность оценки математического ожидания a генеральной совокупности по выборочной средней равна δ = 0,3, если известно среднее квадратичное отклонение σ = 1,2 нормально распределённой генеральной совокупности.
5. Найти минимальный объем выборки, при котором с надежностью 0,925 точность оценки математического ожидания нормально распределённой генеральной совокупности по выборочной средней равна 0,2, если известно среднее квадратичное отклонение генеральной совокупности σ = 1,5.
6. Из генеральной совокупности извлечена выборка:
Оценить с надежностью 0,95 математическое ожидание a нормально распределённого признака генеральной совокупности по выборочной средней при помощи доверительного интервала.
7. Из генеральной совокупности извлечена выборка:
| xi
| -0,5
| -0,4
| -0,2
|
| 0,2
| 0,6
| 0,8
|
| 1,2
| 1,5
|
| ni
|
|
|
|
|
|
|
|
|
|
|
Оценить с надежностью 0,95 математическое ожидание a нормально распределённого признака генеральной совокупности по выборочной средней при помощи доверительного интервала.
8. По данным выборки объёма n = 50 из генеральной совокупности нормально распределённого количественного признака найдено исправленное среднее квадратичное отклонение s = 14. Найти доверительный интервал, покрывающий генеральное среднее квадратичное отклонение σ с надежностью 0,999.
9. Случайная величина Х распределена по нормальному закону. Статистическое распределение выборки представлено в таблице:
Найти с надежностью 0,97 доверительный интервал для оценки математического ожидания и с надежностью 0,95 – для оценки среднего квадратичного отклонения.
10. Случайная величина Х распределена по нормальному закону. Статистическое распределение выборки представлено в таблице:
Найти с надежностью 0,95 доверительный интервал для оценки математического ожидания и с надежностью 0,99 – для оценки среднего квадратичного отклонения.
§9. ПРОВЕРКА ГИПОТЕЗЫ О СООТВЕТСТВИИ
СТАТИСТИЧЕСКИХ ДАННЫХ
ТЕОРЕТИЧЕСКОМУ ЗАКОНУ РАСПРЕДЕЛЕНИЯ
Предположение о том, что статистические данные о количественном признаке Х соответствуют теоретическому закону распределения (назовём его А), является статистической гипотезой, обозначаемой чаще всего через Н  . Ставится задача – проанализировав экспериментально полученные данные, обосновать выбор одного из двух решений:
. Ставится задача – проанализировав экспериментально полученные данные, обосновать выбор одного из двух решений:
1) принять гипотезу о распределении статистических данных по закону А;
2) отвергнуть гипотезу о соответствии данных выборки закону распределения А.
В силу того, что данные выборки случайны, нет гарантии, что принятое решение будет правильным. Возможны два варианта ошибок:
1) ошибка 1-го рода – отвергнута правильная гипотеза;
2) ошибка 2-го рода – принята неправильная гипотеза.
Всю ситуацию можно описать таблицей 4
Таблица 4
| Решение
| Гипотеза
|
| правильная
| неправильная
|
| Принять гипотезу
| Нет ошибки
| Ошибка 2-го рода
|
| Отвергнуть гипотезу
| Ошибка 1-го рода
| Нет ошибки
|
Вероятность совершить ошибку 1-го рода называют уровнем значимости гипотезы и обозначают a. Величину a задают такой, чтобы случайное событие с вероятностью a можно было считать практически невозможным. Обычно используют значения a, равные 0,01; 0,05; 0,1. Для проверки статистических гипотез используют специально подобранные случайные величины, оценивающие степень расхождения эмпирического и теоретического законов, называемые критериями. Таким образом, гипотеза Н  – есть предположение о характере распределения признака Х, а используемый для проверки критерий называют критерием согласия. Выбор теоретического закона распределения А обычно выполняется по гистограмме интервального статистического ряда на основании соответствия её плотности распределения закону А. Наиболее часто выбирается нормальный закон распределения, и для проверки соответствия ему опытных данных используются критерии согласия Пирсона, Ястремского, Колмогорова, Вилкоксона.
– есть предположение о характере распределения признака Х, а используемый для проверки критерий называют критерием согласия. Выбор теоретического закона распределения А обычно выполняется по гистограмме интервального статистического ряда на основании соответствия её плотности распределения закону А. Наиболее часто выбирается нормальный закон распределения, и для проверки соответствия ему опытных данных используются критерии согласия Пирсона, Ястремского, Колмогорова, Вилкоксона.
Опишем процедуру проверки гипотезы о соответствии экспериментальных данных нормальному закону распределения по критерию согласия Пирсона.
1. Примем определённое значение уровня значимости a.
2. Сгруппируем экспериментальные данные в классы (интервалы) таким образом, чтобы в каждый класс попало не менее пяти наблюдений. Число, полученных классов обозначим k. Для расчёта числа классов без учёта объединения существует несколько формул, например
к» 1 + 3,2 lg n, где n – объем выборки.
3. Найдём статические оценки параметров нормального распределения:
a 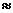
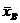 и
и  S
S  .
.
4. Найдём для каждого класса (xi, xi+1) выровненные частоты  =Рi× n, где n – объём выборки; Ф(х) – функция Лапласа:
=Рi× n, где n – объём выборки; Ф(х) – функция Лапласа:
(11)
5. В качестве критерия согласия рассмотрим случайную величину, обозначаемую c2 и определяемую по формуле:
(12)
Случайная величина Пирсона c2 имеет специальное распределение, зависящее от числа степеней свободы r. Для гипотезы о нормальном распределении Х, число степеней свободы:
r = k – 3, где k – число классов. (13)
Очевидно, что чем ближе эмпирические частоты ni к теоретическим (выровненным) частотам  , тем более достоверна гипотеза о нормальном распределении, и в то же время тем меньше значение c2.
, тем более достоверна гипотеза о нормальном распределении, и в то же время тем меньше значение c2.
На рисунке 7 изображён график плотности распределения c2 (дифференциальной функции f (c2)) для r = 6. Вся площадь между графиком и осью абсциссравна единице. Незаштрихованная часть площади равна вероятности  , заштрихованная площадь равна вероятности
, заштрихованная площадь равна вероятности  .
.
Рис. 7
Пусть заштрихованная площадь равна уровню значимости:
 (16)
(16)
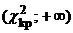 где a – вероятность практически невозможного события. Тогда попадание c2 в интервал практически невозможно. Заштрихованную площадь называют критической областью данного уровня значимости.
где a – вероятность практически невозможного события. Тогда попадание c2 в интервал практически невозможно. Заштрихованную площадь называют критической областью данного уровня значимости.
Очевидно, что чем больше a, тем меньшим (при данном числе степеней свободы r) будет значение  . Имеются таблицы распределения
. Имеются таблицы распределения  (Пирсона), в которых приведены значения
(Пирсона), в которых приведены значения  для различного числа степеней свободы r и уровней значимости a. При одном и том же уровне значимости a значение
для различного числа степеней свободы r и уровней значимости a. При одном и том же уровне значимости a значение  возрастает при увеличении числа степеней свободы r.
возрастает при увеличении числа степеней свободы r.
6. Определяем значение  для принятого уровня значимости и числа степеней свободы r.
для принятого уровня значимости и числа степеней свободы r.
7. По данным статистического ряда вычисляем наблюдаемое (в данной выборке) значение  . Обозначим это значение
. Обозначим это значение
(15)
8. Сравнивая  и
и  решаем вопрос о принятии или отклонении гипотезы Н
решаем вопрос о принятии или отклонении гипотезы Н  о соответствии данных выборки нормальному закону распределения, исходя из следующего:
о соответствии данных выборки нормальному закону распределения, исходя из следующего:
– если  >
>  , то это означает, что наблюдаемое значение попало в критическую область, т.е. произошло событие, которое считали практически невозможным. Следовательно, данные выборки противоречат гипотезе о нормальном распределении, и гипотеза отвергается;
, то это означает, что наблюдаемое значение попало в критическую область, т.е. произошло событие, которое считали практически невозможным. Следовательно, данные выборки противоречат гипотезе о нормальном распределении, и гипотеза отвергается;
– если 
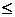
 , то это означает, что данные выборки не противоречат гипотезе о нормальном распределении, гипотезу можно принять.
, то это означает, что данные выборки не противоречат гипотезе о нормальном распределении, гипотезу можно принять.
Пример 11. Проверка по критерию Пирсона гипотезы о нормальном распределении количественного признака Х по результатам 150 его измерений, сведённых в таблицу частот:
| Границы интервала
(x i - x i+1)
| Частота
n i
| Относительная частота w i
| Середина интервала
x* i
|
| 24,5–27,5
|
| 0,0067
|
|
| 27,5–30,5
|
| 0,0267
|
|
| 30,5–33,5
|
| 0,0867
|
|
| 33,5–36,5
|
| 0,1533
|
|
| 36,5–39,5
|
| 0,1467
|
|
| 39,5–42,5
|
| 0,1933
|
|
| 42,5–45,5
|
| 0,1933
|
|
| 45,5–48,5
|
| 0,1067
|
|
| 48,5–51,5
|
| 0,0733
|
|
| 51,5–54,5
|
| 0,0133
|
|
Построим гистограмму, где по оси абсцисс отложим отрезки [xi; xi+1],
а hi=Wi/Dxi=Wi/3.

По форме гистограммы выдвинем гипотезу Н  : изучаемый признак Х имеет нормальный закон распределения. Найдём оценки числовых характеристик закона:
: изучаемый признак Х имеет нормальный закон распределения. Найдём оценки числовых характеристик закона:
- выборочные средняя и дисперсия: 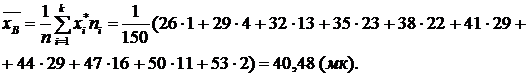
 - исправленное среднее квадратичное отклонение:
- исправленное среднее квадратичное отклонение:

Вычисляем значения аргумента  и значения функции Лапласа (по таблице значений функции Лапласа) в этих точках.
и значения функции Лапласа (по таблице значений функции Лапласа) в этих точках.
Приведём вычисления для первого и последнего классов.




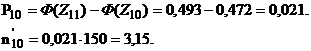
Для остальных классов выравненные относительные частоты Pi и выравненные частоты  определяются аналогично.
определяются аналогично.
Выравненные частоты для укрупненных классов приведены в таблице
| Границы интервала
xi-xi+1
| Частота
ni
| Относительная частота
wi
| Выравненная относительная частота
Pi
| Выравненная частота
n i'= Pi ×150
| 
|
| 24,5–27,5
| 
| 0,0067
| 
| 
| 0,12
|
| 27,5–30,5
| 0,0267
|
| 30,5–33,5
|
| 0,0867
| 0,0711
| 10,67
| 0,51
|
| 33,5–39,5
|
| 0,1533
| 0,1308
| 19,62
| 0,58
|
| 36,5–39,5
|
| 0,1467
| 0,1905
| 28,58
| 1,57
|
| 39,5–42,5
|
| 0,1933
| 0,2043
| 30,65
| 0,09
|
| 42,5–45,5
|
| 0,1933
| 0,1738
| 26,07
| 0,33
|
| 45,5–48,5
|
| 0,1067
| 0,1086
| 16,29
| 0,1
|
| 48,5–51,5
| 
| 0,0733
| 
| 
|
0,031
|
| 51,5–54,5
| 0,0133
|
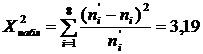
Примечание. Два первых класса и два последних класса объединены ввиду их малочисленности.
Этапы реализации критерия Пирсона:
1. Примем уровень значимости a = 0,05.
2. Сгруппируем классы так, чтобы частота в каждом классе была не менее пяти. Для этого объединим два первых класса и объединим два последних класса. При этом частоты ni и выравненные частоты ni’ для объединенных классов суммируются. Число классов стало k = 8. В каждом классе подсчитываем величину  .
.

 3. Из таблицы критических точек распределения (см. приложение 6) найдем для числа степеней свободы r = 8 – 3 = 5 и принятого уровня значимости a = 0,05. Получим
3. Из таблицы критических точек распределения (см. приложение 6) найдем для числа степеней свободы r = 8 – 3 = 5 и принятого уровня значимости a = 0,05. Получим  .
.
4. По последней таблице подсчитываем наблюдаемое значение критерия

5. Сравним  и
и  .
.
Так как  , то гипотезу о нормальном распределении можно считать правдоподобной.
, то гипотезу о нормальном распределении можно считать правдоподобной.
Задачи _______________________________________________________ ´
1. Результаты взвешивания 50 случайным образом отобранных пачек чая приведены ниже (в граммах):
150; 147; 152; 148; 149; 153; 151; 150; 149; 147; 153; 151; 152; 151; 149; 152; 150; 148; 152; 150; 152; 151; 148; 151; 152; 150; 151; 149; 148; 149; 150; 150; 151; 149; 151; 150; 151; 150; 149; 148; 147; 153; 147; 152; 150; 151; 149; 150; 151; 153.
Можно ли утверждать при уровне значимости α = 0,05, что случайная величина X – масса пачки чая – подчинена нормальному закону распределения?
2. Масса (в граммах) произвольно выбранных 30 пачек полуфабриката «Геркулес» такова: 503; 509; 495; 493; 489; 485; 507; 511; 487; 495; 506; 504; 507; 511; 499; 491; 494; 518; 506; 515; 487; 509; 507; 488; 495; 490; 498; 497; 492; 495.
Можно ли при уровне значимости α = 0,05 утверждать, что случайная величина X – масса пачки – подчинена нормальному закону распределения?
3. Результаты исследования числа покупателей в универсаме, в зависимости от времени работы, приведены ниже:
| Часы работы
| [9; 10)
| [10; 11)
| [11; 12)
| [12; 13]
|
| Число покупателей
|
|
|
|
|
Можно ли утверждать при уровне значимости α = 0,05, что случайная величина X – число покупателей – подчинена нормальному закону распределения?
4. При обследовании диаметров карданных валов автомобиля, выпускаемых заводом, были зафиксированы отклонения от номинала Δ d (мкм), приведенные в таблице:
| -8,760
| -1,455
| -1,455
| -4,665
| -2,250
| 2,560
| -1,645
| 0,425
| 0,650
| -1,220
|
| -6,280
| 8,550
| 3,170
| 0,360
| 2,450
| 1,590
| -5,435
| 4,495
| 5,140
| -6,520
|
| 7,655
| -2,215
| 7,045
| 8,650
| -1,660
| 1-745
| -1,460
| -4,415
| -0,280
| 3,785
|
| -4,790
| 1,240
| -0,475
| -7,440
| -1,805
| -0,295
| -2,695
| -0,390
| 1,145
| 0,970
|
| 2,075
| -6,910
| 0,645
| -11,805
| -5,435
| -5,420
| 1,590
| 1,835
| -4,960
| 2,645
|
Проверить гипотезу о нормальном распределении случайной величины Δ d при уровне доверия g = 0,9.
5. Интервал движения поездов метро составляет 2 минуты. В таблице приведены значения случайной величины X – времени ожидания пассажирами поезда:
| 0,000
| 0,002
| 0,007
| 0,025
| 0,089
| 0,312
| 1,068
| 1,604
| 0,014
| 0,045
|
| 1,747
| 1,677
| 0,341
| 0,952
| 0,945
| 1,297
| 1,981
| 0,214
| 1,452
| 0,787
|
| 1,954
| 0,838
| 0,143
| 1,317
| 0,618
| 1,853
| 1,555
| 0,953
| 1,922
| 1,653
|
| 0,617
| 0,828
| 1,413
| 1,030
| 1,459
| 1,483
| 1,769
| 1,265
| 1,669
| 0,635
|
| 0,787
| 1,004
| 0,941
| 0,612
| 1,200
| 1,692
| 1,356
| 0,908
| 1,245
| 1,295
|
Проверить гипотезу о нормальном распределении случайной величины X при уровне значимости α = 0,01.
6. По данным выборочного обследования получено распределение семей по среднедушевому доходу (в усл. ед.):
| 10,984
| 22,672
| 17,536
| 21,400
| 29,096
| 22,368
| 25,680
| 26,040
| 23,048
| 17,944
|
| 14,952
| 38,608
| 30,072
| 25,576
| 28,920
| 27,544
| 16,304
| 32,192
| 33,224
| 14,568
|
| 37,248
| 21,456
| 36,272
| 38,540
| 22,872
| 27,792
| 22,664
| 17,936
| 24,552
| 31,056
|
| 17,336
| 26,984
| 24,240
| 13,096
| 22,112
| 24,528
| 20,688
| 24,376
| 26,832
| 26,552
|
| 28,320
| 13,944
| 26,032
| 6,112
| 16,304
| 16,328
| 27,936
| 17,064
| 27,544
| 29,232
|
Проверить гипотезу о нормальном распределении случайной величины  – среднедушевого дохода семьи – при уровне доверия g = 0,9.
– среднедушевого дохода семьи – при уровне доверия g = 0,9.
7. В таблице приведены значения прибыли 50 фирм, принадлежащих одной корпорации, Q (1000 усл. ед.):
| 4,744
| 9,127
| 7,201
| 8,650
| 11,536
| 9,013
| 10,255
| 10,390
| 9,268
| 7,354
|
| 6,232
| 15,103,
| 11,902
| 10,216
| 11,470
| 10,954
| 6,739
| 12,697
| 13,084
| 6,088
|
| 14,593
| 8,671
| 14,227
| 15,190
| 9,202
| 11,047
| 9,124
| 7,351
| 9,832
| 12,271
|
| 7,126
| 10,744
| 9,715
| 5,536
| 8,917
| 9,823
| 8,383
| 9,766
| 10,687
| 10,582
|
| 11,245
| 5,854
| 10,387
| 2,917
| 6,739
| 6,748
| 10,954
| 11,101
| 7,024
| 11,587
|
Проверить гипотезу о нормальности распределения случайной величины Q при уровне доверия g = 0,99.
8. Имеются данные о годовой мощности М (тыс. т) предприятия цементной промышленности:
| 11,240
| 18,545
| 15,335
| 17,750
| 22,560
| 18,355
| 20,425
| 20,650
| 18,780
| 15,590
|
| 13,720
| 28,505
| 23,170
| 20,360
| 22,450
| 21,590
| 14,565
| 24,495
| 25,140
| 13,400
|
| 27,655
| 17,785
| 27,045
| 28,650
|




 ÓКостромской государственный технологический университет, 2010
ÓКостромской государственный технологический университет, 2010 .
. .
.
 и соединить их отрезками прямых, то получим полигон частот.
и соединить их отрезками прямых, то получим полигон частот.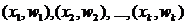 , то получим полигон относительных частот.
, то получим полигон относительных частот.

 = xi+1 – xi (i = 0, 1, …, k). Для определения величины интервала
= xi+1 – xi (i = 0, 1, …, k). Для определения величины интервала 
 . В каждом из частичных интервалов подсчитывают число наблюдаемых значений, т.е. частоту ni. По частотам находят относительные частоты
. В каждом из частичных интервалов подсчитывают число наблюдаемых значений, т.е. частоту ni. По частотам находят относительные частоты 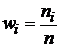 . Полученные интервалы и соответствующие им частоты (или относительные частоты) записывают в виде таблицы 3. При этом правая граница последнего интервала тоже включается.
. Полученные интервалы и соответствующие им частоты (или относительные частоты) записывают в виде таблицы 3. При этом правая граница последнего интервала тоже включается.
 = 6. Тогда хнач = 153 –
= 6. Тогда хнач = 153 –  =150. Исходные данные разбиваем на шесть (k = 1 + log230 = 5,907» 6) интервалов:
=150. Исходные данные разбиваем на шесть (k = 1 + log230 = 5,907» 6) интервалов: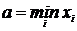 ,
,  , но иногда a и b назначают из соображений удобства, но не слишком далеко от
, но иногда a и b назначают из соображений удобства, но не слишком далеко от  и
и  .
. .
.
 ;
;  .
. .
. .
. Замечание: гистограмма на рисунке 4 – гистограмма относительных частот.
Замечание: гистограмма на рисунке 4 – гистограмма относительных частот.
 .
. . Результаты занесем в таблицу:
. Результаты занесем в таблицу:
 . Значит во второй строке таблицы 3 и таблицы 2 стоят приближённые значения вероятностей рi следующих событий
. Значит во второй строке таблицы 3 и таблицы 2 стоят приближённые значения вероятностей рi следующих событий  и
и  , поэтому распределение выборки называют эмпирическим распределением случайной величины X.
, поэтому распределение выборки называют эмпирическим распределением случайной величины X. будет минимально возможной, т.е. средняя выборочная является эффективной оценкой.
будет минимально возможной, т.е. средняя выборочная является эффективной оценкой. ;
;  .
. 
 – доверительный интервал.
– доверительный интервал. , то (3,12; 5,08).
, то (3,12; 5,08). и
и 
 . Тогда
. Тогда  .
. – минимальный объем выборки, который обеспечит заданную точность
– минимальный объем выборки, который обеспечит заданную точность 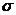 .
. - доверительный интервал, покрывающий неизвестное математическое ожидание a с доверительной вероятностью
- доверительный интервал, покрывающий неизвестное математическое ожидание a с доверительной вероятностью 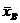 – выборочная средняя;
– выборочная средняя; 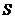 – исправленное среднее квадратическое отклонение;
– исправленное среднее квадратическое отклонение;  – квантиль распределения, который находят по таблице 3 по заданным
– квантиль распределения, который находят по таблице 3 по заданным 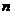 и
и  и объём выборки n = 16.
и объём выборки n = 16. . Ставится задача – проанализировав экспериментально полученные данные, обосновать выбор одного из двух решений:
. Ставится задача – проанализировав экспериментально полученные данные, обосновать выбор одного из двух решений: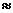
 S
S  .
. =Рi× n, где n – объём выборки; Ф(х) – функция Лапласа:
=Рi× n, где n – объём выборки; Ф(х) – функция Лапласа:

 , тем более достоверна гипотеза о нормальном распределении, и в то же время тем меньше значение c2.
, тем более достоверна гипотеза о нормальном распределении, и в то же время тем меньше значение c2. , заштрихованная площадь равна вероятности
, заштрихованная площадь равна вероятности  .
.
 (16)
(16)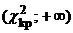 где a – вероятность практически невозможного события. Тогда попадание c2 в интервал практически невозможно. Заштрихованную площадь называют критической областью данного уровня значимости.
где a – вероятность практически невозможного события. Тогда попадание c2 в интервал практически невозможно. Заштрихованную площадь называют критической областью данного уровня значимости. . Имеются таблицы распределения
. Имеются таблицы распределения  (Пирсона), в которых приведены значения
(Пирсона), в которых приведены значения 
 и
и  решаем вопрос о принятии или отклонении гипотезы Н
решаем вопрос о принятии или отклонении гипотезы Н 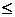

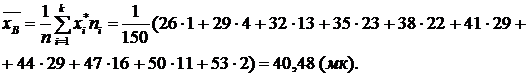
 - исправленное среднее квадратичное отклонение:
- исправленное среднее квадратичное отклонение:
 и значения функции Лапласа (по таблице значений функции Лапласа) в этих точках.
и значения функции Лапласа (по таблице значений функции Лапласа) в этих точках.



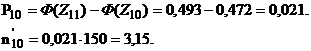
 определяются аналогично.
определяются аналогично.






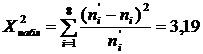
 .
.
 3. Из таблицы критических точек распределения (см. приложение 6) найдем для числа степеней свободы r = 8 – 3 = 5 и принятого уровня значимости a = 0,05. Получим
3. Из таблицы критических точек распределения (см. приложение 6) найдем для числа степеней свободы r = 8 – 3 = 5 и принятого уровня значимости a = 0,05. Получим  .
.
 и
и  .
. , то гипотезу о нормальном распределении можно считать правдоподобной.
, то гипотезу о нормальном распределении можно считать правдоподобной. – среднедушевого дохода семьи – при уровне доверия g = 0,9.
– среднедушевого дохода семьи – при уровне доверия g = 0,9.


