Общей чертой моделей излагавшихся выше подходов является то, что они описывают деятельность банка в целом, представляя его в обобщенном виде. Теперь мы остановимся на методах, ориентированных на более подробное изучение закономерностей процессов, протекающих внутри финансовых институтов. В частности, особое внимание будет уделено средствам решения задач, возникающих в ходе привлечения депозитных финансовых ресурсов.
Очевидно, что как внешние условия, сопутствующие деятельности банка (финансовой фирмы), так и процессы, протекающие внутри него, являются результатом сложных и неоднозначных взаимодействий огромного числа факторов, причин, зависимостей и закономерностей, большинство из которых имеет случайную (вероятностную) природу. Причина этого в том, что работа банков в значительной мере сопряжена с риском и неопределенностью. В связи с этим достаточно привлекательными и конструктивными представляются идеи, касающиеся использования в экономико-математических моделях банковских структур инструментального аппарата теории вероятностей, математической статистики и теории массового обслуживания.
Достаточно хорошо зарекомендовали себя в этой области методы, связанные с подходом к описанию банка как совокупности стохастических финансовых потоков.
Способы, с помощью которых может быть описано текущее состояние банка или какого-либо иного финансового института, весьма разнообразны. Однако, наверное, одним из самых логически простых и естественных будет его представление с помощью вектора состояния или, как еще говорят, вектора характеристик:
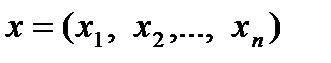 (2.5.1)
(2.5.1)
Количественный и качественный состав компонент вектора  определяется степенью детализации представления банка в модели. Это может быть, допустим, объем депозитов до востребования или же объем конкретного вклада, принадлежащего конкретному лицу.
определяется степенью детализации представления банка в модели. Это может быть, допустим, объем депозитов до востребования или же объем конкретного вклада, принадлежащего конкретному лицу.
Фактически данная форма описания состояния банка с содержательной точки зрения адекватна обычному банковскому балансу: компоненты вектора характеристик 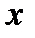 могут интерпретироваться как обычные статьи баланса, а их количество и структура соответствуют уровню его агрегированности (ежедневный, включающий счета второго порядка, или укрупненный квартальный).
могут интерпретироваться как обычные статьи баланса, а их количество и структура соответствуют уровню его агрегированности (ежедневный, включающий счета второго порядка, или укрупненный квартальный).
Конкретные значения каждой из компонент  вектора состояния определяются выбором единиц измерения для соответствующего ресурса (характеристики). Очевидно, что в подавляющем большинстве случаев это денежные измерители в той или иной валюте, но, в принципе, возможны и иные формы учета. Например, через перечисление видов, количество и номиналы облигаций или же через указание числа мерных слитков, веса драгоценных камней и т. п. Для обобщения допустимых способов исчисления значений компонент вектора состояний
вектора состояния определяются выбором единиц измерения для соответствующего ресурса (характеристики). Очевидно, что в подавляющем большинстве случаев это денежные измерители в той или иной валюте, но, в принципе, возможны и иные формы учета. Например, через перечисление видов, количество и номиналы облигаций или же через указание числа мерных слитков, веса драгоценных камней и т. п. Для обобщения допустимых способов исчисления значений компонент вектора состояний 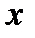 может быть введено понятие ресурсных единиц. Другими словами, состояние отдельного
может быть введено понятие ресурсных единиц. Другими словами, состояние отдельного 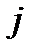 - го ресурса отождествляется с некоторым элементом множества неотрицательных действительных чисел
- го ресурса отождествляется с некоторым элементом множества неотрицательных действительных чисел  , геометрическим образом которого является положительная полуось вещественной прямой. Таким образом, состояние банка в целом может быть представлено некоторой точкой неотрицательного ортанта
, геометрическим образом которого является положительная полуось вещественной прямой. Таким образом, состояние банка в целом может быть представлено некоторой точкой неотрицательного ортанта  -мерного евклидова пространства:
-мерного евклидова пространства:

Множество всех возможных (допустимых) точек (векторов) 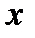 образует пространство состояний банка.
образует пространство состояний банка.
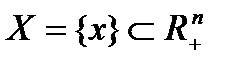 .
.
На основе элементов вектора 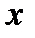 , представляющих собой первичные характеристики состояния банка, могут быть получены некоторые производные (вторичные) характеристики
, представляющих собой первичные характеристики состояния банка, могут быть получены некоторые производные (вторичные) характеристики
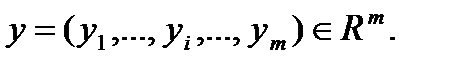
Очевидно, что вектор производных характеристик 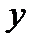 при таком задании представляет собой функцию от вектора исходных характеристик
при таком задании представляет собой функцию от вектора исходных характеристик

В качестве типичного примера вторичных характеристик состояния банка может быть приведена система обязательных финансовых нормативов (коэффициентов), устанавливаемых центральными банками или иными регулирующими органами.
Для того чтобы обеспечить в модели учет фактора времени, следует задать некоторое множество  , элементы которого
, элементы которого  будем называть моментами времени. Особо подчеркнем высокий уровень абстракции такого способа ввода понятия «время», относительно которого существует и развивается моделируемая система. Очевидно, что данное определение охватывает в качестве частных случаев как непрерывное, так и дискретное время. Традиционно в качестве модели непрерывного физического времени используется множество точек бесконечной одномерной действительной числовой оси
будем называть моментами времени. Особо подчеркнем высокий уровень абстракции такого способа ввода понятия «время», относительно которого существует и развивается моделируемая система. Очевидно, что данное определение охватывает в качестве частных случаев как непрерывное, так и дискретное время. Традиционно в качестве модели непрерывного физического времени используется множество точек бесконечной одномерной действительной числовой оси  с фиксированным началом отсчета, а множество всех учитываемых моментов времени
с фиксированным началом отсчета, а множество всех учитываемых моментов времени  в этом случае представляет собой некоторый отрезок на этой оси (замкнутый или открытый):
в этом случае представляет собой некоторый отрезок на этой оси (замкнутый или открытый):
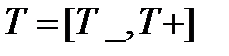 или
или 
При задании в модели банка непрерывного времени состояние  -й характеристики может рассматриваться как значение функции
-й характеристики может рассматриваться как значение функции  , определенной на множестве
, определенной на множестве  и принимающей значения из множества
и принимающей значения из множества  . Тогда график
. Тогда график  играет роль траектории изменения во времени
играет роль траектории изменения во времени  -й характеристики. Соответственно состояние банка в целом есть значение векторной функции от времени
-й характеристики. Соответственно состояние банка в целом есть значение векторной функции от времени
 (2.5.2)
(2.5.2)
а траектория системы  представляет собой некоторую кривую в
представляет собой некоторую кривую в
 -мерном пространстве. Каждая точка такой траектории является элементом пространства возможных состояний банка
-мерном пространстве. Каждая точка такой траектории является элементом пространства возможных состояний банка  .
.
На основе введенных выше понятий может быть определен принципиально новый термин – «поток». Поток (flow) – экономическая величина, которая измеряется в движении с учетом рассматриваемого временного интервала. Размерность потока – это объем, деленный на время. В то же время объем (stock, volume) – величина, характеризующая значение какого-либо показателя на некоторый фиксированный момент времени.
Содержательная сторона понятия «поток» связана с понятием скорости изменения состояния системы. Если предположить, что функции  , задающие траектории изменения характеристик состояния банка, являются «гладкими», т. е. дифференцируемыми во всех точках промежутка
, задающие траектории изменения характеристик состояния банка, являются «гладкими», т. е. дифференцируемыми во всех точках промежутка  , то соответствующие первые производные
, то соответствующие первые производные
 (2.5.3)
(2.5.3)
могут быть интерпретированы как скорости изменения этих характеристик. Учитывая, что  является не чем иным, как объемом
является не чем иным, как объемом  -го ресурса, выраженным в некоторых ресурсных единицах (р. е.), то функция
-го ресурса, выраженным в некоторых ресурсных единицах (р. е.), то функция  представляет собой ресурсный поток, определяющий в каждый момент времени
представляет собой ресурсный поток, определяющий в каждый момент времени  скорость изменения величины ресурса (
скорость изменения величины ресурса ( -й компоненты состояния банка) в ресурсных единицах, деленных на единицы измерения времени. Например, в рублях в день. При рассмотрении конкретного ресурса мы получаем конкретные виды потоков: финансовый поток, денежный поток, поток наличности и т. п.
-й компоненты состояния банка) в ресурсных единицах, деленных на единицы измерения времени. Например, в рублях в день. При рассмотрении конкретного ресурса мы получаем конкретные виды потоков: финансовый поток, денежный поток, поток наличности и т. п.
Динамика банка в целом может быть описана с помощью векторного ресурсного потока
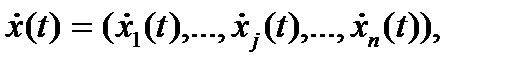
задающего вектор скоростей изменения состояний изучаемого объекта в пространстве  . При этом значение отдельной характеристики объекта
. При этом значение отдельной характеристики объекта
( -й компоненты вектора состояния) для любого момента времени
-й компоненты вектора состояния) для любого момента времени  определяется по формуле
определяется по формуле
 . (2.5.4)
. (2.5.4)
С введением понятия ресурсного потока мы получаем возможность сформулировать модель, базирующуюся на представлении банка как системы (вектора) первичных ресурсных потоков
 ,
,  (2.5.5)
(2.5.5)
Модель (2.5.5) является альтернативой модели (2.5.2), в основе которой лежит система (вектор) состояний. Основываясь на формулах (2.5.3) и (2.5.4), можно прийти к заключению, что оба способа формализованного представления банка при выполнении условий дифференцируемости функций  будут эквивалентными.
будут эквивалентными.
Следующий шаг в процессе совершенствования рассматриваемого класса моделей связан с учетом в них факторов риска и неопределенности.
Для описания неопределенности, присутствующей в траектории состояний, в которых может оказаться исследуемый объект, удобно воспользоваться терминологией теории случайных процессов. Под случайным процессом (случайной функцией времени, стохастический процесс или вероятностный процесс) понимается функция  которая может иметь ту или иную конкретную реализацию (траекторию) из некоторого фиксированного множества возможных траекторий
которая может иметь ту или иную конкретную реализацию (траекторию) из некоторого фиксированного множества возможных траекторий 
Обобщая сказанное, получаем, что в условиях неопределенности моделью динамики состояния банка может служить векторный случайный процесс

каждая компонента  которого описывает стохастическую динамику
которого описывает стохастическую динамику  -й характеристики (ресурса) банка. По аналогии фактор неопределенности, присутствующий в системе ресурсных потоков банка, может быть описан в формализованном виде при помощи векторного случайного процесса
-й характеристики (ресурса) банка. По аналогии фактор неопределенности, присутствующий в системе ресурсных потоков банка, может быть описан в формализованном виде при помощи векторного случайного процесса
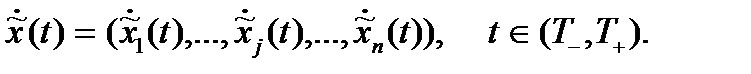
Одновременно заметим, что модели, основывающиеся на задании стохастических процессов в общем виде, имеют исключительно теоретическое значение и предназначены лишь для изложения на принципиальном уровне идей применения соответствующего математического аппарата. Исследования, направленные на содержательный анализ закономерностей работы банков, так или иначе должны опираться на предпосылки, конкретизирующие тип и параметры используемых в них случайных величин и функций.
Рассмотрение моделей управления привлеченными ресурсами в финансовой фирме логично начать с моделей, носящих описательный характер, т. е. отражающих тенденции в поведении величины того или иного ресурса безотносительно к сознательным управляющим воздействиям на нее. Очевидно, изменения таких величин являются результатом влияния различных по своей природе факторов, носящих как по силе, так и по природе своего проявления случайный характер, что и предопределяет использование для отражения процесса изменения объемов финансовых ресурсов банка теории оптимального управления и теории случайных процессов.
Рассмотрим простейшая мультипликативная стохастическая модель динамики финансового ресурса. Исследование моделей поведения объемов ресурсов финансовой фирмы начнем с наиболее простой стохастической модели для отдельно взятого ресурса. В качестве наблюдаемого ресурса могут выступать, как привлеченные средства в целом, так и депозиты до востребования, срочные депозиты и т. д.
В основе исследуемой модели лежит предпосылка о возможности отслеживать объемы изучаемого ресурса через дискретные равноотстоящие промежутки времени  . Обозначим через
. Обозначим через 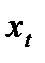 – объем в момент времени
– объем в момент времени  .
.
Предположим, что переход объема ресурса от момента времени  к моменту времени
к моменту времени  описывается соотношением
описывается соотношением
 , (2.5.6)
, (2.5.6)
где  – положительный коэффициент элементарного перехода от
– положительный коэффициент элементарного перехода от  к
к 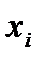

 . (2.5.7)
. (2.5.7)
Эта формула может быть интерпретирована как мультипликативная модель ресурса на дискретном отрезке времени 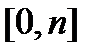 .
.
Если наблюдаемые значения  коэффициентов элементарных переходов интерпретировать как значения соответствующих случайных величин
коэффициентов элементарных переходов интерпретировать как значения соответствующих случайных величин  , то формула (2.5.7) дает следующую стохастическую мультипликативную модель динамики ресурса на дискретном отрезке времени
, то формула (2.5.7) дает следующую стохастическую мультипликативную модель динамики ресурса на дискретном отрезке времени  :
:
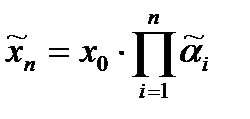 , (2.5.8)
, (2.5.8)
где  – случайное значение величины ресурса в момент времени
– случайное значение величины ресурса в момент времени
 .
.
Предположим, что все случайные коэффициенты элементарных переходов независимы, и каждый из этих коэффициентов имеет логарифмически нормальное распределение  . Иными словами, предполагается, что натуральный логарифм случайной величины
. Иными словами, предполагается, что натуральный логарифм случайной величины  имеет нормальное распределение с математическим ожиданием
имеет нормальное распределение с математическим ожиданием  и с дисперсией
и с дисперсией 

Знание плотности распределения
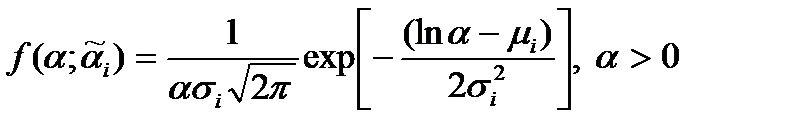 , (2.5.9)
, (2.5.9)
случайной величины  позволяет найти математическое ожидание
позволяет найти математическое ожидание
 , (2.5.10)
, (2.5.10)
второй начальный момент
 (2.5.11)
(2.5.11)
и дисперсию
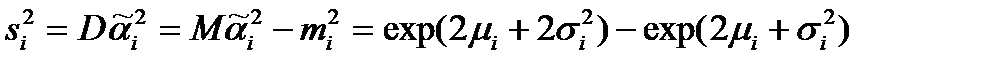 (2.5.12)
(2.5.12)
случайного коэффициента элементарного перехода.



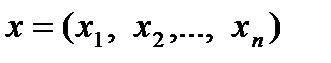 (2.5.1)
(2.5.1) определяется степенью детализации представления банка в модели. Это может быть, допустим, объем депозитов до востребования или же объем конкретного вклада, принадлежащего конкретному лицу.
определяется степенью детализации представления банка в модели. Это может быть, допустим, объем депозитов до востребования или же объем конкретного вклада, принадлежащего конкретному лицу.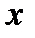 могут интерпретироваться как обычные статьи баланса, а их количество и структура соответствуют уровню его агрегированности (ежедневный, включающий счета второго порядка, или укрупненный квартальный).
могут интерпретироваться как обычные статьи баланса, а их количество и структура соответствуют уровню его агрегированности (ежедневный, включающий счета второго порядка, или укрупненный квартальный). вектора состояния определяются выбором единиц измерения для соответствующего ресурса (характеристики). Очевидно, что в подавляющем большинстве случаев это денежные измерители в той или иной валюте, но, в принципе, возможны и иные формы учета. Например, через перечисление видов, количество и номиналы облигаций или же через указание числа мерных слитков, веса драгоценных камней и т. п. Для обобщения допустимых способов исчисления значений компонент вектора состояний
вектора состояния определяются выбором единиц измерения для соответствующего ресурса (характеристики). Очевидно, что в подавляющем большинстве случаев это денежные измерители в той или иной валюте, но, в принципе, возможны и иные формы учета. Например, через перечисление видов, количество и номиналы облигаций или же через указание числа мерных слитков, веса драгоценных камней и т. п. Для обобщения допустимых способов исчисления значений компонент вектора состояний 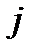 - го ресурса отождествляется с некоторым элементом множества неотрицательных действительных чисел
- го ресурса отождествляется с некоторым элементом множества неотрицательных действительных чисел  , геометрическим образом которого является положительная полуось вещественной прямой. Таким образом, состояние банка в целом может быть представлено некоторой точкой неотрицательного ортанта
, геометрическим образом которого является положительная полуось вещественной прямой. Таким образом, состояние банка в целом может быть представлено некоторой точкой неотрицательного ортанта  -мерного евклидова пространства:
-мерного евклидова пространства:
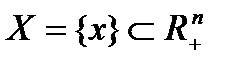 .
.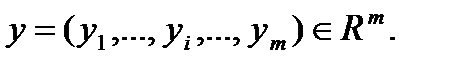
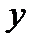 при таком задании представляет собой функцию от вектора исходных характеристик
при таком задании представляет собой функцию от вектора исходных характеристик
 , элементы которого
, элементы которого  будем называть моментами времени. Особо подчеркнем высокий уровень абстракции такого способа ввода понятия «время», относительно которого существует и развивается моделируемая система. Очевидно, что данное определение охватывает в качестве частных случаев как непрерывное, так и дискретное время. Традиционно в качестве модели непрерывного физического времени используется множество точек бесконечной одномерной действительной числовой оси
будем называть моментами времени. Особо подчеркнем высокий уровень абстракции такого способа ввода понятия «время», относительно которого существует и развивается моделируемая система. Очевидно, что данное определение охватывает в качестве частных случаев как непрерывное, так и дискретное время. Традиционно в качестве модели непрерывного физического времени используется множество точек бесконечной одномерной действительной числовой оси  с фиксированным началом отсчета, а множество всех учитываемых моментов времени
с фиксированным началом отсчета, а множество всех учитываемых моментов времени 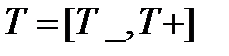 или
или 
 -й характеристики может рассматриваться как значение функции
-й характеристики может рассматриваться как значение функции  , определенной на множестве
, определенной на множестве  . Тогда график
. Тогда график  играет роль траектории изменения во времени
играет роль траектории изменения во времени  (2.5.2)
(2.5.2) представляет собой некоторую кривую в
представляет собой некоторую кривую в  -мерном пространстве. Каждая точка такой траектории является элементом пространства возможных состояний банка
-мерном пространстве. Каждая точка такой траектории является элементом пространства возможных состояний банка  .
. , то соответствующие первые производные
, то соответствующие первые производные (2.5.3)
(2.5.3) представляет собой ресурсный поток, определяющий в каждый момент времени
представляет собой ресурсный поток, определяющий в каждый момент времени  скорость изменения величины ресурса (
скорость изменения величины ресурса (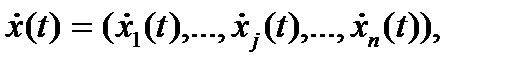
 . При этом значение отдельной характеристики объекта
. При этом значение отдельной характеристики объекта  определяется по формуле
определяется по формуле . (2.5.4)
. (2.5.4) которая может иметь ту или иную конкретную реализацию (траекторию) из некоторого фиксированного множества возможных траекторий
которая может иметь ту или иную конкретную реализацию (траекторию) из некоторого фиксированного множества возможных траекторий 

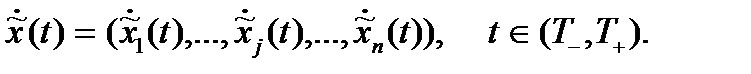
 . Обозначим через
. Обозначим через 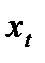 – объем в момент времени
– объем в момент времени  .
. к моменту времени
к моменту времени  описывается соотношением
описывается соотношением , (2.5.6)
, (2.5.6) – положительный коэффициент элементарного перехода от
– положительный коэффициент элементарного перехода от  к
к 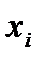

 . (2.5.7)
. (2.5.7)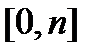 .
. коэффициентов элементарных переходов интерпретировать как значения соответствующих случайных величин
коэффициентов элементарных переходов интерпретировать как значения соответствующих случайных величин  , то формула (2.5.7) дает следующую стохастическую мультипликативную модель динамики ресурса на дискретном отрезке времени
, то формула (2.5.7) дает следующую стохастическую мультипликативную модель динамики ресурса на дискретном отрезке времени  :
: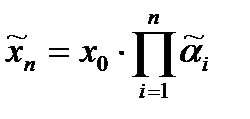 , (2.5.8)
, (2.5.8) – случайное значение величины ресурса в момент времени
– случайное значение величины ресурса в момент времени  .
. . Иными словами, предполагается, что натуральный логарифм случайной величины
. Иными словами, предполагается, что натуральный логарифм случайной величины  имеет нормальное распределение с математическим ожиданием
имеет нормальное распределение с математическим ожиданием  и с дисперсией
и с дисперсией 

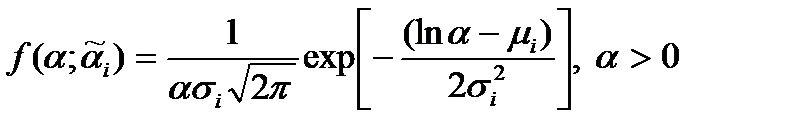 , (2.5.9)
, (2.5.9) , (2.5.10)
, (2.5.10) (2.5.11)
(2.5.11)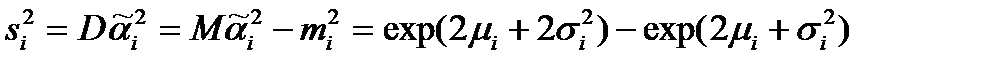 (2.5.12)
(2.5.12)
