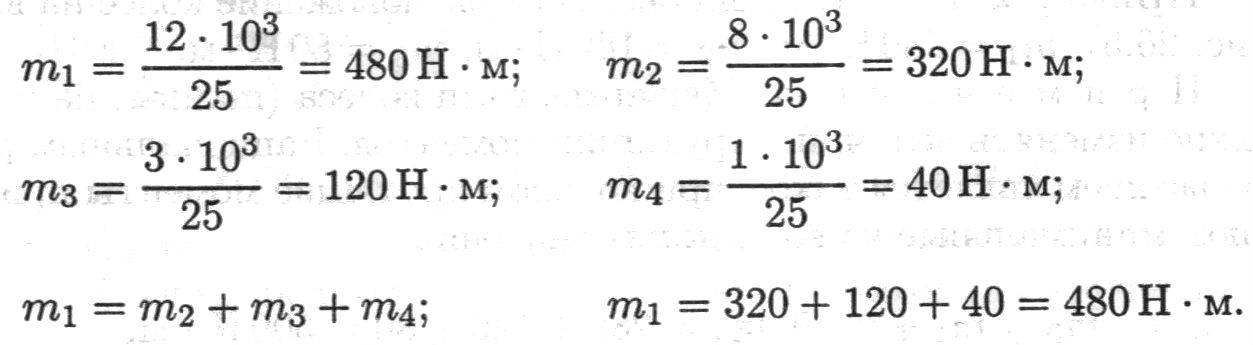МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ВЫПОЛНЕНИЮ РАСЧЕТНОЙ ЧАСТИ КОНТРОЛЬНЫХ ВНЕАУДИТОРНЫХ ЗАДАНИЙ
ПО ДИСЦИПЛИНЕ «ТЕХНИЧЕСКАЯ МЕХАНИКА»
для студентов заочной формы обучения
по специальности:
08.02.09 «Монтаж наладка и эксплуатация электрооборудования
промышленных и гражданских зданий»
г. Красноярск 2016
Методическое пособие составлено в соответствии с требованиями федерального государственного образовательного стандарта утвержденного приказом Министерства образования и науки Российской Федерации №282 от «06» апреля 2010г. к результатам освоения основной профессиональной образовательной программы и предназначены для консультативной помощи студентам заочной формы обучения при выполнении расчетной части внеаудиторных контрольных заданий.
| РЕКОМЕНДОВАНО
Методическим советом Красноярского политехнического техникума
Зам директора по УР
_________________ Л.В. Афанасьева
Протокол №____ от «___» ____ 2016г.
| УТВЕРЖДЕНО
Цикловой комиссией (спец. дисциплин электромеханического цикла)
Председатель ПЦК
_________________В.В.Бузаев
Протокол №_____ от «____» ______ 2016г.
|
| | |
Организация-разработчик:
КГБПОУ «Красноярский политехнический техникум»
Разработчик(и):
Г.М. Сазонова, преподаватель спец. дисциплин механического цикла КГБПОУ «Красноярский политехнический техникум»
Рецензент:
В.В.Бузаев председатель цикловой комиссии (спец. дисциплин электромеханического цикла)), преподаватель высшей категории КГБПОУ «Красноярский политехнический техникум»
В пособии представлены рекомендации по выполнению и оформлению расчетной части внеаудиторных контрольных заданий и внеаудиторные задания по дисциплине «Техническая механика» с методическими указаниями к решению задач, приведены примеры решения
Содержание
1. Введение. 4
2. Перечень (ОК) и (ПК), формируемых при изучении
дисциплины 4
3. Общие методические указания 5
4. Наименование разделов и тем в соответствии с рабочей
программой изучаемой дисциплиной 6
5. Рекомендации к изучению разделов и тем, а также по
решению задач 8
6. Краткие методические указания по выполнению
контрольной работы. Раздел I.Теоретическая механика. 10
7. К задаче №1 10
8. К задаче №2 12
9. К задаче №3 14
10. Раздел II.Сопротивление материалов. 19
11. К задаче №4 20
12. К задаче №5 23
13. К задаче №6 27
14. К задаче №7 32
Задания для контрольной работы: 35
15. Задача №1 35
16. Задача №2 36
17. Задача №3 38
18. Задача №4 39
19. Задача №5 41
20. Задача №6 41
21. Задача №7 46
22. Задача №8 43
22. Вопросы для подготовки к экзаменам 47
23. Критерии оценок письменных работ студентов 49
24. Список использованной литературы 50
Введение
Предмет «Техническая механика» для механических специальностей техникума состоит из трех частей: теоретической механики, сопротивления материалов и деталей машин.
Учебная программа дисциплины «Техническая механика» предусматривает изучение общих законов равновесия и движения материальных тел; основных методов расчета на прочность, жесткость и устойчивость отдельных деталей узлов машин; изучение устройства, области применения и основ проектирования деталей машин и узлов общего назначения.
Перечень общих компетенций (ОК), Формируемых при изучении дисциплин
ОК1.Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
ОК2.Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
Перечень профессиональных компетенций (ПК), осваиваемых студентом при изучении дисциплины:
Организация и выполнение работ по эксплуатации и ремонту электроустановок.
ПК1.3.Организовывать и производить ремонт электроустановок промышленных и гражданских зданий.
Организация и выполнение работ по монтажу и наладке электрооборудования промышленных и гражданских зданий.
ПК2.1.Организовывать и производить монтаж силового электрооборудования промышленных и гражданских зданий с соблюдением технологической последовательности.
ПК2.2.Организовывать и производить монтаж осветительного электрооборудования промышленных и гражданских зданий с соблюдением технологической последовательности.
ПК2.3.Организовывать и производить наладку и испытания устройств электрооборудования промышленных и граждан
ПК2.4.Участвовать в проектировании силового и осветительного электрооборудования.
Общие методические указания
Настоящие методические указания содержат: программу предмета, перечень учебной литературы, три задания по изучению предмета (по теоретической механике, сопротивлению материалов, деталей машин.
Настоящее пособие составлено в соответствии с программой по предмету «Техническая механика» для машиностроительных специальностей техникумов. Оно предназначено для оказания помощи студентам в самостоятельном изучении предмета и выполнения контрольной работы
Вариант контрольной работы определяется по последней цифре шифра студента.
После изучения материала каждого задания выполняется контрольная работа. Задачи контрольной работы даны в последовательности тем программы, поэтому они должны решаться в том же порядке.
После тщательного изучения материала, конспектируя основные определения, доказательства, правила, необходимо ответить на вопросы для самопроверки.
Закрепление усвоения материала производится путем разбора решенных задач, в приведенных учебниках и настоящем пособии.
В случае затруднений в понимании какого либо вопроса необходимо обратиться за разъяснением в техникум.
При выполнении контрольной работы необходимо соблюдать следующие требования:
а) контрольная работа выполняется в отдельной тетради или в компьютерном варианте с титульным листом в файле.
б) на обложке тетради или титульном листе пишется фамилия, имя, отчество, номер личного дела (шифр), наименование предмета, дата отправления, почтовый адрес студента.
в) на последней странице, указывается наименование и год издания методического пособия, из которого взято задание
г) тексты условий задач переписываются обязательно.
д) к задачам должны быть даны необходимые чертежи, схемы пояснения к решениям задач, вычисления выполнить с точностью до соты
Выполненную контрольную работу следует своевременно выслать в техникум. после получения зачтенной работы студенту следует внимательно изучить рецензию и все замечания и ошибки. Не зачтенная работа переделывается частично по указанию преподавателя или выполняется по другому варианту.
Программой предусмотрено выполнение студентами практических работ. По разделам «техническая механика», «сопротивление материалов», «детали машин» в соответствии с календарно-тематическими планами
Наименование разделов и тем в соответствии с рабочей программой изучаемой дисциплиной
| | |
| Раздел 1. Теоретическая механика 81.ч
| | |
|
| Наименование тем
| Практические работы
| Домашняя контрольная работа
|
| Олофинская В.П.[л1],с4-12],АркушаА.И.[л2],с4-12
|
| |
| Тема1.1.Основные положения и аксиомы статики.
| | | |
|
| Сила. Аксиомы статики
|
|
| | | |
| Тема1.2 Плоская система сходящихся сил.
| |
| |
|
| Силовой многоугольник. Проекция силы на ось.
|
| +
|
| Л.1,с19-16,Л.2,с16-25, работа с учебником
|
| |
|
| Условия равновесия системы.
|
|
| |
| Тема 1.3 Пара сил и момент силы относительно точки.
| | |
| |
|
| Пара сил. Момент пары сил.
|
|
|
| Л.1,с28-34,Л.2,с27-34.Работа с учебником
|
| |
|
| Практическая работа № 1 «Определение равнодействующей плоской системы сходящихся сил»
|
+
|
| |
| Тема1.4 Плоская система произвольно расположенных сил.
| |
| |
|
| Опоры балочных систем. Решение задач.
|
|
|
| Л.1,с42-50,контр. вопросы.
|
| |
|
| Самостоятельная работа
|
|
| |
|
| Практическая работа №2
«Определение опорных реакций балок»
| +
| +
| Отчет о работе
|
| |
|
| Центр тяжести простых геометрических фигур Центр тяжести стандартных профилей.
| | | | Л.1,с68,контр. вопросы
| | |
|
| Практическая работа № 3 «Определение центра тяжести составного сечения»
|
|
| Л.1,с67-77,контр.вопросы.
| | |
|
| ОКР №1
|
|
| Л.1,с70-77,примеры задач.
| | |
|
| Практическая работа № 4 «Определение центра тяжести плоских фигур».
| +
| +
| |
| Тема 1.6 Кинематика. Основные понятия кинематики
| |
|
| январь
|
|
| Прямолинейное и вращательное движение тела.
|
|
|
| Отчет о работе
|
| |
| Тема 1.7 Кинематика точки
| |
|
| январь
|
|
| Способы задания движения точки.
Простейшее движение твердого тела.
Скорость точки, ускорение.
|
|
|
| Л.1,с98-108,Л.2,с98-106,работа с учебником
|
| |
| Тема1.8 Динамика. Основные положения и аксиомы динамики
| |
|
| Основные понятия и аксиомы динамики. Метод кинетостатики.
Принцип Даламбера.
|
|
| |
| Тема 1 9 Работа и мощность.
| |
|
| Работа при поступательном движении.
КПД.
|
|
| |
| Раздел.2 Сопротивление материалов. 72.ч
| |
| Тема 2.1 Основные положения.
| |
|
| Метод сечений. Напряжения..
|
|
| |
| Тема 2.2 Растяжение и сжатие
|
| |
|
| Внутренние силовые факторы. при растяжении и сжатии. Эпюры.
|
|
| |
|
| Закон Гука. Продольная и поперечная деформации.
|
|
| |
|
| Механические испытания и свойства
материалов
|
|
|
| |
|
| .Практическая работа № 5 «Испытание
Материалов на растяжение»
|
|
|
| |
|
| Практическая работа№ 6 «Построение эпюр продольных сил и нормальных напряжений, абсолютное удлинение»
|
+
|
|
+
| |
|
| Практическая работа № 7 «Расчеты на прочность и жесткость при растяжении и сжатии».
|
|
| |
| Тема 2.3 Расчеты на срез и смятие.
| |
|
| Срез и смятие (расчеты).
|
|
| |
|
| Условия прочности. Решение задач.
|
|
| |
|
| Практическая работа № 8 «Испытание
Металлических образцов на срез»
|
|
| |
| Тема 2.5 Кручение.
| |
|
| Сдвиг. Кручение. Напряжения при кручении. Расчеты на прочность при кручении..
|
|
+
| |
| Тема 2.6 Изгиб
| |
|
| Расчеты на прочность при изгибе
|
|
| |
|
| Практическая работа № 9 «Построение эпюр поперечных сил и изгибающих моментов»
|
|
+
| |
|
| Зависимость между интенсивностью поперечной силы и изгибающим моментом.Касательные напряжения при изгибе.
|
|
| |
| Тема 2.7 Устойчивость сжатых стержней
| |
|
| Устойчивость сжатых стержней.
Критическая сила..
|
|
| |
|
| Формула Эйлера. Формула Ясинского.
|
|
| |
|
| Практическая работа № 10 «Определение устойчивости сжатых стержней»
|
|
| |
| Раздел 3. Детали машин
| |
|
| Классификация передач. Основные характеристики.
|
| +
| |
|
| Валы, оси, муфты, подшипники..
Назначение, классификация.
|
|
| |
|
| Практическая работа № 11
«Составление кинематических
схем механизмов»
| | +
| |
|
| Практическая работа № 12 «Изучение
конструкции конического редуктора»
|
| | |
|
| Практическая работа № 13
«Изучение конструкции
цилиндрического редуктора»
|
|
| |
|
| Практическая работа № 14 «Изучение
конструкции червячного редуктора»
|
|
| |
| Итого за семестр 54ч. / 27
| |
| Итого за год 86ч. / 43
| |
| | | | | | | | | | | | | | | | | |
Примечание: в таблице - «+» - обозначает на стадии выполнения
Рекомендации по изучению разделов и тем, а также решению задач
К задаче № 1.
К выполнению первой задачи следует приступить только после проработки и усвоения темы 1.1. «Основные понятия и аксиомы статики^ и темы 1.2. «Плоская система сходящихся сил». Порядок решения задач следующий:
1. Выявляется, какое тело (или точка) находится в состоянии равновесия.
2. Устанавливаются все действующие на тело силы (нагрузки) и изображаются на схеме в виде векторов,
3. Освобождается тело от связей, которые заменяются реакциями, изображающимися на схеме также векторами.
4. 4. При аналитическом решении задачи наносятся оси координат X и У, на которые проектируются активные и реактивные силы. При этом для упрощения решения одну из осей координат следует совместить с линией действия одной из неизвестных сил, чтобы получить одно уравнение с одним неизвестным
5. Составляются и решаются уравнения равновесия сходящихся сил.
Пример № 1
На шарнир В стержневой конструкции ABC (Рисунок 1,а)) действует сила F = 5 Кн. Требуется определить усилия в стержнях АВ и СВ.
Решение: Рассмотрим равновесие узла В, к которому приложена сила F.
Освободим этот узел от связей, мысленно вырезав его и заменив связи реакциями N1 и N2. (Рисунок 1,б)). Направление реакций связей примем от

Рисунок 1, а)- Схема стержневой конструкции АВС
узла, т.е. будем предполагать, что усилия в стержнях растягивающие.
Однако в результате решения может оказаться, что в стержнях, или в одном (Рисунок 1,а)) усилия получились со знаком минус, тогда это будет означать, что усилия будут сжимающими. ^Таким образом, на узел В действуют сходящиеся силы F и неизвестные нам реакции связей N1 и N2.
Примем точку В за начало координат и нанесем координатные оси X и У, причем одну из координатных осей (ось У) направим по линии действия неизвестной силы N1. Проектируя все силы, действующие на узел В, на координатные оси, (Рисунки 1, б); 1, в)), получим:
. 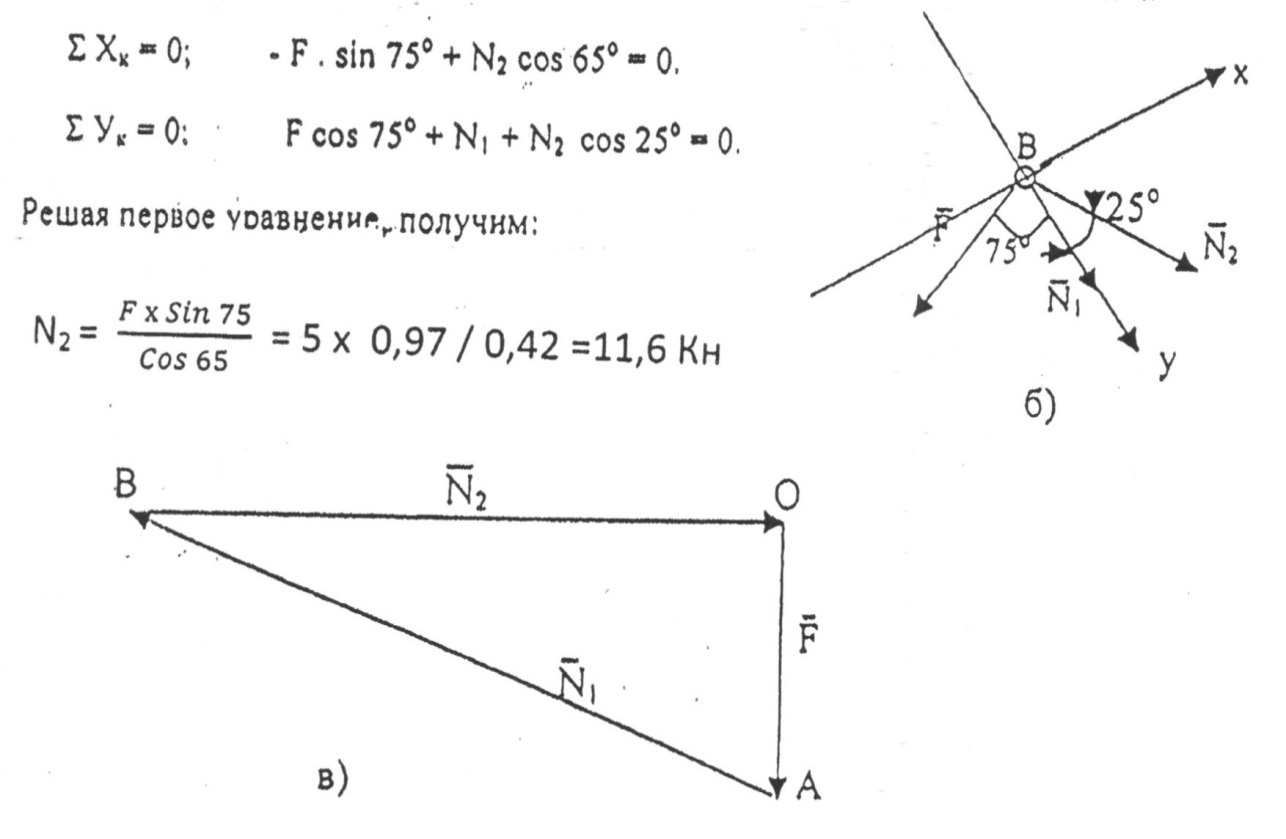 Рисунок 1, б)-Аналитический метод решения задачи, Рисунок 1, в)- Графический метод решения задачи
Рисунок 1, б)-Аналитический метод решения задачи, Рисунок 1, в)- Графический метод решения задачи
Величина усилия N2 получена со знаком плюс, следовательно стержень ВС растянут. Из решения второго уравнения получаем: N1 = -Fхcos 75°-N2 х cos 25°=-5х 0,26-11,55х0,91 =-11,8 кН. Величина усилия N1, получена со знаком минус, следовательно стержень АВ не растянут, а сжат.
Графический метод решения
Выбрав масштаб сил μF = 2 кН/см строим замкнутый силовой многоугольник (Рисунок 1,в)). Для этого на плоскости из произвольной точки О откладываем в принятом масштабе силу F. Ее можно отложить вертикально или параллельно силе F.
Из концов вектора ОА проводим линии, параллельно стержням АВ и ВС или проводим линию АВ под углом 750 к АО, а линию ОВ – под углом 1000 к вектору ОА до пересечения в точке О. Таким образом, получим замкнутый треугольник ОАВ, который выражает собой геометрическое условие равновесия сил, приложенных к углу В.
Линия АВ изображает собой величину, а стрелка указывает направление усилия N1 в стержне АВ. Измерив линию АВ и умножив на масштаб сил. находим величину усилия N1, равную 11 кН. Усилие N1 направлено к узлу В, значит стержень АВ сжат. Линию ВО в силовом многоугольнике выражает усилие N2 в выбранном масштабе, равное 11,6 кН. Значения усилий в стержнях N1 и 'N2 совпадают с результатами аналитического решения задачи. Направление усилия N2 от узла В означает, что стержень ВС растянут.
К задаче № 2.
Тема: Определение опорных реакции балок
Теоретическое обоснование:
Виды нагрузок
По способу приложения нагрузки делятся на сосредоточенные и распределенные. Если реально передача нагрузки происходит на пренебрежимо малой площадке (в точке), нагрузку называют сосредоточенной.
Часто нагрузка распределена по значительной площадке или линии (давление воды на плотину, давление снега на крышу и т.п.), тогда нагрузку считают распределенной. В задачах статики для абсолютно твердых тел распределенную нагрузку, можно заменить равнодействующей сосредоточенной силой.
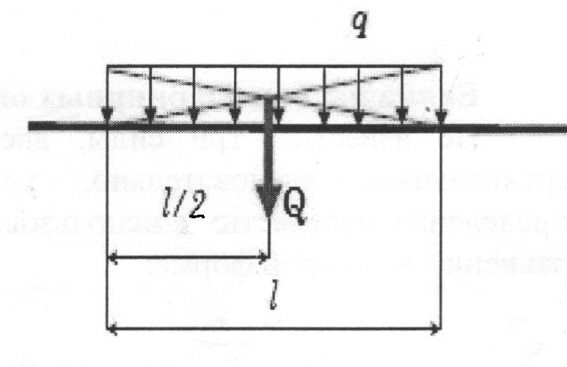 q – интенсивность нагрузки, Н/м.
q – интенсивность нагрузки, Н/м.
l–линия действия распределенной нагрузки, м.
Q=q х l равнодействующая распределенной нагрузки, Н.
Пример № 2
Для двухопорной балки (Рисунок 2) определить реакции опор RA и RB.
Решение:


Рисунок 2-Схема нагружения балки
Для проверки составляем сумму проекций всех сил на вертикальную осьY:
ΣFY=0., RA – F1 + F2 – RB = 0, 4,5 – 20 + 30 – 14,5 = 34,5 – 34,5 = 0.
Реакции найдены верно
К задаче № 3
Тема: Центр тяжести
Определение центра тяжести плоских фигур.
Цель: научиться определять положение центра тяжести сложных геометрических фигур.
Теоретическое обоснование:
Сила тяжести — равнодействующая сил притяжения к Земле, она распределена по всему объему тела. Силы притяжения, приложенные к частицам твердого тела, образуют систему сил, линии, действия которых сходятся в центре Земли. Поскольку радиус Земли значительно больше размеров любого земного тела, силы притяжения можно считать параллельными.
Для определения точки приложения силы тяжести (равнодействующей параллельных сил) используем теорему Вариньона о моменте равнодействующей: Момент равнодействующей относительно оси равен алгебраической сумме моментов сил системы относительно этой оси.
Изображаем тело, составленное из некоторых частей, в пространственной системе координат.
Тело состоит из частей, силы, тяжести которых приложены в центрах тяжести (ЦТ) этих частей.
Пусть равнодействующая (сила тяжести всего тела) приложена в неизвестном пока центре С.
хс, ус и zс — координаты центра тяжести С.
хк, ук и zк — координаты центров тяжести частей тела.
Из теоремы Вариота следует: 
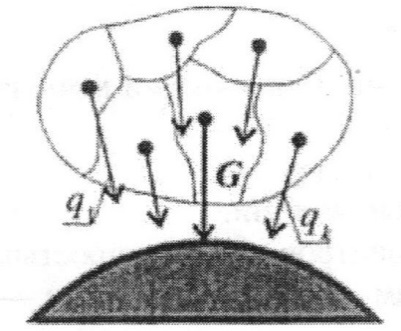

К задаче № 4
К решению четвертой задачи контрольной работы следует приступать после изучения темы «Растяжение и сжатие», метода сечений и разбора решенных примеров в данном пособии.
Задача требует от учащегося умения определить продольные силы, нормальные напряжения, удлинения и построить эпюры N и σ.
Растяжением (сжатием) называют такое нагружение бруса, при котором в поперечных сечениях возникает только один внутренний силовой фактор — продольная сила N, в любом поперечном сечении бруса численно равная алгебраической сумме внешних сил, действующих на оставленную часть бруса.
Простейшие случаи растяжения и сжатия представлены на (Рисунках 5, а); б); в); г)) в центрах тяжести торцевых поперечных сечений бруса приложены две равные противоположно направленные силы, линии действия которых совпадают с осью бруса.
Продольные силы N, соответствующие деформации растяжения, считаются положительными (Рисунок 5, а); в)), в противном случае они отрицательные (Рисунок 5, б); г)).
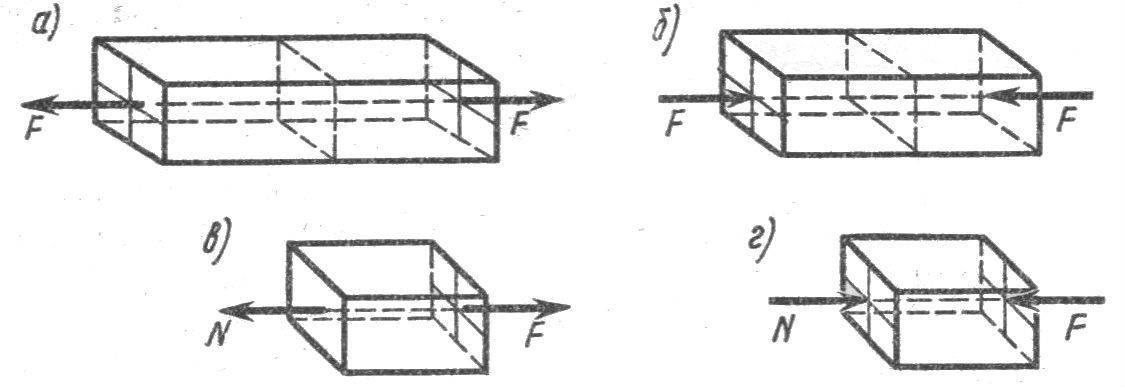
Рисунок 5, а);б);в);г)-Рисунки, поясняющие растяжение и сжатие
Удлинение (укорочение) бруса или отдельных его участков определяется по формуле Гука: ∆l = Nl / AE, (1)
которую можно представить еще в виде ∆l = σ (l / E), (2)
помня, что N / A = σ. (3)
Пример № 4
Для двухступенчатого бруса (Рисунок 6,а)) определить и построить эпюры продольных сил и нормальных напряжений. Определить удлинение (укорочение) бруса. Модуль упругости Е = 2 х 105 Н/мм2.

Рисунок 6-Рисунок,поясняющий растяжение и сжатие на участках бруса
Решение:
Разделим брус на участки, границы которых определяются сечениями, где изменяется площадь поперечного сечения или приложены внешние нагрузки. При составлении уравнений равновесия надо использовать правила знаков проекций сил, принятых в теоретической механике, а именно: проекция силы берется со знаком плюс, если ее направление совпадает с положительным направлением оси. Мысленно рассечем брус в пределах первого участка и отбросим верхнюю часть бруса (Рисунок 6,б)). Вместо отброшенной верхней части приложим внутреннюю силу N1, которая уравновешивается силой F1: N1 = F1 = 40 х 103Н = 40 кН.
Аналогично, в пределах участка II (Рисунок 6, в)) отбросим верхнюю часть бруса и рассмотрим оставленную часть бруса с действующей силой F1, которая уравновешивается продольной силой NI:.
NII = F1 = 40 х 103 H = 40 кН.
Продольная сила на участке III (Рисунок 6,г)) уравновешивается в сечении внешними силами F1 и F2 и равна их алгебраической сумме:
NIII = F1— F2 = 40 х 103 — 50 х 103 = — 10 х 103 = — 10 кН.
В пределах каждого участка нагружения продольная сила постоянна, а потому на эпюре изобразится линией, параллельной оси бруса. Эпюра
штрихуется линиями, перпендикулярными оси бруса.
Построим эпюру N (Рисунок 6,d)). Для этого параллельно оси бруса проведем базовую (нулевую) линию. Левее ее откладываем значение продольной силы, вызванной сжатием участка, а правее — растяжением. В пределах участка III брус сжат (Nш =—10 кН), в пределах участков II и I брус растянут (NII = NI = 40 кН).
Для определения напряжений σ в поперечных сечениях значение продольных сил необходимо разделить на площади соответствующих сечений: σ = N / A Площадь поперечного сечения бруса первого участка:
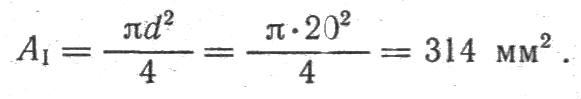
Площадь поперечного сечения бруса на участках II и III
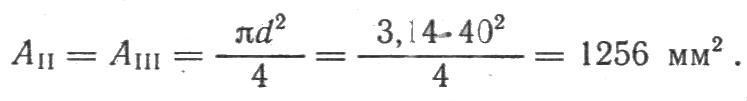
Находим напряжения на отдельных участках бруса по формуле (3) и строим эпюру (Рисунок 6,е)):

В соответствии с полученными значениями напряжений строим эпюру нормальных напряжений.
При построении эпюр продольных сил и нормальных напряжений нет необходимости изображать отдельно отсеченные части бруса, достаточно обратить внимание на то, что продольная сила, возникающая в произвольном сечении, равна алгебраической сумме всех внешних сил, приложенных к брусу по одну сторону от рассматриваемого сечения, а нормальное напряжение равно отношению продольной силы к соответствующей площади поперечного сечения. Кроме того, при построении эпюр и проверке их правильности следует руководствоваться следующими правилами:
1.Скачки на эпюрах N имеют место в точках приложения сосредоточенных сил. Величина скачка равна внешней силе.
2.На эпюре σ скачки имеют место не только в точках приложения сосредоточенных сил, но и в местах изменения площади поперечного сечения.
3.Знаки на участках эпюры σ должны совпадать со знаками на соответствующих участках эпюры N.
Полное удлинение бруса можно найти, воспользовавшись эпюрой N, представленной на (рисунок 6,д)), т. е. полное удлинение бруса равно алгебраической сумме удлинений его участков формулы (1),(2):
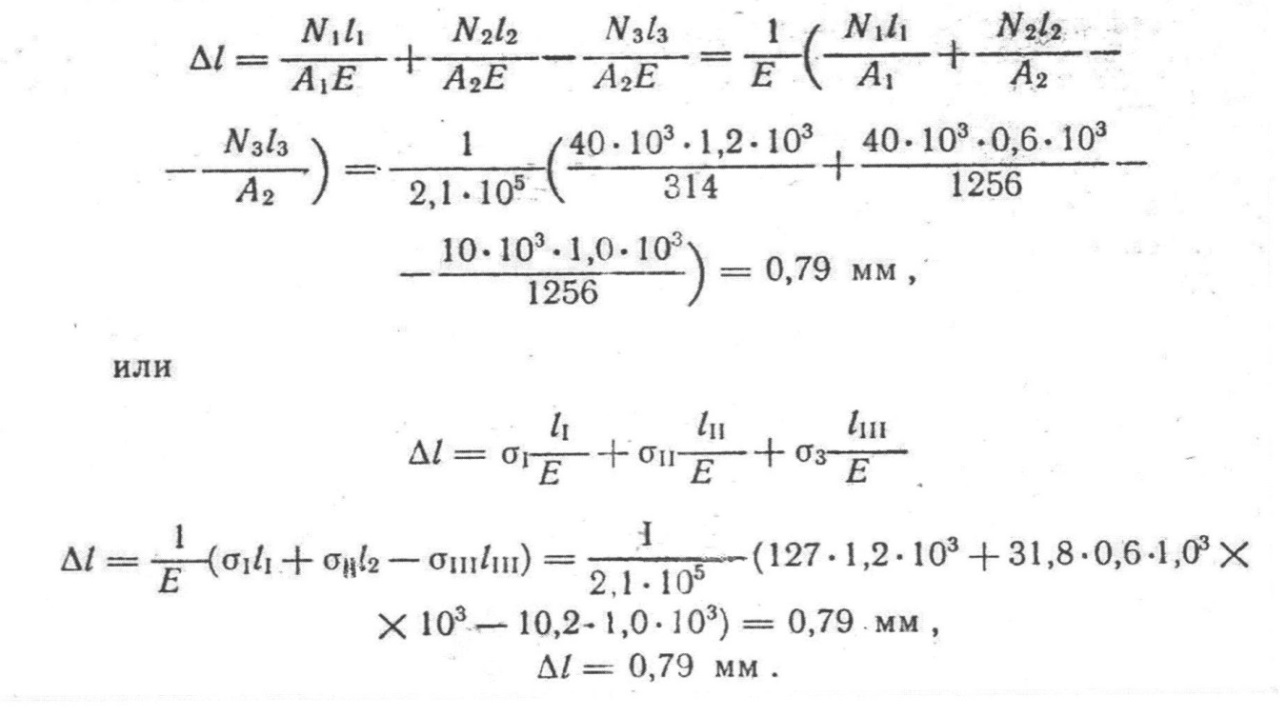
К задаче №5
Пятую задачу контрольной работы следует решать после изучения темы «Изгиб».
При прямом поперечном изгибе в поперечных сечениях балки возникает два внутренних силовых фактора — поперечная сила Qy и изгибающий момент Мх. Поперечная сила, возникающая в произвольном поперечном сечении, численно равна алгебраической сумме всех внешних сил (если все силы параллельны оси у), действующих на балку по одну сторону от рассматриваемого сечения.
Изгибающий момент в произвольном поперечном сечении численно равен алгебраической сумме моментов всех внешних сил, действующих на балку по одну сторону, от рассматриваемого сечения относительно той точки продольной оси балки, через которую проходит рассматриваемое сечение.
Для отыскания опасного сечения строят эпюры Qy и Мх, используя, метод сечения.
Условимся о правиле знаков: внешняя сила F, стремящаяся сдвинуть левую часть балки вверх относительно правой или (что то же самое) правую часть вниз относительно левой, вызовет возникновение положительной поперечной силы (Рисунок 7, а)). Внешняя сила или момент изгибающие балку таким образом, что сжатые волокна находятся сверху балки (Рисунок 7, б)), вызывают положительный изгибающий момент, который на эпюре Мх откладывается вверх от оси абсцисс, т. е. в сторону сжатых волокон, иначе можно сказать, что эпюры изгибающих моментов строятся на сжатом волокне.
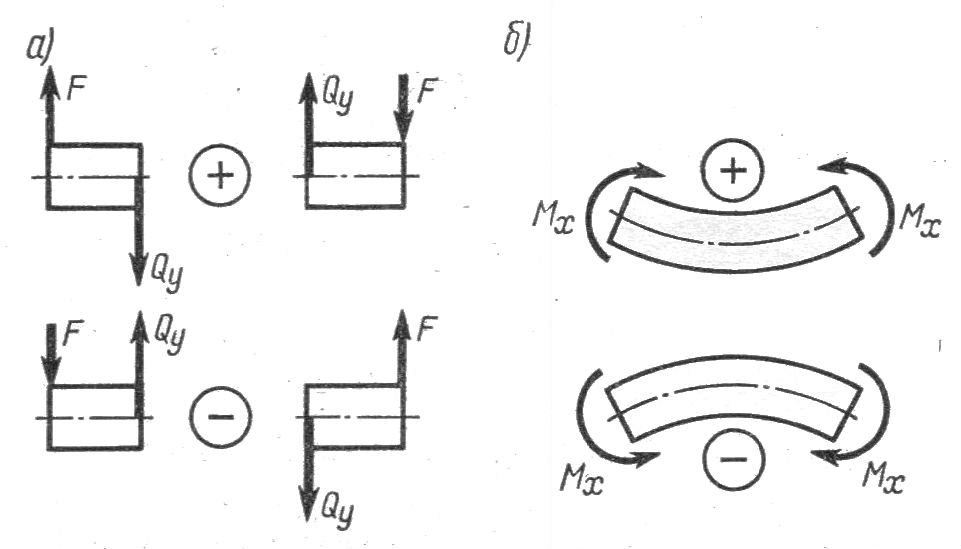
Рисунок 7-Правила определения знаков для изгибающих моментов и поперечных сил при изгибе
Для балок, имеющих много участков нагружения, т. е. нагруженных комбинацией нагрузок, целесообразно строить эпюры по характерным сечениям, а именно: вычислять поперечные силы и изгибающие моменты только для сечений, в которых эпюры претерпевают изменения, а затем, зная закон изменения эпюры между найденными сечениями, соединить их соответствующими линиями. К характерным относятся сечения, в которых приложены сосредоточенные силы или моменты, а также сечения, где начинается или кончается распределенная нагрузка.
Для того чтобы вычислить поперечную силу и изгибающий момент в произвольном сечении, необходимо мысленно рассечь плоскостью в этом месте балку и часть балки (любую), лежащую по одну сторону от рассматриваемого сечения, отбросить. Затем по действующим на оставленную часть балки внешним силам надо найти искомые значения Qy и Мх, причем знак их. надо определить по тому действию, какое оказывают внешние силы _на оставленную часть балки в соответствии с принятым ранее правилом знаков. При построении эпюры слева направо отбрасывается правая часть балки, a Qy и Мх находятся по силам, действующим на левую часть. При построении эпюры справа налево, наоборот, отбрасывается левая часть, a Qy и Мх определяются по силам, действующим на правую часть балки.
Для построения эпюр необходимо запомнить следующие правила.
1. На участке балки, где отсутствует распределенная нагрузка, эпюра Qy — прямая, параллельная базовой линии, а эпюра Мх наклонная прямая.
2. Под сосредоточенной силой на эпюре Qy наблюдается скачок, численно равный приложенной внешней силе, а на эпюре Мх — излом.
3. В точке приложения сосредоточенной пары сил на эпюре момента происходит скачок на размер момента этой пары, а эпюра Qy не претерпевает изменения.
4. На участке действия равномерно распределенной нагрузки эпюра Qy выражается наклонной прямой, а эпюра Mz — параболой, обращенной выпуклостью навстречу действию распределенной нагрузки.
5. Если на участке действия распределенной нагрузки эпюра пересекает базовую линию, то в этом сечении изгибающий момент принимает экстремальное значение.
6. Если на границе действия распределенной нагрузки не приложено сосредоточенных сил, то на эпюре Qy участок, параллельный оси абсцисс, переходит в наклонный без скачка, а параболическая и наклонная части эпюры Мх сопрягаются плавно без изгиба.
7. Изгибающий момент в концевых сечениях балки всегда равен нулю, за исключением случая, когда в концевом сечении действует сосредоточенная пара сил. В этом случае изгибающий момент в концевом сечении балки равен моменту действующей пары сил.
8. В сечении соответствующем заделке, QY и MX численно равны опорной реакции и реактивному моменту.
Решать задачу рекомендуется в такой последовательности
1) определить реакции опор балки (по двум уравнениям моментов:
одно – относительно левой опоры, второе – относительно правой),затем обязательно проверить правильность решения по уравнению проекций на ось, перпендикулярную балке;
2) построить эпюру поперечных сил;
3) построить эпюру изгибающих моментов (для этого целесообразно использовать метод построения по характерны сечениям, который достаточно подробно изложен в рекомендованных учебниках
4) по эпюре изгибающих моментов определить расчетный (наибольший по абсолютному значению) изгибающий момент, выразив его в Нмм;
5) для заданной стальной балки, например, квадратного сечения, подбираем размер «а», из условия прочности, формула (4) по нормальным напряжениям при изгибе, если [σ] = 160Мпа:
[σ] = [M]max / WX; (4)
WX = [M]max / [σ], где WX = а3 / 6 для квадрата, и отсюда найдем «а» -
сторону квадрата.
Пример № 5
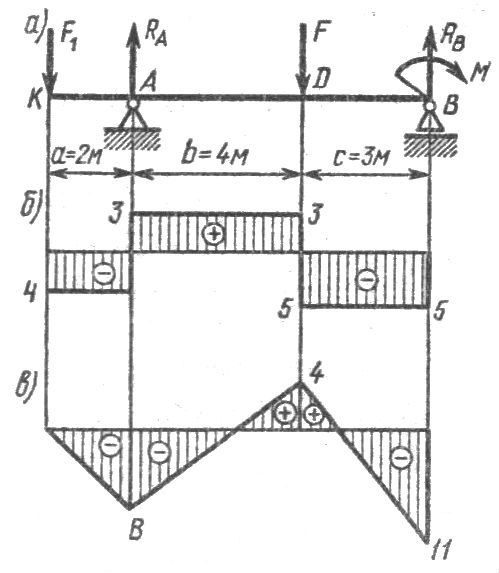
Рисунок 8-Схема нагружения балки, рассчитываемой на изгиб
Для балки (Рисунок 8,а)).построить эпюры поперечных сил и изгибающих моментов, если сосредоточенные силы F1= 4 кН; и F= 8кН, момент М = 11кН хм, расстояние а = 2м, в = 4м, с = 3м. Подобрать размер квадратного сечения заданной балки, принять для материала балки (сталь Ст.3) [  = 160 Мпа.
= 160 Мпа.
Решение: Определим опорные реакции:
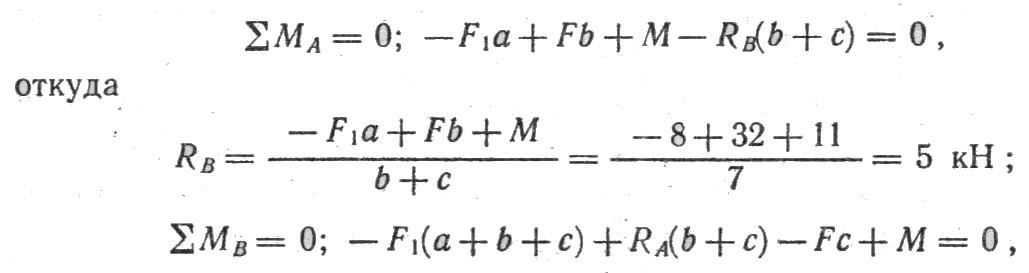
 Строим эпюру поперечных сил (Рисунок 8,б))
Строим эпюру поперечных сил (Рисунок 8,б))

Строим эпюру изгибающих моментов по характерным точкам К, А, D, В (Рисунок 8,в))
 для заданной стальной балки, квадратного сечения подбираем размер «а», из условия прочности по нормальным напряжениям при изгибе, если [σ] = =160Мпа, по формуле: [σ] = [M]max / WX; (5)
для заданной стальной балки, квадратного сечения подбираем размер «а», из условия прочности по нормальным напряжениям при изгибе, если [σ] = =160Мпа, по формуле: [σ] = [M]max / WX; (5)
WX = [M]max / [σ], где WX = а3 / 6 для квадратного сечения, и отсюда найдем «а» - сторону квадрата.Из построения эпюры видно, что Мmax = 11 кН х м,определяем размер «а» квадратного сечения
WX = 11х 103 / 160 х 106 = 69 х 10-5м3, а = 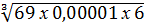 = 160мм.
= 160мм.
К задаче № 6
Кручение
Это такой вид деформации, при котором возникает в поперечном сечении бруса единственный внутренний силовой фактор – крутящий момент Мк. Деформации кручения или сдвига возникают, если к брусу приложить пары сил m или T (Рисунок 9). Моменты этих пар называют вращающими или скручивающими. Деформация кручения круглого цилиндра (вала) заключается в повороте поперечных сечений относительно друг друга вокруг оси кручения, причем углы поворота (углы закручивания) φ прямо пропорциональны расстояниям от закрепленного сечения z или z + dz
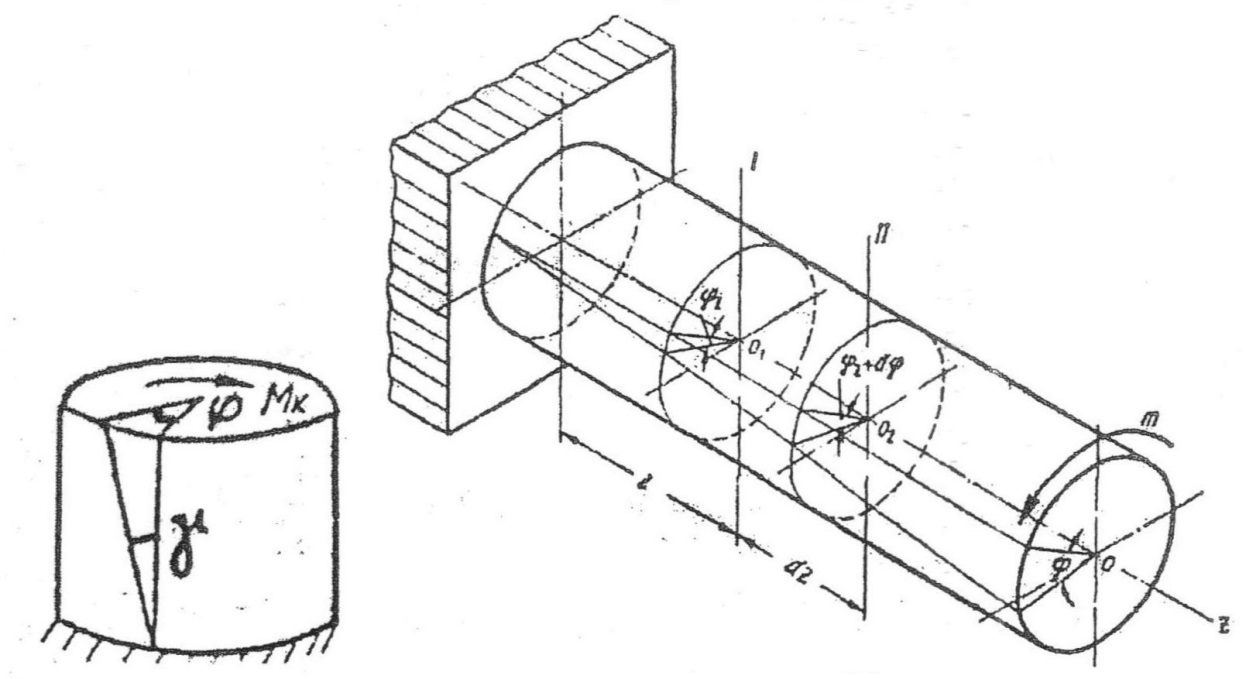
Рисунок 9-Рисунок, поясняющий деформацию кручения
При сдвиге и кручении справедлив закон Гука: τ = Gγ. При кручении в поперечном сечении бруса возникают только касательные напряжения (Рисунок 10). Распределение напряжений по сечению бруса с учетом расстояния от его центра показано на (Рисунке 11,а)-сплошной вал; 11,б)-полый вал)

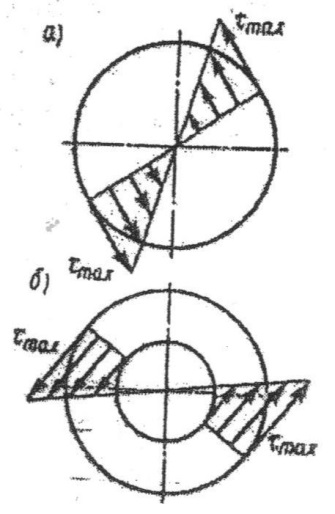
Рисунок10-Касательные Рисунок11-Распределение напряжений напряжения при кручении. по сечению бруса
Если радиус r = 0, то напряжение τ = 0. Напряжение наибольшее при наибольшем удалении от центра вала. Максимальные касательные напряжения определяются по формуле (6), см. ниже:
Формула (6):

Расчеты на прочность при кручении проводят по формуле (6):

Пример №6
На распределительном валу (Рисунок 12) установлено четыре шкива, на вал через шкив 1 подается мощность 12кВт, которая через шкивы 2, 3, 4 передается потребителю; мощности распределяются следующим образом: Р2 = 8кВт, Р3 = 3кВт, Р4 = 1кВт, вал вращается с постоянной скоростью ω = 25рад/сек.
Построить эпюру крутящих моментов на валу. Определить диаметр вала на каждом из участков бруса. Для материала вала (Сталь Ст.3), принять допускаемое напряжение при кручении [σ] = 40 МПа.

Рисунок 12-Распределительный вал с четырьмя шкивами
Решение:
1. Определяем моменты пар сил на шкивах.
Вращающий момент определяем из формулы мощности при вращательном движении Р = mω, (6)
откуда: m = P/ω.
Момент на шкиве 1 движущий, а моменты на шкивах 2, 3, 4 — моменты сопротивления механизмов, поэтому они имеют противоположное направление. Брус скручивается между движущим моментом и моментами сопротивления. При равновесии момент движущий равен сумме моментов сопротивления:
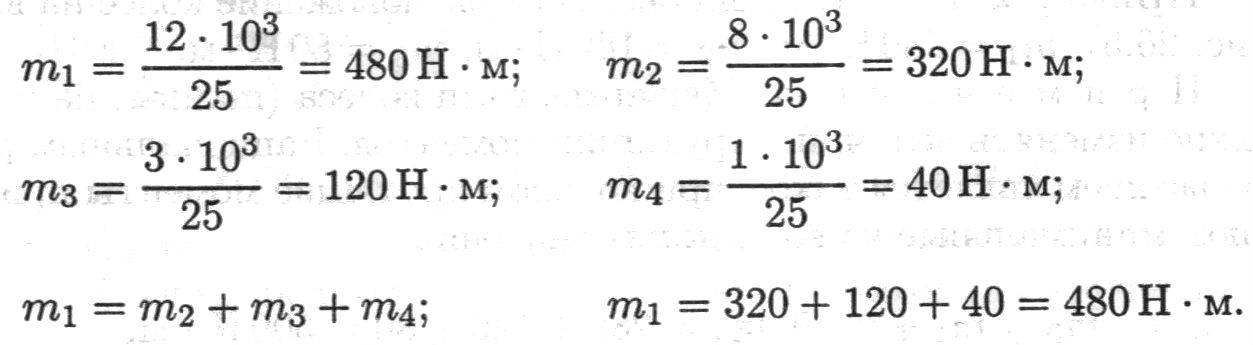
2.Определяем крутящие моменты в поперечных сечениях бруса с помощью метода сечений.
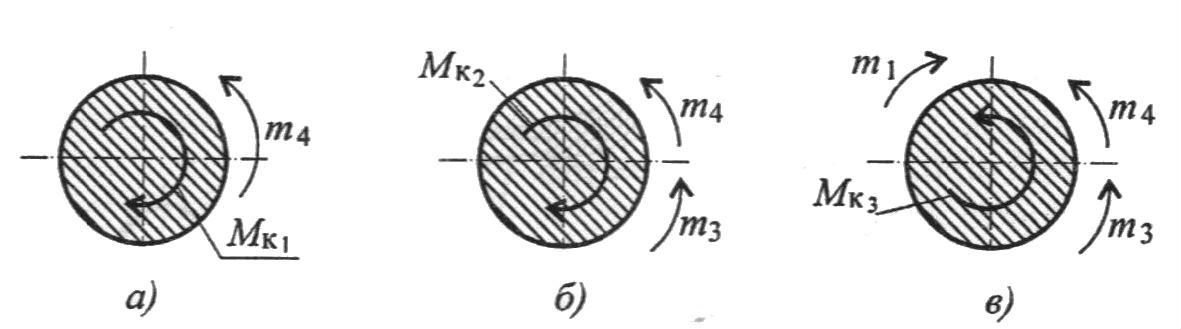
Рисунок 13- Рисунок, поясняющий определение знаков крутящих моментов
Рассматриваем последовательно все сечения бруса:
Сечение I (Рисунок 13, а)):
- m 4 + М К1 = 0; М К2 = m 4; М К1 = 40Нм – крутящий момент отрицательный.
Сечение II (Рисунок 13, б)):
-m 4 – m 3 + М К2 = 0; МК2 = m 4 + m 3; М К2 = 40 +120 = 160Нм – крутящий момент отрицательный.
Сечение III (Рисунок 13, в)):
- m 4 –m3 + m1 - M R3 = 0; -МК3 = m 4 + m 3 – m 1;
-М К3 = 40 + 120 – 480; МК3 = 320Нм –крутящий момент положительный.
Сечение IV:
МК4 = - m 4 – m 3 + m 1 – m 2 =0/
3.Cтроим эпюру крутящих моментов. Заметим, что скачок на эпюре всегда численно равен приложенному вращательному моменту.
Выбираем соответствующий масштаб.
Откладываем значения моментов, штрихуем эпюру поперек, обводим по контуру, записываем значения моментов(см. эпюру под сх






 Рисунок 1, б)-Аналитический метод решения задачи, Рисунок 1, в)- Графический метод решения задачи
Рисунок 1, б)-Аналитический метод решения задачи, Рисунок 1, в)- Графический метод решения задачи q – интенсивность нагрузки, Н/м.
q – интенсивность нагрузки, Н/м.






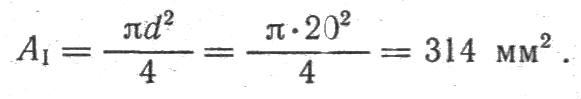
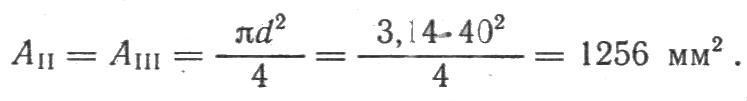

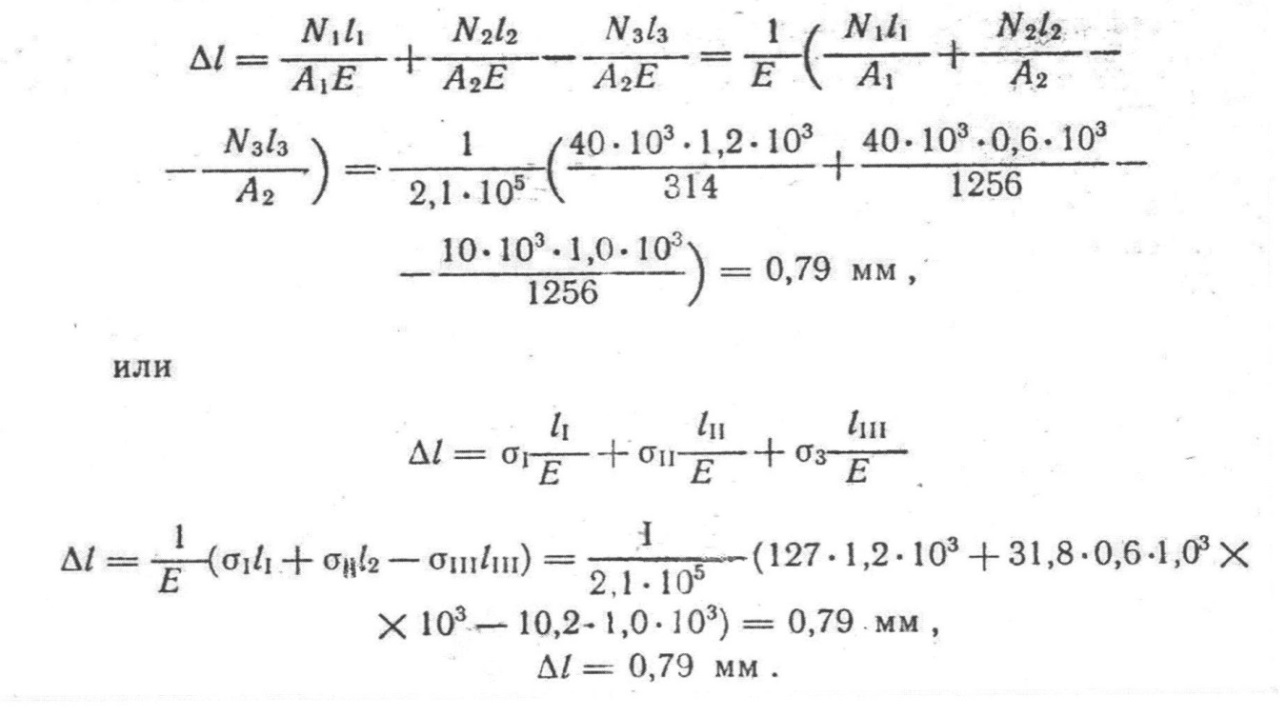


 = 160 Мпа.
= 160 Мпа.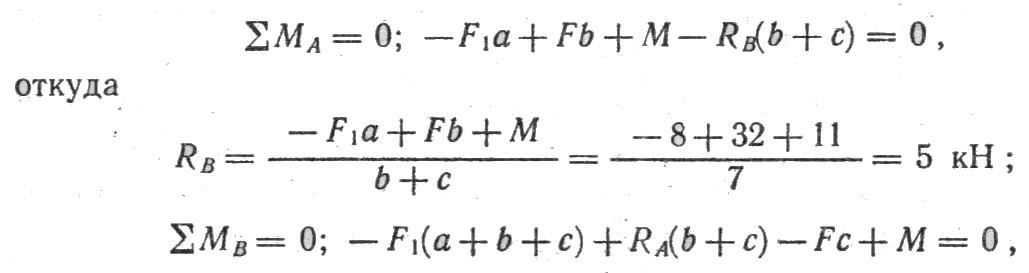
 Строим эпюру поперечных сил (Рисунок 8,б))
Строим эпюру поперечных сил (Рисунок 8,б))
 для заданной стальной балки, квадратного сечения подбираем размер «а», из условия прочности по нормальным напряжениям при изгибе, если [σ] = =160Мпа, по формуле: [σ] = [M]max / WX; (5)
для заданной стальной балки, квадратного сечения подбираем размер «а», из условия прочности по нормальным напряжениям при изгибе, если [σ] = =160Мпа, по формуле: [σ] = [M]max / WX; (5)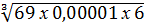 = 160мм.
= 160мм.