1 Цель работы:
1.1 изучение функций MatLab для моделирования линейных систем;
1.2 синтез передаточной функции фильтра в MathLab;
1.3 исследование свойств фильтра.
2 Литература:
2.1 Оппенгейм А., Шафер Р. Цифровая обработка сигналов. Издание 3-е, исправленное. — Москва: Техносфера 2012 г.— 1048 с.
2.2 Умняшкин С. В. Теоретические основы цифровой обработки и представления сигналов: Учебное пособие. — Москва: Техносфера 2012 г.— 368 с. — Электронное издание.
2.3 Солонина А.И., Клионский Д.М., Меркучева Т.В., Перов С.Н. Цифровая обработка сигналов и MATLAB. — Санкт-Петербург: БХВ-Петербург 2013 г.— 512 с.
2.4 Солонина А.И. Цифровая обработка сигналов. Моделирование в Simulink. — Санкт-Петербург: БХВ-Петербург 2012 г.— 432 с. — Электронное издание.
3 Основное оборудование:
3.2. Персональный компьютер.
4 Подготовка к работе:
4.1 Аналоговые линейные системы
Связь между входным X(t) и выходным Y(t) сигналами некоторой аналоговой системы называется функцией преобразования
Y(t)=F[X(t)]. (1)
Линейными называют системы, для которых выполняется принцип суперпозиции: реакция на линейную комбинацию сигналов равна линейной комбинации реакций на эти сигналы, поданные на вход по отдельности.
F[X1(t)+X2(t)]=F[X1(t)]+F[X2(t)]. (2)
F[C×X(t)]=C×F[X(t)], где С=const. (3)
Реакция на d-импульс называется импульсной характеристикой системы – h(t). Физически реализуемые системы удовлетворяют двум условиям
h(t)=0 при t<0 и 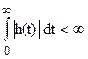 . (4)
. (4)
Реакция системы на единичное ступенчатое воздействие называется переходной характеристикой h1(t). Переходная характеристика связана с импульсной характеристикой зависимостью 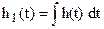 .
.
Импульсная и переходная характеристика системы позволяют определить реакцию системы на произвольный входной сигнал (в соответствии с интегралом Дюамеля).
Для анализа системы применяются также преобразование Лапласа и преобразование Фурье
 , (5)
, (5)
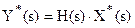 , (6)
, (6)
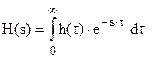 ,
, 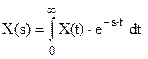 . (7)
. (7)
где Y*(s), X*(s) – изображения сигналов (преобразования Лапласа сигналов);
H(s) – передаточная функция системы.
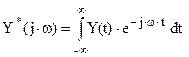 ,
,  , (8)
, (8)
 , (9)
, (9)
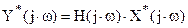 . (10)
. (10)
где Y*(j×w), X*(j×w) – изображения сигналов (преобразования Фурье сигналов);
H(j×w) – частотная характеристика системы (зависимость выходного сигнала при воздействии входного гармонического сигнала от частоты);
H(w), j(w) – амплитудно-частотная и фазо-частотная характеристики.
Частотная характеристика системы может быть определена по передаточной функции путем подстановки 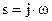 .
.
Для линейной системы выполняется принцип суперпозиции
Y*(s)=H(s)×X1*(s)+H(s)×X2*(s)= H(s)×[X1*(s)+X2*(s) ], (11)
Y*(s)=C×H(s)×X*(s)=H(s)×C×X*(s). (12)
При последовательном / параллельном соединении линейных систем общая передаточная функция равна произведению / сумме передаточных функций этих систем
H*(s)=H1(s)×H2(s), (13)
H*(s)=H1(s)+H2(s). (14)
В том случае, если при проектировании системы заданы требования в частотной области, прежде всего, производится расчет передаточной функции (частотной характеристики) системы. По передаточной функции далее можно определить импульсную (переходную) характеристику системы.
Например, во многих случаях полученная передаточная функция системы H(s) может быть представлена в дробно-рациональной форме
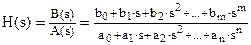 , (15)
, (15)
причем m<n и коэффициенты ai, bi – действительные числа.
Вычислив корни знаменателя A(s), т.е. полюса системы spi, можно представить передаточную функцию в виде
 , (16)
, (16)
где ki – кратность корней.
В случае, если все полюса простые (ki=1), импульсная характеристика системы определяется выражением
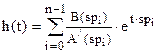 , t > 0. (17)
, t > 0. (17)
Переходная характеристика определяется в этом случае выражением
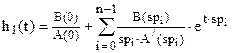 , t > 0. (18)
, t > 0. (18)
4.2 Функции Simulink для моделирования аналоговых линейных систем
Работа в программе MatLab осуществляется с помощью симулятора работы виртуального прибора Simulink. Пакет Simulink позволяет осуществлять исследование (моделирование) поведения динамических систем. Запуск пакета Simulink можно произвести из командного окна MatLab, нажавпентаграмму  в панели инструментов и открыв новую модель (пиктограмма
в панели инструментов и открыв новую модель (пиктограмма  ).
).
При запуске Simulink открываются два окна: пустое окно untitled (окно для создания блок–диаграммы модели) и окно Library Simulink (библиотека) с перечнем основных разделов библиотеки.
В открывшееся окно untitled необходимо добавить блоки, моделирующие работу источников сигналов, измерительных приборов и аналоговых систем.
4.2.1 Для моделирования работы аналогового фильтра требуется составить следующую структурную схему (модель), рис. 1.
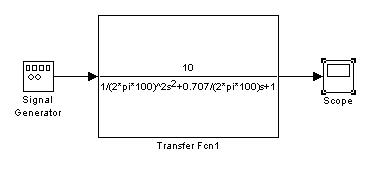
Рис. 1. Структурная схема аналогового фильтра.
Сигналы в модели передаются по линиям. Линия соединяет выходной порт одного блока с входным портом другого блока. Линия может также разветвляться и соединять выходной порт одного блока с выходными портами нескольких блоков. Любая линия связи может иметь произвольное число ответвлений, начало каждого из которых обозначается точкой.
Чтобы соединить выходной порт одного блока с входным портом другого, нужно выполнить следующие действия:
· установить указатель мыши на выходной порт первого блока (при этом курсор должен принять форму перекрестия);
· нажать левую кнопку мыши и, удерживая ее в этом положении, передвинуть указатель к входному порту второго блока;
· отпустить кнопку мыши.
Линии можно нарисовать как от входного порта к выходному, так и наоборот.
4.2.2. Моделирование работы аналогового фильтра низких частот может быть выполнено с помощью блока Transfer Fcn (Simulink / Continuous / Transfer Fcn).
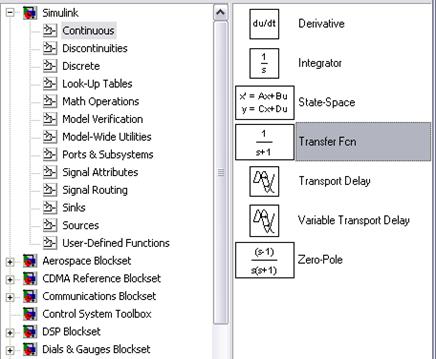
Рис. 2. Расположение блока Transfer Fcn
В блоке Transfer Fcn в качестве исходных данных берется описание передаточной функции H(s) системы в операторной форме. Передаточная функция H(s) задаётся в блоке параметров фильтра, который вызывается двойным щелчком на пиктограмму фильтра  ,
,
где Numerator – это значения коэффициентов числителя В, а Denominator – значения коэффициентов знаменателя А (коэффициенты вводятся через пробел, начиная с коэффициента с наибольшим индексом).

Рис. 3. Блок параметров фильтра Transfer Fcn
4.2.3. Для задания гармонического сигнала, используется блок Signal Generator (Simulink/ Sources/Signal Generator), рис. 4.а.
Параметры сигнала задаются в блоке параметров Signal Generator (рис. 4.б), который вызывается двойным щелчком на пиктограмму Signal Generator ( ). В графе Wave form задается форма сигнала: sine – синусоидальный сигнал, square – прямоугольный сигнал, saw tooth – пилообразный сигнал, random – случайный сигнал (шум). В графах Amplitude и Frequency задается амплитуда и частота сигнала. В графе Units задается единица измерения, в которых задана частота (Hertz – Герцы или rad/sec – рад/ сек.).
). В графе Wave form задается форма сигнала: sine – синусоидальный сигнал, square – прямоугольный сигнал, saw tooth – пилообразный сигнал, random – случайный сигнал (шум). В графах Amplitude и Frequency задается амплитуда и частота сигнала. В графе Units задается единица измерения, в которых задана частота (Hertz – Герцы или rad/sec – рад/ сек.).

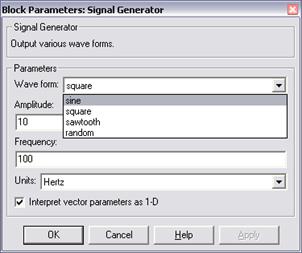
а) б)
Рис. 4. Расположение блока Signal Generator (а) и окно настройки его параметров (б)
4.2.4. Для того, чтобы на вход системы подать постоянное ступенчатое воздействие, используется блок Constant (Simulink/ Sources/ Constant),рис. 5. Реакция системы на данный сигнал является переходной характеристикой системы.

Рис. 5. Расположение блока Constant
4.2.5. Для визуального просмотра сигналов используют блоки, которые при моделировании играют роль смотровых окон; к ним также относится блок Scope( осциллограф ) (Simulink /Sinks / Scope), рис 6.
Блок Scope имеет один вход и позволяет в процессе моделирования наблюдать интересующие пользователя процессы. Чтобы просмотреть сигнал, нужно дважды щелкнуть мышью на пиктограмму  .
.
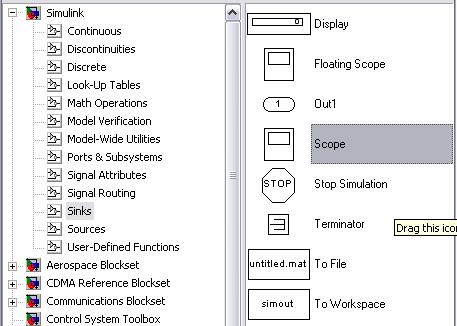
Рис. 6. Расположение блока Scope
Основным параметром осциллографа является количество входов (т.е. количество отображаемых сигналов, одновременно в окне может отображаться до 30 сигналов). В зависимости от количества сигналов осциллограф может иметь несколько экранов. Экран осциллографа с двумя входами выглядит так, как показано на рис. 7.а (пиктограмма выглядит так  ).
).


а) б)
Рис. 7. Экран осциллографа Scope с двумя входами (а) и окно настройки параметров
Для управления параметрами графиков и выполнения над ними различных действий в окне имеется панель инструментов, содержащая несколько пиктограмм со следующими назначениями:
 печать содержимого окна Scope;
печать содержимого окна Scope;
 вызов окна настройки параметров блока Scope;
вызов окна настройки параметров блока Scope;
 изменение масштаба осей графиков;
изменение масштаба осей графиков;
 изменение масштаба по горизонтальной оси;
изменение масштаба по горизонтальной оси;
 изменение масштаба по вертикальной оси;
изменение масштаба по вертикальной оси;
 автоматическая установка оптимального масштаба осей (автошкала);
автоматическая установка оптимального масштаба осей (автошкала);
 сохранение установленного масштаба осей.
сохранение установленного масштаба осей.
Нажатие пиктограммы  приводит к появлению окна настройки параметров Scope (Scope parameters), рис. 7.б.
приводит к появлению окна настройки параметров Scope (Scope parameters), рис. 7.б.
В графе Number of axes задается количество входов осциллографа, Time range – верхний предел времени, отображаемого на оси абсцисс, Tick labels – отображение осей координат (all – все оси, none – нет осей, bottom axis only – только горизонтальная ось). Рекомендуется использовать настройки, выставленные по умолчанию.
4.3 Режимы моделирования систем в программе Simulink (меню Simulation)
Не смотря на то, что меню Simulation ( моделирование) содержит всего несколько команд (рис. 8), именно они играют основную роль при проведении исследований модели. Посредством этих команд разработчик получает возможность не только динамически управлять сеансом моделирования, но и изменять многие важнейшие параметры модели, такие, например, как способ изменения модельного времени, алгоритм расчета и формат представления результатов моделирования.
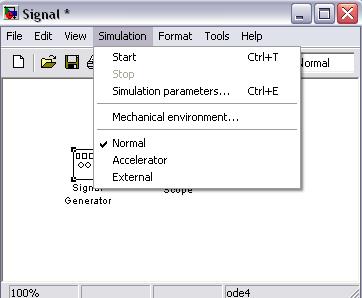
Рис. 8. Меню Simulation.
Рассмотрим подробнее средства управления моделью и параметрами сеанса моделирования, которые предоставляет исследователю окно Simulation Parameters (параметры моделирования), рис 9. Элементы управления на вкладке Solver собраны в три группы.
Simulation time (интервал моделирования) – выбор интервала моделирования посредством указания начального (Start time) и конечного (Stop time) значений модельного времени.
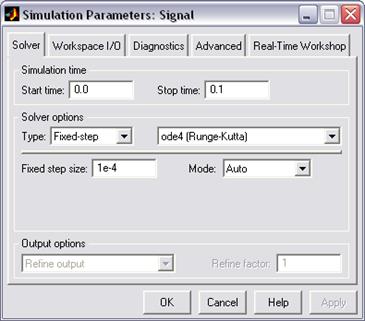
Рис. 9. Окно установки параметров моделирования.
Solver options (параметры расчета) – выбор метода реализации (расчета) модели.
Output options (параметры вывода) – параметры вывода выходных параметров моделируемой системы (при моделировании с переменным шагом).
Под выбором метода реализации модели имеется в виду следующее. Имея структуру исследуемой системы в виде блок–диаграммы, разработчик может выбрать метод отображения хода моделирования. С помощью двух раскладывающихся списков Type (Тип) система может быть реализована в следующих формах:
· с дискретными состояниями и дискретным временем перехода из одного состояния в другое;
· с дискретными состояниями и непрерывным временем перехода;
· с непрерывными состояниями и дискретным временем переходов;
· с непрерывными состояниями и непрерывным временем переходов.
Первый список (слева) позволяет выбрать способ изменения модельного времени:
· Variable – step (переменный шаг) – моделирование с переменным шагом;
· Fixed – step (фиксированный шаг) – моделирование с фиксированным шагом.
Второй список (справа) позволяет выбрать метод расчета нового состояния системы. Первый вариант (discrete) обеспечивает расчет дискретных состояний системы. Остальные пункты списка обеспечивают выбор метода расчета нового состояния для непрерывных систем. Эти методы различаются для переменного (Variable – step) и для фиксированного (Fixed – step) шага времени, но основаны на единой методике – решение обыкновенных дифференциальных уравнений(ode).
Ниже двух раскрывающихся списков Type находится поле, название которого изменяется в зависимости от выбранного способа изменения модельного времени (рекомендуется оставить параметры по умолчанию).
Параметры других вкладок также можно использовать по умолчанию.
5 Задание:
5.1 Изучить методы моделирования линейных систем в пакете программ MatLab.
5.2 Синтезировать передаточную функцию аналоговой линейной системы.
5.3 Найти переходную характеристику фильтра и время установления.
5.4 Найти отклики фильтра на гармонические сигналы в полосе пропускания и полосе задерживания, оценить избирательные свойства фильтра.
5.5 Сравнить результаты расчетов с данными, полученными при моделировании аналогичной системы в пакете программ Mathcad
Порядок выполнения
6.1 Создать модель фильтра (п. 4.2.1) в программе Simulink.
Подготовить и ввести в программу исходные данные (п. 4.2.2) в соответствии с заданным вариантом (по номеру компьютера), необходимые для синтеза аналогового ФНЧ: аппроксимация – по Баттерворту; частота среза Fс; коэффициент усиления K0;
порядок фильтра N=2.
| Вариант
|
|
|
|
|
|
|
| Fс
| 100 Гц
| 200 Гц
| 300 Гц
| 400 Гц
| 500 Гц
| 600 Гц
|
| K0
|
|
|
|
|
|
|
ФНЧ Баттерворта второго порядка определяется следующим образом:
 , где B0=K0, A0=1,
, где B0=K0, A0=1,  ,
,  .
.
6.2 Подать на вход ФНЧ единичное ступенчатое воздействие (п. 4.2.4). Вычислить переходную характеристику системы h1(t). Построить графики входного ступенчатого воздействия и переходной характеристики на экране осциллографа Scope (п. 4.2.5).
6.3 Определить время установления tуст выходного сигнала на уровне 95 % (или 105 % при наличии колебательного переходного процесса). Сравнить полученный график и значение tуст с данными, полученными при моделировании системы в программе Mathcad.
6.4 Выбрать в качестве входного гармонический сигнал X(t) с частотой Fx равной частоте среза фильтра Fc и единичной амплитудой (п. 4.2.3). Построить графики входного X(t) и выходного сигнала Y(t) (п. 4.2.5).
Повторить п.6.3 для гармонического сигнала с частотой Fx=2×Fc.
7 Содержание отчета:
7.1 Название и цель работы
7.2 Листинг выполненных программ согласно пункту 5 с описание команд
7.4 Выводы по полученным результатам
7.3 Ответы на контрольные вопросы
8 Контрольные вопросы:
8.1 Свойства d-импульса и прямоугольного ступенчатого сигнала.
8.2 Что такое импульсная и переходная характеристика системы. Взаимосвязь импульсной и переходной характеристик.
8.3 Что такое передаточная функция и частотная системы.
8.4 Взаимосвязь импульсной характеристики и передаточной функции системы.
8.5 Как определяются время установления системы и частоты среза АЧХ.
8.6 Указать где и в каком порядке должны быть введены значения в блоке параметров фильтра Transfer Fcn, если передаточная функция
 .
.
8.7 Каким образом можно одновременно проанализировать три сигнала с разных источников.
8.8 Как задать интервал времени моделирования в программе Simulink.
8.9 Какие блоки программы Simulink используются для создания гармонических сигналов, ступенчатых воздействий, прямоугольных и треугольных импульсов.
Лабораторная работа 3
Генерация сигналов в MatLab
1 Цель работы:
1.1 Изучение средств системы по генерации сигналов, разложению их в ряд Фурье и дискретному преобразованию Фурье, приобретение практических навыков их использования
2 Литература:
2.1 Оппенгейм А., Шафер Р. Цифровая обработка сигналов. Издание 3-е, исправленное. — Москва: Техносфера 2012 г.— 1048 с.
2.2 Умняшкин С. В. Теоретические основы цифровой обработки и представления сигналов: Учебное пособие. — Москва: Техносфера 2012 г.— 368 с. — Электронное издание.
2.3 Солонина А.И., Клионский Д.М., Меркучева Т.В., Перов С.Н. Цифровая обработка сигналов и MATLAB. — Санкт-Петербург: БХВ-Петербург 2013 г.— 512 с.
2.4 Солонина А.И. Цифровая обработка сигналов. Моделирование в Simulink. — Санкт-Петербург: БХВ-Петербург 2012 г.— 432 с. — Электронное издание.
3 Основное оборудование:
3.2. Персональный компьютер.
4 Подготовка к работе:
Сигнал может быть:
 Аналоговый – исходный физический сигнал, являющийся непрерывной функцией времени;
Аналоговый – исходный физический сигнал, являющийся непрерывной функцией времени;

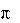
 Дискретный – результат преобразования аналогового сигнала в последовательность чисел, которые являются значениями сигнала в отдельные (дискретные) моменты времени, называются отсчетами. Как правило, отсчеты берутся через равные промежутки времени т, называемые периодом дискретизации. Величина, обратная периоду дискретизации, называется частотой дискретизации: fd = 1/t. Круговая частота определяется, как d = 2 /t;
Дискретный – результат преобразования аналогового сигнала в последовательность чисел, которые являются значениями сигнала в отдельные (дискретные) моменты времени, называются отсчетами. Как правило, отсчеты берутся через равные промежутки времени т, называемые периодом дискретизации. Величина, обратная периоду дискретизации, называется частотой дискретизации: fd = 1/t. Круговая частота определяется, как d = 2 /t;
 Цифровой; в вычислительных устройствах отсчеты сигнала представляются в виде двоичных чисел. Процесс преобразования отсчетов в числа называется квантованием по уровню, а возникшие при этом ошибки – ошибками
Цифровой; в вычислительных устройствах отсчеты сигнала представляются в виде двоичных чисел. Процесс преобразования отсчетов в числа называется квантованием по уровню, а возникшие при этом ошибки – ошибками
или шумами квантования. Сигнал, дискретный во времени и квантованный по уровню, называют цифровым.
Для того, чтобы гармонический сигнал мог быть адекватно представлен дискретными отсчетами, его частота не должна превышать половины частоты дискретизации: fN = fD/2. Эта частота называется частотой Найквиста.
Дискретный сигнал представляет собой последовательность чисел,
поэтому для его расчета формируют вектор опорных значений времени. Для этого удобно задавать значение частоты дискретизации Fs и использовать обратную величину частоты дискретизации в качестве шага временного ряда.
Пример 1. Сформировать затухающий гармонический сигнал:
>> Fs = 8e3; % частота дискретизации 8 кГц
>> t = 0:1/Fs:1; % одна секунда дискретных значений времени
>> A = 2; % амплитуда – два вольта
>> f0 = 1e3; % частота гармонического сигнала 1кГц
>> phi = pi/4; % начальная фаза гармонического сигнала – 45˚
>> s1 = A*cos(2*pi*f0*t+phi); % гармонический сигнал
>> alpha = 1e3; % скорость затухания
>> s2 = exp(–alpha*t).*s1; % затухающая синусоида
% вывод (визуализация) затухающей синусоиды различными способами
>> figure,subplot(2,2,1);plot(s2(1:100))
>> subplot(2,2,2);plot(s2(1:100),'.')
>> subplot(2,2,3);stem(s2(1:100))
>> subplot(2,2,4);stairs(s2(1:100))
Функции генерации дискретных сигналов
Функции генерации одиночных импульсов
В пакете Signal Processing системы MatLab имеются функции, генерирующие часто встречаемые на практике непериодические сигналы:
rectpuls – прямоугольный импульс вида
rect(t)
1, t 1




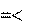 2;
2;

 0, t
0, t
sinc– импульс вида sin c(t)
sin(t);





t
tripuls – треугольный импульс вида
(t)
Прямоугольный импульс
Синтаксис
y = rectpuls(t,width),
где t – вектор значений времени;, width – ширина (длительность) импульса (по умолчанию width = 1, в этом случае функция rectpuls производит результат, соответствующий математической функции rect).
Пример 2. Сформировать прямоугольный импульс:
>> t = –0.6:0.01:1;
>> y = rectpuls(t);
>> figure,plot(t,y);
>> ylim([0 1.5])
Пример 3. Сформировать пару разнополярных прямоугольных импульсов с амплитудой 5 В и длительностью 20 мс, расположенных справа и слева от начала отсчета времени:
>> fs = 1e3;
>> t = –40e–3:1/Fs:40e–3;
>> T = 20e–3;
>> A = 5;
>> s = –A*rectpuls(t+T/2,T) = A*rectpuls(t–T/2,T);
>> figure,plot(t,s)
>> ylim([–6 6])
Функция Дирака
Наибольший интерес в теоретическом отношении представляет предельный случай прямоугольного импульса, когда его длительность стремится к нулю, а высота импульса стремится к бесконечности. В этом случае в результате предельного перехода получаем новую функцию с необычайными свойствами. Она называется «дельта-функция», или функция Дирака. Эта функция обладает следующими свойствами:
1) Она равна нулю при t < 0 и t > 0 и бесконечна в точке t = 0:


 (t) 0, t 0;
(t) 0, t 0;
, t 0
 (t)dt 1
(t)dt 1
2).

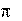 Импульс с ограниченной полосой частот
Импульс с ограниченной полосой частот
Для формирования импульса вида sin(
Синтаксис y = sinc(t),
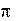 где t – вектор значений времени.
где t – вектор значений времени.
t) /)
t используется функция sinc:
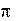 Пример 4. Сформировать импульс вида sin(
Пример 4. Сформировать импульс вида sin(
>> f = –10:0.1:10;
>> y = sinc(f);
>> figure,plot(f,y);
>> ylim([–2 2])
t) /(
t):
Треугольный импульс
Для формирования треугольного импульса с единичной амплитудой служит функция tripuls:
Синтаксис
y = tripuls(t,width,skew),
где t – вектор значений времени; width – ширина (width = 1 по умолчанию) импульса; skew – коэффициент асимметрии импульса, определяющий положение его вершины.
Пик импульса расположен при t = width*skew/2, параметр skew должен лежать в диапазоне от –1 до 1 (skew = 0 по умолчанию).
Пример 5. Сформировать симметричный трапециевидный импульс с амплитудой 10 В и размерами верхнего и нижнего оснований 20 и 60 мс соответственно. Частота дискретизации 1кГц:
>> Fs = 1e3;
>> t = –50e–3:1/Fs:50e–3;
>> A = 10;
>> T1 = 20e–3;
>> T2 = 60e–3;
>> s = A*(T2*tripuls(t,T2)–T1*tripuls(t,T1))/(T2–T1);
>> figure,plot(t,s)
Функции генерации последовательности импульсов
Функция формирования конечной последовательности импульсов pulstran
Для генерации конечной последовательности импульсов одинаковой формы с произвольно задаваемыми задержками и уровнями служит функция pulstran.
Синтаксис
y = pulstran(t, d, ‘func’, p1, p2, …) y = pulstran(t, d, p, fs, 'method')
Сами импульсы могут задаваться одним из двух способов:
1) Именем функции, генерирующей импульс;
2) Рассчитанным вектором отсчетов, с помощью которого задается форма импульса.
Для первого способа функция вызывается следующим образом: y = pulstran(t, d, ‘func’, p1, p2, …),
где t – вектор значений времени; d – вектор задержек (если d – двухстолбцовая матрица, то первый столбец трактуется как задержки импульсов, а второй – как их уровни); ‘func’ – имя функции, генерирующей одиночный импульс; оставшиеся параметры – p1, p2, … – дополнительные.
Пример 6. Сформировать пять симметричных треугольных импульсов, интервалы между которыми линейно увеличиваются, а амплитуды экспоненциально уменьшаются:
>> Fs = 1e3; % частота дискретизации
>> t = 0:1/Fs:0.5; % дискретное время
>> tau = 20e–3; % длительность импульса
>> d = [20 80 160 260 380]'*1e–3; % задержки импульсов
>> d(:,2) = 0.8.^(0:4)'; % амплитуды импульсов
>> y = pulstran(t,d,'tripuls',tau);
>> figure,plot(t,y);
Для второго способа надо рассчитать вектор отсчетов импульса и вызвать функцию следующим образом:
y = pulstran(t, d, p, fs, 'method').
Смысл входных параметров t и d тот же, что и раньше. Вектор р должен содержать отсчеты одиночного импульса, а параметр fs указывает частоту дискретизации, использованную при расчете этого вектора. Считается, что первый отсчет из вектора р соответствует нулевому моменту времени. Так как частота fs может не совпадать с шагом значений вектора t, и задержки из вектора d тоже не обязательно кратны этому шагу, для пересчета задержанных импульсов к сетке моментов времени t в общем случае надо задавать интерполяцию. Метод интерполяции задается в параметре 'method'. Он может принимать следующие значения: 'nearest', 'linear', 'cubic', 'v5cubic', 'spine', 'chip'. По умолчанию fs= 1 и 'method' = 'linear'.
Пример 7. Сформировать последовательность из 6 импульсов, имеющих форму одного периода функции sin(t)2. Длительность импульсов равна 60 мс, частота его дискретизации составляет 400 Гц. Расстояние между центрами
импульсов будет равным 64 мс, а частота дискретизации выходного сигнала составляет 1 кГц. Импульсы будут затухать с ростом номера.
>> % Генерация вектора отсчетов одиночного импульса
>> Fs0 = 400; %частота дискретизации импульсов
>> tau = 60e–3; % длительность импульсов
>> t0 = 0:1/Fs0:tau; % дискретное время для импульса
>> s0 = sin(pi*t0/tau).^2; % вектор отсчетов импульса
>> % Генерация последовательности импульсов
>> Fs = 1e3;
>> t = 0:1/Fs:0.5;
>> d = (1:6)'*64e–3;
>> d(:,2) = 0.6.^(0:5)'
>> y = pulstran(t,d,s0,Fs0);
>> figure,plot(t,y)
Функция формования последовательности прямоугольных импульсов square
Для генерации последовательности прямоугольных импульсов служит функция square:
Синтаксис
y = square(t,duty),
где t – вектор значений времени; duty – коэффициент заполнения – величина, обратная скважности (в процентах), т. е. отношение длительности импульса к периоду. По умолчанию duty = 50, т. е. генерируется меандр.
Пример 8. Сформировать однополярные прямоугольные импульсы с амплитудой 3 В, частотой следования 50 Гц и длительностью 5 мс.
>> Fs = 1e3; % частота дискретизации
>> t = –10e–3:1/Fs:50e–3; % дискретное время
>> A = 3; % амплитуда
>> f0 = 50; % частота следования импульсов
>> tau = 5e–3; % длительность импульсов
>> s = (square(2*pi*t*f0,f0*tau*100)+1)*A/2;
>> figure,plot(t,s);
>> ylim([0 5])
Ряд Фурье
Разложению в ряд Фурье могут подвергаться периодические сигналы. При этом они представляются в виде суммы гармонических функций либо комплексных экспонент с частотами, образующими арифметическую прогрессию. Для того, чтобы такое разложение существовало, фрагмент сигнала длительностью в один период должен удовлетворять условиям Дирихле:
1. Не должно быть разрывов второго рода (с уходящими в бесконечность ветвями функции);
2. Число разрывов первого рода (скачков) должно быть конечным;
3. Число экстремумов должно быть конечным.
Существует несколько форм представления: синусно-косинусная, вещественная, комплексная.

 Представим синусно-косинусную форму ряда Фурье:
Представим синусно-косинусную форму ряда Фурье:
s(t)
(akcos(k

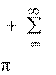

 k 1
k 1
1t)
bk sin(k
1t)), (1)
 где 1
где 1
2 / T
– круговая частота, кратные ей частоты k
1 называются
гармониками.
Коэффициенты ряда ak
и bk
рассчитываются по формулам (2), (3):
 ak 2 T
ak 2 T
 bk 2 T
bk 2 T
T / 2
 s(t) cos(k
s(t) cos(k
T / 2
 T / 2
T / 2
s(t) sin(k
T / 2
1t)dt; (2)
1t)dt. (3)
Слагаемое с константой a 0
представляет собой среднее сигнала на
периоде, рассчитываемое по формуле (4):
 a0 1
a0 1

2 T
T / 2
 s(t)dt. (4)
s(t)dt. (4)
T / 2
Если s(t) является четной функцией, то все bkбудут равны нулю, и в фор- муле ряда Фурье будут присутствовать только косинусные слагаемые; если s(t) является нечетной функцией, то останутся только синусные слагаемые.
Совокупность амплитуд гармоник ряда Фурье называется амплитудным спектром, а совокупность их фаз – фазовым спектром.
Разложение в ряд Фурье последовательности прямоугольных импульсов
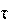 Рассмотрим последовательность прямоугольных импульсов с амплитудой А, длительностью и периодом повторения T. Начало отсчета времени возьмем расположенным в середине импульса. Данный сигнал является четной функцией, и при разложении его в ряд Фурье будут присутствовать только
Рассмотрим последовательность прямоугольных импульсов с амплитудой А, длительностью и периодом повторения T. Начало отсчета времени возьмем расположенным в середине импульса. Данный сигнал является четной функцией, и при разложении его в ряд Фурье будут присутствовать только
косинусные слагаемые
ak, равные
 ak 2
ak 2
/ 2 A cos(2 k t)dt
2A sin(2).
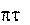


 T / 2 T k T
T / 2 T k T

 Отношение периода к длительности импульсов называется скважностью
Отношение периода к длительности импульсов называется скважностью
последовательности импульсов q
T /. Если ввести этот параметр в формулу
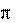 для коэффициента ряда Фурье, а затем привести формулу к виду получим:
для коэффициента ряда Фурье, а затем привести формулу к виду получим:
sin(x) / x,

 ak 2A sin(k)
ak 2A sin(k)
sin(k) 2A q

 .
.
k q q k
q
 Поскольку при x
Поскольку при x
sin(x) / x
1, то a0

 2
2
AA


 .
.
q T
Само представление последовательности прямоугольных импульсов в виде ряда Фурье можно записать в виде формулы:
 s(t) A
s(t) A
2A sin(k) cos(2 k t).


 q k1 k q T
q k1 k q T
 Последовательность прямоугольных импульсов со скважностью, равной двум, когда длительность импульсов и промежутки между ними равны, называется меандром. Представление меандра в виде ряда Фурье может быть записано следующим образом:
Последовательность прямоугольных импульсов со скважностью, равной двум, когда длительность импульсов и промежутки между ними равны, называется меандром. Представление меандра в виде ряда Фурье может быть записано следующим образом:
s(t)
A2A (cos(2)
1 cos(3 2)
1 cos(5 2)
...).
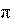

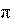

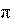

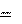
2 T 3 T 5 T
Пример 9. Получить меандр сложением отдельных гармоник:
>> N = 8; % чиcло ненулевых гармоник
>> t = –1:0.01:1; % вектор моментов времени
>> A = 1; % амплитуда
>> T = 1; % период
>> nh = (1:N)*2–1; % номера ненулевых гармоник
>> harmonics = cos(2*pi*nh'*t/T); % строки-гармоники
>> Am = 2/pi./nh; % амплитуды гармоник
>> Am(2:2:end) = –Am(2:2:end); % чередование знаков
>> s1 = harmonics.*repmat(Am',1,length(t));
>> s2 = cumsum(s1); % частичные суммы гармоник (суммирование с накоплением)
>> for k = 1:N
>> subplot(4,2,k)
>> plot(t,s2(k,:))
>> end;
Так как последовательность прямоугольных импульсов содержит скачки (разрывы 1-го рода), в окрестностях точек разрывов суммирование ряда Фурье дает наклонный участок, а на примыкающих к разрыву участках сумма ряда Фурье дает заметные пульсации. Это явление, присущее рядам Фурье для любых сигналов с разрывами 1-го рода, называется эффектом Гиббса.
Прямое и обратное преобразование Фурье
Преобразование Фурье является инструментом спектрального анализа непериодических сигналов. В системе MatLab для вычисления прямого преобразования Фурье одномерных сигналов используется функция fft:
Синтаксис
y = fft(x) – вычисляет прямое ДПФ (дискретное преобразование Фурье) для вектора х; если х – матрица, преобразование производится для каждого ее столбца по отдельности;
y = fft(x,N) – вычисляет прямое ДПФ; перед вычислением предварительно приводит исходные данные к размеру N, урезая их или дополняя нулями.
Для вычисления обратного преобразования Фурье одномерных сигналов используется функция ifft:
Синтаксис
x = ifft(y,N) – вычисляет обратное ДПФ; предварительно приводит исходные данные к размеру N, урезая их или дополняя нулями.
Для вычисления прямого ДПФ двумерного сигнала используется функция
fft2, обратн



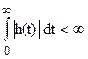 . (4)
. (4)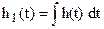 .
. , (5)
, (5)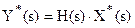 , (6)
, (6)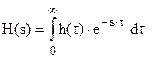 ,
, 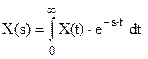 . (7)
. (7)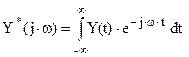 ,
,  , (8)
, (8) , (9)
, (9)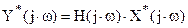 . (10)
. (10)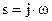 .
.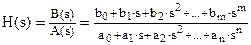 , (15)
, (15) , (16)
, (16)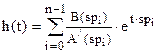 , t > 0. (17)
, t > 0. (17)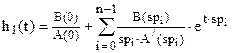 , t > 0. (18)
, t > 0. (18) в панели инструментов и открыв новую модель (пиктограмма
в панели инструментов и открыв новую модель (пиктограмма  ).
).

 ,
,
 ). В графе Wave form задается форма сигнала: sine – синусоидальный сигнал, square – прямоугольный сигнал, saw tooth – пилообразный сигнал, random – случайный сигнал (шум). В графах Amplitude и Frequency задается амплитуда и частота сигнала. В графе Units задается единица измерения, в которых задана частота (Hertz – Герцы или rad/sec – рад/ сек.).
). В графе Wave form задается форма сигнала: sine – синусоидальный сигнал, square – прямоугольный сигнал, saw tooth – пилообразный сигнал, random – случайный сигнал (шум). В графах Amplitude и Frequency задается амплитуда и частота сигнала. В графе Units задается единица измерения, в которых задана частота (Hertz – Герцы или rad/sec – рад/ сек.).


 .
.
 ).
).

 печать содержимого окна Scope;
печать содержимого окна Scope; вызов окна настройки параметров блока Scope;
вызов окна настройки параметров блока Scope; изменение масштаба осей графиков;
изменение масштаба осей графиков; изменение масштаба по горизонтальной оси;
изменение масштаба по горизонтальной оси; изменение масштаба по вертикальной оси;
изменение масштаба по вертикальной оси; автоматическая установка оптимального масштаба осей (автошкала);
автоматическая установка оптимального масштаба осей (автошкала); сохранение установленного масштаба осей.
сохранение установленного масштаба осей. приводит к появлению окна настройки параметров Scope (Scope parameters), рис. 7.б.
приводит к появлению окна настройки параметров Scope (Scope parameters), рис. 7.б.

 , где B0=K0, A0=1,
, где B0=K0, A0=1,  ,
,  .
. .
. Аналоговый – исходный физический сигнал, являющийся непрерывной функцией времени;
Аналоговый – исходный физический сигнал, являющийся непрерывной функцией времени;
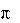




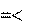 2;
2;






 (t) 0, t 0;
(t) 0, t 0; (t)dt 1
(t)dt 1
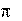 Импульс с ограниченной полосой частот
Импульс с ограниченной полосой частот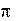 где t – вектор значений времени.
где t – вектор значений времени.
 Представим синусно-косинусную форму ряда Фурье:
Представим синусно-косинусную форму ряда Фурье:
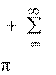
 k 1
k 1 где 1
где 1 ak 2 T
ak 2 T bk 2 T
bk 2 T s(t) cos(k
s(t) cos(k
 s(t)dt. (4)
s(t)dt. (4)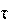 Рассмотрим последовательность прямоугольных импульсов с амплитудой А, длительностью и периодом повторения T. Начало отсчета времени возьмем расположенным в середине импульса. Данный сигнал является четной функцией, и при разложении его в ряд Фурье будут присутствовать только
Рассмотрим последовательность прямоугольных импульсов с амплитудой А, длительностью и периодом повторения T. Начало отсчета времени возьмем расположенным в середине импульса. Данный сигнал является четной функцией, и при разложении его в ряд Фурье будут присутствовать только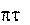


 T / 2 T k T
T / 2 T k T
 Отношение периода к длительности импульсов называется скважностью
Отношение периода к длительности импульсов называется скважностью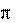 для коэффициента ряда Фурье, а затем привести формулу к виду получим:
для коэффициента ряда Фурье, а затем привести формулу к виду получим:
 ak 2A sin(k)
ak 2A sin(k) .
. Поскольку при x
Поскольку при x
 2
2



 Последовательность прямоугольных импульсов со скважностью, равной двум, когда длительность импульсов и промежутки между ними равны, называется меандром. Представление меандра в виде ряда Фурье может быть записано следующим образом:
Последовательность прямоугольных импульсов со скважностью, равной двум, когда длительность импульсов и промежутки между ними равны, называется меандром. Представление меандра в виде ряда Фурье может быть записано следующим образом: