Общие принципы работы системы Matlab

С.А. Быстров

ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ

Методические указания по выполнению лабораторных работ

для студентов очной формы обучения

на базе среднего (полного) общего образования,

обучающихся по направлению подготовки академического бакалавра

11.03.02 «Инфокоммуникационные технологии и системы связи»

(профиль «Инфокоммуникационные технологии в сервисах и услугах связи»),

в соответствии с ФГОС ВО 3 поколения.

 

Екатеринбург

 

25.02.2016

УДК 621.931

ББК 32.88-01

 

Рецензент: доктор техн. наук, профессор Б.А. Панченко

 

Быстров С. А.

Цифровая обработка сигналов: методические указания к выполнению лабораторных работ для студентов очной формы обучения на базе среднего (полного) общего образования, обучающихся по направлению подготовки академического бакалавра 11.03.02 «Инфокоммуникационные технологии и системы связи» (профиль «Инфокоммуникационные технологии в сервисах и услугах связи»), в соответствии с ФГОС ВО 3 поколения. / С. А. Быстров. – Екатеринбург: УрТИСИ СибГУТИ, 2016. – 63 с.

Методические указания по выполнению лабораторных работ по дисциплине «Цифровая обработка сигналов» предназначены для студентов очной формы обучения на базе среднего (полного) общего образования, обучающихся по направлению подготовки бакалавра 11.03.02 «Инфокоммуникационные технологии и системы связи» (профиль «Инфокоммуникационные технологии в сервисах и услугах связи»), программа академического бакалавриата.

Выполнение лабораторных работ предусматривает закрепление теоретических знаний дисциплины.

Методические указания предназначены для использования при выполнении лабораторного практикума. Выполнение лабораторных работ предполагает исследование математических сред обработки сигналов Mathcad и MatLab. Методические указания содержат список литературы для подготовки к работе, задания для выполнения, а также список контрольных вопросов для защиты лабораторной работы. К каждой лабораторной работе также предлагается приложение.

Рекомендовано НМС УрТИСИ СибГУТИ в качестве методических указаний по выполнению лабораторных работ по дисциплине «Цифровая обработка сигналов» для студентов очной формы обучения на базе среднего (полного) общего образования, обучающихся по направлению подготовки бакалавра 11.03.02 «Инфокоммуникационные технологии и системы связи» (профиль «Инфокоммуникационные технологии в сервисах и услугах связи»), в соответствии с ФГОС ВО 3 поколения.

 

УДК 537,8

ББК 32.845

 

Кафедра общепрофессиональных дисциплин

технических специальностей

 

© УрТИСИ СибГУТИ» 2016

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

 

Методические указания к выполнению лабораторных работ составлены в соответствии с утвержденной программой дисциплины «Цифровая обработка сигналов», предназначены для студентов по направлению в соответствии с ФГОС ВО 3 поколения.

Проведение лабораторных работ предусмотрено для закрепления теоретических знаний курса, получения необходимых навыков работы с компьютерными программами.

Перед выполнением лабораторной работы студенты должны повторить материал лекций, а так же изучить теоретический материал по теме лабораторной работы, изложенный в рекомендуемой учебной литературе по курсу, а также в приложении к работе.

Так, содержание лабораторных работ предполагает исследование общих принципов работы в MathCad и MatLab, моделирование линейных систем и спектральный анализ сигналов. Студентам необходимо в процессе самостоятельной домашней работы составить отчет и ответить на контрольные вопросы по допуску к лабораторной работе.

Защита лабораторных работ может проводиться как в индивидуальной устной форме, так и в форме тестирования.

Вопросы для защиты представлены в содержании каждой лабораторной работы. По результатам защиты лабораторной работы выставляется зачет.

На проведение лабораторных работ программой отводится 10 часов. Количество часов на выполнение каждой работы, а также её тема, указаны в таблице 1.

 

Таблица 1 - Перечень лабораторных работ

Перечень лабораторных работ	Кол-во часов
Общие принципы работы системы MatLab
Моделирование линейных систем
Генерация сигналов в MatLab
Спектральный анализ сигналов
Итого:

Лабораторная работа 1

Лабораторная работа 2

Порядок выполнения

6.1 Создать модель фильтра (п. 4.2.1) в программе Simulink.

Подготовить и ввести в программу исходные данные (п. 4.2.2) в соответствии с заданным вариантом (по номеру компьютера), необходимые для синтеза аналогового ФНЧ: аппроксимация – по Баттерворту; частота среза Fс; коэффициент усиления K0;

порядок фильтра N=2.

Вариант
Fс	100 Гц	200 Гц	300 Гц	400 Гц	500 Гц	600 Гц
K0

ФНЧ Баттерворта второго порядка определяется следующим образом:

, где B0=K0, A0=1, , .

6.2 Подать на вход ФНЧ единичное ступенчатое воздействие (п. 4.2.4). Вычислить переходную характеристику системы h1(t). Построить графики входного ступенчатого воздействия и переходной характеристики на экране осциллографа Scope (п. 4.2.5).

6.3 Определить время установления tуст выходного сигнала на уровне 95 % (или 105 % при наличии колебательного переходного процесса). Сравнить полученный график и значение tуст с данными, полученными при моделировании системы в программе Mathcad.

6.4 Выбрать в качестве входного гармонический сигнал X(t) с частотой Fx равной частоте среза фильтра Fc и единичной амплитудой (п. 4.2.3). Построить графики входного X(t) и выходного сигнала Y(t) (п. 4.2.5).

Повторить п.6.3 для гармонического сигнала с частотой Fx=2×Fc.

 

7 Содержание отчета:

7.1 Название и цель работы

7.2 Листинг выполненных программ согласно пункту 5 с описание команд

7.4 Выводы по полученным результатам

7.3 Ответы на контрольные вопросы

8 Контрольные вопросы:

8.1 Свойства d-импульса и прямоугольного ступенчатого сигнала.

8.2 Что такое импульсная и переходная характеристика системы. Взаимосвязь импульсной и переходной характеристик.

8.3 Что такое передаточная функция и частотная системы.

8.4 Взаимосвязь импульсной характеристики и передаточной функции системы.

8.5 Как определяются время установления системы и частоты среза АЧХ.

8.6 Указать где и в каком порядке должны быть введены значения в блоке параметров фильтра Transfer Fcn, если передаточная функция

.

8.7 Каким образом можно одновременно проанализировать три сигнала с разных источников.

8.8 Как задать интервал времени моделирования в программе Simulink.

8.9 Какие блоки программы Simulink используются для создания гармонических сигналов, ступенчатых воздействий, прямоугольных и треугольных импульсов.

Лабораторная работа 3

Генерация сигналов в MatLab

1 Цель работы:

1.1 Изучение средств системы по генерации сигналов, разложению их в ряд Фурье и дискретному преобразованию Фурье, приобретение практических навыков их использования

 

2 Литература:

2.1 Оппенгейм А., Шафер Р. Цифровая обработка сигналов. Издание 3-е, исправленное. — Москва: Техносфера 2012 г.— 1048 с.

2.2 Умняшкин С. В. Теоретические основы цифровой обработки и представления сигналов: Учебное пособие. — Москва: Техносфера 2012 г.— 368 с. — Электронное издание.

2.3 Солонина А.И., Клионский Д.М., Меркучева Т.В., Перов С.Н. Цифровая обработка сигналов и MATLAB. — Санкт-Петербург: БХВ-Петербург 2013 г.— 512 с.

2.4 Солонина А.И. Цифровая обработка сигналов. Моделирование в Simulink. — Санкт-Петербург: БХВ-Петербург 2012 г.— 432 с. — Электронное издание.

 

3 Основное оборудование:

3.2. Персональный компьютер.

4 Подготовка к работе:

Сигнал может быть:

Аналоговый – исходный физический сигнал, являющийся непрерывной функцией времени;

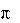
Дискретный – результат преобразования аналогового сигнала в последовательность чисел, которые являются значениями сигнала в отдельные (дискретные) моменты времени, называются отсчетами. Как правило, отсчеты берутся через равные промежутки времени т, называемые периодом дискретизации. Величина, обратная периоду дискретизации, называется частотой дискретизации: fd = 1/t. Круговая частота определяется, как d = 2 /t;

Цифровой; в вычислительных устройствах отсчеты сигнала представляются в виде двоичных чисел. Процесс преобразования отсчетов в числа называется квантованием по уровню, а возникшие при этом ошибки – ошибками

или шумами квантования. Сигнал, дискретный во времени и квантованный по уровню, называют цифровым.

 

Для того, чтобы гармонический сигнал мог быть адекватно представлен дискретными отсчетами, его частота не должна превышать половины частоты дискретизации: fN = fD/2. Эта частота называется частотой Найквиста.

Дискретный сигнал представляет собой последовательность чисел,

поэтому для его расчета формируют вектор опорных значений времени. Для этого удобно задавать значение частоты дискретизации Fs и использовать обратную величину частоты дискретизации в качестве шага временного ряда.

 

Пример 1. Сформировать затухающий гармонический сигнал:

>> Fs = 8e3; % частота дискретизации 8 кГц

>> t = 0:1/Fs:1; % одна секунда дискретных значений времени

>> A = 2; % амплитуда – два вольта

>> f0 = 1e3; % частота гармонического сигнала 1кГц

>> phi = pi/4; % начальная фаза гармонического сигнала – 45˚

>> s1 = A*cos(2*pi*f0*t+phi); % гармонический сигнал

>> alpha = 1e3; % скорость затухания

>> s2 = exp(–alpha*t).*s1; % затухающая синусоида

% вывод (визуализация) затухающей синусоиды различными способами

>> figure,subplot(2,2,1);plot(s2(1:100))

>> subplot(2,2,2);plot(s2(1:100),'.')

>> subplot(2,2,3);stem(s2(1:100))

>> subplot(2,2,4);stairs(s2(1:100))

 

Функции генерации дискретных сигналов

Функции генерации одиночных импульсов

В пакете Signal Processing системы MatLab имеются функции, генерирующие часто встречаемые на практике непериодические сигналы:

 

rectpuls – прямоугольный импульс вида

 

rect(t)

1, t 1

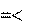2;

0, t

 

sinc– импульс вида sin c(t)

sin(t);

t , t   0,   t .

t

 

tripuls – треугольный импульс вида

(t)

 

Прямоугольный импульс

Синтаксис

y = rectpuls(t,width),

где t – вектор значений времени;, width – ширина (длительность) импульса (по умолчанию width = 1, в этом случае функция rectpuls производит результат, соответствующий математической функции rect).

 

Пример 2. Сформировать прямоугольный импульс:

>> t = –0.6:0.01:1;

>> y = rectpuls(t);

>> figure,plot(t,y);

>> ylim([0 1.5])

 

Пример 3. Сформировать пару разнополярных прямоугольных импульсов с амплитудой 5 В и длительностью 20 мс, расположенных справа и слева от начала отсчета времени:

>> fs = 1e3;

>> t = –40e–3:1/Fs:40e–3;

>> T = 20e–3;

>> A = 5;

>> s = –A*rectpuls(t+T/2,T) = A*rectpuls(t–T/2,T);

>> figure,plot(t,s)

>> ylim([–6 6])

Функция Дирака

Наибольший интерес в теоретическом отношении представляет предельный случай прямоугольного импульса, когда его длительность стремится к нулю, а высота импульса стремится к бесконечности. В этом случае в результате предельного перехода получаем новую функцию с необычайными свойствами. Она называется «дельта-функция», или функция Дирака. Эта функция обладает следующими свойствами:

1) Она равна нулю при t < 0 и t > 0 и бесконечна в точке t = 0:

(t) 0, t 0;

, t 0

 

(t)dt 1

2).

 

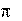Импульс с ограниченной полосой частот

Для формирования импульса вида sin(

Синтаксис y = sinc(t),

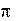где t – вектор значений времени.

t) /)

t используется функция sinc:

 

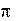Пример 4. Сформировать импульс вида sin(

>> f = –10:0.1:10;

>> y = sinc(f);

>> figure,plot(f,y);

>> ylim([–2 2])

t) /(

t):

 

Треугольный импульс

Для формирования треугольного импульса с единичной амплитудой служит функция tripuls:

Синтаксис

y = tripuls(t,width,skew),

где t – вектор значений времени; width – ширина (width = 1 по умолчанию) импульса; skew – коэффициент асимметрии импульса, определяющий положение его вершины.

Пик импульса расположен при t = width*skew/2, параметр skew должен лежать в диапазоне от –1 до 1 (skew = 0 по умолчанию).

 

Пример 5. Сформировать симметричный трапециевидный импульс с амплитудой 10 В и размерами верхнего и нижнего оснований 20 и 60 мс соответственно. Частота дискретизации 1кГц:

>> Fs = 1e3;

>> t = –50e–3:1/Fs:50e–3;

>> A = 10;

>> T1 = 20e–3;

>> T2 = 60e–3;

>> s = A*(T2*tripuls(t,T2)–T1*tripuls(t,T1))/(T2–T1);

>> figure,plot(t,s)

 

Функции генерации последовательности импульсов

Функция формирования конечной последовательности импульсов pulstran

Для генерации конечной последовательности импульсов одинаковой формы с произвольно задаваемыми задержками и уровнями служит функция pulstran.

Синтаксис

y = pulstran(t, d, ‘func’, p1, p2, …) y = pulstran(t, d, p, fs, 'method')

Сами импульсы могут задаваться одним из двух способов:

1) Именем функции, генерирующей импульс;

2) Рассчитанным вектором отсчетов, с помощью которого задается форма импульса.

 

Для первого способа функция вызывается следующим образом: y = pulstran(t, d, ‘func’, p1, p2, …),

где t – вектор значений времени; d – вектор задержек (если d – двухстолбцовая матрица, то первый столбец трактуется как задержки импульсов, а второй – как их уровни); ‘func’ – имя функции, генерирующей одиночный импульс; оставшиеся параметры – p1, p2, … – дополнительные.

 

Пример 6. Сформировать пять симметричных треугольных импульсов, интервалы между которыми линейно увеличиваются, а амплитуды экспоненциально уменьшаются:

>> Fs = 1e3; % частота дискретизации

>> t = 0:1/Fs:0.5; % дискретное время

>> tau = 20e–3; % длительность импульса

>> d = [20 80 160 260 380]'*1e–3; % задержки импульсов

>> d(:,2) = 0.8.^(0:4)'; % амплитуды импульсов

>> y = pulstran(t,d,'tripuls',tau);

>> figure,plot(t,y);

Для второго способа надо рассчитать вектор отсчетов импульса и вызвать функцию следующим образом:

y = pulstran(t, d, p, fs, 'method').

Смысл входных параметров t и d тот же, что и раньше. Вектор р должен содержать отсчеты одиночного импульса, а параметр fs указывает частоту дискретизации, использованную при расчете этого вектора. Считается, что первый отсчет из вектора р соответствует нулевому моменту времени. Так как частота fs может не совпадать с шагом значений вектора t, и задержки из вектора d тоже не обязательно кратны этому шагу, для пересчета задержанных импульсов к сетке моментов времени t в общем случае надо задавать интерполяцию. Метод интерполяции задается в параметре 'method'. Он может принимать следующие значения: 'nearest', 'linear', 'cubic', 'v5cubic', 'spine', 'chip'. По умолчанию fs= 1 и 'method' = 'linear'.

 

Пример 7. Сформировать последовательность из 6 импульсов, имеющих форму одного периода функции sin(t)2. Длительность импульсов равна 60 мс, частота его дискретизации составляет 400 Гц. Расстояние между центрами

импульсов будет равным 64 мс, а частота дискретизации выходного сигнала составляет 1 кГц. Импульсы будут затухать с ростом номера.

>> % Генерация вектора отсчетов одиночного импульса

>> Fs0 = 400; %частота дискретизации импульсов

>> tau = 60e–3; % длительность импульсов

>> t0 = 0:1/Fs0:tau; % дискретное время для импульса

>> s0 = sin(pi*t0/tau).^2; % вектор отсчетов импульса

>> % Генерация последовательности импульсов

>> Fs = 1e3;

>> t = 0:1/Fs:0.5;

>> d = (1:6)'*64e–3;

>> d(:,2) = 0.6.^(0:5)'

>> y = pulstran(t,d,s0,Fs0);

>> figure,plot(t,y)

 

Функция формования последовательности прямоугольных импульсов square

Для генерации последовательности прямоугольных импульсов служит функция square:

Синтаксис

y = square(t,duty),

где t – вектор значений времени; duty – коэффициент заполнения – величина, обратная скважности (в процентах), т. е. отношение длительности импульса к периоду. По умолчанию duty = 50, т. е. генерируется меандр.

 

Пример 8. Сформировать однополярные прямоугольные импульсы с амплитудой 3 В, частотой следования 50 Гц и длительностью 5 мс.

>> Fs = 1e3; % частота дискретизации

>> t = –10e–3:1/Fs:50e–3; % дискретное время

>> A = 3; % амплитуда

>> f0 = 50; % частота следования импульсов

>> tau = 5e–3; % длительность импульсов

>> s = (square(2*pi*t*f0,f0*tau*100)+1)*A/2;

>> figure,plot(t,s);

>> ylim([0 5])

 

Ряд Фурье

Разложению в ряд Фурье могут подвергаться периодические сигналы. При этом они представляются в виде суммы гармонических функций либо комплексных экспонент с частотами, образующими арифметическую прогрессию. Для того, чтобы такое разложение существовало, фрагмент сигнала длительностью в один период должен удовлетворять условиям Дирихле:

1. Не должно быть разрывов второго рода (с уходящими в бесконечность ветвями функции);

2. Число разрывов первого рода (скачков) должно быть конечным;

3. Число экстремумов должно быть конечным.

 

Существует несколько форм представления: синусно-косинусная, вещественная, комплексная.

Представим синусно-косинусную форму ряда Фурье:

 

s(t)

(akcos(k

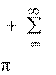
k 1

1t)

bk sin(k

1t)), (1)

где 1

2 / T

– круговая частота, кратные ей частоты k

1 называются

гармониками.

Коэффициенты ряда ak

 

и bk

 

рассчитываются по формулам (2), (3):

ak 2 T

bk 2 T

T / 2

s(t) cos(k

T / 2

T / 2

s(t) sin(k

T / 2

1t)dt; (2)

1t)dt. (3)

Слагаемое с константой a 0

представляет собой среднее сигнала на

периоде, рассчитываемое по формуле (4):

a0 1

2 T

T / 2

s(t)dt. (4)

T / 2

Если s(t) является четной функцией, то все bkбудут равны нулю, и в фор- муле ряда Фурье будут присутствовать только косинусные слагаемые; если s(t) является нечетной функцией, то останутся только синусные слагаемые.

Совокупность амплитуд гармоник ряда Фурье называется амплитудным спектром, а совокупность их фаз – фазовым спектром.

Разложение в ряд Фурье последовательности прямоугольных импульсов

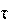Рассмотрим последовательность прямоугольных импульсов с амплитудой А, длительностью и периодом повторения T. Начало отсчета времени возьмем расположенным в середине импульса. Данный сигнал является четной функцией, и при разложении его в ряд Фурье будут присутствовать только

косинусные слагаемые

ak, равные

ak 2

/ 2 A cos(2 k t)dt

2A sin(2).

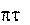
T / 2 T k T

Отношение периода к длительности импульсов называется скважностью

последовательности импульсов q

T /. Если ввести этот параметр в формулу

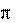для коэффициента ряда Фурье, а затем привести формулу к виду получим:

sin(x) / x,

ak 2A sin(k)

sin(k) 2A q

.

k q q k

q

Поскольку при x

sin(x) / x

1, то a0

2

AA

.

q T

Само представление последовательности прямоугольных импульсов в виде ряда Фурье можно записать в виде формулы:

s(t) A

2A sin(k) cos(2 k t).

q k1 k q T

Последовательность прямоугольных импульсов со скважностью, равной двум, когда длительность импульсов и промежутки между ними равны, называется меандром. Представление меандра в виде ряда Фурье может быть записано следующим образом:

s(t)

A2A (cos(2)

1 cos(3 2)

1 cos(5 2)

...).

t

t

t

2 T 3 T 5 T

 

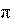
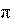
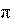
Пример 9. Получить меандр сложением отдельных гармоник:

>> N = 8; % чиcло ненулевых гармоник

>> t = –1:0.01:1; % вектор моментов времени

>> A = 1; % амплитуда

>> T = 1; % период

>> nh = (1:N)*2–1; % номера ненулевых гармоник

>> harmonics = cos(2*pi*nh'*t/T); % строки-гармоники

>> Am = 2/pi./nh; % амплитуды гармоник

>> Am(2:2:end) = –Am(2:2:end); % чередование знаков

>> s1 = harmonics.*repmat(Am',1,length(t));

>> s2 = cumsum(s1); % частичные суммы гармоник (суммирование с накоплением)

>> for k = 1:N

>> subplot(4,2,k)

>> plot(t,s2(k,:))

>> end;

Так как последовательность прямоугольных импульсов содержит скачки (разрывы 1-го рода), в окрестностях точек разрывов суммирование ряда Фурье дает наклонный участок, а на примыкающих к разрыву участках сумма ряда Фурье дает заметные пульсации. Это явление, присущее рядам Фурье для любых сигналов с разрывами 1-го рода, называется эффектом Гиббса.

Прямое и обратное преобразование Фурье

Преобразование Фурье является инструментом спектрального анализа непериодических сигналов. В системе MatLab для вычисления прямого преобразования Фурье одномерных сигналов используется функция fft:

Синтаксис

y = fft(x) – вычисляет прямое ДПФ (дискретное преобразование Фурье) для вектора х; если х – матрица, преобразование производится для каждого ее столбца по отдельности;

y = fft(x,N) – вычисляет прямое ДПФ; перед вычислением предварительно приводит исходные данные к размеру N, урезая их или дополняя нулями.

Для вычисления обратного преобразования Фурье одномерных сигналов используется функция ifft:

Синтаксис

x = ifft(y,N) – вычисляет обратное ДПФ; предварительно приводит исходные данные к размеру N, урезая их или дополняя нулями.

Для вычисления прямого ДПФ двумерного сигнала используется функция

fft2, обратного ДПФ – ifft:

Синтаксис

y = fft2(x,N) – вычисляет прямое ДПФ для матрицы х;

y = fft2(x,N) – вычисляет прямое ДПФ; перед вычислением предварительно приводит исходные данные к размеру N, урезая их или дополняя нулями.

x = ifft2(y) – вычисляет обратное ДПФ для матрицы y;

x = ifft2(y,N) – вычисляет обратное ДПФ; перед вычислением предварительно приводит исходные данные к размеру N, урезая их или дополняя нулями.

При выводе спектральных графиков иногда желательно, чтобы компонента с нулевой частотой вектора х находилась в центре, а диапазон отображаемых частот простирался от –fD/ 2 до fD/ 2. Сделать это позволяет функция fftshift, которая меняет местами половины переданного ей вектора.

Синтаксис

y = fftshift(x)

В рассчитанном преобразовании Фурье присутствуют наряду с вещественными коэффициентами и мнимые. Поэтому для визуализации ДПФ необходимо определить модуль ДПФ. Для этого и используют функцию abs – определение модуля аргумента.

Синтаксис

у = abs(х)

Для оценки энергии на различных частотах применяется спектральная плотность мощности (СПМ), равная произведению вектора ДПФ на сопряженный ему вектор. Для вычисления сопряженного вектора используется функция conj.

Синтаксис

у = conj(х)

Поскольку преобразования Фурье переводит сигнал из временной области в частотную, для вывода графика спектра надо задать вектор нормализованных частот. Размер этого вектора должен совпадать с размером вектора ДПФ (размер вектора вычисляет функция size).

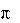Ниже приведены примеры формирования прямоугольных импульсов и импульса вида sin(t) / (t) и их спектров и СПМ.

 

Пример 10. Сформировать спектр и СПМ прямоугольного сигнала:

>> Fs = 8e3;

>> t = –40e–3:1/Fs:40e–3;

>> T = 20e–3;

>> s = rectpuls(t,T);

>> figure,plot(t,s)

>> ylim([–2 2])

>> Fs = fft(s);

>> Pfs = Fs.*conj(Fs);

>> f = 1000/256*(1:max(size(Fs))); % вектор нормализованных частот

>> F = fftshift(Pfs);

>> figure,plot(f,F),grid % СПМ

>> xlim([1150 1350]);

>> F = fftshift(abs(Fs));

>> figure,plot(f,F),grid % преобразование Фурье

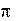>> xlim([1000 1500]);

 

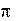Пример 11. Cформировать спектр и СПМ импульса вида sin(

>> t = –4:0.1:4;

>> y = sinc(t);

>> figure,plot(t,y);

>> F = fft(y);

>> f = 1000/256*(1:max(size(F)));

>> F1 = fftshift(abs(F));

>> figure,plot(f,F1); % преобразование Фурье

>> F1 = fftshift(F.*conj(F));

>> figure,plot(f,F1); % СПМ

t) /(

t).

 

Пример 12. Использовать двумерное преобразование Фурье для сигнала

вида z

2 (x) *

2 (y)

>> t = –1:0.05:1;

>> y = tripuls(t);

>> plot(t,y)

>> [X,Y] = meshgrid(t);

>> Z1 = tripuls(X);

>> Z2 = tripuls(Y);

>> Z3 = Z1.*Z2;

>> figure,mesh(X,Y,Z3);

>> F = fft2(Z3);

>> Fa = fftshift(abs(F));

>> f1 = 1000*(1:max(size(F)))/526;

>> [f1,f2] = meshgrid(f1);

>> figure,mesh(f1,f2,Fa).

Преобразование Фурье часто используется для выделения основных частот сигнала, зашумленного помехами.

Пример 13. Сформировать сигнал, являющийся суммой двух синусоид с частотами 50 и 130 Гц и случайной компоненты с нулевым средним и с помощью ДПФ определить, какие частоты присутствуют в анализируемом сигнале.

>> t = 0:0.001:0.25; % задание вектора времени

>> x = sin(2*pi*50*t)+0.5*sin(2*pi*130*t) % задание сигнала

>> y = x+randn(size(t));

>> figure,plot(t,y);

Полученная зависимость не позволяет определить основные частоты сигнала. Для их определения рассчитаем и построим график СПМ, используя ДПФ сигнала:

>> Y = fft(y);

>> Pyy = Y.*conj(Y);

>> f = 1000/256*(0:127);

>> figure,plot(f(1:50),Pyy(1:50))

>> title('Power spectral density')

>> xlabel('Frequency(Hz)')

5 Задание:

5.1 Сформировать затухающий гармонический сигнал Asin(2 ft +

+ с частотой дискретизации 5 кГц, вектор отсчетов времени задать от –1 до 1 с шагом, равным обратной величине частоты дискретизации, амплитуда равна 4 В, частота гармонического сигнала 1,5 кГц, начальная фаза гармонического сигнала 30 градусов, скорость затухания 100. Выдать на одном графике в разных подобластях два графика, используя функцию plot (красным цветом, точечной линией) и функцию stem (зеленым цветом, линия оканчивается символом ^).

5.2 Сформировать последовательности из 4 импульсов, имеющих форму одного периода функции cos(t)2. Длительность импульсов равна 70 мс, частота его дискретизации 250 Гц. Расстояние между центрами импульсов будет равным 70 мс, а частота дискретизации выходного сигнала 1 кГц. Вектор отсчетов времени задать от –0 до 0.5 с шагом, равным обратной величине частоты дискретизации. Импульсы затухают с ростом номера.

5.3 Сформировать меандр сложением отдельных 16 гармоник, процесс получения отобразить в 4 столбцах (столбец из 4 строк).

5.4 Сформировать меандр соответствующей функции и вывести его график.

5.5 Сформировать одиночный прямоугольный импульс и его Фурье-образ. Частота дискретизации равна 1е3, вектор отсчетов времени задать от –0 до 40е– 3 с шагом, равным обратной величине частоты дискретизации, амплитуда равна 5 В, длительность импульса равна 20е–3. Выдать график прямоугольного импульса, (отлимитировать значения по оси у от –6 до 6 командой ylim([–6 6]), задаваемой после команды plot). Вывести сетку. Значения частоты для вывода Фурье преобразования задать f = 1 000 · (1: 41) / 512. Спектральный график вывести с нулевой частотой, находящейся в центре, для чего использовать соответствующую функцию.

5.6 Сформировать одиночный сигнал вида sin(x)/x и его СПМ. Вектор времени задать от –5 до 5 с шагом, равным 0.01. Значения частоты для вывода СПМ задать равными f = 1 000 · (1: 1001) / 512. Спектральный график вывести с нулевой частотой, находящейся в центре, для чего использовать соответствующую функцию. Полученный график отлимитировать от 900 до 1 000.

5.7 Построить графики трехмерных функций и их Фурье-преобразований:

а) Z1 = rect(x)*rect(y);

б) Z2 = sinc(x)*sinc(y),

используя результаты выполнения заданий 5 и 6 соответственно.

6 Содержание отчета:

6.1 Название и цель работы

6.2 Листинг выполненных программ согласно пункту 5 с описание команд и полученными графиками

6.3 Ответы на контрольные вопросы

7 Контрольные вопросы:

7.1 В чем заключается эффект Гиббса?

7.2 Какие функции MatLab используются для генерации одиночных импульсов?

7.3 Какие существуют способы задания импульсов для функции pulstran?

7.4 Какие функции вычисляют ДПФ в MatLab?

7.5 Какие дополнительные функции используются для того, чтобы получить график преобразования Фурье и спектральную плотность мощности?

7.6 Для чего применяют БПФ к зашумленному сигналу?

Лабораторная работа 4

Создание модели фильтра

Для проведения спектрального анализа аналогового фильтра требуется составить следующую структурную схему (модель), рис. 5.

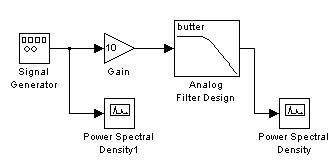
Рис. 5. Структурная схема для проведения спектрального анализа фильтра

 

Модель аналогового фильтра (в данной работе исследуется фильтр Баттерворта) выглядит так, как показано на рис. 6, и создается с помощью следующих блоков:

· аналоговый фильтр с единичным усилением Analog Filter Design

(DSP blockset/Filtering/Filter Design/Analog Filter Design), рис. 7;

· усилитель Gain (Simulink/Math/Gain), рис. 8.

Рис. 6. Модель фильтра Баттерворта в программе MATLAB

Рис. 7. Расположение блока Analog Filter Design

Рис. 8. Расположение блока усилителя Gain

 

Исходные данные необходимые для синтеза аналогового фильтра:

· вид аппроксимации;

· порядок фильтра N;

· пульсации в полосе пропускания / заграждения (не требуется для фильтров Баттерворта);

· коэффициент усиления K.

Исходные данные задаются в блоке параметров фильтра Block Parameters: Analog Filter Design ( рис. 9), где:

· Design method – вид аппроксимации;

· Filter order – порядок фильтра.

Коэффициент усиления задается отдельно в блоке параметров усилителя Block Parameters: Gain (рис. 10).

Рис. 9. Блок параметров Analog Filter Design

 

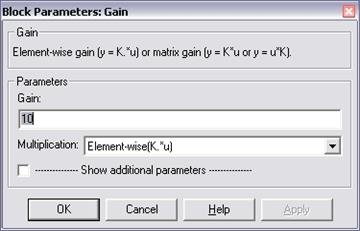
Рис. 10. Окно настройки параметров блока Gain

 

2.2.2. Блок Power Spectral Density (анализатор спектра)

Для просмотра спектральной плотности сигнала используют анализаторы спектра Power Spectral Density (Simulink Extras/Additional Sinks/Power Spectral Density), рис.11.

а) б)

Рис. 11. Расположение блока Power Spectral Density (а) и результаты анализа спектра (б)

 

В окне настройки Block Parameters: Power Spectral Density, рис. 12, задаются следующие параметры анализатора спектра:

· Length of buffer – длина буфера (по умолчанию 128);

· Number of points for fft – число анализируемых точек (по умолчанию 512);

· Plot after how many points– количествоточек, после которого производится построение графика (по умолчанию 64);

· Sample time – период дискретизации.

Все параметры, кроме периода дискретизации, должны быть кратны 2^N, где N – целое число.

 

Рис. 12. Окно настройки параметров блока Power Spectral Density

Результаты анализа спектра, выполняемого блоком Power Spectral Density, представляются втрех окнах (рис. 11.б):

· исследуемый сигнал (Time history);

· амплитудный спектр (Power Spectral Density);

· фазовый спектр (Power Spectral Density (phase)).

Чтобы просмотреть спектр сигнала нужно запустить работу модели. Это можно сделать, вызвав меню Simulation инажав команду Start, либо нажав сочетание клавиш Ctrl + T или же щелкнув пиктограмму – Start simulation.