РГР-2 – «Метрические задачи»

 

РГР-2 выполняется на миллиметровой бумаге форматов А4 и А3 в карандаше. Исходными данными для выполнения РГР-2 являются результаты решения РГР-1 или берунся из прил. 2.

Состав задания. По расчетной схеме (результаты решения РГР № 1) определить основные геометрические характеристики корпуса, штока, иглы и поводка регулятора. Т.е. решить следующие задачи.

1. Способом прямоугольного треугольника определить углы наклонов и натуральные величины отрезков [ED] и [EN](угол наклона ε° отрезка [ED] к плоскости π₂и угол наклона η° отрезка [EN] к плоскости π₁). Угол ε° определяется для нечетных вариантов, а угол η° - для четных.

2. Используя расчетную схему, построить проекции пирамиды SABC и ее высоты SE на плоскостях π₁и π₂. Определить видимость ее элементов, пользуясь способом конкурирующих точек.

3. Способом вращения определить натуральную величину удаления точки S от плоскости заданной треугольником ∆ABC и натуральную величину треугольника ∆ABC.

4. Способом замены плоскостей проекций определить кратчайшее расстояние между ребром [AS] и стороной [ВС], а также угол наклона этой стороны к плоскости π₁, т.е. а°.

5. Способом замены плоскостей проекций определить угол φ° между гранями ACS и BCS.

6. Способом замены плоскостей проекций определить угол δ° между ребром [AS]и гранью SBC.

Порядок выполнения работы.

1. Способом прямоугольного треугольника определить углы наклонов и натуральные величины отрезков [ED] и [EN] (угол наклона ε° отрезка [ED] к плоскости π₂и угол наклона η° отрезка [EN] к плоскости π₁).

Сущность (рис. 9) данного способа сводится к тому, что длина отрезка прямой равна гипотенузе прямоугольного треугольника. В этом треугольнике один катет есть проекция отрезка, а второй катет равен алгебраической разности расстояний концов отрезка до той же плоскости проекции, на которой взят первый катет.

Рис. 9

Примечание. Натуральная величина угла наклона отрезка к плоскости проекции определяется при построении натуральной величины отрезка на этой плоскости проекций.

2. Используя расчетную схему (результат решения РГР-1), построить проекции пирамиды SABC и ее высоты SE на плоскостях π₁ и π₂. Определить видимость ее элементов, пользуясь способом конкурирующих точек. Пример построения показан на рис. 10.

Рис. 10

3. Способом вращения определить натуральную величину удаления точки S от плоскости заданной треугольником ∆ABC и натуральную величину треугольника ∆ABC.

Задача решается двумя вращениями. При первом вращении определяется расстояние от точки S до плоскости заданной треугольником ∆ АВС, а при втором вращении – натуральная величина треугольника ∆ АВС.

Рассмотрим пример решения этой задачи (рис. 11).

Первое вращение. При первом вращении необходимо повернуть треугольник ∆ АВС и точку S вокруг оси, перпендикулярной к плоскости проекций, так, чтобы плоскость ∆ АВС стала проецирующей, т.е. перпендикулярной к плоскости проекций. Тогда перпендикуляр от проекции точки S до вырожденной проекции плоскости будет являться искомой величиной.

На рис. 15 задан треугольник AВС, плоскость которого занимает общее положение. Требуется повернуть треугольник вокруг оси, перпендикулярной к плоскости проекций, так, чтобы его плоскость стала, например, фронтально-проецирующей. Для этого в начале проведем в треугольнике горизонталь [ А1 ]. Затем повернем горизонталь [ А1 ] вместе с треугольником ∆ АВС и точкой S вокруг оси i до ее проецирующего положения. Здесь ось вращения i проходит через точку А и перпендикулярна плоскости π₁.

При построении необходимо учитывать следствие: если вращать геометрический образ вокруг оси, перпендикулярной к плоскости проекции, то проекция на эту плоскость не изменяется ни по виду, ни по величине – меняется лишь положение этой проекции.

В нашем случае на π ₁ Δ A ₁ B ₁ C ₁ = Δ A ⁰₁ B ⁰₁ C ⁰₁, а положение точки S ₁ относительно Δ A ₁ B ₁ C ₁ точно такое же, как S ⁰₁ относительно Δ A ⁰₁ B ⁰₁ C ⁰₁.

Что же касается другой проекции (на плоскости π ₂), то все ее точки перемещаются по прямым, параллельным оси проекций. Исключение составляют проекции точек, которые располагаются на оси вращения (они остаются на месте). Следовательно, эта проекция изменяется по форме и по величине.

После такого построения проекция треугольника ABC на плоскости π₂ вырождается в проецирующую плоскость, а перпендикуляр из точки S ₂⁰ до вырожденной проекции треугольника ∆ А ₂⁰ В ₂⁰ С ₂⁰ и есть удаления точки S от плоскости заданной треугольником ∆ABC.

Второе вращение. При втором вращении плоскость треугольника ∆ А ⁰ В ⁰ С ⁰ переводится в плоскость уровня. Для этого его поворачивают вокруг оси j перпендикулярной плоскости π ₂ и проходящей через точку С. Т.е. вырожденную проекцию треугольника поворачивают до положения параллельного оси ОХ: ∆ А ₂⁰ В ₂⁰ С ₂⁰ → ∆ А ₂¹ В ₂¹ С ₂¹ ∥ ОХ. При этом новая проекция треугольника ∆ А ₁¹ В ₁¹ С ₁¹ будет натуральной величиной треугольника ∆ABC.

4. Способом замены плоскостей проекций определить кратчайшее расстояние между ребром [AS] и стороной [ВС], а также угол наклона этой стороны к плоскости π₁, т.е. а°.

В нашем случае расстояние между ребром [ AS ] и стороной [ ВС ] можно рассматривать как расстояние между двумя скрещивающимися прямыми, которое определяется отрезком перпендикуляра, общего для этих прямых.

Определение натуральной величины перпендикуляра между двумя скрещивающимися прямыми достигается путем двух замен плоскостей проекций (рис. 12).

 

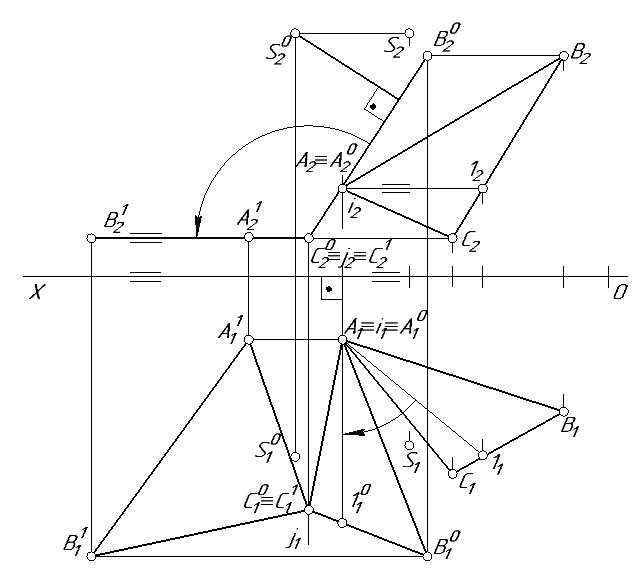
Рис.11

Первая замена. Выбираем новую плоскость проекций π₄, параллельную отрезку [ ВС ] и перпендикулярную плоскостиπ₁.

Примечание. Так как в задании требуется определить еще и угол наклона прямой [ ВС ] к плоскости π₁,то замену плоскостей проекций произ­водим относительно прямой [ ВС ].

Проводим ось x ₁ параллельно B ₁ C ₁. Построим в новой системе π₁/ π₄проекции прямых [ ВС ]и[ SA ]. Проекция [ В ₄ С ₄] есть натуральная величина отрезка [ ВС ], а угол наклона ее к оси (α⁰) является углом наклона прямой [ ВС ] к плоскости проекцийπ₁.

Вторая замена. Новую плоскость проекций π₅ выбираем перпендикулярно [ ВС ] и плоскости п ₄. Проводим ось x₂ перпендикулярно [ В ₄ С ₄] и строим в новой системе π₄/π₅ проекции прямых [ ВС ]и[ SA ].

В результате построения прямая [ ВС ] выродится в точку (в проецирующую прямую). Следовательно, перпендикуляр от этой точки до проекции [ S ₅ A ₅] есть натуральная величина кратчайшего расстояния между [ ВС ] и[ SA ].

 

Рис. 12

5. Способом замены плоскостей проекций определить угол φ⁰ между гранями ACS и BCS.

Общая сторона [ SC ] треугольников ASC и BCS является ребром двугранного угла. Плоскость, перпендикулярная к ребру двугранного угла, параллельна сторонам линейного угла, которыми измеряется данный двугранный угол. Следовательно, на эту плоскость двугранный угол проецируется в натуральную величину.

Решение этой задачи проводится двумя заменами (рис. 13). При первой замене ребро [ SC ] переводится в прямую уровня, а при второй замене прямая уровня преобразуется в проецирующею прямую. При таком преобразовании плоскости граней станут проецирующими, а угол между вырожденными проекциями этих плоскостей и будет искомой величиной.

Первая замена. Вводим новую плоскость проекций π ₄ перпендикулярно π ₁ и параллельно ребру [ SC ]. Для этого проводим новую ось Х ₁параллельно горизонтальной проекции ребра [ C₁S₁ ] двугранного угла, образованного плоскостями треугольников ACS и BCS, и строим на плоскости π ₄ новые проекции A ₄ C ₄ S ₄и B ₄ C ₄ S ₄. На плоскости π₄ ребро [ CS ] проецируется в натуральную величину.

Вторая замена. Вводим новую плоскость проекций π ₅ перпендикулярно π ₄ и перпендикулярно ребру [ SC ]. Для этого проводим новую ось Х ₂ перпендикулярно к проекции C ₄ S ₄ и строим на плоскости π₅ проекции A ₅ C ₅ S ₅ и B ₅ C ₅ S ₅. На плоскость π₅ ребро [ CS ] проецируется в точку C ₅ ≡S ₅ (совпадают), а плоскости треугольников ACS и BCS – в прямые соответственно A ₅ C ₅ S ₅ и B ₅ C ₅ S ₅. Угол между этими прямыми равен двугранному углу φ °.

 

Рис.13

6. Способом замены плоскостей определить угол δ ° между ребром [ AS ] и гранью SBC, а также натуральную величину грани SBC.

Угол между заданной плоскостью и прямой проецируется в истинную величину на плоскость проекций, перпендикулярную к заданной плоскости и параллельную прямой (рис. 14).

Плоскость треугольника SBC и отрезок [ SA ] в системе π₁/π₂ занимают общее положение. Для решения поставленной задачи в плоскости треугольника проведем горизонталь или фронталь и последовательно сделаем три замены плоскостей проекций.

Первая замена. Новая плоскость проекций π₄ перпендикулярна плоскости треугольника SBC и плоскости π₁. Проводим ось х ₁ перпендикулярно С ₁ l ₁ и строим новые проекции геометрических образов на плоскости π₄. В результате такого построения плоскость треугольника SBC займет проецирующее положение.

 

Рис. 14

 

Вторая замена. Новая плоскость проекций π₅ параллельна плоскости треугольника SBC и перпендикулярна плоскости π₄. Проводим ось х ₂ параллельно S ₄ B ₄ C ₄ и строим новые проекции геометрических образов на плоскости π₅. Теперь на плоскости π₅треугольник SBC будет проецироваться в истинную величину.

Теперь любая плоскость, перпендикулярная плоскости π₅,будет перпендикулярна и плоскости треугольника SBC.

Третья замена. Проведем третью новую плоскость проекций π₆парал­лельно [ AS ] и перпендикулярно π₅, т.е. ось х ₃ будет параллельна [ A ₃ S ₅]. На плоскость π₆ искомый угол δ ° проецируется в истинную величину.

7. Указания по выбору хода решения и оформления задач РГР-2.

Каждая задача решается отдельно от других задач, т.е. совмещение решения задач не допускается.

При решении задач способом вращения перпендикулярность к плоскости проекций π₁ или π₂ оси вращения i, j выбирается в зависимости от удобств построения и наглядности изображений.

При решении задач способом замены плоскостей проекций новые оси проекций проводятся так, чтобы они желательно не пересекали ранее построенных проекций.

Номера новых осей и новых плоскостей проекций обозначаются по порядку решения задач, а именно x ₁ х ₂, х ₃ ,... иπ₄, π₅, π₆,...

После решения метрических задач проводится проверка правильности их решения и устраняются выявленные ошибки.

Производится обводка эпюра согласно требованиям к линиям, приведенным в табл. 2.

На поле чертежа в правом нижнем углу заносятся фамилия и инициалы студента, номер учебной группы, номер варианта, а номер задачи - над каждой задачей с левой стороны. Пример оформления РГР-2 приведен в прил. 12.

Таблица 2

Требования к линиям РГР-2

 

№ п/п	Линии в РГР	Тип и толщина линии, мм	Цвет линии
	Оси i-i,х,х1...	0,4	Черный
	Начальных условий видимые	0,8	Черный
	Начальных условий невидимые	Штриховая 0,4	Черный
	Натуральные Величины	0,8	Красный
5 ’	Дополнительные Построения	0,2	Черный
	Линии связей	0,2 (длина 5-7 мм)	Черный
	Точки A B,...	О 0,2 (диаметр 1-2мм)	Черный