Метод решения задач как способ стимулирования познавательной активности школьников

 

Из всех предложенных принципов — прием решения задач является более способствующим развитию познавательной активности. В нем сочетается как бы несколько приемов, в т. ч. частично-поисковый (качественные задачи). Метод эвристической беседы подходит для углубленного обучения, но требует хорошей подготовки учащихся и не всегда подходит для применения теории в практике. Задания на сравнение и систематизацию материала применимы только на заключительных уроках. Такой метод как экспериментальные работы учащихся требуют хорошую техническую и материальную базу, много времени для подготовки к уроку, он также не всегда применим. Логико–поисковые самостоятельные работы учащихся очень хорошо сочетается с методом решения задач, но также требует хорошей подготовки учащихся. Метод же решения задач применим почти на всех уроках, его можно легко связать с жизнью, он реализует основные цели изучения физики – развитие логического мышления и умение решать задачи, он подходит для учеников разного уровня развития, требует знание теории и развитого мышления, при хорошем подборе интересны детям. Этот метод легко охватывает всех учащихся, не требует материальной и технической базы, сочетается с такими методами активизации как метод эвристической беседы и метод самостоятельных работ.

Образовательное, политехническое и воспитательное значение задач в куре физики трудно переоценить. В большинстве школ решению физических задач уделяется значительное внимание. Тем не менее, многие учащиеся постоянно испытывают затруднения в решении задач. Это объясняется не только сложностью данного вида и методике решения задач, особенно по школьному курсу физике.

Сознавая важность задач для изучения физики, многие учителя действуют по принципу: чем больше задач, тем лучше. В большинстве случаев это приводит к прямо противоположенным результатам: создает перегрузку учащихся, порождает неверие в свои силы, отталкивает от предмета. Поэтому вопросы методики решения задач оп физике в средней школе приобретает особое значение. При этом должны быть в полной мере использованы достижения педагогики в области развивающего и проблемного обучения, формирования физических понятий, применения технических средств обучения, научно-исследовательских и творческих заданий и т.д.

Физической задачей в учебной практике обычно называют небольшую проблему, которая в общем случае решается с помощью. Логических умозаключений, математических действий и эксперимента на основе законов и методов физики. По существу, на занятиях по физике каждый вопрос, возникший в связи с изучением учебного материала, является для учащихся задачей. Активное целенаправленное мышление всегда есть решение задач в широком понимании этого слова. Решение физических задач — одно из важнейших средств развития мыслительных, творческих способностей учащихся. Часто на уроках проблемные ситуации создаются с помощью задач, а этим активизируется мыслительная деятельность учащихся. Это и есть главный признака задач, позволяющий отнести их к активизирующим средствам. При чем в обучении физики решение задач это самое важное средство активизации при закреплении материала.

Ценность задач определяется, прежде всего, той физической информацией, которую они содержат. Некоторое понятие об основном физическом методе исследования явлений — природы— эксперимента, основу которого составляют измерения и математические исследования функциональной зависимости между физическим величинами целесообразно дать учащимся с помощью экспериментальных задач. Задачи с историческим содержанием позволяют показать борьбу идей, возникновение перед учеными трудности и пути их преодоления.

Решение задач — важное средство политехнического обучения и профориентации учащихся. Задачи содержат важные сведения о многих отраслях современного производства, массовых профессиях, поисках и находках изобретателей. При подготовке к урокам желательно использовать пособия по решению задач и для профессионально-технических училищ.

Значительный интерес для связи физики с живой природой, особенно в сельской школе, представляют задачи с биофизическим содержанием.

Наряду с задачами производственного и научного содержания большего значение для связи обучения с жизнью имеют задачи о физических явлениях в быту. Они помогают видеть физику «вокруг нас», воспитывают у учащихся наблюдательность. Например: рассчитайте стоимость электроэнергии, которая потребляется вашей стиральной машиной, холодильником или телевизором за 3 ч работы.

В целях политехнического обучения задачи важны также как средство формирования ряда практических умений и навыков. В процессе решения задач учащиеся приобретают умения и навыки применять свои знания для анализа различных физических явлений в природе, технике и быту, выполнять чертежи, рисунки, графики, производить расчеты, пользоваться справочной литературой, приборами и инструментами при решении экспериментальных задач.

Решение задач — чуткий барометр, по которому учитель может постоянно следить за успехами и настроением учеников и эффективностью своей учебно-воспитательной работы.

Методика решения задачи зависит от многих условий: от ее содержания, подготовки учащихся, поставленных перед ними целей. Тем не менее, существует ряд общих для большинства задач положений, которые следует иметь в виду при решении этих задач.

Главное условие успешного решения задач — знание учащимися физических закономерностей, правильное понимание физических величин, а также способов и единиц их измерения. К обязательным условиям относится и математическая подготовка учеников. Затем на первый план выступает обучение, как некоторым общим, так и специальным приемам решения задач определенных типов. Идеальным было бы создание для них алгоритмов решения, те точных предписаний, предусматриваемых выполнение элементарных операций, безошибочно приводящих к искомому результату. Но этот способ можно использовать только для решения типовых задач. Так как многие задачи нерационально (иногда и невозможно) решать алгоритмическим путем. Для большинства физических задач можно указать лишь некоторые общие способы и правила подхода к решению. Задачи нужно решать в определенной системе в соответствии с логикой изучаемого материала при максимальном внимании к общим фундаментальным закономерностям и фактам. Без этого каждая задача будет восприниматься, как нечто новое и перенос умений решения одних задач на решения других будет затруднен, что не будет способствовать активизации деятельности учащихся. Однако усвоение готовых и общих положений еще недостаточно для успешного решения всего многообразия физических задач.

Решение задачи — это активный познавательный процесс, большую роль в котором играют наблюдения физических явлений и эксперимент. Наблюдения и эксперимент позволяют создать соответствующие образы и представления, уточнить условия задачи, получить недостающие данные, установить зависимость между величинами и т д. Той же цели служат рисунки, чертежи и графики.

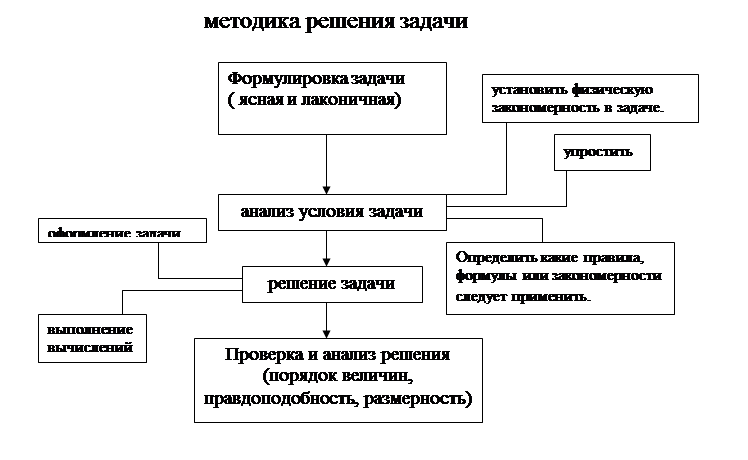
Решение задач как мыслительный процесс — это процесс анализа и синтеза. Формулировка задачи имеет большое значение. Она, как правило, должна быть ясной и лаконичной. Основные и существенные данные ее должны выступать на первый план, не заслоняясь побочными обстоятельствами.

Анализ условия задачи позволяет представить общую картину описанного в ней явления, при этом устанавливается, какие несущественны для рассматриваемой ситуации. Для того, чтобы познать явление, установить ту или иную физическую закономерность, необходимо его упростить, абстрагироваться от реальных условий, где явление никогда не существует в «чистом» виде. Например, в задачах по механике часто не учитывают трение, в задачах по механике часто не учитывают трение, в задачах по геометрической оптике — толщину «тонких» линз и т д. Одни упрощения оговариваются в условии задачи с самого начала, другие приходиться делать по мере ее решения. Таким образом, условие задачи уточняется, задача получает иную формулировку.

Анализируя задачу, необходимо определить, какие правила, формулы или закономерности следует применять в данной конкретной ситуации. А это составляет главную трудность для учащихся. При анализе задачи данные выделяться и то общее, что относит ее к тому или иному типу, и то особенное, что составляет ее характерную черту. Успешное усвоение общих правил и предписаний возможно только в процессе активной деятельности учащихся, особенно при решении проблемных и творческих задач.

Большое значение для формирования у учащихся навыков решения задач имеют единые требования к технике оформления записей, усвоение приемов рациональных вычислений и т д. Большинство задач нужно стараться решать в общем виде, а уже затем производить числовые расчеты. Числовые значения величин целесообразно подставлять в формулы с наименованиями. Это обязывает следить, чтобы все единицы величин были взяты в одной системе.

Следующий этап — выполнение вычислений. На них нередко тратят много времени. Происходит это главным образом из-за неумения применять математические знания на практике. Поэтому при решении задач на первый план нужно выдвигать физическую сторону вопроса, а затем искать пути и средства рациональных математических вычислений (например, приближенные вычисления)

В заключение проводят проверку и анализ решения. Сначала проверяют порядок полученной величины (с помощью прикидки) Такую проверку ответов должен постоянно делать учитель, приучая к этому и учащихся, которые нередко ошибаются в запятых, не имея навыков приближенных подсчетов.

Для проверки и анализа ответа важно логически оценить его правдоподобность, в том числе с помощью метода размерностей. Полезно и целесообразно в ряде задач использовать эксперимент или решить одну и ту же задачу нескольким способами.

 

Главные условия успешного решения задач:

1. Знание учащимися физических закономерностей

2.Правильное понимание физических величин, способов и единиц их измерений.

3.Математическая подготовка.

4.Знание некоторых общих и специальных приемов решения задач определенных типов (алгоритмов)

Классификация задач и методика решения задач разных типов.

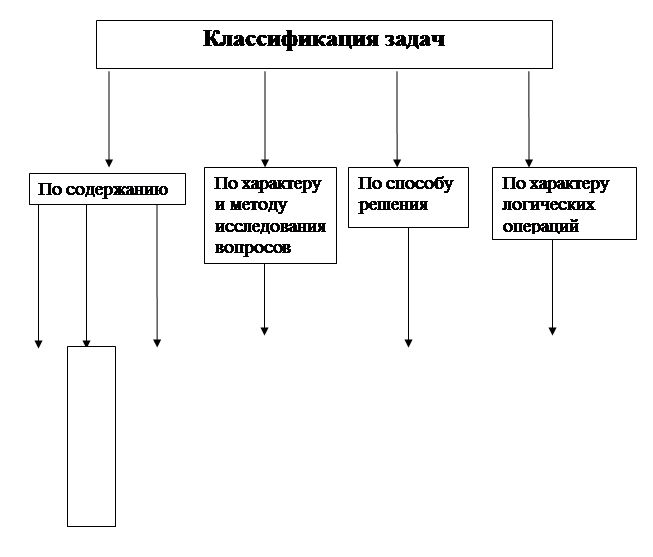
Задачи по физике классифицируют по многим признакам: по содержанию, назначению, глубине исследования вопроса, способам решения, способам задания условия, степени трудности и т.д.

По содержанию задачи следует разделить прежде в зависимости от их физического материала. Различают задачи по механике, молекулярной физике, электродинамике и т.д. Такое деление условно в том отношении, что нередко в условии задачи используются сведения из нескольких разделов физики.

Различают задачи с абстрактным и конкретным содержанием. Достоинство абстрактных задач состоит в том, что в них выделяется и подчеркивается физическая сущность, выяснению которой не мешают несущественные детали. Достоинство конкретных задач — большая наглядность и связь жизнью.

Задачи, содержащие материал о технике, промышленном и сельском — хозяйственном производстве, транспорте и связи, называют задачами с политехническим содержанием. Содержание политехнических задач должно быть тесно связано с изучаемым программным материалом. Рассматривая технический объект или, как правило, должны иметь широкое применение в народном хозяйстве. В задаче должны быть использованы реальные данные о машинах, процессах и т.д. и поставлены вопросы, которые действительно встречаются на практике. Технические задачи не только по содержанию, но и по форме должны, возможно, ближе подходить к условиям, встречающимися в жизни, где в задачах «ничего не дано», а необходимые данные приходиться брать из справочной литературы или из опытов.

Также есть задачи с историческим содержанием (где есть данные о классических физических опытах, открытиях, изобретениях). Широкое распространение получили занимательные задачи. Отличительная их черта — использование необычных, парадоксальных или занимательных фактов или явлений. Их решение оживляют урок, повышает интерес к физике. В зависимости от характера и методов исследований вопросов различают качественные и вычислительные задачи.

Качественными называют задачи, при решении которых устанавливают только качественную зависимость между физическими величинами. Как правило, вычисления при решении таких задач не производят. Иногда этот вид задач в методической литературе называют задачи – вопросы, логические задачи, качественные вопросы.

Эти задачи способствует развитию не только логического мышления, но и мыслительной деятельности в целом. Если задача не простая, то в ней надо связать не одно и не два физических явления. Хорошо эти задачи способствуют развитию умений применять свои теоретические знания на практике, они прекрасно развивают физическое мышление, а ребятам показывают, как в действительности физика нужна в жизни, являясь хорошим средством развития познавательного интереса.

Количественными называют задачи, при решении которых устанавливают количественную зависимость между величинами, а ответ получают в виде формулы или определенного числа.

По способу решения различают устные, экспериментальные, вычислительные и графические задачи. Деление это условно в том отношении, что при решении большинства задач применяют несколько способов.

Качественные задачи обычно используют как средство закрепления изученного материла. Во многих темах школьного курса физики качественные задачи являются основными. Очень популярны такого типа задачи при опросе, т.к. они дают возможность за короткое время выяснить усвоение физической сущности рассматриваемого вопроса. Успешное решение школьниками качественных задач показывает осознанность их знаний, отсутствие формализма в усвоении материала. Такие задачи весьма разнообразны по тематике, содержанию и сложности.

Решают качественные задачи, строя логические умозаключения, основанные на физических законах, с помощью индукции и дедукции. При решении этих задач анализ и синтез связаны так тесно между собой, что их иногда разделить нельзя, т.е. возможен только аналитико-синтетический способ рассуждений. Схема решения качественных задач такова:

1) чтение условия задачи, выяснение терминов в ее условии

2) анализ условия задачи, выяснение физических явлений, построение схемы или чертежа.

3) построение аналитико-синтетической цепи рассуждений

4) анализ полученного ответа с точки зрения его физического смысла, соответствия условию и реальности.

Условно все качественные задачи модно разделить на простые и сложные.

Качественными могут быть также и графические задачи, в которых объектом исследования являются графиком зависимости физических величин. В одних случаях эти графики заданы условием задачи, в других — их надо построить оп данным задачи.

Качественные графические задачи заключатся в основном в «чтении» и построении несложных графиков. Работу с графиками можно постепенно усложнять, предлагая учащимся находить и количественные зависимости между величинами, вплоть до составления формул. Если по этим формулам будут проводиться расчеты, то это будут уже вычислительные задачи.

Вычислительные задачи.Под вычислительными понимают задачи, в которых результат решения полуют с помощью вычислений и математических операций.

В зависимости от математических операций различают 4 способа решения задач: алгебраический, геометрический, тригонометрический и графический способы.

Решая физические задачи алгебраическим способом, используют формулы, составляют и решают алгебраические уравнения. Наиболее простой случай применения этого способа — решение задач по гонтовой формуле. В более сложных задачах окончательную зависимость, с помощью которой вычисляют несколько формул или систему уравнений.

При решении многих задач широко используют знания учащихся оп геометрии. Например, в статике, геометрической оптике, электростатике и в других разделах школьного курса физики решаются задачи, где необходимы чертежи, геометрические построения и использование известных учащимся геометрических соотношений. Во многих задачах, кроме геометрических соотношений, применяют и тригонометрические.

По характеру логических операций при решении физических вычислительных задач различают аналитический и синтетический методы.

При аналитическом методе решения задач начинают с выражения искомой величины через другие величины и, последовательно применяют физические формулы, определяя эту величину.

При синтетическом методе решения сначала устанавливают промежуточные зависимости между данными физическими величинами. В итоге всех операций, часть из которых может оказаться лишней, получают выражение, из которого и находят искомую величину.

Учащиеся чаще всего решают задачи синтетическим методом: ищут различные зависимости между величинами, пока не установят такую, которая дает возможность найти искомую величину. При этом, естественно, возможны пути, не приводящие к желаемому результату. Синтетический метод решения задач наиболее простой, но не всегда короткий. Аналитический метод труден, так как требует строгой логической последовательности в действиях. При решении задач, особенно в старших классах, предпочтительней аналитический метод, так, как он способствует развитию логического мышления.

При решении качественных задач, трудно выделить в чистом виде анализ или синтез, они выступают всегда во взаимосвязи. Поэтому и говорят об аналитико–синтетическом способе рассуждения при решении качественных задач.

 

Экспериментальные задачи и наблюдения.Характерная черта этого типа задач — использование при решении как лабораторного, так и демонстрационного эксперимента.

К этому же типу задач относятся и задачи-наблюдения. Учащиеся наблюдают за каким-то физическим явлением или процессом и отвечают на вопросы: «Что это за явление?». «Как его можно объяснить?» Это своего рода качественная задача — вопрос, но заданная экспериментально.

Лабораторные экспериментальные задачи — это разновидность фронтального эксперимента. Их отличительная черта — самостоятельное выполнение учащимися соответствующих опытов или наблюдений. Эти данные могут быть использованы и при решении экспериментальных задач.