Функция f (x), х є (а; b) называется непрерывной в точке х 0 є (а; b), если
предел функции f (x) в точке х 0 существует и равен значению функции в этой точке:
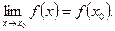
Согласно данному определению непрерывность функции f в точке х 0 означает выполнимость следующих условий:
1) функция f (х) должна быть определена в токе х 0;
2) у функции f (х) должен существовать предел в точке х 0
3) предел функции f (х) в точке х 0 совпадает со значением функции в этой точке.
Например, функция f (x) = х2 определена на всей числовой прямой и  Так как f (1) = = 1, т.е. значение f (x) = х 2в точке х = 1 совпадает с пределом при х → 1, то, согласно определению, функция f (x) = х 2 непрерывна в точке х = 1.
Так как f (1) = = 1, т.е. значение f (x) = х 2в точке х = 1 совпадает с пределом при х → 1, то, согласно определению, функция f (x) = х 2 непрерывна в точке х = 1.
Функция называется непрерывной в промежутке (замкнутом или открытом), если она непрерывна во всех точках этого промежутка.
Дадим другое определение непрерывности функции в точке.Функция  называется непрерывной в точке
называется непрерывной в точке  , если она в этой точке определена и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т.е.
, если она в этой точке определена и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т.е. 
Если функция  непрерывна в точке
непрерывна в точке  , то точка
, то точка  называется точкой непрерывности. В противном случае точка
называется точкой непрерывности. В противном случае точка  - называется точкой разрыва.
- называется точкой разрыва.
Если функция  имеет в точке
имеет в точке  разрыв, то для определения характера разрыва следует найти предел функции
разрыв, то для определения характера разрыва следует найти предел функции  при
при  слева и справа. В зависимости от характера поведения функции в окрестности точки разрыва различают 2 основных вида разрыва:
слева и справа. В зависимости от характера поведения функции в окрестности точки разрыва различают 2 основных вида разрыва:
1) разрыв I рода – в этом случае существуют конечные пределы 
2 ) разрыв II рода – в этом случае хотя бы один из пределов  или
или  не существует или бесконечен.
не существует или бесконечен.
Примеры по выполнению практической работы
Пример 1. Найти предел функции f(x) = |x| при x®0
Данная функция определена на всей числовой прямой. Так как f(x)=-x для х, удовлетворяющих неравенству x<0, то
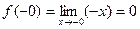 .
.
Так как f(x)=x, при x>0
 .
.
Таким образом, f(+0)=f(-0)=0. Так как односторонние пределы в точке нуль совпали, то предел функции f(x) в точке нуль существует и равен их общему значению, т.е.:
 .
.
Пример 2. Доказать, что функция  не имеет предела в точке х=1.
не имеет предела в точке х=1.
Данная функция определена на всей числовой прямой. Вычислим односторонние пределы этой функции в точке х=1:
 ,
,
 .
.
Итак, f(1-0)¹f(1+0). Следовательно, данная функция не имеет предела в точке х=1.
Пример 3. Исследовать на непрерывность функцию  в точке
в точке  .
.
Решение: воспользуемся определением 1:
1) Т.к.  определена на всей числовой прямой, то условие 1) выполнено;
определена на всей числовой прямой, то условие 1) выполнено;
2)  ;
;  ;
;
значит предел функции  в точке
в точке  существует и
существует и  .
.
3)  ;
;
Отсюда имеем, что  , т.е. предел функции при
, т.е. предел функции при  равен значению функции при
равен значению функции при  . Следовательно, функция
. Следовательно, функция  в точке х=3 непрерывна.
в точке х=3 непрерывна.
Пример 4. Исследовать на непрерывность функцию  в точке
в точке  .
.
Решение: опять воспользуемся определением 1:
1) в точке  функция не определена, значит нет выполнения первого условия, и непрерывности в точке
функция не определена, значит нет выполнения первого условия, и непрерывности в точке  нет.
нет.
Пример 5. Исследовать на непрерывность функцию 
Решение: функция  определена на всей числовой оси. В таких случаях удобно для исследования на непрерывность пользоваться вторым определением.
определена на всей числовой оси. В таких случаях удобно для исследования на непрерывность пользоваться вторым определением.
Дадим аргументу  приращение
приращение 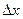 и найдем приращение функции
и найдем приращение функции  :
:

Найдем предел  при
при  :
: 
Т.к. равенство  справедливо при любом конечном значении
справедливо при любом конечном значении  , поэтому функция
, поэтому функция  непрерывна при любом значении
непрерывна при любом значении  .
.
Пример 6. Найти точки разрыва функций и определить их характер: а)  ; б)
; б)  .
.
Решение: а) т.к. в точке  функция
функция  не определена, значит ее точкой разрыва будет точка
не определена, значит ее точкой разрыва будет точка  . Для определения характера разрыва найдем левый и правый пределы функции при
. Для определения характера разрыва найдем левый и правый пределы функции при  :
:  ;
;  . Значит, функция
. Значит, функция  в точке
в точке  имеет разрыв II рода.
имеет разрыв II рода.
б) Функция  имеет единственную точку разрыва
имеет единственную точку разрыва  , в которой функция не определена. Вычислим односторонние пределы функции при
, в которой функция не определена. Вычислим односторонние пределы функции при 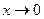 :
:  ;
;  . Т.к. левый и правый пределы функции в точке
. Т.к. левый и правый пределы функции в точке 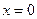 конечны, то точка
конечны, то точка 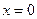 - точка разрыва I рода.
- точка разрыва I рода.
Задания для практического занятия:
Вариант 1
1. Указать, чему равны односторонние пределы в точке  функции f(x), заданной графиком:
функции f(x), заданной графиком:

2. Выяснить, существует ли предел функции f(x) в т.  , если
, если

3. Исследовать на непрерывность функцию:
а) y = 2x2 + 8x в точке x0 = -1; б) y = sin x на (-∞;+∞);
4. Найти точки разрыва функции и определить их характер:
а)  ; б)
; б)  ;
;
Вариант 2
1. Указать, чему равны односторонние пределы в точке  функции f(x), заданной графиком:
функции f(x), заданной графиком:

2. Выяснить, существует ли предел функции f(x) в т.  , если
, если

3. Исследовать на непрерывность функцию:
а) y = -2x2 + 5x в точке x0 = 2: б) y = x3 на (-∞;+∞)
4. Найти точки разрыва функции и определить их характер:
а)  ; б)
; б)  ;
;
Вариант 3
1. Указать чему равны односторонние пределы в т.  функции f(x), заданной графиком:
функции f(x), заданной графиком:

2. Выяснить, существует ли предел функции f(x) в т.  , если
, если

3. Исследовать на непрерывность функцию:
а) y = x2 + 7x в точке x0 = 3; б) y =sin 2x на (-∞;+∞);
4. Найти точки разрыва функции и определить их характер:
а)  ; б)
; б)  ;
;
Вариант 4
1. Указать чему равны односторонние пределы в т.  функции f(x), заданной графиком:
функции f(x), заданной графиком:

2. Выяснить, существует ли предел функции f(x) в т.  , если
, если

3. Исследовать на непрерывность функцию:
а) y = 4x2 – 3x + 1 в точке x0 = 2; б) y = cos 2x на (-∞;+∞);
4. Найти точки разрыва функции и определить их характер
а)  ; б)
; б) 
Контрольные вопросы
1. Дайте определение односторонних пределов функции;
2. Сформулируйте условие существования предела функции в точке;
3. Какая функция называется непрерывной в точке? На интервале?
4. Какие три условия необходимо проверить при исследовании функции на непрерывность?
5. Что такое точка непрерывности и точка разрыва?
6. Как определить характер точки разрыва?





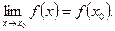
 Так как f (1) = = 1, т.е. значение f (x) = х 2в точке х = 1 совпадает с пределом при х → 1, то, согласно определению, функция f (x) = х 2 непрерывна в точке х = 1.
Так как f (1) = = 1, т.е. значение f (x) = х 2в точке х = 1 совпадает с пределом при х → 1, то, согласно определению, функция f (x) = х 2 непрерывна в точке х = 1. называется непрерывной в точке
называется непрерывной в точке  , если она в этой точке определена и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т.е.
, если она в этой точке определена и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т.е. 
 непрерывна в точке
непрерывна в точке  слева и справа. В зависимости от характера поведения функции в окрестности точки разрыва различают 2 основных вида разрыва:
слева и справа. В зависимости от характера поведения функции в окрестности точки разрыва различают 2 основных вида разрыва:
 или
или  не существует или бесконечен.
не существует или бесконечен.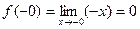 .
. .
. .
. не имеет предела в точке х=1.
не имеет предела в точке х=1. ,
, .
. в точке
в точке  .
. ;
;  ;
; .
. ;
; , т.е. предел функции при
, т.е. предел функции при  равен значению функции при
равен значению функции при  . Следовательно, функция
. Следовательно, функция  в точке х=3 непрерывна.
в точке х=3 непрерывна. в точке
в точке  .
. функция не определена, значит нет выполнения первого условия, и непрерывности в точке
функция не определена, значит нет выполнения первого условия, и непрерывности в точке 
 определена на всей числовой оси. В таких случаях удобно для исследования на непрерывность пользоваться вторым определением.
определена на всей числовой оси. В таких случаях удобно для исследования на непрерывность пользоваться вторым определением. приращение
приращение 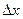 и найдем приращение функции
и найдем приращение функции  :
:
 :
: 
 непрерывна при любом значении
непрерывна при любом значении  ; б)
; б)  .
. :
:  ;
;  . Значит, функция
. Значит, функция  , в которой функция не определена. Вычислим односторонние пределы функции при
, в которой функция не определена. Вычислим односторонние пределы функции при 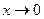 :
:  ;
;  . Т.к. левый и правый пределы функции в точке
. Т.к. левый и правый пределы функции в точке 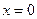 конечны, то точка
конечны, то точка  функции f(x), заданной графиком:
функции f(x), заданной графиком:
 , если
, если
 ; б)
; б)  ;
; функции f(x), заданной графиком:
функции f(x), заданной графиком:

 ; б)
; б)  ;
;
 , если
, если
 ; б)
; б)  ;
; функции f(x), заданной графиком:
функции f(x), заданной графиком:
 , если
, если
 ; б)
; б) 



