Практическая работа № 8
Тема: « Вычисление определителей, ранга матриц. »
Цель работы: научиться выполнять действия над матрицами, вычислять определители.
Образовательные результаты, заявленные во ФГОС:
Студент должен
уметь:
- выполнять операции над матрицами.
знать:
- основы математического анализа, линейной алгебры и аналитической геометрии.
Оборудование: рабочая тетрадь, ручка, методические рекомендации по выполнению практической работы, справочная литература.
Методические указания по выполнению работы:
1. Ознакомиться с теоретическим материалом по практической работе.
2. Рассмотрите образцы решения задач по теме.
3.Выполнить предложенное задание согласно варианту по списку группы.
4.Изучить условие заданий для практической работы и выполнить её.
5. Ответить на контрольные вопросы даются письменно, после решения заданий в тетради для практических работ. Во время выполнения работы обучающийся может пользоваться своим конспектом, а также учебной литературой и справочным материалом.
5. Оформить отчет о работе. Сделайте вывод.
Краткие теоретические и учебно-методические материалы по теме практической работы
Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины (или n столбцов одинаковой длины). Матрица записывается в виде

или сокращенно:  , где
, где  (т.е.
(т.е.  ) – номер строки,
) – номер строки,  (т.е.
(т.е. 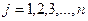 ) - номер столбца. Матрицу
) - номер столбца. Матрицу  называют матрицей размера
называют матрицей размера  и пишут
и пишут  . Числа
. Числа  , составляющие матрицу, называются ее элементами. Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной и обозначается
, составляющие матрицу, называются ее элементами. Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной и обозначается  .
.
Действия над матрицами
Сложение
Операция сложения матриц вводится только для матриц одинаковых размеров.
Суммой двух матриц  и
и 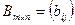 называется матрица
называется матрица  такая, что
такая, что
 (
( ,
,  ).Аналогично определяется разность матриц.
).Аналогично определяется разность матриц.
Умножение вектора на число
Произведением матрицы  на число k называется матрица
на число k называется матрица 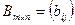 такая, что
такая, что  (
( ,
,  ).
).
Произведение матриц
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы. Произведением матрицы  на матрицу
на матрицу 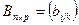 называется матрица
называется матрица 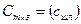 такая, что
такая, что
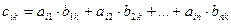 , где
, где  ,
, 
т. е. элемент i -й строки и k -го столбца матрицы произведения С равен сумме произведений элементов i -й строки матрицы А на соответствующие элементы k -го столбца матрицы В.
Тогда произведение  не определено, так как число столбцов матрицы А (их 3) не совпадает с числом строк матрицы В (их 2). При этом определено произведение
не определено, так как число столбцов матрицы А (их 3) не совпадает с числом строк матрицы В (их 2). При этом определено произведение  , которое считают следующим образом:
, которое считают следующим образом:

Умножение матриц обладает следующими свойствами:
1.  3.
3. 
2.  4.
4. 
Определитель матрицы
Квадратной матрице А порядка n можно сопоставить число det А (или  , или
, или 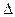 ), называемое ее определителем, следующим образом:
), называемое ее определителем, следующим образом:
1. 
2. 
3. 

Свойства определителей
Если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.
Свойство1. («Элементарные преобразования определителей»). Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число.
Минором некоторого элемента  определителя n -го порядка называется определитель n - 1-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается
определителя n -го порядка называется определитель n - 1-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается  . Так если:
. Так если:
 то
то 

Алгебраическим дополнением элемента  определителя называется его минор, взятый со знаком «плюс», если сумма
определителя называется его минор, взятый со знаком «плюс», если сумма  четное число, и со знаком «минус», если эта сумма нечетная. Обозначается
четное число, и со знаком «минус», если эта сумма нечетная. Обозначается  .
.

Свойство 2. («Разложение определителя по элементам некоторого ряда»).
Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения. В случае определителей 3-го порядка свойство 7 означает, что

Квадратная матрица А называется невырожденной, если определитель ∆ = det A ≠0. В противном случае (∆ = 0) матрица А называется вырожденной.
Союзная и обратная матрицы
Матрицей союзной к матрице А называется матрица:
A*=  ,
,
где А  - алгебраическое дополнение элемента а
- алгебраическое дополнение элемента а  данной матрицы А. Матрица А
данной матрицы А. Матрица А  называется обратной матрице А, если выполняется условие А·А
называется обратной матрице А, если выполняется условие А·А  = А
= А  · А = Е,
· А = Е,
где Е – единичная матрица того же порядка, что и матрица А.
Пусть А – невырожденная матрица
A = 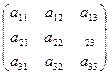 , и det A ≠0.
, и det A ≠0.
Составим союзную матрицу
A *= 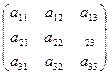
Тогда A  =
= 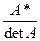 , т.е. A
, т.е. A  =
=  ·
·  .
.
Отметим свойства обратной матрицы:
- det(A
 ) =
) =  ;
; - (A·B)
 = B
= B  · A
· A  ;
; - (A
 )
)  = (A
= (A  )
)  .
.
Пример по выполнению практической работы
Пример 1. 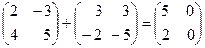
Пример 2. 
Пример 3.  .
.
Пример 4. Найти определитель матрицы  .
.
Решение: 
Пример 5. Вычислить определитель

Ответ: =4.
Пример 7. Найти А  , если
, если 
Решение: 

Составим союзную матрицу. Для этого вычислим алгебраические дополнения:



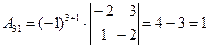


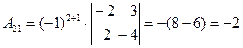


Союзная матрица будет следующей:  . Вычислим обратную матрицу:
. Вычислим обратную матрицу:


Проверкой  убеждаемся, что обратная матрица найдена верно.
убеждаемся, что обратная матрица найдена верно.
Задания для практического занятия:
Даны матрицы А и В. Найти:
- A + B, A - B
- C =2 A -3 B
- AB; BA
- det A; det B
- A ‾ ¹, B ‾ ¹. Проверить правильность их нахождения умножением
 :
:
Вариант 1 Вариант 2
A =  ; B =
; B =  ; A =
; A =  ; B =
; B = 
Вариант 3 Вариант 4
A =  ; B =
; B =  ; A =
; A =  ; B =
; B =  ;
;
Контрольные вопросы
1. Что называется матрицей? Дать определения основных понятий матрицы;
2. Какая матрица называется квадратной? Единичной?
3. Какие операции можно производить над матрицами?
4. Что такое определитель матрицы? Перечислите его свойства;
5. Как вычислить минор и алгебраическое дополнение элемента  матрицы А?
матрицы А?
7. Как найти союзную и обратную матрицы для матрицы А?
Практическая работа № 9
«Решение систем линейных уравнений методом обратных матриц»
Цель работы: научиться решать системы линейных уравнений методом обратной матрицы.
Образовательные результаты, заявленные во ФГОС третьего поколения:
Студент должен
уметь:
- решать системы линейных уравнений.
знать:
- основы математического анализа, линейной алгебры и аналитической геометрии.
Оборудование: рабочая тетрадь, ручка, методические рекомендации по выполнению практической работы, справочная литература.
Методические указания по выполнению работы:
1. Ознакомиться с теоретическим материалом по практической работе.
2. Рассмотрите образцы решения задач по теме.
3.Выполнить предложенное задание согласно варианту по списку группы.
4.Изучить условие заданий для практической работы и выполнить её.
5. Ответить на контрольные вопросы даются письменно, после решения заданий в тетради для практических работ. Во время выполнения работы обучающийся может пользоваться своим конспектом, а также учебной литературой и справочным материалом.
5. Оформить отчет о работе. Сделайте вывод.






 , где
, где  (т.е.
(т.е.  ) – номер строки,
) – номер строки,  (т.е.
(т.е. 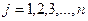 ) - номер столбца. Матрицу
) - номер столбца. Матрицу  называют матрицей размера
называют матрицей размера  и пишут
и пишут  . Числа
. Числа  , составляющие матрицу, называются ее элементами. Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной и обозначается
, составляющие матрицу, называются ее элементами. Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной и обозначается  .
. и
и 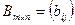 называется матрица
называется матрица  такая, что
такая, что (
( (
(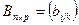 называется матрица
называется матрица 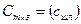 такая, что
такая, что 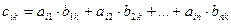 , где
, где 
 не определено, так как число столбцов матрицы А (их 3) не совпадает с числом строк матрицы В (их 2). При этом определено произведение
не определено, так как число столбцов матрицы А (их 3) не совпадает с числом строк матрицы В (их 2). При этом определено произведение  , которое считают следующим образом:
, которое считают следующим образом:
 3.
3. 
 4.
4. 
 , или
, или 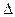 ), называемое ее определителем, следующим образом:
), называемое ее определителем, следующим образом:



 . Так если:
. Так если: то
то 

 четное число, и со знаком «минус», если эта сумма нечетная. Обозначается
четное число, и со знаком «минус», если эта сумма нечетная. Обозначается  .
.

 ,
, - алгебраическое дополнение элемента а
- алгебраическое дополнение элемента а  называется обратной матрице А, если выполняется условие А·А
называется обратной матрице А, если выполняется условие А·А 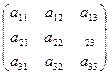 , и det A ≠0.
, и det A ≠0.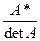 , т.е. A
, т.е. A  ·
·  .
. = (A
= (A 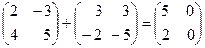

 .
. .
.







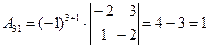


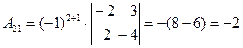


 . Вычислим обратную матрицу:
. Вычислим обратную матрицу:

 убеждаемся, что обратная матрица найдена верно.
убеждаемся, что обратная матрица найдена верно. :
: ; B =
; B =  ; A =
; A =  ; B =
; B = 
 ; B =
; B =  ; A =
; A =  ; B =
; B =  ;
;


