| t
|
| 0.4
| 0.8
| 1.2
| 1.6
| 2.0
| 2.4
|
|
| 0.64
| 0.74
| 0.62
| 0.59
| 0.35
| -0.09
| -0.39
|
|
| 0.54
| 0.37
| 0.06
| -0.32
| -0.60
| -0.69
| -0.67
|
|
| 0.34
| 0.50
| 0.37
| 0.26
| -0.52
| -0.72
| 0.42
|
|
| 0.23
| 0.26
| 0.35
| 0.55
| 0.69
| 0.75
| 0.80
|
|
| 0.12
| 0.20
| 0.24
| 0.18
| -0.20
| -0.42
| -0.46
|
|
| -0.16
| -0.12
| -0.15
| 0.05
| 0.29
| 0.43
| 0.63
|
|
| -0.22
| -0.29
| -0.38
| -0.24
| -0.06
| 0.07
| -0.16
|
|
| -0.26
| -0.69
| -0.70
| -0.61
| -0.43
| -0.22
| 0.29
|
|
| -0.30
| -0.60
| -0.68
| -0.62
| -0.68
| -0.56
| -0.54
|
|
| -0.50
| 0.13
| 0.75
| 0.84
| 0.78
| 0.73
| 0.71
|
|
| -0.69
| -0.40
| 0.08
| 0.16
| 0.12
| 0.18
| 0.33
|
|
| 0.18
| -0.79
| -0.56
| -0.39
| -0.42
| -0.58
| -0.53
|
Описание метода.
1.1Характеристики и свойства случайных процессов.
Явления, в которых случайность проявляется в форме процесса, называются случайными процессами. На практике такие процессы проявляются в виде случайных величин, непрерывно изменяющихся в ходе опыта. В отличие от обычных случайных величин их принято называть случайными функциями. Изучением случайных функций занимается специальная отрасль теории вероятности - теория случайных или стохастических процессов, которую можно образно назвать «динамикой случайных явлений».
Случайной называется функция, которая в результате опыта может принять тот или иной конкретный вид, неизвестно заранее - какой именно.
Для обозначения случайной функции обычно используется символ Х(t), где аргумент t чаще всего трактуется как время.
Конкретный вид, принимаемый случайной функцией в результате опыта, называется реализацией. Реализация является обычной, неслучайной функцией. Группа опытов дает семейство реализаций. В общем случае случайная функция может представлять собой случайную величину, зависящую от многих аргументов.
Очевидно, что на графике можно изобразить только реализации случайной функции, как это показано на рис.1.
Реализации случайной функции

Рис.1
Если зафиксировать, как показано на рисунке, значение аргумента, то получим реализации случайной величины, в которую превращается случайная функция при зафиксированном значении аргумента. Эта случайная величина называется сечением случайной функции.
Таким образом, случайная функция совмещает в себе черты случайной величины и функции. Поэтому ее можно трактовать как систему большого числа случайных величин:
Х(t)®(X(t1),..., X(tk),..., X(tm)).
Чем больше случайных величин X(tk) включает в себя эта система, тем полнее она представляет случайную функцию.
Следовательно, в качестве исчерпывающей вероятностной характеристики случайной функции может использоваться закон совместного распределения элементов вышеуказанной системы при достаточно большом их числе. Очевидно, что практически воспользоваться таким законом невозможно, в силу чего на практике используются характеристики случайной функции, подобные числовым характеристикам случайных величин: математическое ожидание mx(t), дисперсия Dx(t) и корреляционная функция Kx(t,t`).
Математическим ожиданием случайной функции X(t) называется неслучайная функция mx(t), которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения случайной функции.
Дисперсией случайной функции Х(t) называется неслучайная функция Dx(t), значение которой для каждого t равно дисперсии соответствующего сечения случайной функции.
Как и для случайной величины, корень квадратный из дисперсии дает функцию sх(t) - среднее квадратичное отклонение случайной функции.
Корреляционной функцией случайной функции X(t) называется неслучайная функция двух аргументов Kx(t,t`), которая при каждой паре значений t,t` равна корреляционному моменту соответствующих сечений случайной функции:
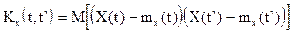
Корреляционная функция является мерой стохастической зависимости между двумя сечениями случайной функции. Чем больше ее значение, тем теснее стохастическая связь.
По определению, Kx(t,t`)=Kx(t`,t), т.е. корреляционная функция симметрична относительно своих аргументов. Кроме того:
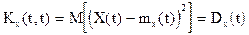 ,
,
т.е. дисперсия случайной функции является частным случаем ее корреляционной функции, в силу чего отпадает необходимость в дисперсии как отдельной характеристике.
Отмеченные свойства корреляционной функции являются основными.
На практике удобно пользоваться нормированной корреляционной функцией, которая определяется зависимостью:
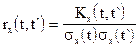 .
.
Очевидно, что 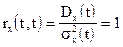 .
.
Так как от случайной функции X(t) всегда можно перейти к центрированной случайной функции 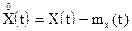 , для которой математическое ожидание равно нулю, то становится ясным, что корреляционная функция, включающая в себя ее дисперсию как частный случай, является единственной существенной характеристикой случайных процессов. Поэтому ее определению всегда уделяется повышенное внимание. С этой точки зрения важно различать нестационарные и стационарные случайные процессы. Для первых характерно то, что они имеют определенную тенденцию развития во времени. Примером такого процесса может служить процесс изменения давления в канале ствола артиллерийского орудия. Все характеристики таких процессов являются функциями времени. Стационарные процессы протекают во времени приблизительно однородно и имеют вид непрерывных колебаний относительно некоторого среднего значения.
, для которой математическое ожидание равно нулю, то становится ясным, что корреляционная функция, включающая в себя ее дисперсию как частный случай, является единственной существенной характеристикой случайных процессов. Поэтому ее определению всегда уделяется повышенное внимание. С этой точки зрения важно различать нестационарные и стационарные случайные процессы. Для первых характерно то, что они имеют определенную тенденцию развития во времени. Примером такого процесса может служить процесс изменения давления в канале ствола артиллерийского орудия. Все характеристики таких процессов являются функциями времени. Стационарные процессы протекают во времени приблизительно однородно и имеют вид непрерывных колебаний относительно некоторого среднего значения.
Вероятностные характеристики таких процессов не зависят от времени, т.е. mx=const, Dx=const, а корреляционная функция является функцией только одно аргумента, равного t=t`-t, в связи с чем она обозначается через kx(t). Последнее означает, что величина корреляционной функции процесса зависит только от удаленности сечений X(t) и X(t`) и не зависит от того, на каком участке временной оси эти сечения выбраны. Соответственно нормированная корреляционная функция стационарных процессов определяется как
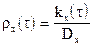 .
.
Так как 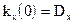 , то
, то 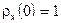 .
.
Таким образом, для стационарных процессов построение корреляционной функции облегчается.
1.2 Определение характеристик случайных процессов по результатам испытаний.
Пусть над случайной функцией X(t) произведено n независимых опытов и получено n реализаций процесса. Требуется найти оценки для вероятностных характеристик mx(t), Dx(t) и Kx(t,t`). Для этого рассматривается ряд сечений случайной функции для моментов времени t1,t2,..., tk,..., tl,..., tm и регистрируются значения, принятые функцией Х(t) в эти моменты времени. Каждому из моментов t1,..., tm будет соответствовать n значений случайной величины (на рис.1.6 - значения x1, x2, x3). Значения t1,..., tm обычно задаются равноотстоящими, а величина интервала между соседними точками выбирается в зависимости от вида опытных кривых так, чтобы сохранить основную тенденцию процесса, т.е. чтобы по выбранным точкам можно было восстановить основной ход кривых.
Зарегистрированные значения функции X(t) заносятся в таблицу, каждая строка которой соответствует одной реализации (всего n строк), а число столбцов равно числу опорных значений аргумента (всего m с толбцов). Очевидно, что в таком виде таблица будет представлять результаты n опытов над системой m случайных величин. Обработка данных такой таблицы ведется в последовательности:
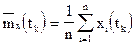 ,
,
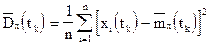 ,
,
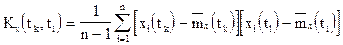
Результаты расчетов удобно представить а виде таблицы 2
Результаты определения характеристик процесса X(t)
Таблица 2
| t
| t1
| ...
| tk
| ...
| tl
| ...
| tm
|
| t1
| 
| ...
| 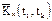
| ...
| 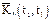
| ...
| 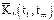
|
| ...
| ..
| ...
| ...
| ...
| ...
| ...
| ...
|
| tk
| ...
| ...
| 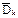
| ...
| 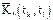
| ...
| 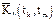
|
| ...
| ...
| ...
| ...
| ...
| ...
| ...
| ...
|
| tl
| ...
| ...
| ...
| ...
| 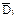
| ...
| 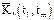
|
| ...
| ...
| ...
| ...
| ...
| ...
| ...
| ...
|
| tm
| ...
| ...
| ...
| ...
| ...
| ...
| 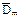
|
Как видно, по главной диагонали таблицы расположены оценки дисперсии соответствующих сечений, а на диагоналях, параллельных главной, содержатся оценки корреляционной функции:
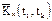 ,...,
,..., 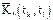 ,...,
,..., 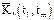 .
.
Если процесс является стационарным, то наблюдающиеся различия между этими оценками нельзя считать значимыми, т.к. в силу ограниченности числа реализаций они содержат большой элемент случайности. В таком случае их следует осреднить по каждой из параллелей и получить таким образом оценки корреляционной функции стационарного процесса 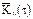 .
.
Рекомендации по выполнению работы.
Вариант исходных данных генерируется при выборе пункта меню «Файл»-«Новый». Все необходимые вычисления производятся при нажатии кнопки «Расчет». В окне появляется графическое представление реализаций случайного процесса. При нажатии кнопки «Button2» в окне появляется графическое представление рассчитанной нормированной корреляционной функции.
1. Определение МОЖ процесса mx(t ): суммируем значения по столбцам и делим на n =12. Заполняем таблицу 2:
Таблица 2
Функция mx(t).
| t
|
| 0.4
| 0.8
| 1.2
| 1.6
| 2.0
| 2.4
|
|
| -0.07
| -0.057
| 0.00
| 0.037
| -0.057
| -0.093
| 0.036
|
2. Определение корреляционной функции Kx(t,t'):
2.1. Вычисляются дисперсии в каждом сечении: суммируются квадраты чисел, стоящих в соответствующих столбцах; сумма делится на n =12; из результата вычитается квадрат соответствующего математического ожидания- получается статистическая дисперсия; для получения несмещенной оценки дисперсии результат умножается на поправку n/(n-1) =12/11. Полученные значения размещаются по главной диагонали матрицы (табл.3).
2.2.2. Вычисляются корреляционные моменты: для вычисления момента, отвечающего двум заданным сечениям, перемножаются числа, стоящие в соответствующих столбцах, произведения складываются алгебраически, полученная сумма делится на n =12, из результата вычитается произведение соответствующих математических ожиданий; для получения несмещенной оценки момента результат умножается на n/(n-1) =12/11. Полученные значения размещаются по диагоналям матрицы (табл. 3).
Таблица 3
Функция Kx(t,t').
| t
|
| 0.4
| 0.8
| 1.2
| 1.6
| 2.0
| 2.4
|
|
| 0.1632
| 1.1379
| 0.0795
| 0.0457
| -0.0106
| -0.0642
| -0.0648
|
| 0.4
|
| 0.2385
| 0.2029
| 0.1621
| 0.0827
| 0.0229
| 0.0251
|
| 0.8
|
|
| 0.2356
| 0.2152
| 0.1527
| 0.0982
| 0.0896
|
| 1.2
|
|
|
| 0.2207
| 0.1910
| 0.1491
| 0.1322
|
| 1.6
|
|
|
|
| 0.2407
| 0.2348
| 0.1711
|
| 2.0
|
|
|
|
|
| 0.2691
| 0.2114
|
| 2.4
|
|
|
|
|
|
| 0.2878
|
По главной диагонали таблицы 3 стоят дисперсии:
| t
|
| 0.4
| 0.8
| 1.2
| 1.6
| 2.0
| 2.4
|
| Dx(t)
| 0.1632
| 0.2385
| 0.2356
| 0.2207
| 0.2407
| 0.2691
| 0.2878
|
Извлекая из этих величин квадратные корни, находим зависимость среднего квадратического отклонения sx от времени:
| t
|
| 0.4
| 0.8
| 1.2
| 1.6
| 2.0
| 2.4
|
| sx (t)
| 0.404
| 0.488
| 0.485
| 0.470
| 0.491
| 0.519
| 0.536
|
Деля значения, стоящие в табл.3, на произведения соответствующих sx(t) получим таблицу значений нормированной корреляционной функции rx(t,t'):
Таблица 4
Нормированная корреляционная функция rx(t,t')
| t
t’
|
| 0.4
| 0.8
| 1.2
| 1.6
| 2.0
| 2.4
|
|
|
| 0.700
| 0.405
| 0.241
| -0.053
| -0.306
| -0.299
|
| 0.4
|
|
| 0.856
| 0.707
| 0.345
| 0.090
| 0.095
|
| 0.8
|
|
|
| 0.943
| 0.643
| 0.390
| 0.344
|
| 1.2
|
|
|
|
| 0.829
| 0.612
| 0.524
|
| 1.6
|
|
|
|
|
| 0.923
| 0.650
|
| 2.0
|
|
|
|
|
|
| 0.760
|
| 2.4
|
|
|
|
|
|
|
|
Проанализируем полученные данные под углом зрения предполагаемой стационарности случайной функции X(t). Если судить непосредственно по данным, полученным в результате обработки, то можно придти к выводу, что случайная функция стационарной не является: ее матиматическое ожидание не вполне постоянно, дисперсия также несколько меняется со временем, значения нормированной корреляционной функции вдоль параллелей главной диагонали (табл.4) также не вполне постоянны. Однако, принимая во внимание весьма ограниченное число обработанных реализаций (n =12) и в связи с этим наличие большого элемента случайности в статических характеристиках, эти видимые отступления от стационарности вряд ли можно считать значимыми, тем более, что они не носят сколько-нибудь закономерного характера. Поэтому вполне целесообразно будет замена функции X(t) стационарной функцией. Для приведения функции X(t) к стационарной прежде всего осредним по времени математические ожидания в сечениях:
mx=1/7(mx(0)+mx(0.4)+.... +mx(2.4)) = 0.02
Аналогично:
Dx=1/7(Dx(0)+Dx(0.4)+.... +Dx(2.4)) = 0.236
sx =_Dx = 0.486
Перейдем к построению нормированной корреляционной функции того стационарного процесса, которым можно заменить функцию X(t). Для стационарного процесса корреляционная функция (а значит и нормированная корреляционная функция) зависит только от t=t'-t.
Следовательно, при постоянном t корреляционная функция должна быть постоянной. В табл.4 постоянному соответствуют: главная диагональ (t=0) и параллели этой диагонали (t=0.4; t=0.8; t=1.2 и т.д.). Осредняя значения нормированной корреляционной функции вдоль этих параллелей главной диагонали, получим значения функции rx(t):
Таблица 5




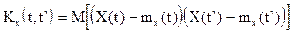
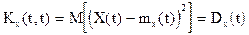 ,
,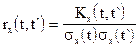 .
.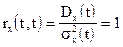 .
.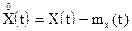 , для которой математическое ожидание равно нулю, то становится ясным, что корреляционная функция, включающая в себя ее дисперсию как частный случай, является единственной существенной характеристикой случайных процессов. Поэтому ее определению всегда уделяется повышенное внимание. С этой точки зрения важно различать нестационарные и стационарные случайные процессы. Для первых характерно то, что они имеют определенную тенденцию развития во времени. Примером такого процесса может служить процесс изменения давления в канале ствола артиллерийского орудия. Все характеристики таких процессов являются функциями времени. Стационарные процессы протекают во времени приблизительно однородно и имеют вид непрерывных колебаний относительно некоторого среднего значения.
, для которой математическое ожидание равно нулю, то становится ясным, что корреляционная функция, включающая в себя ее дисперсию как частный случай, является единственной существенной характеристикой случайных процессов. Поэтому ее определению всегда уделяется повышенное внимание. С этой точки зрения важно различать нестационарные и стационарные случайные процессы. Для первых характерно то, что они имеют определенную тенденцию развития во времени. Примером такого процесса может служить процесс изменения давления в канале ствола артиллерийского орудия. Все характеристики таких процессов являются функциями времени. Стационарные процессы протекают во времени приблизительно однородно и имеют вид непрерывных колебаний относительно некоторого среднего значения.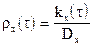 .
.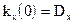 , то
, то 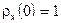 .
.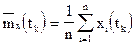 ,
,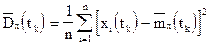 ,
,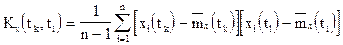
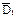
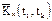
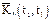
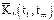
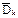
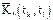
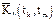
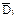
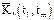
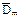
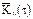 .
.

