Лабораторный практикум
по дисциплине
“Испытания изделий”
Методические указания
Санкт-Петербург
2015г
Оглавление
Введение. 2
Лабораторная работа № 1. 3
Обоснование статистических решений. Сравнение методов Байеса и минимакса. 3
Постановка задачи. 3
Описание методов: 4
Метод Байеса: 4
Минимаксный принцип. 6
Формирование расчетных алгоритмов. 7
Алгоритм на основе байесовского принципа. 7
Алгоритм на основе минимаксимального принципа. 8
Рекомендации по выполнению работы. 10
Варианты заданий. 12
Пример оформления отчета по лабораторной работе №1. 13
Лабораторная работа № 2. 16
Проверка статистических гипотез о законах распределения. Определение гарантированной скорости предела сквозного пробития Vпсп методом статистических испытаний. 16
Постановка задачи. 16
Описание метода. 17
Рекомендации по выполнению работы. 19
Варианты заданий. 23
Пример оформления отчета по лабораторной работе №2. 24
Лабораторная работа №3. 27
Определение характеристик случайных процессов. 27
Постановка задачи. 27
Описание метода. 27
Рекомендации по выполнению работы. 31
Пример оформления отчета по лабораторной работе №3. 34
Лабораторная работа № 4. 38
Планирование эксперимента. Регрессионный анализ. 38
Постановка задачи. 38
Описание метода. 39
Рекомендации по выполнению работы. 40
Пример оформления отчета по лабораторной работе №4. 41
Приложение 1. 46
Приложение 2. 47
Приложение 3. 48
Приложение 4. 48
Приложение 5. 48
Литература: 49
Введение
Лабораторный практикум по курсу “ИСПЫТАНИЯ ИЗДЕЛИЙ” состоит из четырех лабораторных работ. Комплект типовых заданий: 40 вариантов приведен в методических указаниях по выполнению лабораторных работ.
Л.р. №1 “Обоснование статистических решений”.
Л.р. №2 “Проверка статистических гипотез о законах распределения”.
Л.р. №3 “Определение характеристик случайных процессов”.
Л.р. №4 “Планирование эксперимента”.
Отчеты по лабораторным работам представляются в печатной или рукописной форме.
Отчет состоит из двух частей:
- Часть 1. Симуляция и сбор статистики на имитационной модели.
- Часть 2. Анализ и обработка полученной информации.
Выдача – 2, 6, 10, 14 неделя, сдача и защита – 3, 7, 11 и 15 неделя.
Для выполнения части 1 используются имитационные стохастические компьютерные модели.
Часть 2 лабораторных работ выполняется с целью ознакомления студентов с методами статистической обработки результатов испытаний изделий.
Нормы трудоемкости на выполнение ЛР не превышают установленные нормативы (не более 2-3 часов в неделю, продолжительность выполнения не более 7 недель).
Подготовка и защита лабораторных работ
Объем лабораторных работ – не менее 3 стр. Обязательно использование электронных баз данных.
Процедура защиты лабораторных работ: выступление с устной презентацией результатов с последующим групповым обсуждением, ответы на вопросы преподавателя.
Критерии оценивания
· соответствие содержания заявленной теме, отсутствие в тексте отступлений от темы;
· соответствие целям и задачам дисциплины;
· постановка проблемы, корректное изложение смысла основных используемых методов, их теоретическое обоснование и объяснение;
· логичность и последовательность в изложении материала;
· способность к работе с литературными источниками, Интернет-ресурсами, справочной и энциклопедической литературой;
· объем исследованной литературы и других источников информации;
· владение иностранными языками, использование иностранных источников;
· способность к анализу и обобщению информационного материала, степень полноты обзора состояния вопроса;
· умение извлекать информацию, соответствующую поставленной цели, и перераспределять информацию;
· навыки планирования и управления временем при выполнении работы;
· обоснованность выводов;
· правильность оформления (соответствие стандарту, структурная упорядоченность, ссылки, цитаты, таблицы и т.д.);
· соблюдение объема, шрифтов, интервалов (соответствие оформления правилам компьютерного набора текста).
Лабораторная работа № 1.
Обоснование статистических решений. Сравнение методов Байеса и минимакса.
Цель работы: Практическое применение методов обоснования статистических решений, основанных на байесовском риске. Сравнение методов Байеса и минимакса.
Постановка задачи.
Пусть производится диагностика состояния гидроцилиндра двигателя по содержанию железа в масле (параметр x). Задача состоит в выборе значения x0 параметра x таким образом, что при x > x0 следует принимать решение о снятии двигателя с эксплуатации, а при x< x0 допускать дальнейшую работу.
Так как состояние системы характеризуется одним параметром, то система имеет одномерное пространство признаков, а область возможных решений содержит две подобласти: x< x0 и x > x0. Первой подобласти соответствуют исправное состояние системы w1 и решение d1, а второй - неисправное состояние w2 и решение d2 т.е.
при x< x0 полагаем x  d1,
d1,
при x< x0 полагаем x  d2.
d2.
Но по причине влияния многих факторов признак x является величиной случайной, имеющей свой закон распределения в каждой из этих подобластей, что показано на рис. 1.
Рис.1
Как видно из рисунка 1, плотности распределений пересекаются, так что кривая f(x/d1) частично попадает в область дефектного состояния и наоборот - кривая f(x/d2) частично расположена в области исправного состояния. Это означает, что параметр x неоднозначно характеризует состояние системы, в силу чего возможны ошибки в принятии решения по результатам измерения параметра x: ошибка 1-го рода a, когда система в действительности исправна, но принимается решение d2, и ошибка 2-го рода b, когда система дефектна, но принимается решение d1. Следовательно, граничное значение x0 должно быть выбрано таким образом, чтобы последствия этих ошибок оказались приемлемыми с практической точки зрения.
Для получения такого решения необходимо конкретизировать условие задачи.
Пусть f(x/d) является плотностью нормального распределения с параметрами:
_
x1 - 5 г (5 г железа на I тонну масла),
S1 - 2 г,
_
x2 - 12 г,
S2 - 3 г,
Кроме того на основе анализа статистических данных установлено, что вероятность исправного состояния гидроцилиндра P1= 0,9, т.е. P2= 1- P1= 0,1.
Примем также, что:
C11= C22= 0,
C12= 1,
C22= 20,
т.е. цена ошибки второго рода (цена пропуска дефекта) в 20 раз больше цены ошибки 1-го рода (цены ложной тревоги).
При этих исходных данных необходимо определить граничное значение x0 и величину риска, используя байесовский принцип и принцип минимакса.
Описание методов:
Метод Байеса:
Рассмотрим случай, когда технический объект подвергается испытанию с целью определить возможность его дальнейшего использования. При такой постановке задачи фактически предполагается 2 возможных состояния:
w1 - объект работоспособен; вероятность - Р1;
w2 - объект не работоспособен; вероятность - Р2.
Р1 и Р2 известны нам, еще до проведения испытаний.
Соответственно и множество возможных решений D будет двухкомпонентным D{d1,d2}:
d1 - объект находится в состоянии w1;
d2 - объект находится в состоянии w2.
Пусть объективным признаком возможных состояний является некая измеренная на опыте случайная величина X. Будем полагать, что закон распределения этой случайной величины нам известен. При этом для обоих состояний вид закона один и тот же, но параметры различны.
При этом имеем:
 ;
;
 ,
,
М[x]=mi - математическое ожидание случайной величины X в состоянии wi
 =D[x] - дисперсия случайной величины X
=D[x] - дисперсия случайной величины X
Представим на графике плотности распределения f (x /w1) и f (x /w2).
Определим на этом графике некоторую граничную точку XO, такую, что, если X, измеренный на опыте, меньше XО следовательно преимущественным является состояние w1 и надо принимать решение d1.
Если X 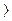 XO то w2 (d2).
XO то w2 (d2).
Однако, как видно из рисунка, при X 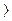 XO существует вероятность пребывания объекта в состоянии w1. Эта вероятность численно равна заштрихованной на рисунке площади:
XO существует вероятность пребывания объекта в состоянии w1. Эта вероятность численно равна заштрихованной на рисунке площади:
P12 = 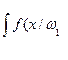 ) dx =
) dx =  ) dx,
) dx,
где: Р12 - вероятность совершить ошибку 1-го рода (отвергаем истину)
С12 - плата за эту ошибку
При X  XO может проявиться с какой-то вероятностью состояние w2
XO может проявиться с какой-то вероятностью состояние w2
То есть аналогично: P21 =  ) dx =
) dx =  ) dx
) dx
Где, Р21 - ошибка 2-го рода (ложь принимаем за истину)
С21 - цена ошибки 2 - го рода.
В остальных случаях решения будут правильными и цена их будет С11 и С22 (премии). Обычно С11 и С22 принимаются равными нулю.
Их вероятности:
P11 =  ) dx;
) dx;
P22 =  ) dx.
) dx.
Таким образом, по итогам испытания могут быть приняты как правильные, так и неправильные решения, то есть функция потерь может быть представлена так называемой платежной матрицей:

Каждый элемент этой матрицы может проявиться с определенной вероятностью, то есть платежной матрице можно поставить в соответствии матрицу вероятностей

На самом деле это матрица условных вероятностей.
Для перехода к матрице безусловных вероятностей, необходимо знать с какой вероятностью проявляются сами состояния w1 и w2

Любой этот элемент представляет собой вероятность одновременного свершения двух событий. Можно без труда определить математическое ожидание некоторой случайной величины С - платы за принятое решение.
М  = R - средний риск
= R - средний риск
Зная матрицу С и Р можно легко записать значение для R:
R = C11P1P11 + C12P1P12 + C21P2P21 + C22P2P22 (1)
Зависимость (1) есть функция XO. Мы заинтересованы в том, чтобы
R  min (2)
min (2)
Зависимость (2) называется байесовский риск, а правило принятия решений на основе (2) называется байесовским принципом решений на множестве D.
Представив (1) в развернутом виде можно найти dR/dXO и тогда получим:
dR/dXO = C11P1f (XO/d1 ) - C12P1f(XO/d1 ) + C21P2f(XO/d2) - C22P2f(XO/d2 ) = 0
f (XO/d1) (C12P1 - C11P1) = f (XO/d2) (C22P2 - P21P2)
f (XO/d1) / f (XO/d2 ) = (C22 - C21) P2 / (C11 - C12) P1 = 
Если по итогам испытаний будет получено такое значение признака, то есть величина х, при котором отношение f (x/d1) / f (x/d2) 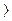
 , то X
, то X  XO и нужно принимать решение d1, а иначе - d2.
XO и нужно принимать решение d1, а иначе - d2.
Частные случаи:
1. На практике бывают случаи когда элементы платежной матрицы неизвестны и их полагают C12 = C21 = 1, тогда  = Р2 / P1, если С11 = С22 = 0. Это, так называемое, условие идеального наблюдения (условие Зигерта - Котельникова).
= Р2 / P1, если С11 = С22 = 0. Это, так называемое, условие идеального наблюдения (условие Зигерта - Котельникова).
2. Априорные вероятности равны друг другу следовательно  = 1 - случай max правдоподобия. Если f (x/d1 )
= 1 - случай max правдоподобия. Если f (x/d1 ) 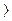 f (x/d2) следовательно нужно принимать решение d1.
f (x/d2) следовательно нужно принимать решение d1.
Минимаксный принцип.
Пусть исследуемый объект может прибывать в двух состояниях w1 и w2, и мы можем принимать решения d1 и d2;
f (x/d1), f (x/d2) – заданы,
C11=C22=0; C12, C21 - заданы.
P1 и P2 - неизвестны.
P2 = 1- P1 (то есть выполняется условие нормировки)
Запишем значение риска:
R = C12P1P12 + C21(1-P1)P21 - риск от P1 зависит линейно.
Не имея возможности влиять на P1, постараемся влиять на 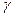 (
( R
R  ).
).
Для того, чтобы оценить возможность влиять на  раскроем выражение для риска:
раскроем выражение для риска:
R = C12P1  ) dx + C21(1-P1)
) dx + C21(1-P1)  ) dx (3)
) dx (3)
 R /
R /  P1 = C12
P1 = C12  )dx - C21
)dx - C21  ) dx =
) dx =  (X0 ) (4)
(X0 ) (4)
С другой стороны  R /
R /  P1 = tg
P1 = tg 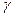
 изменяя значение X0 можно влиять на угол
изменяя значение X0 можно влиять на угол 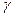 . Допустим
. Допустим  (X0) = 0 и найдем решение этого уравнения:
(X0) = 0 и найдем решение этого уравнения:
Для окончательного решения задачи нужно найти связь между X0 и P1.
 R /
R /  X0 = -C12P1f (X0/d1) + C21 (1-P1)f (X0/d2) = 0 (5)
X0 = -C12P1f (X0/d1) + C21 (1-P1)f (X0/d2) = 0 (5)
Если в уравнении (5) подставить X0, то равенство нулю может быть достигнуто только за счет определенного значения P1.
P1* = P1|Xo = Xo*
P1* = C21 / C21 + C12 (f (Xo*/d1) / f (XO/d2)) (6)
R (X*,P1*) = min max R
xo  {xo} p1
{xo} p1  [a,b]
[a,b]
Теперь можно рассчитать величину:
 = C21 / C12
= C21 / C12  P2 / P1
P2 / P1 
 = C21 / C12
= C21 / C12  1-P1* / P1*
1-P1* / P1*
Если  известно, то вступает в действие принцип Байеса
известно, то вступает в действие принцип Байеса
min max R = C12P1*  )dx + C21 (1-P1* )
)dx + C21 (1-P1* )  2) dx
2) dx
Рекомендации по выполнению работы.
Исходные данные:
Пусть f(x/d) является плотностью нормального распределения с параметрами (например):
_
x1 - 5 г (5 г железа на I тонну масла),
S1 - 2 г,
_
x2 - 12 г,
S2 - 3 г,
Кроме того, на основе анализа статистических данных установлено, что вероятность исправного состояния гидроцилиндра P1= 0,9, т.е. P2= 1- P1= 0,1.
Примем также, что:
C11= C22= 0,
C12= 1,
C21= 20,
т.е. цена ошибки второго рода (цена пропуска дефекта) в 20 раз больше цены ошибки 1-го рода (цены ложной тревоги).
При этих исходных данных необходимо:
1. Определить параметры нормального распределения (оценку математического ожидания x и среднеквадратичного отклонения S для выборок, соответствующих исправному и неисправному состояниям гидроцилиндров):
_
x1, S1,
_
x2, S2,
по формулам:



Примечание: Эти параметры проще рассчитать, скопировав свой вариант в EXEL и воспользовавшись стандартными функциями «СРЗНАЧ» и «ДИСП» для своих выборок. Среднеквадратичное отклонение S получаем, извлекая корень из дисперсии (функция «КОРЕНЬ»).
Ввести полученные данные в соответствующие поля программы «tes_lab1».

Рис.2.
2. Определить (нажав кнопку «РАСЧЕТ») граничное значение x0 и величину риска, используя байесовский принцип и метод минимакса.
3. Изменяя значение цены ошибки второго рода C21, исследовать влияние C21 на x0., рассчитанное по байесовскому принципу и методу минимакса. Построить и проанализировать графики зависимости x0=f(C21). Сделать выводы.
4. Изменяя значение вероятности исправного состояния гидроцилиндра P1, исследовать влияние P1 на x0., рассчитанное по байесовскому принципу и методу минимакса. Построить и проанализировать графики зависимости x0=f(P1). Сделать выводы.
Варианты заданий
| №
| Состояние
| результаты измерений содержания
| | | | |
| вар.
| гидроцилиндра
| железа в масле гидроцилиндра г/т
| | | | |
|
| исправный
| 3,59
| 7,06
| 5,49
| 8,29
| 5,03
| 4,74
| 7,41
| 3,64
| 3,87
|
| | неисправный
| 12,77
| 12,87
| 14,84
| 13,48
| 7,03
| 10,34
| 8,32
| 12,96
| 11,06
|
|
| исправный
| 6,91
| 7,10
| 7,53
| 3,62
| 7,51
| 3,49
| 4,04
| 5,20
| 2,81
|
| | неисправный
| 8,67
| 8,86
| 17,07
| 11,39
| 16,42
| 13,34
| 8,92
| 14,79
| 11,26
|
|
| исправный
| 2,23
| 6,01
| 8,31
| 5,13
| 3,17
| 7,17
| 3,03
| 7,56
| 3,18
|
| | неисправный
| 11,55
| 14,88
| 15,22
| 9,65
| 13,79
| 12,80
| 11,53
| 15,08
| 16,89
|
|
| исправный
| 2,82
| 7,23
| 4,50
| 4,83
| 7,64
| 2,00
| 4,37
| 1,93
| 4,33
|
| | неисправный
| 9,87
| 16,93
| 9,66
| 16,16
| 7,23
| 10,10
| 14,91
| 10,16
| 10,24
|
|
| исправный
| 4,41
| 6,84
| 6,92
| 6,72
| 4,07
| 3,22
| 5,83
| 7,19
| 7,46
|
| | неисправный
| 10,06
| 12,28
| 14,70
| 6,69
| 8,48
| 8,70
| 10,93
| 13,85
| 10,72
|
|
| исправный
| 6,65
| 4,95
| 2,48
| 8,36
| 8,12
| 1,98
| 7,73
| 2,17
| 7,36
|
| | неисправный
| 11,70
| 12,12
| 14,94
| 6,82
| 12,04
| 12,77
| 12,62
| 10,89
| 10,11
|
|
| исправный
| 2,31
| 1,87
| 2,82
| 1,89
| 2,39
| 6,77
| 5,18
| 6,51
| 5,22
|
| | неисправный
| 16,24
| 10,22
| 15,26
| 14,16
| 15,39
| 11,93
| 16,93
| 8,55
| 11,19
|
|
| исправный
| 6,12
| 5,11
| 6,59
| 5,31
| 7,80
| 7,03
| 5,55
| 4,86
| 6,72
|
| | неисправный
| 11,90
| 9,33
| 12,37
| 7,84
| 7,13
| 13,81
| 12,96
| 7,24
| 14,85
|
|
| исправный
| 3,13
| 1,74
| 7,98
| 7,90
| 4,53
| 4,88
| 2,44
| 6,98
| 4,27
|
| | неисправный
| 17,10
| 7,95
| 9,61
| 12,51
| 9,33
| 12,78
| 8,77
| 7,53
| 13,08
|
|
| исправный
| 5,13
| 3,82
| 7,04
| 6,67
| 3,82
| 5,76
| 4,03
| 6,22
| 2,29
|
| | неисправный
| 11,45
| 13,87
| 12,24
| 8,72
| 16,79
| 11,71
| 10,96
| 15,36
| 9,72
|
|
| исправный
| 4,62
| 5,87
| 2,23
| 6,19
| 2,46
| 2,61
| 6,00
| 2,75
| 7,52
|
| | неисправный
| 6,91
| 16,79
| 10,16
| 17,15
| 7,33
| 7,38
| 9,37
| 16,55
| 16,98
|
|
| исправный
| 2,22
| 7,35
| 4,07
| 3,46
| 2,16
| 4,44
| 8,29
| 3,36
| 2,74
|
| | неисправный
| 6,99
| 10,20
| 8,86
| 9,56
| 10,97
| 9,90
| 12,69
| 9,95
| 10,61
|
|
| исправный
| 5,64
| 5,73
| 6,16
| 4,57
| 8,17
| 6,71
| 2,09
| 1,90
| 5,99
|
| | неисправный
| 12,10
| 15,68
| 12,61
| 14,27
| 15,33
| 13,01
| 16,37
| 11,80
| 16,71
|
|
| исправный
| 2,20
| 5,01
| 7,64
| 8,20
| 3,59
| 8,11
| 1,74
| 4,94
| 6,42
|
| | неисправный
| 14,10
| 16,08
| 15,83
| 8,04
| 17,05
| 15,44
| 8,81
| 8,97
| 17,17
|
|
| исправный
| 6,83
| 2,01
| 7,13
| 7,54
| 7,19
| 7,44
| 5,78
| 7,25
| 3,67
|
| | неисправный
| 13,75
| 8,50
| 15,59
| 12,08
| 8,18
| 10,39
| 10,52
| 9,46
| 6,82
|
|
| исправный
| 7,69
| 6,18
| 7,46
| 6,74
| 7,87
| 4,51
| 3,15
| 2,34
| 2,43
|
| | неисправный
| 8,23
| 11,15
| 15,09
| 11,33
| 17,49
| 7,25
| 13,95
| 13,18
| 15,13
|
|
| исправный
| 6,81
| 1,67
| 1,80
| 5,66
| 6,14
| 3,97
| 3,38
| 8,22
| 5,94
|
| | неисправный
| 16,68
| 8,58
| 16,73
| 12,84
| 9,84
| 6,70
| 7,31
| 9,58
| 7,09
|
|
| исправный
| 3,11
| 4,96
| 6,30
| 3,23
| 2,52
| 6,97
| 3,90
| 5,34
| 4,35
|
| | неисправный
| 10,86
| 10,96
| 10,03
| 12,94
| 12,24
| 13,12
| 8,98
| 16,58
| 11,92
|
|
| исправный
| 2,16
| 3,10
| 3,10
| 7,30
| 7,41
| 6,67
| 5,95
| 6,66
| 4,56
|
| | неисправный
| 8,88
| 16,85
| 6,98
| 9,21
| 16,41
| 9,38
| 10,77
| 6,63
| 8,79
|
|
| исправный
| 2,00
| 3,08
| 4,29
| 4,36
| 7,13
| 7,77
| 8,27
| 7,46
| 7,69
|
| | неисправный
| 8,74
| 7,94
| 7,01
| 9,24
| 12,06
| 13,86
| 14,76
| 7,48
| 16,13
|
|
| исправный
| 4,64
| 4,59
| 3,19
| 4,48
| 3,11
| 3,30
| 4,38
| 3,19
| 2,46
|
| | неисправный
| 12,57
| 12,70
| 16,43
| 15,98
| 16,15
| 14,66
| 12,81
| 11,41
| 13,52
|
|
| исправный
| 5,34
| 2,41
| 2,00
| 4,69
| 3,29
| 7,08
| 7,00
| 7,97
| 4,87
|
| | неисправный
| 7,25
| 12,25
| 15,16
| 11,27
| 6,91
| 14,63
| 13,33
| 8,96
| 9,03
|
|
| исправный
| 7,00
| 4,32
| 7,51
| 5,65
| 2,03
| 4,18
| 5,12
| 4,97
| 8,35
|
| | неисправный
| 17,17
| 16,32
| 6,80
| 8,67
| 11,33
| 8,22
| 16,23
| 13,22
| 13,07
|
|
| исправный
| 2,07
| 5,23
| 2,57
| 5,02
| 7,69
| 3,10
| 5,98
| 8,32
| 2,31
|
| | неисправный
| 8,82
| 11,92
| 17,28
| 15,38
| 8,28
| 16,60
| 7,85
| 7,64
| 10,14
|
|
| исправный
| 3,69
| 4,82
| 5,35
| 8,20
| 6,82
| 1,80
| 4,53
| 4,91
| 3,30
|
| | неисправный
| 10,59
| 8,27
| 9,33
| 12,76
| 12,90
| 11,99
| 16,02
| 7,74
| 10,33
|
|
| исправный
| 3,00
| 8,22
| 4,62
| 5,40
| 3,60
| 4,35
| 2,18
| 4,47
| 3,70
|
| | неисправный
| 15,28
| 9,16
| 10,91
| 12,33
| 13,40
| 10,41
| 8,99
| 13,97
| 13,84
|
Пример оформления отчета по лабораторной работе №1
Лабораторная работа - 1
Лабораторная работа № 2.
Постановка задачи.
Рассматривается стрельба артиллерийским бронебойным снарядом по бронеплите. В качестве показателя эффективности действия БП-ов используется величина V псп– скорость предела сквозного пробития. Показатель зависит от двух групп факторов (рис.1): конструктивных характеристик БП и их технологических отклонений. Из числа конструктивных характеристик учитываются:
d + Dd - калибр [м];
q + D q - масса [кг];
h гч + D h гч- высота головной части [м];
b + D b - толщина преграды [м];
s т + Ds т- предел текучести материала преграды [Па];
r + Dr - плотность материала преграды [кг/м3];
d т + D d т- диаметр притупления головной части [м].
Рекомендуемые примерные отклонения параметров + D:
калибр - до 0.5%;
масса - (2/3)%;
высота головной части - до 5%;
толщина преграды - до 0.5%;
предел текучести мат. преграды - до 3%;
плотность мат. преграды - до 1%;
диаметр притупления головной части до 1%.
500 количество опытов
10 количество pазpядов (выбирается в зависимости от количества опытов);
Требуется, используя метод вычислительного эксперимента, рассчитать статистические характеристики распределения значений скорости предела сквозного пробития преграды, установить вид и параметры закона распределения. Сделать выводы по результатам исследования.
Рис.1 Расчетная схема.
Описание метода.
Метод исследования: метод статистических испытаний заключается в воспроизведении исследуемого физического процесса при помощи вероятностной математической модели и вычи
Статистической гипотезой (СГ) называется любое предположительное суждение о вероятностных характеристиках случайных величин.
Различают два вида статистических гипотез: о законах распределения и о числовых характеристиках. Например, предположение о том, что исследуемая случайная величина подчиняется нормальному распределению, является статистической гипотезой первого вида.
Любая СГ может быть принята или отклонена только после проверки ее соответствия опытным данным. Сущность проверки заключается в том, чтобы установить, можно ли расхождение между гипотезой и опытными данными (а такое расхождение всегда будет иметь место) отнести на счет случайной погрешности.
Очевидно, что положительный ответ на данный вопрос будет свидетельствовать в пользу выдвинутой гипотезы. В противном случае придется заключить, что гипотеза не согласуется с опытными данными.
Правило, по которому принимается или отклоняется СГ, называется критерием проверки гипотез. Критерии формируются на основе статистик.
Характерной для практики задачей является аппроксимация эмпирических распределений некоторыми теоретическими, свойства которых известны.

где  соответственно эмпирическое и теоретическое распределения. Из числа непрерывных распределений важную роль играет нормальное распределение, которое является основным для случайных величин, изменяющихся на бесконечном интервале, когда
соответственно эмпирическое и теоретическое распределения. Из числа непрерывных распределений важную роль играет нормальное распределение, которое является основным для случайных величин, изменяющихся на бесконечном интервале, когда  и отражает процессы, происходящие под воздействием большого числа факторов;
и отражает процессы, происходящие под воздействием большого числа факторов;
Следует, однако, помнить, что нередко одной и той же гипотезе Но, как показывает практика, может удовлетворять несколько теоретических распределений. Принятие гипотезы Но означает лишь то, что выбранное распределение не противоречит опытным данным. Продолжение испытаний может привести к опровержению сделанного заключения, причем для опровержения достаточно небольшого числа противоречащих основной гипотезе результатов (иногда единичного), в то время как для ее подтверждения необходим большой объем испытаний. Тем самым реализуется принцип асимметрии принятия решений.
Вторая особенность заключается в том, что критическая область всегда является правосторонней вследствие специфики применяемых статистических критериев. При этом, поскольку проверка гипотез о законах распределения всегда проводится при сравнительно большом числе опытных данных, то уровень значимости a = 0,1...0,3 до 0,4.
Наконец, выбор статистического критерия, как и выбор класса теоретических распределений не является формализованным и осуществляется на основе оценки свойств выборочной совокупности (прежде всего ее объема) и свойств самих критериев.
Рассмотрим свойства наиболее распространенных статистических критериев. Применительно к гипотезе первого типа, т.е. к гипотезе Но:  , такими критериями являются: критерий
, такими критериями являются: критерий  (Пирсона), критерий l (Колмогорова) и критерий w2 (Мазеса - Крамера - Смирнова).
(Пирсона), критерий l (Колмогорова) и критерий w2 (Мазеса - Крамера - Смирнова).
Статистика критерия Пирсона имеет вид:

где i - порядковый номер интервала гистограммы;
k -число интервалов гистограммы,
mi - количество попаданий случайной величины в i -ый интервал,
n - общее число опытов
 -эмпирическая вероятность попадания случайной величины в i -ый интервал
-эмпирическая вероятность попадания случайной величины в i -ый интервал
pi=Fi(x) - теоретическая вероятность попадания случайной величины в i -ый интервал
Как видно, в качестве меры расхождения между эмпирическим  и теоретическим F(x) законами распределения критерий Пирсона использует относительный квадрат отклонений по всем интервалам гистограммы
и теоретическим F(x) законами распределения критерий Пирсона использует относительный квадрат отклонений по всем интервалам гистограммы
Критическое значение  табулировано и находится по уровню значимости a и числу степеней свободы n=k-i-1, где i - количество связей, определенно числом оценок параметров, вычисленных по данным выборки. Так, для нормального распределения i=2, если оба параметра x и Sx вычислены по результатам испытаний.
табулировано и находится по уровню значимости a и числу степеней свободы n=k-i-1, где i - количество связей, определенно числом оценок параметров, вычисленных по данным выборки. Так, для нормального распределения i=2, если оба параметра x и Sx вычислены по результатам испытаний.
Гипотеза Но принимается, если расчетное значение  .
.
Критерий  используется при
используется при  (по крайней мере
(по крайней мере  ). Существенным его недостатком является произвол в разбиении области значений случайной величины на интервалах, что влияет на объективность вывода. Для того, чтобы уменьшить влияние этого недостатка на окончательное решение, целесообразно руководствоваться следующим положением: при слишком большом числе интервалов картина распределения исследования случайной величины искажается случайными зигзагами частот, слишком малочисленных при узких интервалах; при слишком малом числе интервалов сглаживаются и затушевываются характерные особенности распределения. Поэтому необходимы многовариантные расчеты с разным числом интервалов. В общем случае число k зависит от объема выборки n. Приведем некоторые рекомендации по его выбору:
). Существенным его недостатком является произвол в разбиении области значений случайной величины на интервалах, что влияет на объективность вывода. Для того, чтобы уменьшить влияние этого недостатка на окончательное решение, целесообразно руководствоваться следующим положением: при слишком большом числе интервалов картина распределения исследования случайной величины искажается случайными зигзагами частот, слишком малочисленных при узких интервалах; при слишком малом числе интервалов сглаживаются и затушевываются характерные особенности распределения. Поэтому необходимы многовариантные расчеты с разным числом интервалов. В общем случае число k зависит от объема выборки n. Приведем некоторые рекомендации по его выбору:
Если интервалы одинаковой длины, то для ее определения используют величину размаха выборки R=Xmax-Xmin, где Xmax, Xmin - минимальное и максимальное значения выборки. В этом случае длина интервала определяется формулой:

Границы отделенных интервалов определяются соотношениями:
1-й интервал: xmin-D; xmin-D+d,
2-й интервал: xmin-D+d; xmin-D+2d,
…………………….
j-й интервал: xmin-D+(i-1)d; xmin-D+id,
……………………
k-й интервал: xmin-D+(k-1)d; xmin-D+kd,
где D=0,01d.
После выбора интервалов подсчитывают mi - число наблюдений, попавших в интервал [di],  , т.е. в интервал включаются и те наблюдения, которые приходятся на левую границу интервала.
, т.е. в интервал включаются и те наблюдения, которые приходятся на левую границу интервала.
Рекомендации по выполнению работы.
Цель работы: Ознакомление с методом статистических испытаний на примере определения гарантированной скорости сквозного пробития бронированной преграды, путем моделирования бронепробития.
Задачи работы:
1. изучить сущность метода статистических испытаний;
2. изучить методы проверки согласия статистического и теоретического законов распределения;
3. изучить стохастическую модель бронепробития;
4. произвести обработку и анализ результатов расчета.
Теоретический материал
Метод Монте-Карло: Метод статистических испытаний заключается в воспроизведении исследуемого физического процесса при помощи вероятностной математической модели и вычислении характеристик этого процесса. Таким образом, метод Монте-Карло - это численный метод решения математической задачи при помощи моделирования случайных величин. Метод основан на многократном проведении испытаний построенной модели с последующей статистической обработкой для определения характеристик рассматриваемого процесса в виде статистических оценок его параметров.
Этот метод целесообразно применять при исследовании систем, функционирование которых определяется многими вероятностными параметрами элементарных явлений; когда построение чисто аналитической вероятностной модели такой системы затруднено. Он базируется на использовании случайных чисел - возможных значений некоторой случайной величины с заданным законом распределения.
Стохастическая модель: Все наблюдаемые процессы, характеризующие физические явления, можно классифицировать в общем виде как детерминированные и недетерминированные. К детерминированным относятся процессы, которые могут быть описаны точными математическими соотношениями. Математические модели движения снаряда в канале ствола орудия, в воздухе после вылета из канала ствола, являются детерминированными. Однако в действительности ни один реальный физический процесс нельзя считать строго детерминированным, поскольку всегда существует возможность того, что какое-то непредвиденное событие изменит течение процесса таким образом, что полученные результа



 d1,
d1,
 ;
; ,
, =D[x] - дисперсия случайной величины X
=D[x] - дисперсия случайной величины X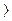 XO то w2 (d2).
XO то w2 (d2).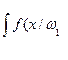 ) dx =
) dx =  ) dx,
) dx, XO может проявиться с какой-то вероятностью состояние w2
XO может проявиться с какой-то вероятностью состояние w2 ) dx =
) dx =  ) dx.
) dx.


 = R - средний риск
= R - средний риск min (2)
min (2)
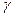 (
( R
R  ).
). раскроем выражение для риска:
раскроем выражение для риска: R /
R /  (X0 ) (4)
(X0 ) (4) изменяя значение X0 можно влиять на угол
изменяя значение X0 можно влиять на угол  {xo} p1
{xo} p1  P2 / P1
P2 / P1  2) dx
2) dx





 соответственно эмпирическое и теоретическое распределения. Из числа непрерывных распределений важную роль играет нормальное распределение, которое является основным для случайных величин, изменяющихся на бесконечном интервале, когда
соответственно эмпирическое и теоретическое распределения. Из числа непрерывных распределений важную роль играет нормальное распределение, которое является основным для случайных величин, изменяющихся на бесконечном интервале, когда  и отражает процессы, происходящие под воздействием большого числа факторов;
и отражает процессы, происходящие под воздействием большого числа факторов; , такими критериями являются: критерий
, такими критериями являются: критерий  (Пирсона), критерий l (Колмогорова) и критерий w2 (Мазеса - Крамера - Смирнова).
(Пирсона), критерий l (Колмогорова) и критерий w2 (Мазеса - Крамера - Смирнова).
 -эмпирическая вероятность попадания случайной величины в i -ый интервал
-эмпирическая вероятность попадания случайной величины в i -ый интервал и теоретическим F(x) законами распределения критерий Пирсона использует относительный квадрат отклонений по всем интервалам гистограммы
и теоретическим F(x) законами распределения критерий Пирсона использует относительный квадрат отклонений по всем интервалам гистограммы табулировано и находится по уровню значимости a и числу степеней свободы n=k-i-1, где i - количество связей, определенно числом оценок параметров, вычисленных по данным выборки. Так, для нормального распределения i=2, если оба параметра x и Sx вычислены по результатам испытаний.
табулировано и находится по уровню значимости a и числу степеней свободы n=k-i-1, где i - количество связей, определенно числом оценок параметров, вычисленных по данным выборки. Так, для нормального распределения i=2, если оба параметра x и Sx вычислены по результатам испытаний. .
. (по крайней мере
(по крайней мере  ). Существенным его недостатком является произвол в разбиении области значений случайной величины на интервалах, что влияет на объективность вывода. Для того, чтобы уменьшить влияние этого недостатка на окончательное решение, целесообразно руководствоваться следующим положением: при слишком большом числе интервалов картина распределения исследования случайной величины искажается случайными зигзагами частот, слишком малочисленных при узких интервалах; при слишком малом числе интервалов сглаживаются и затушевываются характерные особенности распределения. Поэтому необходимы многовариантные расчеты с разным числом интервалов. В общем случае число k зависит от объема выборки n. Приведем некоторые рекомендации по его выбору:
). Существенным его недостатком является произвол в разбиении области значений случайной величины на интервалах, что влияет на объективность вывода. Для того, чтобы уменьшить влияние этого недостатка на окончательное решение, целесообразно руководствоваться следующим положением: при слишком большом числе интервалов картина распределения исследования случайной величины искажается случайными зигзагами частот, слишком малочисленных при узких интервалах; при слишком малом числе интервалов сглаживаются и затушевываются характерные особенности распределения. Поэтому необходимы многовариантные расчеты с разным числом интервалов. В общем случае число k зависит от объема выборки n. Приведем некоторые рекомендации по его выбору:
 , т.е. в интервал включаются и те наблюдения, которые приходятся на левую границу интервала.
, т.е. в интервал включаются и те наблюдения, которые приходятся на левую границу интервала.

