

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует...
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Интересное:
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Горизонталь плоскости.
Это прямая, принадлежащая плоскости, и параллельная горизонтальной плоскости проекций (рис. 17а,б)).Построение горизонтали начинают с фронтальной проекции, так как она всегда параллельна оси х12. Все горизонтали плоскости параллельны между собой.
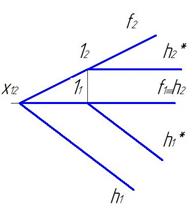
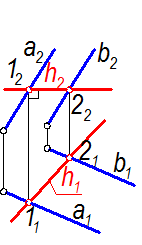
а) б)
Рис.17
Фронталь плоскости.
Это прямая, принадлежащая плоскости, и параллельная фронтальной плоскости проекций (рис. 18а, б). Построение фронтали всегда начинают с горизонтальной проекции, так как она всегда параллельна оси х12. Все фронтали плоскости параллельны между собой.
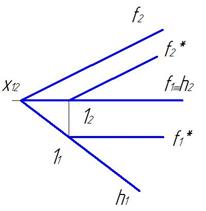
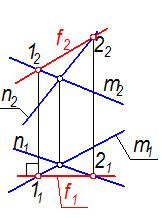
а) б)
Рис. 18
Параллельность прямой и плоскости
Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, лежащей в этой плоскости.
Проведем в плоскости, заданной двумя пересекающимися прямыми а и в, любую прямую n. Затем через точку К построим прямую m║ n (рис. 19). У параллельных прямых параллельны одноименные проекции.
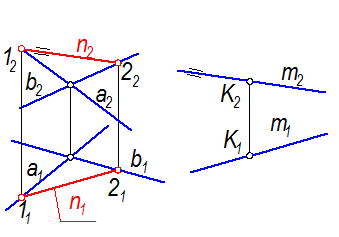
Рис. 19
Теорема о проекциях прямого угла
Помимо позиционных задач, рассмотренных в предыдущих параграфах, в практике приходится решать задачи на определение расстояний, углов и истинных величин плоских фигур. Такие задачи называются метрическими задачами. При их решении необходимо знать условие перпендикулярности прямых и плоскостей. Для этого надо выяснить свойство ортогональной проекции прямого угла.
Если одна сторона прямого угла параллельна плоскости проекций, то на эту плоскость проекций прямой угол проецируется без искажения (рис. 20).
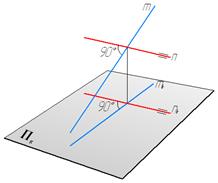
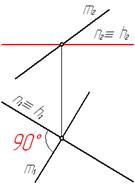
Рис. 20
На рис. 21 показаны скрещивающиеся прямые, перпендикулярные друг другу.
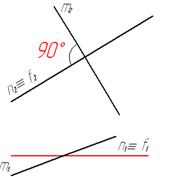
Рис. 21
Перпендикулярность прямой и плоскости
Из геометрии известно, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости (рис. 22).
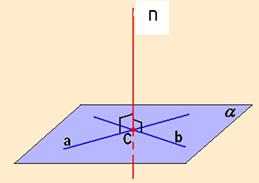
Рис. 22
Если прямые а и в будут прямыми общего положения, то прямой угол к ним ни на одной плоскости проекций не спроецируется в натуральную величину. Согласно теореме о проецировании прямого угла, прямой угол спроецируется в натуральную величину на плоскость проекций, если одна сторона прямого угла будет параллельной этой плоскости проекций. Поэтому, в качестве прямых надо взять горизонталь h и фронталь f. Тогда прямой угол между перпендикуляром n и h спроецируется в натуральную величину на П1, а прямой угол между n и f - на П2. На рис. 23 в точке К, принадлежащей плоскости α(а║b), построен перпендикуляр n к плоскости.
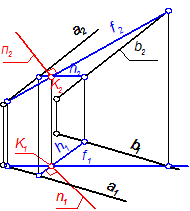
Рис. 23
Применение дополнительного ортогонального проецирования
Для решения задач
Пример. Найти длину отрезка АВ.
Чтобы найти длину отрезка занимающего в пространстве общее положение относительно плоскостей П1 и П2, надо построить дополнительную ортогональную проекцию отрезка АВ на плоскость П4 ему параллельную (П4║АВ) и П4^П1 (рис. 24).
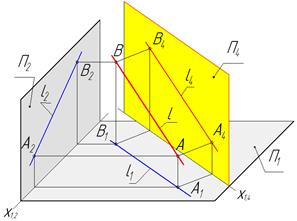
Рис.24
Поэтапное решение задачи на эпюре показано на рис. 25
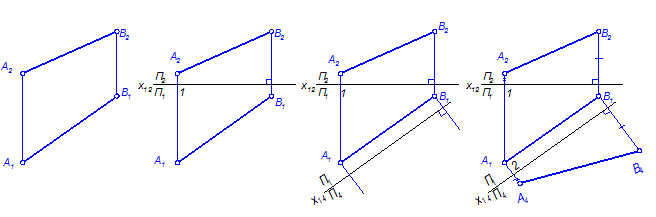
Рис. 25
Пример 2. Построить дополнительную ортогональную проекцию плоскости общего положения α(ΔАВС) на плоскости П4,перпендикулярной к плоскости α и к плоскости П1.
Из геометрии известно, что две плоскости взаимноперпендикулярны, если одна из них содержит прямую, перпендикулярную другой плоскости. В данном примере перпендикуляром к плоскости П4 является горизонталь h (рис. 26).
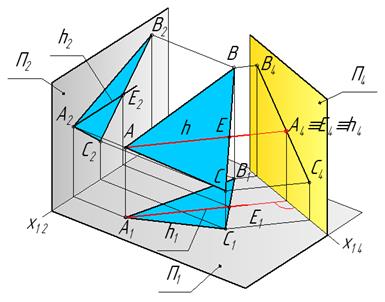
Рис. 26
Исходя из этого, ось х14 проведена перпендикулярно горизонтальной проекции h1 горизонтали h плоскости ΔАВС (рис. 27).По отношению к плоскости П4 плоскость ΔАВС является проецирующей и изображается на ней в виде прямой А4 В4 С4.
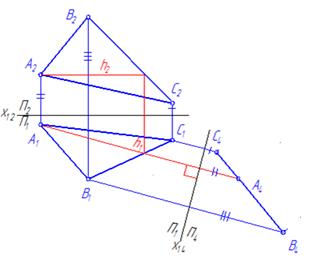
Рис. 27
Пример3. Построить дополнительную ортогональную проекцию прямой общего на плоскость ей перпендикулярную.
Для этого надо сначала построить дополнительную ортогональную проекцию прямой АВ на плоскость ей параллельную (П4║АВ) и П4┴П1.Ось х14 построена параллельно А1 В1. Затем построить дополнительную ортогональную проекцию прямой АВ на плоскость П5 ей перпендикулярную(П5┴ АВ) и П5┴ П4 (рис. 28).Ось х45 построена перпендикулярно А4 В4..На плоскости П5 прямая будет точкой.
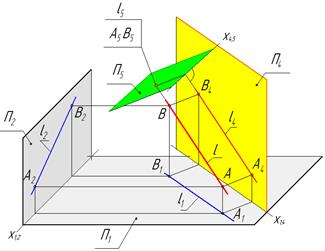
Рис. 28
Рещение задачи на эпюре показано на рис. 29
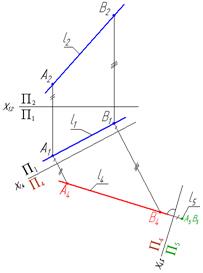
Рис. 29
Пример 4.Определить размеры треугольника АВС.
Чтобы найти величину ΔАВС,являющегося плоскостью общего положения,надо построить его дополнительную ортогональную проекцию на плоскость ему параллельную. Для этого надо сначала построить дополнительную ортогональную проекцию плоскости общего положения α(ΔАВС) на плоскости П4,перпендикулярной к плоскости α(ΔАВС) и к плоскости П1 (см.пример2).А затем построить его дополнительную ортогональную проекцию на плоскость П5 ему параллельную(П5║ ΔАВС) и П5┴ П4 (рис.30а).Решение задачи на эпюре показано на рис.30б.
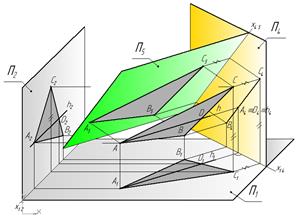
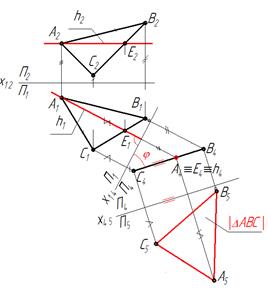
Рис. 30а Рис.30б
|
|
|

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...
© cyberpedia.su 2017-2026 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!