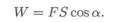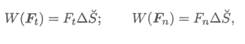Метод кинетостатики

108 Лекция 14

 Тема 1.14. Работа и мощность 109
Тема 1.14. Работа и мощность 109
ЛЕКЦИЯ 15
Тема 1.14. Работа и мощность
Иметь представление о работе силы при прямолинейном и криволинейном перемещениях, о мощности полезной и затраченной, о коэффициенте полезного действия.
Знать зависимости для определения силы трения, формулы для расчета работы и мощности при поступательном и вращательном движениях.
Уметь рассчитывать работу и мощность с учетом потерь на трение и сил инерции.
Работа
Для характеристики действия силы на некотором перемещении точки ее приложения вводят понятие «работа силы».
Работа служит мерой действия силы, работа — скалярная величина.
Работа постоянной силы на прямолинейном пути
Работа силы в общем случае численно равна произведению модуля силы на длину пройденного пути и на косинус угла между направлением силы и направлением перемещения (рис. 15.1): 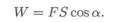

Единицы измерения работы: 1Дж (джоуль)= 1Н ∙ м; 1кДж (килоджоуль) = 103Дж. Рассмотрим частные случаи.
1. Силы, совпадающие с направлением перемещения, называются движущими силами. Направление вектора силы совпадает с направлением перемещения (рис. 15.2).
В этом случае α = 0° (cos α = 1). Тогда W = FS > 0.
2. Силы, перпендикулярные направлению перемещения, работы
не производят (рис. 15.3).
110 Лекция 15

Сила F перпендикулярна направлению перемещения, α = 90° (cos α = 0); W = 0.
2. Силы, направленные в обратную от направления перемещения сторону, называются силами сопротивления (рис. 15.4).

Сила F направлена в обратную от перемещения S сторону.
В этом случае α= 180° (cos α = - 1), следовательно, W = -FS < 0. Движущие силы увеличивают модуль скорости, силы сопротивления уменьшают скорость.
Таким образом, работа может быть положительной и отрицательной в зависимости от направления силы и скорости.
Работа постоянной силы на криволинейном пути
Пусть точка М движется по дуге окружности и сила F составляет некоторый угол α с касательной к окружности (рис. 15.5).

Вектор силы можно разложить на две составляющие:
F = Ft + Fn.
Используя принцип независимости действия сил, определим работу каждой из составляющих силы отдельно:
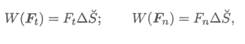
Тема 1.14. Работа и мощность 111

Нормальная составляющая силы F n всегда направлена перпендикулярно перемещению и, следовательно, работы не производит: W( F n) = 0.
При перемещении по дуге обе составляющие силы разворачиваются вместе с точкой М. Таким образом, касательная составляющая силы всегда совпадает по направлению с перемещением.
Будем иметь: W( F t) = Ft φ r.
Касательную силу F t обычно называют окружной силой.
Работа при криволинейном пути — это работа окружной силы:

Произведение окружной силы на радиус называют вращающим моментом:

Работа силы, приложенной к вращающемуся телу, равна произведению вращающего момента на угол поворота:

Работа силы тяжести
Работа силы тяжести зависит только от изменения высоты и равна произведению модуля силы тяжести на вертикальное перемещение точки (рис.15.6): 
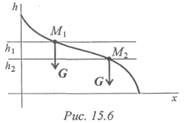
При опускании работа положительна, при подъеме отрицательна.







 Тема 1.14. Работа и мощность 109
Тема 1.14. Работа и мощность 109