 Основные положения. Большинство уравнений статики и гидродинамики получено для идеальной жидкости, отличающихся от реальной жидкости отсутствием сил трения (другими словами – вязкости), ее несжимаемостью и отсутствием температурного расширения. Основными уравнениями гидравлики являются; дифференциальные уравнения Эйлера о движении жидкости, уравнения неразрывности, состояния и сохранения энергии струйки жидкости.
Основные положения. Большинство уравнений статики и гидродинамики получено для идеальной жидкости, отличающихся от реальной жидкости отсутствием сил трения (другими словами – вязкости), ее несжимаемостью и отсутствием температурного расширения. Основными уравнениями гидравлики являются; дифференциальные уравнения Эйлера о движении жидкости, уравнения неразрывности, состояния и сохранения энергии струйки жидкости.




| |
| | | Плоскость сравнения (Z=0)
| |
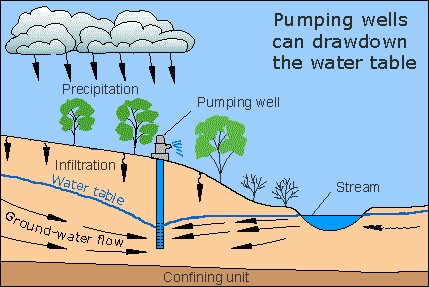
Рисунок – Упрощенная схема движения воды к скважине в зоне насыщения.
Величина гидростатического давления Р в данной точке на глубине h определяется:
Р = Р0 + γ·h, (1)
Где Р0 – гидростатическое давление на свободной поверхности жидкости (атмосферное);
γ·h – избыточное гидростатическое давление столба жидкости высотой h;
γ· - плотность жидкости.
Уравнение неразрывности объема жидкости выражает закон сохранения массы жидкости.
Энергетический потенциал струйки идеальной жидкости определяется уравнением Бернулли (выражает закон сохранения энергии)
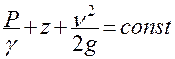 , (2),
, (2),
где  – пьезометрическая высота, вызванная гидростатическим давлением Р жидкости;
– пьезометрическая высота, вызванная гидростатическим давлением Р жидкости;
z – высота рассматриваемой точки относительно плоскости сравнения;
ν – скорость движения жидкости;
g – ускорение силы тяжести;
ν2/2g – высота скоростного напора;
Сумму первых двух членов в (2) называют напором, или пьезометрическим напором
Н = Р/g + z.
При этом (2) преобразуется к виду:
Н + ν2/2g = const (3)
Если бы идеальная жидкость двигалась без трения и с постоянной скоростью, то пьезометрический напор был бы одинаковым во всех точках струйки.

Рисунок - Тубка (струйка) ламинарного течения воды через пористую среду.
Реальная жидкость имеет вязкость и часть энергии теряется на преодоление сил трения, что приводит к падению напора по пути движения жидкости. В гидравлической системе жидкость перемещается за счет разности напоров (от более высокого напора к менее высокому).
Силы инерции (определяются скоростным напором ν2/2g оказывают меньшее влияние на движение свободной гравитационной воды.
Понятие о фильтрации. В горных породах, насыщенных водой она находится в разных состояниях от химически связанной до свободной, которая и заполняет поровое и трещинное пространство. Она и представляет собой основную форму движения подземной воды через сообщающиеся между собой поры, каверны и трещины.
В гидрогеодинамике принято рассматривать не движение воды в каждом отдельном канале, соединяющем трещины, а обобщенно, т.е. через всё поперечное сечение фильтрующей среды в целом.
Скорость фильтрации относится к важнейшей характеристике движеня подземной воды. Она характеризует количество воды, протекающей в единицу времени через единицу площади поперечного сечения пористой среды. Если обозначить объемный расход воды, фильтрующейся в единицу времени через Q, а площадь поперечного сечения фильтрующей среды через F, то скорость фильтрации ν можно записать в виде
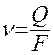 . (4)
. (4)
Размерность скорости фильтрации будет:
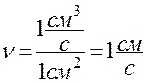 .
.
Используют также и другие единицы измерения: м/сут, см/сут.
Заметим, что скорость фильтрации получена как если бы вода фильтровалась не только через часть поперечного сечения, занимаемую порами, а через всю площадь сечения F (в том числе и занятую скелетом горной породы). C физической точки зрения скорость фильтрации представляет собой фиктивную среднюю скорость, с которой двигалась бы вода, если бы скелет горной породы отсутствовал в поперечном сечении вовсе. При этом всё сечение занимала бы вода.
При рассмотрении задач геогидродинамики (фильтрации подземных вод в пористой среде) подразумевается ламинарное (параллельно-струйное) течение, при котором вода в воображаемых струйках перемещаются параллельно без завихрений.
Турбулентное же движение, в отличие от ламинарного, имеет место при больших скоростях течения, при которых наблюдается вихреобразное течение, перемешивание отдельных струек и пульсация общего потока. В реальных природных условиях в подавляющем большинстве случаев преобладает ламинарное течение. Тубрулентное течение возможно, например, в призабойной зоне скважины при больших скоростях откачки воды, в близи инженерных сооружений.
Линейный закон фильтрации
Линейный закон фильтрации применим к ламинарному движению воды и был установлен экспериментально в 1856 г. Французским гидравликом Ф. Дарси. Проведенный им опыт поясняется на следующем рисунке:

В заполненную песком трубку слева подается вода, проходя фильтруясь через песок она сливается через вторую трубку справа. При этом поддерживаются постоянные уровни Н1 и Н2. Определяли расход воды в зависимости от разности уровней ΔН = Н1 и Н2, длины фильтра ΔL и его площади поперечного сечения F.
Было установлено, что количество воды Q прямо пропорционально F и ΔН и обратно пропорционально длине пути фильтрации ΔL:
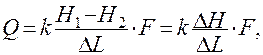 (5)
(5)
Где коэффициент k принято называть коэффициентом фильтрации.
Член 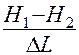 =
=  показывает как изменяется уровень вдоль пути фильтрации и называется напорным или гидравлическим градиентом (уклоном). Его часто обозначают как I. Если разделить обе части (5) на площадь F и с учетом того, что скорость фильтрации
показывает как изменяется уровень вдоль пути фильтрации и называется напорным или гидравлическим градиентом (уклоном). Его часто обозначают как I. Если разделить обе части (5) на площадь F и с учетом того, что скорость фильтрации 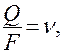 получим для закона Дарси выражение:
получим для закона Дарси выражение:
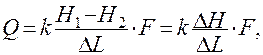 (6)
(6)
Оно представляет собой линейную зависимость скорости фильтрации от гидравлического градиента. Здесь скорость пропорциональна напорному градиенту. В дифференциальной форме линейный закон фильтрации описывается уравнением:
ν=-k  , (7)
, (7)
Минус показывает что скорость течения увеличивается в сторону обратную увеличению напора Н.
Нарушение линейного закона Дарси имеет место при больших скоростях фильтрации, для неньютоновских жидкостей, иногда и для очень малых скоростей. Верхний предел его применимости связан с понятием критической скорости фильтрации. Этот термин введен Павловским Н.Н. и связан с понятием числа Рейнольдса Re, используемого чтобы разграничить ламинарный и турбулентный вид движения воды.
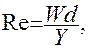 (8)
(8)
где W – средняя скорость движения воды (см/с), d – диаметр трубки с водой (см), а
Y = µ΄/ γ – называют кинематическим коэффициентом вязкости (см2/с), µ΄ - динамический коэффициент вязкости (пуазы – пз), γ – плотность воды (г/см3).
Н.Н. Павловский изменил уравнение (8) введя в него вместо диаметра трубки d и средней скорости движения воды W действующий диаметр зерен dе пористость n и скорость фильтрации ν и получил уравнение:
 (9)
(9)
Было выявлено, что отклонение от линейного закона Дарси происходят при критических значениях Re = 7/5 – 9. Соответствующая им скорость νкр названа критической. Исследованиями показано, что при скоростях воды менее 1000 м/сут применим линейный закон Дарси. При скоростях выше 1000 м/сут используют нелинейный закон Дарси, установленный А.А. Краснопольским:
ν = 
 (10)
(10)
где kк - коэффициент фильтрации Краснопольского. Его формула имеет вид:
 (11)
(11)
Отсюда следует, что для турбулентного движения скорость потока Q пропорциональна гидравлическому градиенту в степени ½. А связь напорного градиента I со скоростью ν записывают и в виде квадратичной зависимости:
 где b – коэффициент пропорциональности (12)
где b – коэффициент пропорциональности (12)





 Основные положения. Большинство уравнений статики и гидродинамики получено для идеальной жидкости, отличающихся от реальной жидкости отсутствием сил трения (другими словами – вязкости), ее несжимаемостью и отсутствием температурного расширения. Основными уравнениями гидравлики являются; дифференциальные уравнения Эйлера о движении жидкости, уравнения неразрывности, состояния и сохранения энергии струйки жидкости.
Основные положения. Большинство уравнений статики и гидродинамики получено для идеальной жидкости, отличающихся от реальной жидкости отсутствием сил трения (другими словами – вязкости), ее несжимаемостью и отсутствием температурного расширения. Основными уравнениями гидравлики являются; дифференциальные уравнения Эйлера о движении жидкости, уравнения неразрывности, состояния и сохранения энергии струйки жидкости.




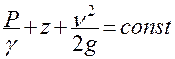 , (2),
, (2), – пьезометрическая высота, вызванная гидростатическим давлением Р жидкости;
– пьезометрическая высота, вызванная гидростатическим давлением Р жидкости;
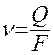 . (4)
. (4)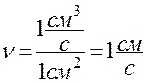 .
.
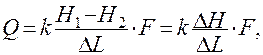 (5)
(5)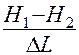 =
=  показывает как изменяется уровень вдоль пути фильтрации и называется напорным или гидравлическим градиентом (уклоном). Его часто обозначают как I. Если разделить обе части (5) на площадь F и с учетом того, что скорость фильтрации
показывает как изменяется уровень вдоль пути фильтрации и называется напорным или гидравлическим градиентом (уклоном). Его часто обозначают как I. Если разделить обе части (5) на площадь F и с учетом того, что скорость фильтрации 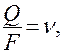 получим для закона Дарси выражение:
получим для закона Дарси выражение: , (7)
, (7)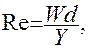 (8)
(8) (9)
(9)
 (10)
(10) (11)
(11) где b – коэффициент пропорциональности (12)
где b – коэффициент пропорциональности (12)


