Общая характеристика методов нулевого порядка

 

В этих методах для определения направления спуска не требуется вычисления производных целевой функции. Направление минимизации в данном случае полностью определяется последовательностью вычисленных значений функции. К ним относятся методы:

- прямого спуска (Хука-Дживса);

- деформируемого многогранника (Нелдера-Мида);

- вращающихся координат (Розенброка);

- параллельных касательных (Пауэлла) [].

9.3 Метод прямого спуска (Хука-Дживса)

Суть этого метода состоит в следующем. Задаются некоторой начальной точкой х[0]. Изменяя компоненты вектора х[0], обследуют окрестности данной точки, в результате чего находят направление, в котором происходит уменьшение минимизируемой функции f(x). В выбранном направлении осуществляют спуск до тех пор, пока значение функции уменьшается. После того, как в данном направлении не удается найти точку с меньшим значением функции, уменьшают величину шага спуска. Если последовательные дробления шага не приводят к уменьшению функции, от выбранного направления спуска отказываются и осуществляют новое обследование окрестности и т.д.

Алгоритм метода прямого спуска.

1.Задаются: значениями координат х_i[0], i = 1,2,3,…,n начальной точки х[0]; вектором изменения координат Δx в процессе обследования окрестности; наименьшим допустимым значением ε компонентов Δx.

2.Полагают, что х[0] является базисной точкой х^Б, вычисляют f(x^Б).

3.Циклически изменяют каждую координату х^Б_i, i=1,2,…,n. базисной точки х^Б на величину Δx_i, т.е. х_i[k] = х^Б_i + Δx_i, х_i[k] = х^Б_i - Δx_i. Вычисляют значение f(x[k]) и сравнивают с f(x^Б). Если f(x[k]) < f(x^Б), то соответствующая координата х_i, i = 1,2,3,…,n, приобретает новое значение, вычисленное по одному из выше приведенных выражений. В противном случае значение этой координаты остается неизменным. Если после изменения последней n-й координаты f(x[k]) < f(x^Б), то переходят к пункту 4., в противном случае к пункту 7.

4.Полагают, что x[k] является новой базисной точкой x^Б и вычисляют значение f(x^Б).

5.Осуществляют спуск из точки x[k]: x[k+1] =2x_i[k]- х^Б_i, i=1,2,…,n, х^Б_i- координаты предыдущей базисной точки. Вычисляют f(x[k+1]).

6. Как в п.3. циклически изменяют каждую координату точки x[k+1], осуществляя сравнение соответствующих значений функции f(x) со значениями f(x[k+1]), полученными в п.5. После изменения последней координаты сравнивают соответствующие значения функции f(x[k+1]) со значением f(x^Б), полученным в п.4. Если f(x[k+1]) < f(x^Б), то переходят к п.4, в противном случае - к п.3. при этом в качестве базисной точки используют последнюю из полученных базисных точек.

7. Сравнивают значения Δx и ε. Если Δx<ε, то вычисления прекращают. В противном случае уменьшают Δx и переходят к п.3.

Достоинством метода является простота его программирования. Он не требует знания целевой функции в явном виде, легко учитывает ограничения на отдельные переменные, а также сложные ограничения на область поиска.

Недостаток – в случае сильно вытянутых, изогнутых или обладающих острыми углами линий уровня целевой функции он может оказаться неспособным обеспечить продвижение к точке минимума.

х₂

с₁

 

 

• с₂

с₃

х΄

 

0 х₁

 

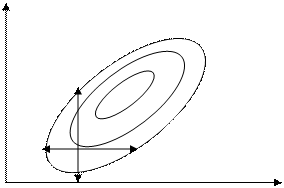
Рисунок 9.5 –Линии уровня и выбор направления движения к минимуму целевой функции

 

Как видно из рисунка, каким бы малым ни брать шаг в направлении х₁ или х₂ из х΄ нельзя получить уменьшения значения целевой функции (с1> >с2>с3).

Поверхностью уровня (на плоскости – линией уровня) является поверхность, получаемая приравниванием выражения функции f(x) некоторой постоянной величине с, т.е. f(x)=с. Во всех точках этой поверхности функция имеет значение с. Изменяя значения постоянной с1, с2, с3, …, сn, получаем ряд поверхностей, геометрически иллюстрирующих характер функции. Как в топографии изобразим рельеф поверхности линиями уровня Ф(х,у) = const.

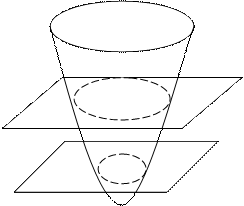
Равноотстоящие плоскости Ф(х,у) = const имеют линии пересечения с поверхностью Ф(х,у,z). Проекции этих линий на плоскости – линии уровня. Направление убывания функции можно показать штрихами.

 

Ф(х,у,z)

 

 

Ф(х,у)

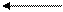Линии уровня

 

 

 

min Ф(х,у,z)

Рисунок 9.6 –Линии уровня для функции Ф(х,у,z)

 

По виду линий уровня можно условно выделить три типа рельефа: котловинный, овражный и неупорядоченный.

у

 

• min

 

. х

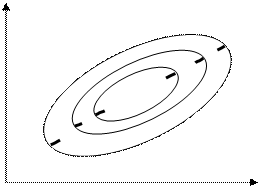
Рисунок 9.7 - Линии уровня для котловинного рельефа

(например, Ф(х,у) = х²/а²+у²/b²)

 

у

 

• min

 

 

х

Рисунок 9.8 - Линии уровня для овражного рельефа

(например, Ф(х,у) = 10(у - sinx)²+0,1x²)

 

Линии уровня для неупорядоченного рельефа, имеют много максимумов, минимумов и седловин.

y

 

• min

 

 

x

 

Рисунок 9.9 - Линии уровня для неупорядоченного рельефа

(например, Ф(х,у) = (1+ sin²x)(1+sin²y))

 

К численным методам решения задач оптимизации первого порядка относятся градиентные методы [].

Градиентные методы, а также численные методы решения задач условной оптимизации будут рассмотрены в курсе «Методы моделирования и оптимизации теплоэнергетических процессов и установок».

Компьютерная реализация методов в Excel описана в [9], [23-26].

Литература: [7], [20].

 

 

Список литературы

 

1. Амосов А.А. Вычислительные методы для инженеров.- М.: МЭИ, 2003. – 596с.

2. Пирумов У.Г. Численные методы. - М.: ДРОФА, 2007.- 221с.

3. Численные методы: Сборник задач /Под ред. У.Г. Пирумова. - М.: ДРОФА, 2007.- 144 с.

4. Киреев В.И.,Пантелеев А.В. Численные методы в примерах и задачах.- М.: МАИ, 2000.- 376с.

5. Очков В.Ф. Современные информационные технологии в теплоэнергетике.- М.: МЭИ, 2007.- 67с.

6. Васильков Ю.В. Компьютерные технологии вычислений в математическом моделировании.- М.: ВШ, 2001.- 256 с.

7. Соболь Б.В. Методы оптимизации: Практикум.- Ростов н/Д.: Феникс, 2009.- 380с.

8. Основы современных компьютерных технологий. / Под ред.

А.Д. Хоменко.- СПб.: КОРОНА, 2005.- 672с.

9. Кирьянов Д.В. Mathcad - 14.- СПб.: БХВ - Петербург, 2007.-704с.

10. Охорзин В.А. Компьютерное моделирование в системе Mathcad.-М.: Финансы и статистика, 2006.-144с.

11. Голицина О.В. Информационные технологии. – М.: ФОРУМ: ИНФРА - М, 2008.- 608 с.

12. Максимов Н.В. Технические средства информатизации.- М.: ФОРУМ: ИНФРА - М, 2008.- 6592 с.

13. Теплоэнергетика и теплотехника. Общие вопросы: Справочник / Под ред. А.В. Клименко, В.М. Зорина. - М.: МЭИ, 1999. - 528 с.

14. Пасконов В.М., Полежаев В.И., Чудов Л.А. Численное моделирование процессов тепло - и массообмена. – М.: Наука, 1984.- 288с.

15. Патанкар С. Численные методы решения задач теплообмена и динамики жидкости. – М.: Энергоатомиздат, 1984.- 152 с.

16. Андерсон Д, Таннехилл Дж. Вычислительная гидромеханика и теплообмен. – М.: Мир, 1990.ч.1, 2 -728 с.

17. Основные процессы и аппараты химической технологии: Пособие по проектированию / Под. ред. Ю.И. Дытнерского. – М.: Химия, 1991.- 496 с.

18. Кафаров В.В., Глебов М.Б. Математическое моделирование основных процессов химических производств. – М.: ВШ.,1991.- 400 с.

19. Зайцев А.И. и др Математическое моделирование источников энергоснабжения промышленных предприятий. - М.: Энергия, 1991.-163 с.

20. Клима И. Оптимизация энергетических систем. - М.: ВШ, 1991.- 247 с.

21. Рыжиков Ю.И. Решение научно-технических задач на персональном компьютере. – СПб.: КОРОНА, 2000.- 272 с.

22. Шуп Т. Е. Прикладные численные методы в физике и технике. - М.: ВШ, 1990.- 255 с.

23. Ларсен Р. Инженерные расчеты в в Excel.- М.:. ИД Вильямс, 2002.-545с.

24. Васильев А.Н. Excel-2007 на примерах.- СПб.: БХВ Петербург, 2007.- 656с.

25. Кульгин Н Б Программирование в Turbo Pascal 7.0 и Delphi.- СПб.: БХВ Петербург, 2007.-400с.

26. Борисова Н.Г. Компьютерные технологии в теплоэнергетических расчетах. Методические указания к выполнению лабораторных работ. – А.: АИЭС, 2005.-36с.

 

 

Содержание

Лекция 1 Введение. Компьютерные технологии в моделировании теплоэнергетических систем, процессов и установок. Модели и виды моделирования…………………………………………………………………
Лекция 2 Математическое и физическое моделирование в теплоэнергетике. Процесс разработки и использования математических моделей…………………………………………………………………………
Лекция 3 Численные методы в математическом моделировании теплотехнических задач и их программная реализация. Методы интерполирования…………………………………………………………….
Лекция 4 Численное интегрирование в теплотехнических расчетах. Методы численного интегрирования…………………………………………
Лекция 5 Численные методы нахождение корней алгебраических и трансцендентных уравнений………………………………………………….
Лекция 6 Численные методы решения систем алгебраических уравнений……………………………………………………………………..
Лекция 7 Численные методы решения обыкновенных дифференциальных уравнений……………………………………………………………………….
Лекция 8 Численные методы решения краевых задач………………………
Лекция 9 Численные методы решения задач оптимизации………………….
Список литературы…………………………………………………………….