Лекция 1
Рисунок 1.1 - Классификация видов моделирования
Поскольку все процессы могут протекать при наличии или отсутствии случайных воздействий, их моделирование носит детерминированный или стохастический характер. Динамическое или статическое моделирование определяется стационарностью и нестационарностью процессов в исследуемом объекте. Периодичность функционирования объекта-оригинала отражается дискретным, дискретно-непрерывным и непрерывным моделированием.
Наглядное моделирование связано с описанием модели на основе представлений, гипотез, выдвигаемых человеком, и применения аналогий различных уровней.
Символьное моделирование отображает свойства объекта-оригинала определенной заранее отработанной системой символов.
Модели на микроуровне обычно формализуют объекты с распределенными параметрами и описываются системами дифференциальных уравнений в частных производных.
Модели на макроуровне обычно представляются обыкновенными дифференциальными уравнениями (задача Коши и краевая задача) и алгебраическими уравнениями. Они используются для моделирования процессов с сосредоточенными параметрами в стационарной и нестационарной постановках.
Модели на метауровне создаются для сложных технических объектов и используются в основном при моделировании систем массового обслуживания и систем автоматического управления.
Имитационное моделирование заключается в создании модели-имитатора работы сложных (чаще при наличии стохастических факторов) систем и процессов при неполных знаниях о ряде процессов в моделируемых объектах. Они не позволяют в отличие от аналитических моделей формировать решение в обычном виде, но за счет перебора вариантов позволяют выбрать приемлемое решение.
Комбинированное моделирование состоит из аналитического моделирования, включая элементы имитационного моделирования, и наоборот.
Реальное моделирование представляет разработку физических полноразмерных или масштабных моделей агрегатов (процессов).
В 2007г. кафедрами ТЭУ и ПТЭ приобретен программный продукт МЭИ «ТВТ Shell» и материалы Электронной Энциклопедии Энергетики.
Электронная Энциклопедия Энергетики включает следующие разделы: общие вопросы теплоэнергетики; теоретические основы теплотехники; тепломеханическое оборудование ТЭС; теплообменное оборудование ТЭС; водоподготовка; водно-химический режим; КИП и автоматика; энергосбережение, экология и охрана труда; топливоиспользование и технология масел; эксплуатация оборудования; тепловые сети. Кроме того, энциклопедия содержит виртуальные лабораторные работы, программы тестирования и тренажеры.
Достаточно большое количество материалов по применению компьютерных технологий в теплоэнергетике и теплотехнике представлено в настоящее время в Интернете. Это – интерактивные справочники по теплоэнергетике и теплотехнике, каталоги энергетического оборудования, нормативно-правовая документация (ГОСТ, СНиП, СН, СО, РД и т.п.), типовые энергетические характеристики и их расчеты, тренажеры и программно-технические средства для производственного персонала энергетических предприятий, таблицы теплофизических свойств энергоносителей и т.д.
Литература: [1],[5],[8],[11],[13],[18].
Лекция 2
Лекция 3
Интерполирование функций
Интерполяция применяется во многих задачах, связанных с вычислениями. Укажем некоторые из этих задач.
Обработка физического эксперимента – построение приближенных формул для характерных величин по табличным данным, полученным экспериментально.
Построение приближенных формул по данным вычислительного эксперимента. Здесь возникают нестандартные задачи интерполяции, так как обычно записываются формулы, с возможно более простой структурой.
Субтабулирование - сгущение таблиц применяется в тех случаях, когда непосредственное вычисление функций трудно или когда имеется мало экспериментальных данных. В РС вводится небольшая таблица, а нужные при расчетах значения функции находятся по мере необходимости по интерполяционной формуле.
Интерполяция применяется также в задаче обратного интерполирования: задана таблица уi = y(xi); найти хi как функцию от уi. Примером обратного интерполирования может служить задача о нахождении корней уравнения.
Интерполяционные формулы используются также при вычислении интегралов, при написании разностных аппроксимаций для дифференциальных уравнений на основе интегральных тождеств.
В общем случае при постановке задачи приближения нужно следовать по алгоритму:
- определить какой класс приближенных функций нужно выбрать;
- выбрать критерий близости («согласия») исходной и приближающей функции (совпадение в узловых точках – метод Лагранжа, или метод наименьших квадратов);
- указать правило, позволяющее с заданной степенью точности, получить значение функции в промежуточных точках между узлами (какие узлы использовать и как их расположить).
Часто требуется восстановить функцию f(x) для всех значений х на отрезке а ≤ х ≤ b, если известны ее значения в некотором конечном числе точек этого отрезка. Эти значения могут быть найдены в результате наблюдений (измерений) в каком-то натурном эксперименте, либо в результате вычислений. Кроме того, может оказаться, что функция f(x) задается формулой и вычисления ее значений по этой формуле очень трудоемки, поэтому желательно иметь для функции более простую (менее трудоемкую для вычислений) формулу, которая позволяла бы находить приближенное значение рассматриваемой функции с требуемой точностью в любой точке отрезка. В результате возникает следующая математическая задача.
Пусть на отрезке а £ x £ b задана сетка ω ={х0 = а < х1 <¼< хn = b } и в ее узлах заданы значения функции у (х), равные у (х0) = у0, …, у(хi) = уi, …, у(хn) = уn. Требуется построить интерполянту – функцию f(х), совпадающую с функцией у(х) в узлах сетки:
f (xi) = yi, i = 0, 1, …, n (3.1)
Основная цель интерполяции – получить быстрый (экономичный) алгоритм вычисления значений f(x) для значений х, не содержащихся в таблице данных.
Основной вопрос: как выбрать функцию - интерполянту f(х) и оценить погрешность у(х) - f(х)?
Интерполирующие функции f(х), как правило, строятся в виде линейных комбинаций некоторых элементарных функций:
f(x) = 
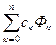
 ,
,
где {Ф  (х)} - фиксированные линейно независимые функции;
(х)} - фиксированные линейно независимые функции;
с0, с1, …, сn - не определенные пока коэффициенты. 

Из условий (3.1) получим систему n+1 уравнений относительно коэффициентов {с  }:
}:
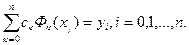
Предположим, что система функций Ф  (х) такова, что при любом выборе узлов а = х0< х1 < …< хn = b отличен от нуля определитель системы:
(х) такова, что при любом выборе узлов а = х0< х1 < …< хn = b отличен от нуля определитель системы:
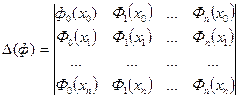
 Тогда по заданным уi (i = 0,1,…, n) однозначно определяются коэффициенты с
Тогда по заданным уi (i = 0,1,…, n) однозначно определяются коэффициенты с  (
( = 0, 1, …, n).
= 0, 1, …, n).
В качестве системы линейно независимых функций {Ф  (х)} чаще всего выбирают: степенные функции Ф
(х)} чаще всего выбирают: степенные функции Ф  (х) = х
(х) = х  (в этом случае f = Pn (x) – полином степени n); тригонометрические функции { Ф
(в этом случае f = Pn (x) – полином степени n); тригонометрические функции { Ф  (х) = соs kх, sin kx} (в этом случае f - полином тригонометрический). Используются также рациональные функции
(х) = соs kх, sin kx} (в этом случае f - полином тригонометрический). Используются также рациональные функции

и другие виды интерполирующих функций.
Рассмотрим полиномиальную интерполяцию.
Известно, что любая непрерывная на отрезке [а, b] функция f(x) может быть хорошо приближена некоторым полиномом Рn(х).
Будем искать интерполяционный полиномв виде
Рn(x) =  (3.2)
(3.2)
где с  - неопределенные пока коэффициенты.
- неопределенные пока коэффициенты.
Полагая f (xi) = yi, получим систему линейных уравнений вида
 с0+с1 х0+…+сnх0n= y0,
с0+с1 х0+…+сnх0n= y0,
с0+с1 х1+…+сnх1n= y1,
…………………..…,
с0+с1 хn+…+сnхnn= yn.
Определитель этой системы отличен от нуля, т.е. полином вида (3.2) существует и единственен. Форм записей такого полинома существует множество.
В качестве базиса {Ф  (х)} мы взяли базис из одночленов 1, х, х2, …, хn. Для вычислений более удобным является базис полиномов Лагранжа {l
(х)} мы взяли базис из одночленов 1, х, х2, …, хn. Для вычислений более удобным является базис полиномов Лагранжа {l  (x)} степени n или коэффициентов Лагранжа:
(x)} степени n или коэффициентов Лагранжа:
l  (xi) = 1, если i = k,
(xi) = 1, если i = k,
0, если i ≠ k, i, k = 0, 1, …, n.
Нетрудно видеть, что полином степени n
l  (x) = l
(x) = l  (x) =
(x) = 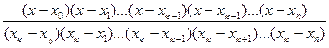
удовлетворяет этим условиям. Полином l  (x), очевидно, определяется единственным образом.
(x), очевидно, определяется единственным образом.
Полином l  (x) y
(x) y  принимает значение у
принимает значение у  в точке х
в точке х  и равен нулю во всех остальных узлах х
и равен нулю во всех остальных узлах х  при j ¹ k. Отсюда следует, что интерполяционный полином
при j ¹ k. Отсюда следует, что интерполяционный полином
Рn(x) =  (3.3)
(3.3)
имеет степень не выше n и Рn (xi) = yi. Формулу (3.3) называют формулой Лагранжа. К достоинствам формулы можно отнести то, что число арифметических действий для вычисления пропорционально n2.
Для оценки близости полинома Рn(х) к функции f(х) предполагают, что существует (n+1)-я непрерывная производная f(n+1) (х).
Сплайн - интерполяция
Приближение сплайнами - кусочно-полиномиальное приближение функции f(x) по ее значениям в узлах. Степень полинома на каждом участке одинакова, и называется порядком сплайна. Часто между любыми соседними уздами сетки функция интерполируется кубическим полиномом - кубическая сплайн-интерполяция. Коэффициенты кубического полинома на каждом участке определяются из условий сопряжения (согласования) в узлах.
f(xi)=yi, f'(xi-0) = f'(xi+0), f"(xi-0) = f"(xi+0), для i = 0,1,…, n-1.
На границе участка ставятся условия f"(x0)=0, f"(xn)=0.
Условия согласования звеньев сплайна с исходной функцией используются для вывода формулы одного звена на заданном отрезке. Количество согласований соответствует степени сплайна.
Компьютерная реализация методов интерполирования в Excel описана в [23-24,26].
Литература: [1 - 4],[6],[22-24].
Лекция 4
Формула прямоугольников
Впишем в каждую полоску прямоугольник. Для нахождения площади такого прямоугольника найдем координату средней точки хср = (xi+xi+1)/2 и значение функции в ней f (xср). Площадь под кривой определяется так
I=ΣIi= Σf((xi+xi+1 )/2)*(xi+1- xi) (4.3).
Формула (4.3) - формула прямоугольников.
Оценим погрешность метода прямоугольников, для чего разложим функцию в ряд Тейлора и отбросим соответствующие члены ряда, содержащие h в степени больше 3.
Эта погрешность может быть определена так:
ei = - (h3/24)* f ′′ (xi),
ε = ∑ ei = - (h2/24)* (b-a) * f ′′ (ξ), (4.4).
где ξ є [ a, b ].
Метод трапеций
Впишем в каждую полоску трапецию. Площадь под кривой определяется так
I=ΣIi= Σ1/2 (f (xi+1)- f((xi)) *(xi+1- xi) + f(xi) *(xi+1- xi)
Формула трапеций на равномерной сетке шагом h =(xi+1- xi):
I = ∑ сi * f (xi) = h/2*(y0 + 2y1 + 2y2 +... + yn) (4.5).
i
h = (b -а)/ n; у0 = f (x0); у1 = f (x1) и т.д.
Оценим погрешность метода трапеций, для чего разложим функцию в ряд Тейлора и отбросим соответствующие члены ряда, содержащие h в степени больше 3. Эта погрешность может быть определена так:
ei = - (h3/12)* f ′′ (xi)
ε = ∑ ei = - (h2/12)* (b-a) * f ′′ (ξ), где ξ є [ a, b ] (4.6).
4.2.3 Метод Симпсона
Этот метод аналогичен правилу трапеций в той части, где интегрирование производится путём разбиения общего интервала на множество более мелких отрезков. Однако теперь для вычисления площади каждой полоски через каждые три последовательные ординаты разбиения проводят квадратичную параболу.
Предположим, что число отрезков чётное:
n = (b-a) / h.
Воспользуемся методом трапеции:
I h= h/2*(y0 + 2y1 + 2y2 +... + yn) (4.7)
Площадь под кривой I = I h+с h2 (4.8)
Увеличим шаг в два раза k = 2h:
I k= k/2*(y0 + 2y2 + 2y4 +... + yn) (4.9)
Площадь под кривой I = Ik+с k2. (4.10)
Исключив из системы уравнений (4.8) и (4.10) с, получим формулу Ричардсона для лучшего приближения интеграла
I = I h+ (I h - Ik)/ (k2/ h2-1) (4.11)
Подставим (4.7) и (4.9) в (4.11) получаем формулу Симпсона
I = h/3*(y0 + 4y1 + 2y2 + 4y3 + 2y4 +... + yn) (4.12)
Ошибка ограничения, допускаемая в методе Симпсона
ei = - (h4/180)* f (IV) (xi)
ε = ∑ ei = - (h4/180)* (b-a) * f (IV) (ξ), (4.13)
где ξ є [a, b].
Метод трапеций и Симпсона наиболее часто используется при численном интегрировании.
Оценка погрешности ограничения рассмотренных методов численного интегрирования по выражениям (4.4), (4.6) и (4.13) оказываются малоэффективными из-за трудностей оценки производных высокого порядка подынтегральных функций. На практике для достижения требуемой точности прибегают к методу последовательного удвоения числа шагов. Задают значение допустимой погрешности ε и число интервалов разбиения n (шаг интегрирования h) находят In. Удваивают число интервалов (шаг интегрирования h/2) и находят I 2n. Оценивают погрешность Δ=(In- I 2n)/3 – для метода трапеций и Δ=(In- I 2n)/15 – для метода Симпсона. Если Δ≥ ε, количество интервалов еще раз удваивают. Вычисления заканчивают при выполнении условия Δ< ε.
4.2.4 Метод Гаусса
Гауссом предложен метод, позволяющий уменьшить ошибку ограничения при заданном числе интервалов за счет расположения концов интервалов там, где это требуется из условий достижения наивысшей точности интегрирования.
В заданном интеграле b
I=ò f(x)dx,
a
изменим пределы интегрирования так, чтобы они стали равны +1и –1, для чего введем новую переменную μ = (2х- (b+a))/(b-a)
1
I=ò φ (μ)dμ, где φ (μ)=(1/2)(b-a) f((b-a) μ /2+(b+a)/2).
-1
Можно показать, что
1
I=ò φ (μ)dμ = φ (-1/√3) + φ (1/√3) +ε, (4.14)
-1
где ε= φ (IV)/135.
(4.14)– формула Гаусса для двух ординат.
Можно вывести Гауссовы формулы численного интегрирования более высокого порядка с использованием полиномов Лежандра [1]. На практике предпочтение отдается методу Симпсона.
Интегрирование по квадратурным формулам сопровождается ошибками округления. Они носят случайный характер и с увеличением числа интервалов разбиения n возрастают пропорционально √n. Для функций высокой гладкости формула Гаусса дает значительно более точные результаты, чем формула Симпсона при одинаковом числе узлов, а последняя более точные, чем формула трапеций. Формула Гаусса обеспечивает высокую точность при небольшом числе узлов. Формула Симпсона в достаточной степени точна при умеренном числе узлов и поэтому получила широкое применение. Компьютерная реализация методов интегрирования описана в [9], [23-26].
Литература: [1-4],[6],[22-24].
Лекция 5
Алгоритм метода дихотомии.
1. Вычисляют значения функции через равные интервалы значений х до смены знака, при переходе от f(xn) к f(xn+1)
2. Вычисляют среднее значение аргумента xср и находят f(xср).
3. Если знак f(xср) совпадает со знаком f(xn), то в дальнейших расчетах вместо xn используют xcp. Если f(xcp) совпадает с f(xn+1), то вместо xn+1 берут xcp.
4. Интервал, в котором заключено значение корня, сужается. Если f(xcpk) ≤ 0 + ε, где ε положительное наперед заданное достаточное малое число – точность расчета, то процесс заканчивается за k итераций, при этом ширина интервала уменьшается в 2k раз. Если f(xcpk) > 0 + ε, повторяют пп.2-3 алгоритма.
Метод имеет линейную, но безусловную сходимость, и его погрешность за каждую итерацию уменьшается в два раза.
Метод не применим к корням четной кратности, т.е. тогда когда, f(x)=g(x)(x-x1)m, где x1 корень кратности m.
Метод хорд
В основе этого метода, как и в методе дихотомии, лежит линейная интерполяция по двум значениям функции, имеющим противоположные знаки, но он обеспечивает более быстрое нахождение корня.

Y f(хn+1)
x1* x2* x3* x4* x*
хn хn+1 X
f(хn)
Рисунок 5.3 – Геометрическая интерпретация метода хорд
Алгоритм метода хорд.
1. Вычисляют значения функции через равные интервалы значений х до смены знака при переходе от f (xn) к f (xn+1).
2. Прямая, проходящая через эти две точки, пересекает ось х в точке
х* = xn – f (xn)(xn+1 - xn)/ (f (xn+1) – f (xn)) (5.1)
3. Находят значение f (xk*), которое сравнивают с известными f (xn),
f (xn+1). Если знак f(xк*) совпадает со знаком f(xn), то в дальнейших расчетах вместо xn используют xk*. Если f(xk*) совпадает с f(xn+1), то вместо xn+1 берут xk*.
4. Проверяют близость f(xk*) к нулю c заданной точностью ε. Если f(xk*) ≤ 0 + ε, то процесс заканчивается за k итераций. Если f(xk*) > 0 + ε, повторяют пп.2-3 алгоритма.
В знаменателе формулы (5.1) стоит разность значений функций. Вдали от корня она несущественна, но вблизи корня эти значения близки и малы. Возникает потеря значащих цифр, приводящая к «разболтке» счета. Это ограничивает точность, с которой можно найти корень. Для простых корней это ограничение невелико, а для кратных – существенно. Можно использовать метод Гарвика. Выбирают не очень малое ε, ведут итерации до выполнения условия |xn+1 - xn| < ε и затем продолжают расчет до тех пор, пока |xn+1 - xn| убавает.
Метод Ньютона
Метод последовательных приближений, разработанный Ньютоном, используется наиболее часто среди всех итерационных алгоритмов.
Функция f(x), дважды дифференцируемая на отрезке [a, b], который содержит корень х*. При этом f(x*)=0. Для определения интервала, в котором заключен корень, в методе Ньютона не требуется находить значения функции с противоположными знаками. Вместо интерполяции по двум значениям функции будем проводить экстраполяцию с помощью касательной в данной точке.
 Y
Y

 М0
М0
х*


 X
X
х1 х2 х0
М1
Рисунок 5.4 – Геометрическая интерпретация метода Ньютона
Алгоритм метода:
1. Находят значение xn+1, которое соответствует точке, в которой касательная к кривой в точке xn пересекает ось х
xn+1 = xn - f(xn)/f ′(xn) (5.2)
2. Процедуру повторяют до выполнения условия близости функции к нулю с заданной точностью f(xn) ≈ ε
Быстрота сходимости метода Ньютона в большой мере зависит от выбора исходной точки. Если в процессе итераций тангенс угла наклона касательной f ′(xn) обращается в ноль, то применение метода усложняется. В случае бесконечно больших f ′′(x) метод также недостаточно эффективен. При кратности корней (условие f (x)=f ′(x)=0) метод Ньютона не обеспечивает сходимости.
Метод секущих
Одним из недостатков метода Ньютона является необходимость дифференцирования заданной функции f(x). Если нахождение производной затруднено, можно воспользоваться некоторым приближением, которое положено в основу метода секущих. Заменим производную f ′(xn) для расчета
xn+1 = xn - f(xn)/f ′(xn) разностью последовательных значений функции, отнесенных к разности последовательных значений аргумента, т.е. разделенной разностью первого порядка
F*(xn)= (f(xn)- f(xn-1))/(xn- xn-1),
тогда
xn+1 = xn - f(xn)/ F*(xn). (5.3)
Схема алгоритма остается, как и в методе Ньютона, изменяется только вид итерационной формулы (5.3).
5.6 Метод простой итерации (последовательных приближений)
Для применения этого метода уравнение f(x)=0 приводится к виду
х = g(х). Задаются начальным значением х0, а последующие приближения вычисляются с помощью итерационной процедуры
xn+1= g(хn). (5.4)
Для сходимости метода необходимо выполнение условия
0< g′ (хn)<1
 Y
Y

 x
x


 g(x)
g(x)

 X
X
х0 х1 х2
Рисунок 5.5 – Геометрическая интерпретация метода простых итераций
Компьютерная реализация методов в Excel описана в [9], [23-24, 26].
Литература: [1-4],[6], [9], [14-17], [23-24].
Лекция 6
Метод Зейделя


 Суть итерационного метода Зейделя состоит в том, что задается некоторый произвольный вектор х [0], являющийся началом приближения к искомому решению х*. Затем строят последовательность приближенных значений {x[k]}, где k=0,1,2,…, сходящихся к х*
Суть итерационного метода Зейделя состоит в том, что задается некоторый произвольный вектор х [0], являющийся началом приближения к искомому решению х*. Затем строят последовательность приближенных значений {x[k]}, где k=0,1,2,…, сходящихся к х*
lim x[k]=x*, при k→∞.
Последовательность векторов х[0], x[1], …, x[k] сходится к х* в том случае, если для любого ε > 0 существует натуральное число N, начиная с которого (k ≥ N), выполняется условие
||x*-x[k]|| < ε,
где ||·|| - норма вектора.
6.3.1 Алгоритм метода Зейделя
А) Исходную систему линейных алгебраических уравнений
 x1+c12x2+c13x3+… +c1nxn=d1
x1+c12x2+c13x3+… +c1nxn=d1
x2+c21x1+c23x3+… +c2nxn=d2
...................... (6.13)
cn1x1+cn2x2+cn3x3+… +xn=dn
разрешают относительно неизвестных х1, х2, …, хn и приводят к виду:
 x1=c12x2+… +c1nxn+d1
x1=c12x2+… +c1nxn+d1
x2=c21x1+… +c2nxn+d2 (6.14)
..................
xn=cn1x1+… +cnnxn+dn
Такое преобразование всегда можно выполнить, если определитель системы отличен от нуля.
Б) Задают начальные значения вектора x[0]={x1[0], x2[0], …, xn[0]}. Начальный вектор может быть выбран произвольно, однако необходимо использовать всю информацию, чтобы вектор x[0] был близок к х*.
В) В первое уравнение системы (6.14) подставляют координаты точки x[0] и вычисляют значение первой координаты:
x1[1]=c12x2[0]+c13x3[0]+… +c1nxn[0]+d1.
В следующее уравнение подставляем х1[1] и значения xn[0]:
х2[1]=c21x1[1]+c23x3[0]+… +c2nxn[0]+d2.
Аналогично для xn[1]:
xn[1]=cn1x1[1]+cn2x2[1]+… +dn
В результате будет найдено
x[1]={x1[1],…,xn[1]}.
Г) Начальный вектор x[0] заменяют x[1] и вычисляют следующее приближение. В общем случае k+1 приближение определяется по формуле:
 x1[k+1]=c12x2[k]+…+c1nxn[k]+d1
x1[k+1]=c12x2[k]+…+c1nxn[k]+d1
x2[k+1]=c21x1[k+1]+…+c2nxn[k]+d2
...........................
xn[k+1]=cn1x1[k+1]+…+dn
Итерационный процесс будет продолжаться до тех пор, пока все xi[k+1] не будут близки с xi[k], то есть выполнится условие:
 ||xi[k+1]-xi[k]|| < ε, (6.15)
||xi[k+1]-xi[k]|| < ε, (6.15)
где ε - точность вычисления.
Можно показать, что с помощью метода Зейделя строится сходящаяся к точному решению последовательность векторов {x[k]}, если матрица А системы уравнений удовлетворяет условию:
|aij| > |ai1| + |ai2| +…+ |ain|. (6.16)
Для всех i или хотя бы для одного i должно удовлетворятся условие:
|aii| > |ai1| + |ai2| +…+ |ain|. (6.17)
Лекция 7
Метод Эйлера
Дано уравнение у' = f(x,y) с начальным условием у(х0)= у0.
Рисунок 7.1-Геометрическая интерпретация метода Эйлера
В рассмотренном методе переход от точки (xi,yi), в точку (xi+1,yi+1), осуществляется путем смещения на вектор (h, К1). Ошибка метода имеет порядок h2, так как члены, содержащие h во второй и более высоких степенях, отбрасываются, кроме того метод часто оказывается неустойчивым – малая ошибка увеличивается с ростом х. Этот метод можно усовершенствовать различными способами [1].
Рассмотрим модифицированный метод Эйлера. Хотя тангенс угла наклона касательной к истинной кривой в исходной точке известен и равен y¢(x0), он изменяется в соответствии с изменением независимой переменной. Поэтому в точке (x0+h) наклон касательной уже не таков, каким он был в точке x0. Следовательно, при сохранении начального наклона касательной на всем интервале h в результаты вычислений вносится погрешность. Точность метода Эйлера можно существенно повысить, улучшив аппроксимацию производной. Это можно сделать, например, используя среднее значение производной в начале и в конце интервала. В модифицированном методе Эйлера сначала вычисляют значение функции в следующей точке по методу Эйлера
y*n+1=yn + hf (x n, y n ). (7.4)
Его используют для вычисления приближенного значения производной в конце интервала f(xn+1,y*n+1). Вычислив среднее между этим значением производной и ее значением в начале интервала, найдем более точное значение yn+1:
yn+1=yn+ (f (xn, yn)+f (xn+1,y*n+1))/2h. (7.5)
Модифицированный метод Эйлера имеет второй порядок точности, т.е погрешность метода имеет порядок h3.
Методы Рунге-Кутты
Наибольше распространение при решении обыкновенных дифференциальных уравнений получилметоды Рунге-Кутты.
В методах Рунге-Кутты более высокого порядка точности смещение из
точки (xi,yi), в точку (xi+1,yi+1) происходит не сразу, а через промежуточные точки (внутренние для интервала [хi,хi+1]), в каждой из которых определяется направление касательной. В результате смещение выполняется вдоль некоторого усредненного направления. Методы Рунге-Кутты дает набор формул для расчета координат внутренних точек, требуемых для реализации этой идеи. Так как существует несколько способов расположения внутренних точек и выбора относительных весов для найденных производных, то метод Рунге-Кутты, в сущности, объединяет целое семейство методов решения дифференциальных уравнений первого порядка, которым можно отнести метод Эйлера и его модификации.
Наиболее распространенным является метод Рунге-Кутты четвертого порядка точности, для которого ошибка на шаге имеет порядок h5.
В этом методе значения величины yi+1 рассчитывается по формуле
yi+1=yi+h (K1+2K2+2K3+K4)/6, (7.6)
где K1=f (x i, yi),
K2=f (xi+ h /2,yi+ h k1/2),
K3=f (xi+ h /2, yi+ h k2/2),
K4=f (xi+h, yi+ h k3).
Метод Рунге-Кутты применим к системам уравнений первого порядка, а также к уравнениям любого порядка, которые можно свести к системам уравнений первого порядка путем замены переменных.
Лекция 8
Лекция 9
Рисунок 9.8 - Линии уровня для овражного рельефа
(например, Ф(х,у) = 10(у - sinx)2+0,1x2)
Линии уровня для неупорядоченного рельефа, имеют много максимумов, минимумов и седловин.

y
• min
x
Рисунок 9.9 - Линии уровня для неупорядоченного рельефа
(например, Ф(х,у) = (1+ sin2x)(1+sin2y))
К численным методам решения задач оптимизации первого порядка относятся градиентные методы [].
Градиентные методы, а также численные методы решения задач условной оптимизации будут рассмотрены в курсе «Методы моделирования и оптимизации теплоэнергетических процессов и установок».
Компьютерная реализация методов в Excel описана в [9], [23-26].
Литература: [7], [20].
Список литературы
1. Амосов А.А. Вычислительные методы для инженеров.- М.: МЭИ, 2003. – 596с.
2. Пирумов У.Г. Численные методы. - М.: ДРОФА, 2007.- 221с.
3. Численные методы: Сборник задач /Под ред. У.Г. Пирумова. - М.: ДРОФА, 2007.- 144 с.
4. Киреев В.И.,Пантелеев А.В. Численные методы в примерах и задачах.- М.: МАИ, 2000.- 376с.
5. Очков В.Ф. Современные информационные технологии в теплоэнергетике.- М.: МЭИ, 2007.- 67с.
6. Васильков Ю.В. Компьютерные технологии вычислений в математическом моделировании.- М.: ВШ, 2001.- 256 с.
7. Соболь Б.В. Методы оптимизации: Практикум.- Ростов н/Д.: Феникс, 2009.- 380с.
8. Основы современных компьютерных технологий. / Под ред.
А.Д. Хоменко.- СПб.: КОРОНА, 2005.- 672с.
9. Кирьянов Д.В. Mathcad - 14.- СПб.: БХВ - Петербург, 2007.-704с.
10. Охорзин В.А. Компьютерное моделирование в системе Mathcad.-М.: Финансы и статистика, 2006.-144с.
11. Голицина О.В. Информационные технологии. – М.: ФОРУМ: ИНФРА - М, 2008.- 608 с.
12. Максимов Н.В. Технические средства информатизации.- М.: ФОРУМ: ИНФРА - М, 2008.- 6592 с.
13. Теплоэнергетика и теплотехника. Общие вопросы: Справочник / Под ред. А.В. Клименко, В.М. Зорина. - М.: МЭИ, 1999. - 528 с.
14. Пасконов В.М., Полежаев В.И., Чудов Л.А. Численное моделирование процессов тепло - и массообмена. – М.: Наука, 1984.- 288с.
15. Патанкар С. Численные методы решения задач теплообмена и динамики жидкости. – М.: Энергоатомиздат, 1984.- 152 с.
16. Андерсон Д, Таннехилл Дж. Вычислительная гидромеханика и теплообмен. – М.: Мир, 1990.ч.1, 2 -728 с.
17. Основные процессы и аппараты химической технологии: Пособие по проектированию / Под. ред. Ю.И. Дытнерского. – М.: Химия, 1991.- 496 с.
18. Кафаров В.В., Глебов М.Б. Математическое моделирование основных процессов химических производств. – М.: ВШ.,1991.- 400 с.
19. Зайцев А.И. и др Математическое моделирование источников энергоснабжения промышленных предприятий. - М.: Энергия, 1991.-163 с.
20. Клима И. Оптимизация энергетических систем. - М.: ВШ, 1991.- 247 с.
21. Рыжиков Ю.И. Решение научно-технических задач на персональном компьютере. – СПб.: КОРОНА, 2000.- 272 с.
22. Шуп Т. Е. Прикладные численные методы в физике и технике. - М.: ВШ, 1990.- 255 с.
23. Ларсен Р. Инженерные расчеты в в Excel.- М.:. ИД Вильямс, 2002.-545с.
24. Васильев А.Н. Excel-2007 на примерах.- СПб.: БХВ Петербург, 2007.- 656с.
25. Кульгин Н Б Программирование в Turbo Pascal 7.0 и Delphi.- СПб.: БХВ Петербург, 2007.-400с.
26. Борисова Н.Г. Компьютерные технологии в теплоэнергетических расчетах. Методические указания к выполнению лабораторных работ. – А.: АИЭС, 2005.-36с.
Содержание
| Лекция 1 Введение. Компьютерные технологии в моделировании теплоэнергетических систем, процессов и установок. Модели и виды моделирования…………………………………………………………………
|
|
| Лекция 2 Математическое и физическое моделирование в теплоэнергетике. Процесс разработки и использования математических моделей…………………………………………………………………………
|
|
| Лекция 3 Численные методы в математическом моделировании теплотехнических задач и их программная реализация. Методы интерполирования…………………………………………………………….
|
|
| Лекция 4 Численное интегрирование в теплотехнических расчетах. Методы численного интегрирования…………………………………………
|
|
| Лекция 5 Численные методы нахождение корней алгебраических и трансцендентных уравнений………………………………………………….
|
|
| Лекция 6 Численные методы решения систем алгебраических
уравнений……………………………………………………………………..
|
|
| Лекция 7 Численные методы решения обыкновенных дифференциальных уравнений……………………………………………………………………….
|
|
| Лекция 8 Численные методы решения краевых задач………………………
|
|
| Лекция 9 Численные методы решения задач оптимизации………………….
|
|
| Список литературы…………………………………………………………….
|
|
Лекция 1
Тема: Введение. Компьютерные технологии в моделировании теплоэнергетических систем, процессов и установок. Модели и виды моделирования.
План: Введение. Цели и задачи курса. Политика курса. Состояние и перспективы использования компьютерных технологий в моделировании теплоэнергетических систем, процессов и установок. Классификация моделей и видов моделирования.
Курс «Компьютерные технологии в теплоэнергетических расчетах» является дисциплиной по выбору для студентов бакалавриата и включен в учебные планы в качестве базовой дисциплины.
Цель курса – формирование знаний, умений и навыков применения компьютерных технологий для расчета объектов те






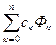
 ,
, (х)} - фиксированные линейно независимые функции;
(х)} - фиксированные линейно независимые функции;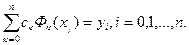
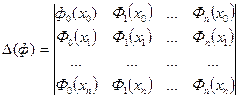

 (3.2)
(3.2) - неопределенные пока коэффициенты.
- неопределенные пока коэффициенты. с0+с1 х0+…+сnх0n= y0,
с0+с1 х0+…+сnх0n= y0,
 (x) =
(x) = 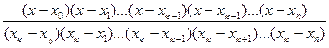
 при j ¹ k. Отсюда следует, что интерполяционный полином
при j ¹ k. Отсюда следует, что интерполяционный полином (3.3)
(3.3)
 Y
Y
 М0
М0



 X
X Y
Y
 x
x


 g(x)
g(x)
 X
X
 x1+c12x2+c13x3+… +c1nxn=d1
x1+c12x2+c13x3+… +c1nxn=d1 x1=c12x2+… +c1nxn+d1
x1=c12x2+… +c1nxn+d1 x1[k+1]=c12x2[k]+…+c1nxn[k]+d1
x1[k+1]=c12x2[k]+…+c1nxn[k]+d1



