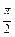Лабораторная работа
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА
Теоретическая часть
Криволинейный интеграл первого рода
Определение
Пусть в каждой точке гладкой кривой L = AB в плоскости Оху задана непрерывная ограниченная функция двух переменных f (x, y). Непрерывная кривая x = x (t), y = y (t) называется гладкой на отрезке a ≤ t ≤ β, если функции
 x = x (t) и y = y (t) имеют на этом отрезке непрерывные производные x ¢(t) и y ¢(t), одновременно не равные нулю. Произвольно разобьем кривую L на n частей точками А = М 0, М 1, М 2, …, Мn = B. На каждой из полученных дуг Мi -1, Мi выберем произвольную точку Ri (ξi, ηi) (рис.1) и составим сумму
x = x (t) и y = y (t) имеют на этом отрезке непрерывные производные x ¢(t) и y ¢(t), одновременно не равные нулю. Произвольно разобьем кривую L на n частей точками А = М 0, М 1, М 2, …, Мn = B. На каждой из полученных дуг Мi -1, Мi выберем произвольную точку Ri (ξi, ηi) (рис.1) и составим сумму
Sn =  Δ li, (1)
Δ li, (1)










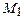
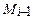











 где Δ li = Мi -1 Мi – длина дуги Мi -1, Мi.
где Δ li = Мi -1 Мi – длина дуги Мi -1, Мi.
Сумма (1) называется интегральной
суммой первого рода для функции f (x, y) по
 кривой L. Пусть λ =
кривой L. Пусть λ =  Δ li - наибольшая
Δ li - наибольшая
из длин дуг Мi -1, Мi. Если при λ → 0 (n →∞)
существует предел интегральных сумм Sn, Рис.1.
не зависящий ни от способа разбиения
кривой L на части, ни от выбора точек Ri (ξi, ηi) на них, то этот предел называется криволинейным интегралом первого рода (или криволинейным
интегралом по длине дуги) от функции f (x) по кривой L и обозначается
 или
или 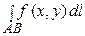 .
.
Вычисление
Вычисление криволинейного интеграла первого рода сводится к вычислению определенного интеграла. А именно:
1. Если кривая L задана явно непрерывно дифференцируемой функцией у = у (х), х  [ a, b ], то
[ a, b ], то
 =
=  . (2)
. (2)
2. Если кривая L задана параметрически, т.е. в виде x = x (t), y = y (t), где
x = x (t), y = y (t) – непрерывно дифференцируемые функции на некотором отрезке [ a, β ], то
 =
=  . (3)
. (3)
3. Если плоская кривая L задана полярным уравнением r = r (φ), где
φ [ a, β ], то
 =
=  . (4)
. (4)
Криволинейный интеграл второго рода
Определение

 Пусть L = AB – гладкая кривая, а Р (x, y) и Q (x, y) – некоторые функции, определенные в точках кривой L. Разобьем кривую L точками А = М 0, М 1, М 2, …, Мn = B в направлении от точки А к точке В на n произвольных дуг Мi -1, Мi с длинами Δ li (i = 1, 2, …, n).На каждой из полученных дуг Мi -1, Мi выберем произвольную точку Ri (ξi, ηi) (рис.2) и составим сумму
Пусть L = AB – гладкая кривая, а Р (x, y) и Q (x, y) – некоторые функции, определенные в точках кривой L. Разобьем кривую L точками А = М 0, М 1, М 2, …, Мn = B в направлении от точки А к точке В на n произвольных дуг Мi -1, Мi с длинами Δ li (i = 1, 2, …, n).На каждой из полученных дуг Мi -1, Мi выберем произвольную точку Ri (ξi, ηi) (рис.2) и составим сумму




























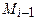
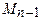












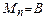 Sn =
Sn =  Δ xi + Q (ξi, ηi) Δ yi ] (2)
Δ xi + Q (ξi, ηi) Δ yi ] (2)
где Δ хi = хi – хi -1 – проекция дуги Мi -1, Мi на
ось Ох, а Δ уi = уi – уi -1 – на ось Оу. Сумма (2)
называется интегральной суммой второго рода
для вектор-функции F (x, y) = Р (x, y) i + Q (x, y) j
по  кривой L. Пусть λ =
кривой L. Пусть λ =  Δ li - наибольшая
Δ li - наибольшая
из длин дуг Мi -1, Мi. Если при λ → 0
существует предел интегральных сумм (2),
не зависящий ни от способа разбиения Рис.2.
кривой L на дуги, ни от выбора точек Ri (ξi, ηi)
на них, то этот предел называется криволинейным интегралом второго рода (или криволинейным интегралом по координатам) от вектор-функции F (x, y) = Р (x, y) i + Q (x, y) j по кривой L и обозначается
 + Q (x, y) dy или
+ Q (x, y) dy или  + Q (x, y) dy.
+ Q (x, y) dy.
Вычисление
1. Если кривая L задана явно непрерывно дифференцируемой функцией у = у (х), х  [ a, b ], то
[ a, b ], то
 + Q (x, y) dy =
+ Q (x, y) dy =  . (5)
. (5)
2. Если кривая L задана параметрически в виде x = x (t), y = y (t), где
x = x (t), y = y (t) – непрерывно дифференцируемые функции на некотором отрезке [ a, β ], то
 + Q (x, y) dy =
+ Q (x, y) dy =  . (6)
. (6)
Var
x0,xn,dx,dy,s,xi,xc,yc,dl,tr: real;
n,i: integer;
function piv(x,y,dl: real): real; {подынтегральное выражение x / y dl }
Begin
piv:=x/y*dl
end;
function put(x: real): real; {кривая интегрирования sqrt(2x)}
Begin
put:= sqrt(2*x)
end;
Begin
writeln (‘введите пределы интегрирования по х: x0 и xn’);
read (x0,xn); {ввод x0,xn }
tr:=(17*sqrt(17) – 5*sqrt(5))/6; (аналитическое решение)}
writeln (‘введите число разбиений n отрезка [a,b]’);
read (n); {ввод n }
writeln( ‘ Р Е З У Л Ь Т А Т Ы’);{впереди 20 пробелов}
writeln;
writeln (‘ n точн.знач. числ.реш. абс.ош. отн.ош’);{4,7,2,3,5 пробелов}
writeln;
dx:=(xn–x0)/n;
s:=0; {интегральная сумма}
xi:=x0; {начальная точка частичных отрезков}
xс:=x0–dx/2; {серединная точка частичных отрезков}
for i:=1 to n do
Begin
xс:=xc+dx;
yc:=put(xc); {значение подынтегр. функции в серединной точке}
dy:= put(xi+dx) – put(xi); {приращение пути на частичном отрезке}
dl:=sqrt(dx*dx + dy*dy); {≈ длине дуги для частичного отрезка}
s:= s+ piv(xc,yc,dl)
xi:=xi+dx;
end;
writeln (n:6,tr:14:6,s:12:6,abs(s–tr):11:6,abs((s–tr)/tr):12:6);
readln;
readln;
end.
Окно вывода отлаженной программы должно иметь вид:
Введите число разбиений n
Р Е З У Л Ь Т А Т Ы
100 9.818743 9.818766 0.000023 0.000002
Отлаженную программу необходимо «запомнить» под своим оригинальным именем на своем компьютере и, что очень желательно (во избежание затирания программы другим пользователем), на дискете или на «флэшке».
Пример 2. Вычислить криволинейный интеграл  , где L –
, где L –
окружность r = a cos φ (a = 2).
program ivanov_kri1_2; {полярный}
Var
fi0,fin,dfi,dr,s,fii,fic,rc,dl,tr: real;
n,i: integer;
const a=2;
function piv(r,fi,dl: real): real; {подынтегральное выражение r dl }
Begin
piv:=r*dl;
end;
function put(fi: real): real; {кривая интегрирования acosφ}
Begin
put:= a*cos(fi);
end;
Begin
writeln (‘введите пределы интегрирования по фи: fi0 и fin’);
read (fi0,fin); {ввод fi0,fin }
{т.к. точное значение π/2 в паскале на «черном» экране ввести нельзя, то}
{‘перевводим’ пределы в программе, а требуемые значения вводим}
{ произвольно, например, 0, 0}
fi0:= –pi/2; fin:= pi/2;
tr:=2*a*a; (аналитическое решение)}
writeln (‘введите число разбиений n отрезка [fi0, fin]’);
read (n); {ввод n }
writeln (‘ Р Е З У Л Ь Т А Т Ы’);{впереди 20 пробелов}
writeln;
writeln (‘ n точн.знач. числ.реш. абс.ош. отн.ош’);{4,7,2,3,5 пробелов}
writeln;
dfi:=(fin–fi0)/n;
s:=0; {интегральная сумма}
fii:=fi0; {начальная точка частичных угловых интервалов}
fiс:=fi0–dfi/2; {серединная точка частичных угловых интервалов }
for i:=1 to n do
Begin
fiс:=fic+dfi;
rc:=put(fic); {значение подынтегр. функции в серединной точке}
dr:= put(fii+dfi) – put(fii); {приращение пути на угловом интервале }
dl:=sqrt(rc*dfi*rc*dfi+dr*dr); {≈длине дуги для частичного углового интервала}
s:= s+ piv(rc,fic,dl);
fii:=fii+dfi;
end;
writeln (n:6,tr:14:6,s:12:6,abs(s–tr):11:6,abs((s–tr)/tr):12:6);
readln;
readln;
end.
Окно вывода отлаженной программы должно иметь вид:
Введите число разбиений n
Р Е З У Л Ь Т А Т Ы
100 8.000000 8.000219 0.000219 0.000027
Пример 3. Вычислить криволинейный интеграл первого рода от функции трех переменных  , где L – дуга кривой, заданной параметрически x = t cos t, y = t sin t, z = t, 0 ≤ t ≤ π.
, где L – дуга кривой, заданной параметрически x = t cos t, y = t sin t, z = t, 0 ≤ t ≤ π.
program ivanov_kri1_3; {параметрическое задание кривой интегрирования}
Var
t0,tn,dt,dl,dx,dy,dz,s,ti,tc,xi,yi,zi,xi1,yi1,zi1,xc,yc,zc,u,tr: real;
n,i: integer;
function piv(x,y,z,dl: real): real; {подынтегральное выражение}
Begin
piv:=(5*z–2*sqrt(x*x+y*y))*dl;
end;
procedure put(t: real; var x,y,z:real); {кривая интегрирования}
Begin
x:= t*cos(t);
y:= t*sin(t);
z:= t;
end;
Begin
writeln (‘введите пределы интегрирования по t: t0 и tn’);
read (t0,tn); {ввод t0,tn }
{т.к. точное значение π в паскале на «черном» экране ввести нельзя, то}
{‘перевводим’ пределы в программе, а требуемые значения вводим}
{ произвольно, например, 0, 0}
t0:= 0;
tn:= pi;
tr:=sqrt((2+pi*pi)*(2+pi*pi)*(2+pi*pi))–2*sqrt(2); (аналитическое решение)}
writeln (‘введите число разбиений n отрезка [t0, tn]’);
read (n); {ввод n }
writeln (‘ Р Е З У Л Ь Т А Т Ы’); {впереди 13 пробелов}
writeln;
writeln (‘ n числ.реш.’); {5,7 пробелов}
writeln;
dt:=(tn–t0)/n;
s:=0; {интегральная сумма}
ti:=t0; {начальная точка частичных отрезков}
tс:=t0–dt/2; {серединная точка частичных отрезков }
for i:=1 to n do
Begin
tс:=tc+dt;
put(tc,xc,yc,zc); {значения подынтегр. функции в серединной точке отрезка}
put(ti,xi,yi,zi); {значения подынтегр. функции в начальной точке отрезка}
put(ti+dt,xi1,yi1,zi1); {значения подынтегр. функции в конечной точке отрезка}
dx:= xi1–xi;
dy:= yi1–yi;
dz:= zi1–zi;
dl:=sqrt(dx*dx+dy*dy+dz*dz); {≈длине дуги}
s:= s+ piv(xc,yc,zc,dl);
ti:=ti+dt;
end;
writeln (n:7, s:14:6);
writeln (‘аналитическое решение tr=’, tr:10:6);
writeln;
writeln (‘ошибка метода’);
writeln (‘абсолютная’, abs(s–tr):18:6);
writeln (‘относительная’, abs((s–tr)/tr):15:6);
readln;
readln;
end.
Окно вывода отлаженной программы должно иметь вид:
Р Е З У Л Ь Т А Т Ы
N числ.реш.
100 38.062661
аналитическое решение tr= 38.065081
Ошибка метода
Абсолютная 0.002420
Относительная 0.000064
Пример 4. Вычислить криволинейный интеграл 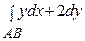 от точки
от точки
А (0; 0) до точки В (1; 1) по кривым а) у = х, б) у = х 2, в) у = 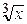 (см. рис.6).
(см. рис.6).
program ivanov_kri2_1; {по трем кривым АВС (рис.6)}
Var
a,b,dx,dy1,dy2,dy3,xi,xc,yc1,yc2,yc3,s1,s2,s3,tr1,tr2,tr3: real;
n,i: integer;
function piv(x,y,dx,dy: real): real; {подынтегральное выражение}
Begin
piv:= y*dx+2*dy;
end;
function put1(x: real): real; {кривая интегрирования y=x }
Begin
put1:= x;
end;
function put2(x: real): real; {кривая интегрирования y=x2}
Begin
put2:= x*x;
end;
function put3(y: real): real; {кривая интегрирования y=x1/3}
Begin
put3:= exp(ln(x)/3);
end;
Begin
{аналитическое решение}
tr1:=5/2; { по кривой y=x}
tr2:=7/3; { по кривой y=x2}
tr3:=11/4; { по кривой y= x1/3}
writeln (‘введите число разбиений n отрезка [0,1]’);
read (n); {ввод n }
writeln (‘n=’, n:5);
writeln (‘ Р Е З У Л Ь Т А Т Ы’);{впереди 20 пробелов}
writeln;
writeln (“:13,‘кривая y=x y=x*x y=e(ln(x)/3’);{5,10,6 пробелов}
writeln;
a:=0; {абсцисса точки А }
b:=1; {абсцисса точки B }
dx:=(b–a)/n;
s1:=0; {интегральная сумма для кривой y=x }
s2:=0; {интегральная сумма для кривой y=x*x }
s3:=0; {интегральная сумма для кривой y=e(ln(x)/3}
xi:=a; {начальная точка частичных отрезков}
xс:=xi–dx/2; {серединная точка частичных отрезков}
for i:=1 to n do
Begin
xс:=xc+dx;
yc1:=put1(xc); {знач. подынтегр. ф-ции в серединной точке для y=x }
yc2:=put2(xc); {знач. подынтегр. ф-ции в серединной точке для y=x*x }
yc3:=put3(xc); {зн. подынтегр. ф-ции в серединной точке для e(ln(x)/3 }
dy1:= put1(xi+dx) – put1(xi); {приращение пути для y=x}
dy2:= put2(xi+dx) – put2(xi); {приращение пути для y= x*x}
dy3:= put3(xi+dx) – put3(xi); {приращение пути для y= e(ln(x)/3}
s1:= s1+ piv(xc,yc1,dx,dy1);
s2:= s2+ piv(xc,yc2,dx,dy2);
s3:= s3+ piv(xc,yc3,dx,dy3);
xi:=xi+dx;
end;
writeln (‘численные’, s1:20:6, s2:14:6, s3:14:6);
writeln;
writeln (‘аналитические’, tr1:16:6, tr2:14:6, tr3:14:6);
readln;
readln;
end.
Окно вывода отлаженной программы должно иметь вид:
Введите число разбиений n
n= 100
Р Е З У Л Ь Т А Т Ы
кривая y=x y=x*x y=e(ln(x)/3)
Численные 2.500000 2.333325 2.750122
Аналитические 2.500000 2.333333 2.750000
Пример 5. Найти площадь области, ограниченной эллипсом
x = a cos t, y = b sin t.
Площадь S области D, ограниченной кривой L, находят по формуле
S = 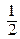
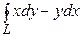 .
.
program petrov_kri2_2; {площадь эллипса}
Var
t0,tn,dt,dx,dy,ti,tc,xi,yi,xi1,yi1,xc,yc,s,tr: real;
n,i: integer;
const a=2;
const b=3;
function piv(x,y,dx,dy: real): real; {подынтегральное выражение}
Begin
piv:= x*dy–y*dx;
end;
procedure put (t: real; var x,y: real); {кривая интегрирования }
Begin
x:=a*cos(t);
y:=b*sin(t);
end;
Begin
tr:=pi*a*b; {аналитическое решение}
{пределы интегрирования t0, tn}
t0:=0;
tn:=2*pi;
write (‘введите число разбиений n =’);
read (n); {ввод n }
writeln;
writeln (‘ Р Е З У Л Ь Т А Т Ы’);{впереди 12 пробелов}
writeln;
writeln (‘ числ.реш. аналит.реш.’);{6,7 пробелов}
dt:=(tn–t0)/n;
s:=0; {интегральная сумма}
ti:=t0; {начальная точка частичных угловых отрезков}
tс:=t0–dt/2; {серединная точка частичных угловых отрезков}
for i:=1 to n do
Begin
tс:=tc+dt;
put (tc,xc,yc); {знач. x и y в серед. точке част. угловых отрезков }
put (ti,xi,yi); { знач. x и y в начальной точке част. угловых отрезков }
put (ti+dt,xi1,yi1); { знач. x и y в конечной точке част. угловых отрезков }
dx:= xi1–xi; {приращение x на част. угловом отрезке}
dy:= yi1–yi; {приращение y на част. угловом отрезке}
s:= s+ piv(xc,yc,dx,dy); {интегральная сумма}
ti:=ti+dt;
end;
s:=s/2;
writeln (s:15:6, tr:16:6);
writeln;
writeln (‘ошибка метода’);
writeln (‘абсолютная’, abs(s–tr):18:6);
writeln (‘относительная’, abs((s–tr)/tr):15:6);
readln;
readln;
end.
Окно вывода отлаженной программы должно иметь вид:
введите число разбиений n=100
Р Е З У Л Ь Т А Т Ы
Числ.реш. аналит.реш.
18.846455 18.849556
Ошибка метода
Абсолютная 0.003100
Относительная 0.000164
Четвертый этап работы заключается в записи в отлаженную
программу (в раздел описания функций) описания «своего» подынтегрального выражения (в предложенных выше программах это piv), «своей» кривой интегрирования (put) и «своего» аналитического решения (tr). После отладки программы ее необходимо «пропустить» со значениями n, равными 5, 10, 25, 100,1000.
При записи «своих» выражений следует обратить внимание на операцию деления. Например, правильная запись дроби 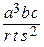 может иметь вид sqr(a)*a*b*c/(r*t*sqr(s)), или sqr(a)*a*b*c/ r / t / sqr(s), или a*a*a*b*c/(r*t*s*s), или какой-либо другой, но обязательно знаменатель должен быть в скобках или его множители должны быть отделены друг от друга операцией / (деление). Числитель брать в скобки нужно в случае, если это многочлен.
может иметь вид sqr(a)*a*b*c/(r*t*sqr(s)), или sqr(a)*a*b*c/ r / t / sqr(s), или a*a*a*b*c/(r*t*s*s), или какой-либо другой, но обязательно знаменатель должен быть в скобках или его множители должны быть отделены друг от друга операцией / (деление). Числитель брать в скобки нужно в случае, если это многочлен.
Другая особенность данного этапа состоит в ограниченности библиотеки встроенных функций PASCALя. Для записи встречающихся в заданиях функций используются функции
sin(x), cos(x), sqr t(x) (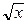 ), sqr(x) (x 2), atan(x) (arctg x), ln(x), abs(x) (| x|),
), sqr(x) (x 2), atan(x) (arctg x), ln(x), abs(x) (| x|),
а также постоянная pi (π).
Для записи других функций следует пользоваться тождественными формулами:
tg x = 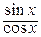 , arcsin x = arctg
, arcsin x = arctg 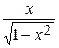 , xa = ea ln x ,
, xa = ea ln x ,
arcctg x = 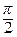 – arctg x, arccos x = arcctg
– arctg x, arccos x = arcctg 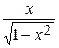 .
.
Еще два замечания:
1) Так как встроенная функция sqr(x) выполняется значительно дольше, чем операция * (умножение), то при возведении в целую степень при небольших значениях показателя степени желательно использовать операцию умножения.
2) Если в выражении функции некоторая степень встречается несколько раз, ее желательно вычислить один раз и в дальнейшем использовать вычисленное значение. Например, функцию y = x 5 + sin(x 5 + x 4 – x 3) можно описать так:
function primer (x: real): real;
y: real;
Begin
y:= x*x*x*x*x;
primer:= y+sin(y+y/x–y/x/x)
end;
Пятый этап представляет собой защиту работы.
При этом необходимо:
1. Знать определения криволинейных интегралов первого и второго рода,
методы аналитического и численного вычисления данных интегралов (в пределах данной методички).
2. Уметь объяснять полученные результаты, как-то, как и почему влияет на оценку интеграла число разбиений отрезка интегрирования.
3. Уметь объяснять функциональное назначение отдельных операторов и мест в программе.
4. Показать результаты аналитических расчетов в рабочей тетради.
5. При небольшом значении n вручную получить приближенное значение какого-нибудь простого криволинейного интеграла, предложенного преподавателем. Для этого может быть использован список таких заданий, предложенный в приложении 1. Желательно, чтобы интеграл в данном задании отличался по роду и виду интегральной функции от основного интеграла лабораторной работы. При выполнении этого задания можно пользоваться калькулятором или Mathcad’ом.
Примеры выполнения таких заданий представлен ниже.
Примеры выполнения задания ручного счета.
1. Вычислить вручную приближенное значение криволинейного интеграла 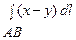 , где АВ – отрезок прямой у =
, где АВ – отрезок прямой у = 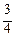 х от точки А (0, 0) до точки В (4, 3) при n = 4.
х от точки А (0, 0) до точки В (4, 3) при n = 4.
Так как, согласно определению, криволинейный интеграл первого рода (по длине дуги кривой) есть предел интегральных сумм вида
Sn = 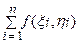 Δ li,
Δ li,
не зависящий ни от способа разбиения кривой АВ на частичные дуги, ни от выбора точек Ri (ξi, ηi), то для приближенного вычисления заданного в условии задачи интеграла построим интегральную сумму следующим образом:
1) разобьем кривую АВ на четыре (n = 4) частичных дуги так, чтобы их проекции на ось Ох ([ х 0; х 1], [ х 1; х 2], [ х 2; х 3], [ х 3; х 4]) равнялись между собой. В нашем случае х 0 = 0, х 4 = 4;
2) абсциссы точек Ri (ξi, ηi) (i = 1, 2, 3, 4), а именно ξi будем выбирать (согласно выбранному алгоритму) в серединах отрезков [ хi –1; хi ], а их ординаты ηi – это ординаты точек кривой АВ, соответствующие абсциссам ξi;
3) длину частичной дуги Δ li заменим длиной хорды, соединяющей конечные точки данной дуги: Δ li ≈ Δ si = 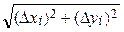 .
.
Разобьем отрезок [0; 4] (по х) на 4 равных частичных отрезка: [0; 1],
[1; 2], [2; 3], [3; 4]. При этом: х 0 = 0, х 1 = 1, х 2 = 2, х 3 = 3, х 4 = 4. Длина каждого из этих отрезков Δ х = Δ хi = хi – хi –1 = 1 (i = 1, 2, 3, 4). Подсчитаем значения у в граничных точках данных отрезков:
уi = 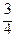 хi (i = 0, 1, 2, 3, 4): у 0 = 0, у 1 =
хi (i = 0, 1, 2, 3, 4): у 0 = 0, у 1 = 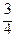 , у 2 =
, у 2 = 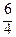 , у 3 =
, у 3 = 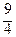 , у 4 =
, у 4 = 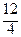 .
.
Приращение у на каждом i –м частичном отрезке (i = 1, 2, 3, 4) Δ уi = уi – уi –1 :
Δ у 1 = 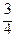 – 0 =
– 0 = 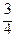 ; Δ у 2 =
; Δ у 2 = 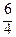 –
– 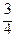 =
= 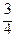 ; Δ у 3 =
; Δ у 3 = 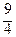 –
– 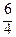 =
= 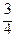 ; Δ у 4 =
; Δ у 4 = 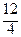 –
– 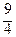 =
= 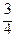 .
.
Срединные точки частичных интервалов ξi = xi *= 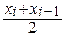 (i = 1, 2, 3, 4):
(i = 1, 2, 3, 4):
х 1* = 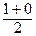 =
= 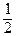 , х 2* =
, х 2* = 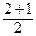 =
= 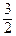 , х 3* =
, х 3* = 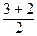 =
= 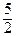 , х 4* =
, х 4* = 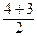 =
= 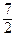 .
.
Значения у в этих срединных точках ηi = уi * = 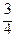 xi * (i = 1, 2, 3, 4):
xi * (i = 1, 2, 3, 4):
у 1* = 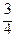 ∙
∙ 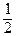 =
= 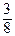 , у 2* =
, у 2* = 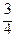 ∙
∙ 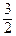 =
= 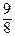 , у 3* =
, у 3* = 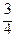 ∙
∙ 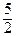 =
= 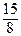 , у 4* =
, у 4* = 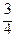 ∙
∙ 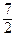 =
= 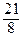 .
.
Полученные результаты сведем в таблицу
| i
| xi
| yi
= 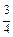 xi xi
| Δ хi
= хi – хi –1
| Δ yi
= yi – yi –1
| xi *
= 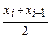
| уi *
= 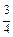 xi * xi *
| Δ si = 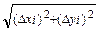
| f (xi *, уi *)
= xi * – уi *
| f (xi *, уi *)Δ si
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 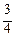
|
| 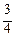
| 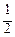
| 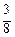
| 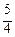
| 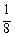
| 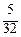
|
|
|
| 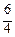
|
| 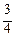
| 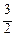
| 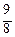
| 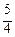
| 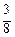
| 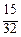
|
|
|
| 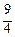
|
| 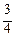
| 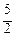
| 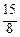
| 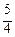
| 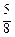
| 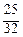
|
|
|
| 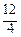
|
| 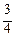
| 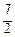
| 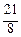
| 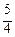
| 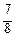
| 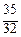
|
Таким образом, искомое приближенное значение криволинейного интеграла равно
I ≈ S 4 = f (х 1*, y 1*) ∙Δ s 1 + f (х 2*, y 2*) ∙Δ s 2 + f (х 3*, y 3*) ∙Δ s 3 + f (х 4*, y 4*) ∙Δ s 4 =
= 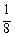 ∙
∙ 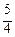 +
+ 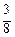 ∙
∙ 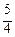 +
+ 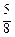 ∙
∙ 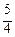 +
+ 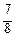 ∙
∙ 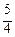 =
= 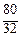 =
= 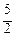 .
.
Точное значение интеграла
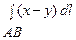 =
= 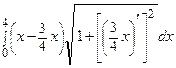 =
= 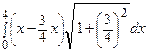 =
= 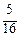
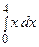 =
= 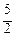 .
.
2. Вычислить вручную приближенное значение криволинейного интеграла 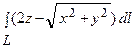 , где L – дуга кривой x = t cos t, y = t sin t, z = t, 0 ≤ t ≤ 2 π, при n = 4.
, где L – дуга кривой x = t cos t, y = t sin t, z = t, 0 ≤ t ≤ 2 π, при n = 4.
Разобьем кривую L на четыре (n = 4) частичных дуги Δ li (i = 1, 2, 3, 4) так, чтобы длины частичных интервалов [ t 0; t 1], [ t 1; t 2], [ t 2; t 3], [ t 3; t 4]) равнялись между собой.
Построим таблицу, содержащей следующие графы:
1. i – номер частичного интервала, на которые разбивается отрезок [0, 2 π ] (i = 1,
2, 3, 4);
2. ti – граничные точки частичных интервалов (i = 0, 1, 2, 3, 4). При этом: t 0 = 0,
t 4 = 2 π (отрезок [0, 2 π ] разбивается на 4 отрезка одинаковой длины);
3. xi = ti cos ti – значения функции x = t cos t в граничных точках частичных
интервалов (i = 0, 1, 2, 3, 4);
4. уi = ti sin ti – значения функции y = t sin t в граничных точках частичных
интервалов (i = 0, 1, 2, 3, 4);
5. zi = ti – значения функции z = t в граничных точках частичных интервалов
(i = 0, 1, 2, 3, 4);
6. Δ ti = ti – ti – 1– приращение параметра t на i – ом частичном интервале
(i = 1, 2, 3, 4). В соответствии с выбранным алгоритмом Δ ti = 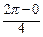 =
= 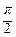 ;
;
7. Δ xi = xi – xi – 1– приращение функции х на i – ом частичном интервале;
8. Δ уi = уi – уi – 1– приращение функции у на i – ом частичном интервале;
9. Δ zi = zi – zi – 1– приращение функции z на i – ом частичном интервале;
10. Δ si = 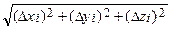 – длина хорды, соединяющей конечные точки
– длина хорды, соединяющей конечные точки
частичной дуги Δ li;
11. ti *= 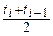 (i = 1, 2, 3, 4) – срединные точки частичных интервалов;
(i = 1, 2, 3, 4) – срединные точки частичных интервалов;
12. xi *= ti * cos ti * – значения функции x = t cos t в срединных точках частичных
интервалов (i = 1, 2, 3, 4);
13. yi *= ti * sin ti * – значения функции y = t sin t в срединных точках частичных
интервалов (i = 1, 2, 3, 4);
14. zi *= ti * – значения функции z = t в срединных точках частичных
интервалов (i = 1, 2, 3, 4);
15. fi *= f (xi *, yi *, zi *) = 2 zi – 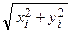 – значения подынтегральной функции в точках
– значения подынтегральной функции в точках
(xi, уi, zi).
| i
| ti
| xi
| yi
| zi
| Δ ti
| Δ xi
| Δ yi
| Δ zi
| Δ si
| ti *
| xi *
| yi *
| zi *
| fi *
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 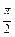
|
| 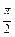
| 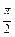
| 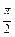
|
| 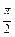
| 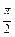
| π 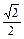
| 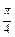
| 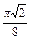
| 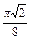
| 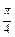
| 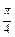
|
|
| π
| – π
|
| π
| 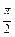
| – π
| – 
|
|
|
|



 x = x (t) и y = y (t) имеют на этом отрезке непрерывные производные x ¢(t) и y ¢(t), одновременно не равные нулю. Произвольно разобьем кривую L на n частей точками А = М 0, М 1, М 2, …, Мn = B. На каждой из полученных дуг Мi -1, Мi выберем произвольную точку Ri (ξi, ηi) (рис.1) и составим сумму
x = x (t) и y = y (t) имеют на этом отрезке непрерывные производные x ¢(t) и y ¢(t), одновременно не равные нулю. Произвольно разобьем кривую L на n частей точками А = М 0, М 1, М 2, …, Мn = B. На каждой из полученных дуг Мi -1, Мi выберем произвольную точку Ri (ξi, ηi) (рис.1) и составим сумму Δ li, (1)
Δ li, (1)










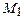
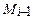




 кривой L. Пусть λ =
кривой L. Пусть λ =  Δ li - наибольшая
Δ li - наибольшая или
или 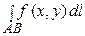 .
. [ a, b ], то
[ a, b ], то . (2)
. (2) . (3)
. (3) . (4)
. (4)
























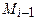
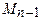



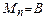 Sn =
Sn =  Δ xi + Q (ξi, ηi) Δ yi ] (2)
Δ xi + Q (ξi, ηi) Δ yi ] (2) + Q (x, y) dy или
+ Q (x, y) dy или  + Q (x, y) dy.
+ Q (x, y) dy. . (5)
. (5) . (6)
. (6) , где L –
, где L – , где L – дуга кривой, заданной параметрически x = t cos t, y = t sin t, z = t, 0 ≤ t ≤ π.
, где L – дуга кривой, заданной параметрически x = t cos t, y = t sin t, z = t, 0 ≤ t ≤ π.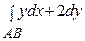 от точки
от точки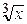 (см. рис.6).
(см. рис.6).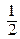
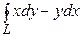 .
.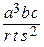 может иметь вид sqr(a)*a*b*c/(r*t*sqr(s)), или sqr(a)*a*b*c/ r / t / sqr(s), или a*a*a*b*c/(r*t*s*s), или какой-либо другой, но обязательно знаменатель должен быть в скобках или его множители должны быть отделены друг от друга операцией / (деление). Числитель брать в скобки нужно в случае, если это многочлен.
может иметь вид sqr(a)*a*b*c/(r*t*sqr(s)), или sqr(a)*a*b*c/ r / t / sqr(s), или a*a*a*b*c/(r*t*s*s), или какой-либо другой, но обязательно знаменатель должен быть в скобках или его множители должны быть отделены друг от друга операцией / (деление). Числитель брать в скобки нужно в случае, если это многочлен.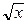 ), sqr(x) (x 2), atan(x) (arctg x), ln(x), abs(x) (| x|),
), sqr(x) (x 2), atan(x) (arctg x), ln(x), abs(x) (| x|),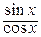 , arcsin x = arctg
, arcsin x = arctg 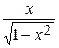 , xa = ea ln x ,
, xa = ea ln x ,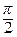 – arctg x, arccos x = arcctg
– arctg x, arccos x = arcctg 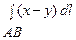 , где АВ – отрезок прямой у =
, где АВ – отрезок прямой у = 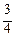 х от точки А (0, 0) до точки В (4, 3) при n = 4.
х от точки А (0, 0) до точки В (4, 3) при n = 4.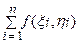 Δ li,
Δ li,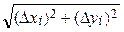 .
.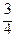 хi (i = 0, 1, 2, 3, 4): у 0 = 0, у 1 =
хi (i = 0, 1, 2, 3, 4): у 0 = 0, у 1 = 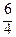 , у 3 =
, у 3 = 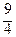 , у 4 =
, у 4 = 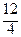 .
.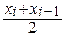 (i = 1, 2, 3, 4):
(i = 1, 2, 3, 4):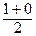 =
= 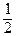 , х 2* =
, х 2* = 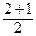 =
= 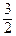 , х 3* =
, х 3* = 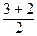 =
= 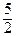 , х 4* =
, х 4* = 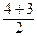 =
= 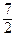 .
.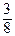 , у 2* =
, у 2* = 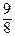 , у 3* =
, у 3* = 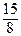 , у 4* =
, у 4* = 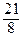 .
.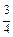 xi
xi
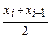
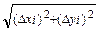
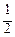
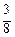
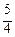
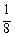
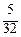
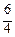
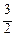
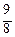
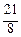
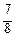
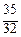
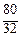 =
= 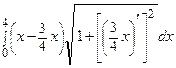 =
= 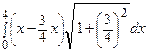 =
= 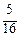
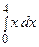 =
= 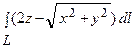 , где L – дуга кривой x = t cos t, y = t sin t, z = t, 0 ≤ t ≤ 2 π, при n = 4.
, где L – дуга кривой x = t cos t, y = t sin t, z = t, 0 ≤ t ≤ 2 π, при n = 4.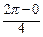 =
= 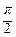 ;
;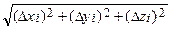 – длина хорды, соединяющей конечные точки
– длина хорды, соединяющей конечные точки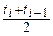 (i = 1, 2, 3, 4) – срединные точки частичных интервалов;
(i = 1, 2, 3, 4) – срединные точки частичных интервалов;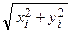 – значения подынтегральной функции в точках
– значения подынтегральной функции в точках