Цель работы: проверить справедливость второго закона Ньютона для движения тела по окружности под действием нескольких сил.
Оборудование, средства измерения: груз; нить; штатив с муфтой и кольцом; лист бумаги; измерительная лента; часы с секундной стрелкой.
Теоретическое обоснование:
Экспериментальная установка состоит из груза, привязанного на нити к кольцу штатива. На столе под маятником располагают лист бумаги, на котором нарисована окружность радиусом 10 см. Центр окружности находится на вертикали под точкой подвеса маятника. При движении груза по окружности, изображенной на листе, нить описывает коническую поверхность. Поэтому такой маятник называют коническим.

К
h a

X О R 
Y
 (рис.1)
(рис.1)
1. Центростремительное ускорение аn маятника, направленное к точке О, создается одновременным действием на него силы тяжести mg и силы натяжения нити Fn. Второй закон Ньютона для движения груза в векторной форме имеет вид
 (1) уравнение в проекциях на оси принимает вид
(1) уравнение в проекциях на оси принимает вид
(Х) man = Fn*Sina (2)
(Y) 0 = mg – Fn*Cosa,
где α- угол, образуемый нитью с вертикалью
Выразим Fn из последнего уравнения и подставим в уравнение (2). Тогда, an= g*tga (3)
Известно  . Период можно определить, измерив время t, за которое маятник совершает N оборотов: T = t/N, из рисунка видно tga = R/h, h – расстояние от точки подвеса до центра окружности О, радиуса R. Собрав в одну формулу (3) получим
. Период можно определить, измерив время t, за которое маятник совершает N оборотов: T = t/N, из рисунка видно tga = R/h, h – расстояние от точки подвеса до центра окружности О, радиуса R. Собрав в одну формулу (3) получим
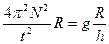 (4), формула (4) – прямое следствие второго закона Ньютона. Таким образом, первый способ проверки справедливости второго закона Ньютона сводится к экспериментальной проверке тождественности левой и правой части равенства.
(4), формула (4) – прямое следствие второго закона Ньютона. Таким образом, первый способ проверки справедливости второго закона Ньютона сводится к экспериментальной проверке тождественности левой и правой части равенства.
2. Второй способ основан на непосредственном измерении равнодействующей силы  силы тяжести
силы тяжести  и силы натяжения
и силы натяжения  :
: 
Сила  сообщает маятнику центростремительное ускорение аn= F/m. С учетом формул ускорения и периода второй закон Ньютона принимает вид
сообщает маятнику центростремительное ускорение аn= F/m. С учетом формул ускорения и периода второй закон Ньютона принимает вид
 (5), сила измеряется с помощью динамометра. Маятник оттягивают от положения равновесия на расстояние равное радиусу окружности R, и снимают показания динамометра. Масса груза считается известной.
(5), сила измеряется с помощью динамометра. Маятник оттягивают от положения равновесия на расстояние равное радиусу окружности R, и снимают показания динамометра. Масса груза считается известной.




 K
K
a 
 h
h







 О R
О R


 F (рис.2)
F (рис.2)
Следовательно, еще один способ проверки справедливости второго закона Ньютона, сводится к экспериментальной проверке тождественности левой и правой частей равенства (5). Так как у (4) и (5), левые части равенств равны, то можно сравнить выражения 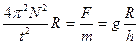
Порядок выполнения работы:
- Соберите экспериментальную установку по рис. 1, выбирая длину маятника около 50 см.
- На листе бумаги начертите окружность радиусом 10 см. (Погрешность измерения здесь DR =0,2 см.)
- Лист бумаги расположите так, чтобы центр окружности находился под точкой подвеса маятника по вертикали, чуть касаясь бумаги.
- Измерьте расстояние h между точкой подвеса К и центром окружности О сантиметровой лентой. h =
- Погрешность определите используя справочный материал. D h =
- Приведите в движение конический маятник вдоль начерченной окружности с постоянной скоростью. Измерьте время t, в течении которого маятник совершает 10 оборотов. t =.
- Определите абсолютную погрешность времени D t =
- Вычислите центростремительное ускорение груза – левую часть равенства (4)

- Рассчитайте относительную и абсолютную погрешности левой части равенства (4). Смотри справочный материал, как рассчитать погрешность косвенных измерений. ε =; DЛ4= Dаn =;
- Вычислите правую часть равенства (4) П4= gR/h=
- Рассчитайте относительную и абсолютную погрешности правой части ε =; D П4=
- Запишите результат измерения правой и левой частей равенства
Л4= Л4изм ± DЛ4 П4= П4изм ± D П4
- Сравните полученные результаты (см. справочный материал), сделай вывод
- Оттяните маятник от положения равновесия на расстояние равное радиусу окружности R, и определите показания динамометра. F =,
- при этом погрешность измерения силы определите используя справочный материал. D F=
- Вычислите правую часть формулы (5). При этом масса груза равна: m = m ±Dm = (100 ± 0,5) г П5=F/m =
- Рассчитайте относительную и абсолютную погрешности П5 (смотри пункт 7):
e = D П5 =
- Левые части равенств (4) и (5) равны то, DЛ4 = DЛ5
- Запишите результат измерения правой и левой частей равенства
Л5= Л5изм ± DЛ5 П5= П5изм ± D П5
- Сравните полученные результаты (см. справочный материал), сделай вывод
Вывод: ____________________________________________________________________________________________________________________________________________________________________________________________________________________________
Лабораторная работа № 5
Измерение коэффициента трения скольжения.
Цель работы: измерить коэффициент трения скольжения деревянного бруска по деревянной линейке двумя различными способами.
Оборудование, средства измерения: 1) деревянный брусок, 2) набор грузов, 3) динамометр, 4) деревянная линейка, 5) измерительная лента.
Теоретическое обоснование
1.Принципиальная схема первого способа измерения коэффициента трения скольжения приведен на рисунке 1.
Деревянный брусок, на котором сверху помещаются грузы, присоединен к динамометру.
При приложении к динамометру внешней силы брусок может перемещаться по горизонтально расположенной деревянной линейке. При равномерном движении бруска его ускорение равно нулю. Согласно второму закону Ньютона, геометрическая сумма сил действующих на брусок в этом случае, равна нулю. Это означает, что сила трения скольжения уравновешивает силу растяжения пружины динамометра и может быть измерена динамометром.
Коэффициент трения скольжения определяется как коэффициент пропорциональности между силой трения Fтр и силой нормального давления бруска F┴ с грузами на опору (или весом тела), то есть остается постоянным:  Fтр= μ F┴. (1)
Fтр= μ F┴. (1)
Сила нормального давления F┴ в данном случае равна весу бруска вместе с грузом и определяется взвешиванием с помощью динамометра. Тогда по результатам измерений Fтр и F┴ можно вычислить коэффициент трения скольжения:  (2)
(2)
Согласно формуле (1) графиком зависимости Fтр от силы нормального давления F┴ является прямая линия (рис 2). Как видно из графика, μ = tgα (где α – угол наклона прямой к оси абсцисс).


 N
N
 Fтр
Fтр 









 L Fтр
L Fтр

 α α h
α α h

 α α mg
α α mg



 0 F┴ X a Y
0 F┴ X a Y
 Рис. 2 рис. 3
Рис. 2 рис. 3
Второй способ измерения коэффициента трения скольжения не требует непосредственного измерения сил и соответственно использования динамометра. В этом случае один из концов линейки с помещенным на него бруском и грузом постепенно приподнимают до тех пор, пока при небольшом толчке брусок не начинает равномерно скользить вниз равномерно по линейке (рис. 3). В этот момент линейка образует угол α с горизонталью, а сумма сил на оси Х и У, действующих на тело, будет равна нулю:
(Х) mg Sin α - Fтр = 0,
(Y) mg Cos α – N = 0. (3)
Учитывая, что Fтр = μ F┴, а F┴ = N по третьему закону Ньютона, можно представить систему уравнений (3) в виде
 mg Sin α = μN,
mg Sin α = μN,
mg Cos α = N. (4)
беря отношения правых и левых частей системы получаем; μ = tg α.
Как видно из рисунка 3  а следовательно
а следовательно  (5)
(5)
Ход работы.
1. С помощью динамометра определите вес деревянного бруска Р0, бруска вместе с одним грузом (Р0 + Р), бруска с двумя грузами (Р0 + 2Р), бруска с тремя грузами (Р0 + 3Р). Результаты занесите в табл. 1 (в графу F┴). (Почему?)
|
| Р0
| Р0 + Р
| Р0 + 2Р
| Р0 + 3Р
|
| F┴
|
|
|
|
|
| Fтр
|
|
|
|
|
2.  Динамометром равномерно тяните брусок по линейке, измеряя силу тяги Fт (Fт = Fтр). Опыт повторите, нагрузив брусок одним, потом двумя и тремя грузами. Результаты измерений Fтр запишите в таблицу 1. Fтр, Н
Динамометром равномерно тяните брусок по линейке, измеряя силу тяги Fт (Fт = Fтр). Опыт повторите, нагрузив брусок одним, потом двумя и тремя грузами. Результаты измерений Fтр запишите в таблицу 1. Fтр, Н
3. Постройте график зависимости Fтр(F┴) (рис. 4), используя
данные табл.1. Через начало отсчета проведите
прямую линию так, чтобы число точек над прямой (рис. 4)
равнялось числу точек под прямой.
0 F┴, Н
(Масштаб взять необходимо как можно больше) (Выберите сами удобный масштаб для построения графика).
4. Найдите коэффициент трения скольжения μ по формуле (5) как тангенс угла наклона прямой линии к ос абсцисс. (Тангенс, это отношение …!!!)
Для этого выберите произвольную точку с координатами (F┴, Fтр) на прямой и найдите μ как отношение  . (а это и есть тангенс угла наклона)
. (а это и есть тангенс угла наклона)
5. Через начало отсчета проведите прямую линию под минимальным углом наклона к горизонтали через экспериментальную точку. Рассчитайте минимальное значение коэффициента трения скольжения. μmin = tg αmin =
6. Оцените абсолютную погрешность измерения коэффициента трения скольжения.
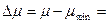
!!! Если все точки лежат на одной прямой графика, найдите табличное значение коэффициента трения и оцените погрешность измерения. (Смотри справочный материал).(Это бывает если масштаб берется малым).
7. Запишите окончательный результат: μ1 ± Δμ1 =
Второй способ определения коэффициента трения.
1. Измерьте длину линейки l = (Пусть Δl = 1см).
2. На один из концов линейки поместите брусок с одним грузом и медленно приподнимите его (см. рис. 3). Измерьте высоту подъема h конца линейки, когда при небольшом толчке брусок начинает скользить вниз равномерно: h =… (пусть Δh = 1 см)
3. Вычислите коэффициент трения по формуле (5). μ = …
5. Рассчитайте относительную погрешность косвенного измерения коэффициента трения скольжения по формуле 
6. Вычислите абсолютную погрешность косвенного измерения коэффициента трения скольжения Δμ =
7. Запишите окончательный результат.
μ2 ± Δμ2 =
8. Сравните величины коэффициента трения скольжения, измеренные двумя различными способами. (См. справочный материал.)
9. Вывод:____________________________________________________________________________________________________________________________________________________________________________________________________________________
Дополнительное задание: Доказать, что сила трения не зависит от площади трущихся поверхностей.
1. Деревянный брусок равномерно тяните динамометром по горизонтальной линейке, измеряя силу тяги.
2. Опыт повторите при перестановке бруска на другие грани с различной площадью поверхности.
3. Убедитесь, что сила трения скольжения не зависит от площади трущихся поверхностей, сделайте вывод.
Вывод:___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
(Дополнительная работа) Лабораторная работа «Измерение жесткости пружины»
Цель работы: найти жесткость пружины.
Материалы: 1) штатив с муфтами и лапкой; 2) спиральная пружина; 3) набор грузов известной массы.
Порядок выполнения работы:
1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой - указателем и крючком).
2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.
3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины х0 =.
4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины х1 = х – х0.
5. Рассчитайте силу упругости при подвешивании первого груза, она равна силе тяжести Fупр = Fт = mg
6. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение /х/ пружины и силу упругости. По результатам измерений заполните таблицу (рис. 59):
| Номер опыта
| т,
кг
| тg
Н
| Х1 м
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7. По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины kср.
(Масштаб взять необходимо как можно больше) (Выберите сами удобный масштаб для построения графика).
8. Найдите жесткость пружины по формуле как тангенс угла наклона прямой линии к ос абсцисс. (Тангенс, это отношение …!!!)
Для этого выберите произвольную точку с координатами (mg, x) на прямой и найдите k как отношение  . (а это и есть тангенс угла наклона)
. (а это и есть тангенс угла наклона)
9. Через начало отсчета проведите прямую линию под минимальным углом наклона к горизонтали через экспериментальную точку. Рассчитайте минимальное значение;жесткости. kmin = tg αmin =
10. Оцените абсолютную погрешность измерения жесткости.

!!! Если все точки лежат на одной прямой графика, найдите табличное значение жесткости и оцените погрешность измерения. (Смотри справочный материал).(Это бывает если масштаб берется малым).
11.Запишите окончательный результат: k1 ± Δk1 =
Лабораторная работа № 6
Проверка закона сохранения энергии при действии сил тяжести и упругости.
Цель работы: измерить максимальную скорость тела, колеблющегося на пружине, с использованием закона сохранения энергии.
Оборудование, средства измерения: 1) динамометр, 2) штатив лабораторный, 3) груз массой 100 г – 2 шт., 4) измерительная линейка,
Теоретическое обоснование.
Схема экспериментальной установки приведена на рисунке 1.
Динамометр укреплен вертикально в лапке штатива. При подвешивании к динамометру грузов растяжение пружины определяется положением указателя. При этом максимальное удлинение (или статическое смещение) пружины х0 возникает тогда, когда сила упругости пружины с жесткостью k уравновешивает силу тяжести груза массой m: kx0 = mg, (1) где g = 9,81 м/с2 – ускорение свободного падения.
Следовательно,  (2)
(2)
Статическое смещение характеризует новое положение равновесия О’ нижнего конца пружины (рис. 2).


 Х
Х




 0
0





 2 х0
2 х0
 А
А



 О’
О’
А

 1
1
(рис.1) (рис.2)
Если груз оттянуть вниз на расстояние А от точки О’ и отпустить в точке 1, то возникают периодические колебания груза. В точках 1 и 2, называемых точками поворота, груз останавливается, изменяя направление движения на противоположное. Поэтому в этих точках скорость груза равна 0.
Максимальной скоростью vmax груз будет обладать в средней точке О’. На колеблющейся груз действуют две силы: постоянная сила тяжести mg и переменная сила kx, Потенциальная энергия тела в поле силы тяжести в произвольной точке с координатой х равна mgх. Потенциальная энергия деформированного тела соответственно равна 
При этом за нуль отсчета потенциальной энергии для обеих сил принята точка х = 0, соответствующая положению указателя для нерастянутой пружины.
Полная механическая энергия груза в произвольной точке складывается из его потенциальной и кинетической энергии. Пренебрегая силами трения, воспользуемся законом сохранения полной механической энергии.
Приравняем полную механическую энергию груза в точке 2 с координатой – (х0 – А) и полную механическую энергию груза в точке О’ с координатой (х0):
Wт2 + Wу2 + Wк2 = WтО + WуО + WкО
 (3)
(3)
Раскрывая и делая преобразования выражения (3), получаем формулу  (4)
(4)
Тогда модуль максимальной скорости грузов  (5)
(5)
Жесткость пружины можно найти, измерив статическое смещение х0. Как следует из формулы (1) 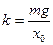 . Соответственно
. Соответственно  (7).
(7).
Порядок выполнения работы:
1. Соберите экспериментальную установку (см. рис. 1).
2. Измерьте линейкой статическое смещение пружины (новое положение равновесия нижнего конца пружины динамометра) при подвешивании груза. Х0 =, Δх =
3. Оттяните груз вниз на 5 – 6 см от нового положения равновесия, это будет амплитуда колебания А. Измерьте амплитуду колебания А =, ΔА =
4. Рассчитайте модуль максимальной скорости колеблющегося груза по формуле (7)
vmax =; вычислите относительную погрешность ε =; рассчитайте абсолютную погрешность измерения скорости Δ vmax = (См. справочный материал).
Запишите окончательный результат.
Дополнительное задание: Измерьте период колебания тела на пружине и определите его максимальную скорость.
Как известно, период колебания пружинного маятника связан с его массой и жесткостью по закону 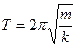 . Максимальная скорость колебаний равна (из закона сохранения энергии)
. Максимальная скорость колебаний равна (из закона сохранения энергии)  , а период колебания можно определить как
, а период колебания можно определить как  , с учетом этих формул можно получить
, с учетом этих формул можно получить 
Измерьте амплитуду колебаний А и время t десяти колебаний (N =10) маятника и рассчитайте модуль максимальной скорости груза. (при измерении колебаний разверните указатель динамометра, чтобы он имел меньшую силу трения, совершая колебания вдоль шкалы).
Vmax=
Сравните результат с полученным ранее другим способом. (Обратись к справочному материалу).
Вывод:____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________








 (рис.1)
(рис.1) (1) уравнение в проекциях на оси принимает вид
(1) уравнение в проекциях на оси принимает вид . Период можно определить, измерив время t, за которое маятник совершает N оборотов: T = t/N, из рисунка видно tga = R/h, h – расстояние от точки подвеса до центра окружности О, радиуса R. Собрав в одну формулу (3) получим
. Период можно определить, измерив время t, за которое маятник совершает N оборотов: T = t/N, из рисунка видно tga = R/h, h – расстояние от точки подвеса до центра окружности О, радиуса R. Собрав в одну формулу (3) получим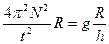 (4), формула (4) – прямое следствие второго закона Ньютона. Таким образом, первый способ проверки справедливости второго закона Ньютона сводится к экспериментальной проверке тождественности левой и правой части равенства.
(4), формула (4) – прямое следствие второго закона Ньютона. Таким образом, первый способ проверки справедливости второго закона Ньютона сводится к экспериментальной проверке тождественности левой и правой части равенства.
 (5), сила измеряется с помощью динамометра. Маятник оттягивают от положения равновесия на расстояние равное радиусу окружности R, и снимают показания динамометра. Масса груза считается известной.
(5), сила измеряется с помощью динамометра. Маятник оттягивают от положения равновесия на расстояние равное радиусу окружности R, и снимают показания динамометра. Масса груза считается известной.



 K
K
 h
h





 О R
О R
 F (рис.2)
F (рис.2)
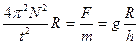


 Fтр= μ F┴. (1)
Fтр= μ F┴. (1) (2)
(2)

 N
N Fтр
Fтр 









 L Fтр
L Fтр



 α α h
α α h
 α α mg
α α mg

 0 F┴ X a Y
0 F┴ X a Y Рис. 2 рис. 3
Рис. 2 рис. 3 mg Sin α = μN,
mg Sin α = μN, а следовательно
а следовательно  (5)
(5) Динамометром равномерно тяните брусок по линейке, измеряя силу тяги Fт (Fт = Fтр). Опыт повторите, нагрузив брусок одним, потом двумя и тремя грузами. Результаты измерений Fтр запишите в таблицу 1. Fтр, Н
Динамометром равномерно тяните брусок по линейке, измеряя силу тяги Fт (Fт = Fтр). Опыт повторите, нагрузив брусок одним, потом двумя и тремя грузами. Результаты измерений Fтр запишите в таблицу 1. Fтр, Н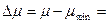

 . (а это и есть тангенс угла наклона)
. (а это и есть тангенс угла наклона)
 (2)
(2)

 Х
Х



 0
0




 2 х0
2 х0
 А
А


 О’
О’
 1
1
 (3)
(3) (4)
(4) (5)
(5)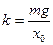 . Соответственно
. Соответственно  (7).
(7).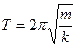 . Максимальная скорость колебаний равна (из закона сохранения энергии)
. Максимальная скорость колебаний равна (из закона сохранения энергии)  , а период колебания можно определить как
, а период колебания можно определить как  , с учетом этих формул можно получить
, с учетом этих формул можно получить 



