

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...
Топ:
Основы обеспечения единства измерений: Обеспечение единства измерений - деятельность метрологических служб, направленная на достижение...
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Интересное:
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Вопросы
1. Определение векторного произведения векторов.
2. Свойства векторного произведения.
3. Чему равен модуль векторного произведения.
4. Какая тройка векторов называется правой, левой.
5. Как найти площадь параллелограмма, построенного на векторах.
6. Формула для нахождения векторного произведения.
7. Определение смешанного произведения векторов.
8. Свойства смешанного произведения.
9. Чему равен модуль смешанного произведения.
10. Как найти объем параллелепипеда, построенного на векторах.
11. Как найти объем треугольной призмы, построенной на векторах.
Задачи
71. Найти векторное произведение  и
и  , заданных своими координатами:
, заданных своими координатами:
а)  ,
,  ,
,
б)  ,
,  ,
,
в) 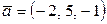 ,
,  .
.
72. Найти векторное произведение  и
и  , заданных в виде разложения по ортам координатных осей:
, заданных в виде разложения по ортам координатных осей:
а)  ,
,  ,
,
б)  ,
,  ,
,
в)  ,
,  .
.
73. Проверить, будут ли векторы  и
и  коллинеарными:
коллинеарными:
а)  ,
,  ,
,
б)  ,
,  ,
,
в)  ,
,  .
.
74. Найти объем параллелограмма, построенного на векторах  и
и  :
:
а)  ,
,  ,
,
б)  ,
,  ,
,
в)  ,
,  .
.
75. Найти смешанное произведение векторов  ,
,  и
и  , заданных своими координатами:
, заданных своими координатами:
а)  ,
,  ,
, 
б)  ,
,  ,
, 
в) 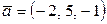 ,
,  ,
,  .
.
76. Найти смешанное произведение векторов  ,
,  и
и  , заданных в виде разложения по ортам координатных осей:
, заданных в виде разложения по ортам координатных осей:
а)  ,
,  ,
,  ;
;
б)  ,
,  ,
,  ;
;
в)  ,
,  ,
,  .
.
77. Проверить, будут ли векторы  ,
,  и
и  компланарными:
компланарными:
а)  ,
,  ,
,  ;
;
б)  ,
,  ,
, 
в)  ,
,  ,
,  .
.
78. Проверить, будут ли векторы  ,
,  и
и  линейно зависимыми:
линейно зависимыми:
а)  ,
,  ,
,  ;
;
б)  ,
,  ,
, 
в)  ,
,  ,
,  ;
;
г)  ,
,  ,
,  ;
;
79. Найти объем параллелепипеда, построенного на векторах  ,
,  и
и  :
:
а)  ,
,  ,
,  ;
;
б)  ,
,  ,
,  ;
;
в)  ,
,  ,
,  .
.
80. Найти объем треугольной призмы, построенной на векторах  ,
,  и
и  :
:
а)  ,
,  ,
, 
б)  ,
,  ,
, 
в)  ,
,  ,
,  .
.
81. Известно значение смешанного произведения векторов  ,
,  и
и  :
:
а)  , найти
, найти  ; б)
; б)  , найти
, найти 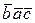 ;
;
в)  , найти
, найти 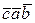 ; г)
; г)  , найти
, найти  ;
;
д) 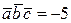 , найти
, найти  .
.
ЛИННИИ НА ПЛОСКОСТИ
ПРЯМАЯ НА ПЛОСКОСТИ
Прямая – это линия на плоскости, точки которой  удовлетворяют уравнению:
удовлетворяют уравнению:
|
|
 . (1)
. (1)
Коэффициент  называется угловым коэффициентом прямой. Он равен тангенсу угла наклона прямой к положительному направлению оси ОХ (рис.1). Коэффициент b равен координате точки, в которой прямая пересекает ось ОY.
называется угловым коэффициентом прямой. Он равен тангенсу угла наклона прямой к положительному направлению оси ОХ (рис.1). Коэффициент b равен координате точки, в которой прямая пересекает ось ОY.

Рис 1.
Помимо уравнения (1) – уравнения прямой с угловым коэффициентом, существуют другие уравнения прямой.
Уравнение прямой с угловым коэффициентом k, проходящей через данную точку 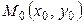 (рис 2.) имеет вид:
(рис 2.) имеет вид:
 . (2)
. (2)

Рис 2.
Уравнение прямой, проходящей через две данные точки  и
и  (рис 3.) имеет вид:
(рис 3.) имеет вид:
 . (3)
. (3)

Рис 3.
Уравнение прямой, проходящей через данную точку 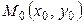 , параллельно данному вектору
, параллельно данному вектору 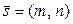 (рис 4.) имеет вид:
(рис 4.) имеет вид:
 . (4)
. (4)

Рис 4.
Уравнение прямой, проходящей через данную точку 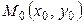 , перпендикулярно данному вектору
, перпендикулярно данному вектору  (рис 5.) имеет вид:
(рис 5.) имеет вид:
 . (5)
. (5)

Рис.5
Уравнение прямой в отрезках (рис 6.) имеет вид:
 . (6)
. (6)

Рис 6.
Общее уравнение прямой имеет вид:
 . (7)
. (7)
Замечание:
Все уравнения прямой могут быть приведены к общему уравнению прямой.
Расстояние от точки 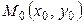 до прямой
до прямой  , заданной общим уравнением находится по формуле:
, заданной общим уравнением находится по формуле:
 . (8)
. (8)
СЕМИНАР 11.
ПРЯМАЯ НА ПЛОСКОСТИ
Вопросы
1. Уравнение прямой на плоскости с угловым коэффициентом.
2. Уравнение прямой с угловым коэффициентом, проходящей через данную точку.
3.Уравнение прямой, проходящей через две данные точки.
4. Уравнение прямой, проходящей через данную точку параллельно данному вектору.
5. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.
6. Уравнение прямой в отрезках.
7. Общее уравнение прямой.
8. Расстояние от точки до прямой.
Задачи
82. Для прямых, заданных на рисунках 1- 6, записать общее уравнение прямой на плоскости. Найти координаты нормального вектора.

 .
.
Рис.1 Рис.2


Рис. 3 Рис.4


Рис.5 Рис.6
83. Для прямых, заданных на рисунках 7- 12, записать уравнение прямой на плоскости в виде  . Найти угловой коэффициент и точку пересечения прямой с осью ОY.
. Найти угловой коэффициент и точку пересечения прямой с осью ОY.
|
|

 .
.
Рис.7 Рис.8


Рис. 9 Рис.10

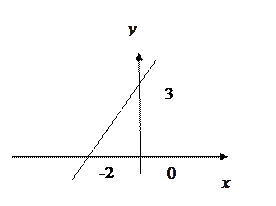
Рис.11 Рис.12
84.Точки P, Q и R являются вершинами треугольника.
Найти уравнение высоты РН.
а) Р(2, 3), Q(6, 2), Н(5, 6);
б) Р(2, 5), Q(-2, 2), Н(2, 1);
в) Р(-4, -1), Q(-4, -2), Н(-2, 2);
г) Р(3, -4), Q(2, -1), Н(1, -3).
85. Найти расстояние от точки М до прямой k.
а) М(1, 2), k:  ;
;
б) М(-8, 4), k:  ;
;
в) М(-3, -5), k:  ;
;
г) М(0, -2), k:  .
.
КРИВЫЕ ВТОРОГО ПОРЯДКА
Общее уравнение кривой второго порядка на плоскости имеет вид:
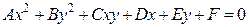 (9)
(9)
Окружностью называется кривая, точки которой находятся на равном расстоянии от некоторой заданной точки  – центра окружности (рис 7).
– центра окружности (рис 7).

Рис. 7
Каноническое уравнение окружности имеет вид:
 . (10)
. (10)
Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух заданных точек  и
и  – фокусов, есть величина постоянная (рис. 8).
– фокусов, есть величина постоянная (рис. 8).

Рис. 8
Каноническое уравнение эллипса имеет вид:
 . (11)
. (11)
F1 = (c; 0); F2(-c; 0), с – половина расстояния между фокусами; величина a – большая (действительная) полуось эллипса, b – малая (мнимая) полуось. Фокусное расстояние и полуоси эллипса связаны соотношением: a2 = b2 + c2.
Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом.

Так как с < a, то е < 1.
Если центр симметрии эллипса находится не в точке  , а в точке
, а в точке  , то каноническое уравнение эллипса приобретает вид:
, то каноническое уравнение эллипса приобретает вид:
 . (12)
. (12)
Гиперболой называется геометрическое место точек, абсолютная величина разности расстояний от которых до двух заданных точек  и
и  – фокусов, есть величина постоянная (рис. 9).
– фокусов, есть величина постоянная (рис. 9).
Каноническое уравнение гиперболы имеет вид:
 . (13)
. (13)
Здесь величина a – большая (действительная) полуось гиперболы, b – малая (мнимая) полуось.
 y
y
M(x, y)
b
r1
r2
x
F1 a F2
c
Рис 9.
Если центр гиперболы находится не в точке  , а в точке
, а в точке  , то каноническое уравнение гиперболы приобретает вид:
, то каноническое уравнение гиперболы приобретает вид:
 . (13)
. (13)
Если ветви гиперболы вытянуты не вдоль оси ОХ (действительной оси), а вдоль оси OY (мнимой оси), то каноническое уравнение гиперболы приобретает вид:
 . (14)
. (14)
Гипербола имеет две асимптоты, уравнения которых 
Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/e от него, называются директрисами гиперболы. Их уравнения: 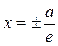 .
.
Отношение  называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.
называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.
|
|
Параболой называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.
Расположим начало координат посередине между фокусом и директрисой.
у

 а М(х, у)
а М(х, у)
 |
О F x
 |
p/2 p/2
Каноническое уравнение параболы имеет вид:
 . (15)
. (15)
Величина р (расстояние от фокуса до директрисы) называется параметром параболы.
Уравнение директрисы: x = -p /2.
Если вершина параболы находится не в точке  , а в точке
, а в точке  , то каноническое уравнение параболы приобретает вид:
, то каноническое уравнение параболы приобретает вид:
 (16)
(16)
Пример. На параболе у 2 = 8 х найти точку, расстояние которой от директрисы равно 4.
Из уравнения параболы получаем, что р = 4.
r = x + p/ 2= 4; следовательно:
x = 2; y2 = 16; y = ±4. Искомые точки: M1 (2; 4), M2 (2; -4).
СЕМИНАР 11.
КРИВЫЕ ВТОРОГО ПОРЯДКА
Вопросы
1. Общее уравнение кривой второго порядка.
2. Какая кривая называется окружностью.
3. Уравнение окружности.
4. Какая кривая называется эллипсом.
5. Действительная и мнимая полуось эллипса.
6. Экцентриситет эллипса.
7. Уравнение эллипса с центром в начале координат.
8. Уравнение эллипса со смещенным центром.
9. Какая кривая называется гиперболой.
10. Действительная и мнимая полуось гиперболы.
11. Директрисы гиперболы.
12. Уравнение гиперболы с центром в начале координат.
13. Уравнение гиперболы со смещенным центром.
14. Какая кривая называется параболой.
15. Директриса параболы.
16. Уравнение параболы с центром в начале координат.
17. Уравнение параболы со смещенным центром.
Задачи
86. Построить окружность, заданную уравнением:
а)  , б)
, б)  ,
,
в)  , г)
, г)  ,
,
д)  , е)
, е)  .
.
87. Определить центр и радиус окружности, заданной своим общим уравнением. Построить окружность.
а)  , б)
, б)  ,
,
в)  , г)
, г)  ,
,
д)  , е)
, е)  .
.
88. Построить эллипс, заданный своим каноническим уравнением
а)  , б)
, б)  ,
,
в)  , г)
, г)  ,
,
д)  , е)
, е) 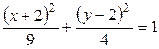 .
.
90.Определить центр, действительную и мнимую полуось эллипса, заданного своим общим уравнением. Построить эллипс.
а)  , б)
, б)  ,
,
в)  , г)
, г)  ,
,
д)  , е)
, е)  .
.
91. Построить гиперболу, заданную своим каноническим уравнением
а)  , б)
, б)  ,
,
|
|
в)  , г)
, г)  ,
,
д)  , е)
, е) 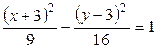 .
.
92.Записать каноническое уравнение гиперболы, заданной своим общим уравнением. Построить гиперболу.
а)  , б)
, б) 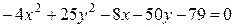 ,
,
в)  , г)
, г) 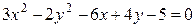 ,
,
д)  , е)
, е)  .
.
93. Построить параболу, заданную своим каноническим уравнением
а)  , б)
, б) 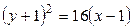 ,
,
в)  , г)
, г) 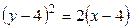 ,
,
д) 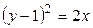 , е)
, е)  .
.
94.Записать каноническое уравнение параболы, заданной своим общим уравнением. Построить параболу.
а)  , б)
, б)  ,
,
в)  , г)
, г)  ,
,
д)  , е)
, е)  .
.
95. Определить, какая кривая 2-ого порядка задана своим общим уравнением. Записать каноническое уравнение. Построить кривую.
а)  , б)
, б) 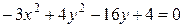 ,
,
в)  , г)
, г)  ,
,
д)  , е)
, е)  ,
,
ж)  , з)
, з)  ,
,
и)  , к)
, к)  ,
,
л)  , м)
, м)  ,
,
н)  .
.
9. ПРЯМЫЕ И ПЛОСКИСТИ В 
Плоскостью называется поверхность, все точки которой удовлетворяют общему уравнению:
Ax + By + Cz + D = 0,
где А, В, С – координаты вектора  – вектор нормали к плоскости, т. е. вектор, перпендикулярный плоскости.
– вектор нормали к плоскости, т. е. вектор, перпендикулярный плоскости.
Возможны следующие частные случаи:
А = 0 – плоскость параллельна оси Ох;
В = 0 – плоскость параллельна оси Оу;
С = 0 – плоскость параллельна оси Оz;
D = 0 – плоскость проходит через начало координат;
А = В = 0 – плоскость параллельна плоскости хОу
А = С = 0 – плоскость параллельна плоскости хОz
В = С = 0 – плоскость параллельна плоскости yOz
А = D = 0 – плоскость проходит через ось Ох
В = D = 0 – плоскость проходит через ось Оу
С = D = 0 – плоскость проходит через ось Oz
А = В = D = 0 – плоскость совпадает с плоскостью хОу
А = С = D = 0 – плоскость совпадает с плоскостью xOz
В = С = D = 0 – плоскость совпадает с плоскостью yOz
Уравнение плоскости, проходящей через данную точку, перпендикулярно данному вектору имеет вид:

Здесь вектор  – нормаль к плоскости Р; точка
– нормаль к плоскости Р; точка  – точка, через которую проходит плоскость Р.
– точка, через которую проходит плоскость Р.
Этот факт вытекает из рассуждений.
Для произвольной точки М(х, у, z), принадлежащей плоскости, составим вектор  . Т.к. вектор
. Т.к. вектор  - вектор нормали, то он перпендикулярен плоскости, а, следовательно, перпендикулярен и вектору
- вектор нормали, то он перпендикулярен плоскости, а, следовательно, перпендикулярен и вектору 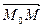 . Тогда скалярное произведение
. Тогда скалярное произведение
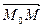 ×
×  = 0
= 0
Таким образом, получаем уравнение плоскости
 .
.
Если раскрыть скобки и сделать обозначение  , то получим общее уравнение плоскости:
, то получим общее уравнение плоскости:
 Чтобы узнать, принадлежит ли точка М(х,у,z) плоскости Р, необходимо подставить ее координаты в уравнение плоскости и убедится, что получилось истинное равенство.
Чтобы узнать, принадлежит ли точка М(х,у,z) плоскости Р, необходимо подставить ее координаты в уравнение плоскости и убедится, что получилось истинное равенство.
Пример: Плоскость Р задана своим общим уравнением.
 .Проверить, будут ли принадлежать плоскости Р точки
.Проверить, будут ли принадлежать плоскости Р точки  и
и  .
.
Подставим в заданное уравнение координаты точки L.
 , следовательно
, следовательно  .
.
Подставим в заданное уравнение координаты точки K.
 , следовательно
, следовательно  .
.
|
|
|

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!