| Уровень варьируемых факторов
| Кодированные обозначения
| Натуральные значения
факторов
|
|
|
| Д, мм (x 1)
| Р, МПа (x 2)
|
| Верхний уровень
| +
|
| 10,0
|
| Нижний уровень
| -
|
| 5,5
|
| Основной уровень
|
|
| 7,75
|
| Интервал
варьирования
| И
|
| 2,25
|
В табл. 2 верхний уровень соответствует нижней строке табл. 1, нижний – верхней строке.
После выбора параметра оптимизации, факторов и уровней их варьирования выполняем кодирование, перевод натуральных значений фактора в безразмерные, которое представляет собой линейное преобразование факторного пространства с переносом начала координат в нулевую точку плана эксперимента и выбор масштаба по осям в единицах интервалов варьирования.
Факторы кодируют по формуле
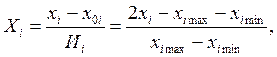 (3)
(3)
где: X i - кодированное без размерное значение фактора;
x i - натуральное размерное значение фактора; i - номер фактора;
 - натуральное значение основного (нулевого) уровня фактора, исходная точка для построения плана эксперимента;
- натуральное значение основного (нулевого) уровня фактора, исходная точка для построения плана эксперимента;
И i =  - интервал варьирования фактора, это некоторое число (свое для каждого фактора) прибавление которого к основному уровню дает верхний, а вычитание - нижний уровень фактора. Интервал не может быть меньше ошибки метода измерений фактора, он также не должен выходить за пределы области определения фактора.
- интервал варьирования фактора, это некоторое число (свое для каждого фактора) прибавление которого к основному уровню дает верхний, а вычитание - нижний уровень фактора. Интервал не может быть меньше ошибки метода измерений фактора, он также не должен выходить за пределы области определения фактора.
Для первого фактора И 1 = (1420 – 1220)/2 = 200; для второго И 2 = (10 – 5,5)/2 = 7,75.
Верхний уровень кодированного фактора обозначают + 1, а нижний - 1, часто для упрощения записи в матрицах планирования единицы не отмечают, а оставляют только знаки (+) или (-).
Проверим формулу (3) по данным табл. 2:
верхний уровень Х 1В =  = + 1; нижний уровень Х 1Н =
= + 1; нижний уровень Х 1Н =  = - 1;
= - 1;
основной уровень Х 1,0 =  = -0.
= -0.
На основе рабочей матрицы табл. 2 составим табл. 3 - матрицу планирования ПФЭ для аварий в средней полосе (столбец 3 табл. 1).
Таблица 3
Матрица планирования ПФЭ типа 22
с расчетным столбцом взаимовлияния факторов
| N опыта
| Кодированные переменные (факторы)
| Выход процесса 
|
|
| Х 0
| Х 1
| Х 2
| Х 1 Х 2
|
|
|
| +
| -
| -
| +
| (37+39)/2 = 38
|
|
| +
| +
| -
| -
| (57+59)/2 = 58
|
|
| +
| -
| +
| -
| (69+71)/2 = 70
|
|
| +
| +
| +
| +
| (104+106) = 105
|
| N = 4
| b 0
| b 1
| b 2
| b 1,2
| n = 2
|
Матрица планирования образуется следующим образом. Для первого фактора знаки чередуются через один (-,+,-,+); для второго – через два (-,-,+,+), для третьего – через четыре и т.д. по степеням двойки. Знаки под взаимовлиянием факторов получены как произведение знаков по горизонтали. Под Х 0 все знаки «плюс».
Знаки указывают на условия проведения опытов.
1-й опыт выполнен при нижних значениях факторов (-, -) 1020 и 5,5; получены два экспериментальных значения: 37 и 39, по ним вычислено среднее арифметическое (37+39)/2 = 38 – верхняя строка табл. 1.
2-й опыт: 1-й фактор на верхнем уровне (+) 1420, 2-й – на нижнем (-) 5,5; получили (57+59)/2 = 58 – 3-я строка снизу.
3-й опыт: 1-й фактор на нижнем (-) уровне 1020, 2-й – на верхнем (+) 10,0; получили (69+71)/2 = 70 – 3-я строка сверху.
4-й опыт: оба фактора на верхнем уровне (+, +) 1420 и 10,0; получили (104+106)/2 = 105 – нижняя строка табл. 1.
Матрица планирования эксперимента должна обладать следующими основными свойствами:
1 - симметричность относительно центра эксперимента - алгебраическая сумма элементов столбца каждого фактора равна нулю;
2 - ортогональность - сумма почленных произведений двух любых столбцов матрицы равна нулю, это очень важное свойство позволяет вычислять коэффициенты регрессии уравнения независимо друг от друга;
3 - ротатабельность - точность предсказания параметра оптимизации (дисперсия) одинакова на равных расстояниях от центра эксперимента и не зависит от направления.
Матрица планирования, приведенная в табл. 3, соответствует предъявленным к ней требованиям. Для любого столбца, кроме Х 0 выполняется условие симметричности относительно центра эксперимента - количество плюсов и минусов одинаково, матрица ортогональна - например, проверим два последних столбца, при перемножении получим следующие знаки (- + - +), сумма этих знаков равна нулю.
Любая случайная величина характеризуется законом распределения вероятностей. Предположим, что значения параметра оптимизации " y " распределены по нормальному закону, в этом случае " y " можно полностью охарактеризовать двумя величинами: математическим ожиданием (средним значением) -  и дисперсией - S 2.
и дисперсией - S 2.
Для оценки ротатабельности матрицы проверим однородность дисперсий параллельных опытов (реализаций) - однородность построчных дисперсий по критерию Кохрена (Кочрена) - G. Рассчитываем построчные дисперсии повторных наблюдений (параллельных опытов, реализаций) по формуле:
 (4)
(4)
где f 1 = n - 1 - число степеней свободы, равное количеству параллельных наблюдений (n) минус единица. Для нашего случая n = 2.
Одна степень свободы использована для вычисления среднего -  .
.
Например, для опыта N 1 будем иметь следующий результат:

Такие же результаты получим для других опытов: ∑ S i2 = 2х4 = 8.
Определяем расчетное значение критерия Кохрена:
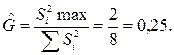 (5)
(5)
По рис. 2 определяем критическое значение критерия для числа степеней свободы: числителя - f 1 = n - 1 и знаменателя f 2 = N = 4 при выбранном уровне значимости P = 0,05 (доверительная вероятность 0,95 или 95%). По оси абсцисс рис. 2 находим f 2 = 4, по вертикали поднимаемся до линии G при f 1 = 1, по горизонтали смещаемся вправо на шкалу и получаем G кр = 0,9. Так как критическое значение критерия больше расчетного G кр = 0,9 > G = 0,25, то дисперсии однородны, то есть точность опытов одинакова.
Определяем дисперсию воспроизводимости эксперимента (параметра оптимизации) и среднеквадратическую ошибку (стандарт) эксперимента:
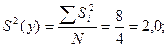
 (6)
(6)
Из условия ортогональности матрицы для ПФЭ дисперсии и ошибки всех коэффициентов регрессии равны между собой и определяются:

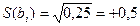 или
или
 (7)
(7)
Определяем доверительный интервал для коэффициентов регрессии:
D b i = ± tкр × S(bi) = 2,8 ×0,5 = ± 1,4, (8)
где t кр - критическое значение критерия Стьюдента определяем при числе степеней свободы f = N (n - 1) = 4 на шкале абсцисс рис. 3. По вертикали достигаем линии характеризующей табличные значения критерия t при заданном уровне значимости P = 0,05, сносим вправо это значение и получаем результат t кр = 2,8.
Доверительный интервал D b используется для оценки статистической значимости коэффициентов регрессии уравнения. Если коэффициент регрессии по абсолютной величине меньше доверительного интервала, то он статистически незначим.
Для вычисления коэффициентов регрессии необходимо просуммировать средние значения параметра оптимизации - y i (предпоследний столбец табл. 3) со знаком соответствующего столбца матрицы и разделить на число опытов - N.
Выход процесса (параметр оптимизации) в центре факторного пространства при основном (нулевом) уровне факторов составит:
b 0 =  = 67,75.
= 67,75.
Влияние на процесс первого фактора - диаметр трубы оценивается коэффициентом регрессии:
b 1 = 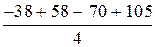 = 13,75.
= 13,75.
Влияние второго фактора - давление газа в магистрали:
b 2 =  = 19,75.
= 19,75.
Взаимовлияние двух факторов:
b 1,2 =  = 3,75.
= 3,75.
Все коэффициенты регрессии статистически значимы, так как абсолютная величина этих коэффициентов больше доверительного интервала - D b = 1,4.
Уравнение регрессии, описывающее влияние диаметра трубы и давления газа в ней на среднее время ликвидации отказа магистрального трубопровода в средней полосе, будет иметь следующий вид:
У = 67,75 + 13,75 Х 1 + 19,75 Х 2 + 3,75 Х 1 Х 2. (9)
Проверим полученное уравнение для условий опыта 4:
У 4 = 67,75 + 13,75 + 19,75 + 3,75 = 105.
Последний этап планирования и реализации ПФЭ заключается в проверке адекватности модели - способности прогнозировать результаты опытов и хорошо описывать поверхность отклика. Для проверки адекватности вычисляют оценку дисперсии адекватности по формуле:
 (10)
(10)
где: f ад = N - В - число степеней свободы;
N - число опытов ПФЭ;
B - число значимых коэффициентов регрессии;
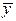 - среднее значение параметра оптимизации параллельных реализаций;
- среднее значение параметра оптимизации параллельных реализаций;
 - расчетное значение параметра оптимизации.
- расчетное значение параметра оптимизации.
Числом степеней свободы называется разность между числом опытов и числом статистически значимых коэффициентов, определяемых независимо друг от друга. Возможны три случая:
1. Число степеней свободы положительно - f > 0. Это соответствует ненасыщенным планам. В такой ситуации, кроме оценки всех неизвестных констант, возможна также проверка адекватности уравнения;
2. Если число степеней свободы равно нулю, то возникают насыщенные планы. В этом случае можно оценить все константы, но не хватает "свободы" для проверки модели.
3. При f < 0 - планы сверхнасыщенные, здесь возможна оценка только некоторых из неизвестных величин.
В нашем случае дисперсию адекватности рассчитать невозможно, так как все коэффициенты регрессии статистически значимы, число степеней свободы равно нулю, а расчетные значения параметра оптимизации совпадают со средними значениями. В таких случаях необходимо выполнить дополнительные опыты в центральной зоне факторного пространства и сопоставить экспериментальные данные с расчетными.
Адекватность уравнения проверим в центральной зоне факторного пространства при Д = 1220 мм, Р = 7,5 МПа и параметре оптимизации У = 65 – средняя строка табл. 1.
Закодируем натуральные значения факторов по формуле (3):
 Х 1 =
Х 1 =  = 0; Х 2 =
= 0; Х 2 =  = - 0,11.
= - 0,11.
Подставляем полученные значения в уравнение регрессии (9)
У = 67,75 + 13,75 Х 1 + 19,75 Х 2 + 3,75 Х 1 Х 2. (9)
Расчетное значение параметра оптимизации при этих условиях:
У = 67,75 + 19,75 (- 0,11) = 65,58.
Относительная погрешность расчетного значения по сравнению с экспериментальным невелика (∆ У = 100 (65,58 – 65,0) / 65 = 0,89%), что позволяет сделать вывод об адекватности полученного уравнения ПФЭ. Где У = 65 – значение параметра оптимизации.
Коэффициенты уравнения регрессии для аварийных остановок в средней полосе:
b 0 =  = 42; b 1 =
= 42; b 1 = 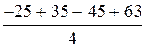 = 7;
= 7;
b 2 =  = 12; b 1,2 =
= 12; b 1,2 =  = 2.
= 2.
Получили уравнение
У = 42 + 7 Х 1 + 12 Х 2 + 2 Х 1 Х 2.
Коэффициенты уравнения регрессии для условий Севера в два раза больше коэффициентов средней полосы (табл. 1).
b 0 =  = 135,5 и т.д.
= 135,5 и т.д.
Адекватность уравнения обычно оценивают с помощью критерия Фишера.
Если расчетное значение критерия Фишера меньше критического,  , то полученное уравнение регрессии адекватно описывает результаты эксперимента.
, то полученное уравнение регрессии адекватно описывает результаты эксперимента.
Если модель неадекватна, то возможны следующие решения:
· достройка плана эксперимента до более полного, например, до модели второго порядка;
· разбивка области эксперимента на несколько подобластей за счет уменьшений интервалов варьирования, описание каждой отдельно;
· перенесение центра плана эксперимента;
· преобразование зависимых и независимых переменных.
Дополнительные опыты в центральной зоне факторного пространства (как правило, Х i = 0) целесообразно выполнять в любом случае, даже при положительной оценке с помощью критерия Фишера. В приведенном ранее примере Х 1 ¹ 0 по ограничениям испытательного стенда. Иногда опыты в матрице планирования не дублируют (n = 1), в таком случае дисперсию воспроизводимости эксперимента оценивают по нескольким опытам, выполненным при нулевом уровне факторов (n 0» 5).
Интерпретация результатов
Интерпретация модели - это перевод модели с абстрактного математического языка на язык экспериментатора. Он включает оценку величины и направления влияния отдельных факторов и их взаимодействий, сопоставление влияния совокупности факторов, проверку правильности априорных представлений и в некоторых случаях проверку и выдвижение гипотез о механизме процесса.
На первом этапе интерпретации устанавливается, в какой мере каждый фактор влияет на параметр оптимизации. Величина коэффициента регрессии - количественная мера этого влияния. Чем больше коэффициент, тем сильнее влияет фактор.
О характере влияния факторов говорят знаки коэффициентов. Если коэффициент имеет знак "плюс", то с увеличением значения фактора параметр оптимизации увеличивается, а знак "минус" - уменьшается.
Величина коэффициента соответствует вкладу данного фактора на величину параметра оптимизации при переходе с основного уровня на верхний или нижний. Основной или главный эффект равен удвоенному коэффициенту.
Анализ уравнения (9) показывает, что наибольшее влияние на параметр оптимизации оказывает второй фактор Х 2 – b 2 = 19,75; следующий по значимости первый фактор Х 1 – b 1 = 13,75; Главный эффект для первого фактора составит 2 × 13,75 = 27,5.
b 0 = 67,75 - это значение параметра оптимизации в центре плана на нулевом уровне факторов.
Коэффициенты при произведениях факторов оценивают эффект их взаимодействия - величину нелинейности модели, связанную с тем, что эффект одного фактора зависит от уровня, на котором находится другой фактор.
Если эффект взаимодействия имеет положительный знак, а линейные эффекты имеют одинаковый знак, то для увеличения параметра оптимизации требуется одновременное увеличение или уменьшение значений факторов. Для уменьшения параметра оптимизации факторы должны одновременно изменяться в разных направлениях.
Если эффект взаимодействия имеет отрицательный знак, а линейные эффекты - положительный, то для увеличения " y " факторы должны изменяться в разных направлениях.
Если эффект взаимодействия имеет положительный знак, а соответствующие линейные эффекты - отрицательные, то выбор однозначен: -1 и -1.
В уравнении (9) взаимодействие факторов Х 1 и Х 2 - b 1,2 = 3,75. Для уменьшения параметра " y " надо снижать значение этих факторов.
Изменение интервалов варьирования приводит к изменению коэффициентов регрессии.
Из кодированных переменных уравнение можно перевести в натуральные переменные, используя формулы (3) кодирования факторов. Коэффициенты регрессии изменяются, при этом пропадает возможность интерпретации влияния факторов по величине и знакам коэффициентов регрессии. Теряется свойство ортогональности, коэффициенты регрессии будут зависеть друг от друга.
Такой переход целесообразен, если поставлена задача получения интерполяционной формулы в натуральных переменных. Возможны различные ситуации по адекватности и неадекватности модели, значимости и не значимости коэффициентов регрессии, положению оптимума.
Для линейной адекватной модели со значимыми коэффициентами регрессии возможны: движение по градиенту, план второго порядка, окончание исследования.
Если часть коэффициентов регрессии статистически незначима, то возможны следующие варианты: изменение интервалов варьирования, перенос центра плана, отсеивание незначимых факторов, параллельные опыты, достройка плана; а также движение по градиенту, а если область оптимума близка, то реализация плана второго порядка или окончание исследования.
Если все коэффициенты незначимы, то реализуется план второго порядка или исследование заканчивается, также возможны предыдущие варианты.
Для неадекватной линейной модели, если область оптимума близка, то исследование или заканчивается, или реализуется план второго порядка. Такие решения, как изменение интервалов варьирования, перенос центра плана, достройка плана или движение по градиенту применяются при любом положении оптимума.
Возможно включение в модель эффектов взаимодействия факторов и движение с помощью неполного полинома второго порядка, а также оценка квадратичных эффектов для получения информации о кривизне поверхности отклика перед движением по градиенту.
Если поставлена задача построения интерполяционной формулы, то исследование заканчивается на получении адекватной модели, в случае неадекватной модели возможны: включение в модель эффектов взаимодействия, достройка плана, преобразование переменных, изменение интервалов варьирования.
Поверхность отклика
Одним из методов, значительно облегчающим классификацию и интерпретацию сложных моделей, является их геометрическое представление. Для этого все направления изменения факторов трактуются как ортогональные оси многомерного пространства факторов. При двухфакторной зависимости У = j (Х1, Х2) пространство факторов представляет собой плоскость с осями Х 1 и Х 2, а любое сочетание факторов характеризуется точкой на этой плоскости с координатами x1, x2. При трехфакторной зависимости данное сочетание факторов характеризуется точкой в трехмерном пространстве с координатами x1, x2, x3. Так как пространство модели " y " кроме осей " x " содержит также и ось " y ", то размерность пространства модели равна " k + 1", то есть всегда на единицу больше размерности пространства факторов.
Графически (в аксонометрии) невозможно изобразить более чем трехмерное пространство.
Функция y = j (x1, x2) геометрически интерпретируется как некоторая поверхность в трехмерном пространстве (плоскость, часть сферы и т.д.). Для наименования аналогичной поверхности в К - мерном пространстве (где k > 3) используется, как правило, тот же термин, но с приставкой "гипер".
Так, например, геометрическое представление функции y = b 0 + b 1x1 - это прямая на плоскости x1y; функции y = b 0 + b 1x1 + b 2x2 - это плоскость в трехмерном пространстве x1, x2, y. Функция y = b 0 + b 1x1 + b 2x2 + b 3 x3 - это гиперплоскость в четырехмерном пространстве и т.д.
При описании поверхности широко применяется аддитивная (суммирующая) модель. Это объясняется тем, что как бы ни была сложна поверхность отклика многофакторного эксперимента, её малые участки, не содержащие экстремальных точек, с достаточным приближением могут быть заменены участками плоскости, касательными к кривой поверхности в центре этого участка. Это так называемое " чешуйчатое", или " граненое ", описание кривой поверхности, которое позволяет получить ценные сведения о такой поверхности.
В частности, по этой модели можно узнать "высоты" участков поверхности, углы и направления склонов, определить положение и направление изолиний и т.п., то есть иногда такое " граненое " описание кривой поверхности часто оказывается очень удобным. Основным недостатком аддитивной модели является то, что для каждой соседней грани все коэффициенты модели должны определяться заново, так как. при переходе от грани к грани они получают новые значения.
Протяженность каждой грани аддитивной модели могла бы быть существенно увеличена, если бы эти грани были не плоскими, а искривленными. Этого можно достигнуть, переходя от аддитивных моделей первого порядка (включающих Хi только в первой степени) к аддитивным же моделям второго, третьего и более высоких порядков (включающих Хi2, Хi3 и т.д.). Но такие модели очень сложны.
Есть еще один вид поверхности, который занимает промежуточное положение - это винтовая поверхность, сечения которой как вдоль оси x1, так и x2 являются прямыми линиями, но наклон их линейно изменяется с изменением координаты. Это частный случай многомерного гиперболоида.
Модель поверхности в виде многомерного гиперболоида часто позволяет существенно уменьшить погрешность адекватности при описании изогнутых поверхностей отклика. Поэтому в современной теории планирования эксперимента эта модель, по существу, заняла доминирующее положение. Модель учитывает эффекты взаимодействия факторов: парные, тройные и т.д. Однако при увеличении числа факторов " k " модель в виде гиперболоида становится чрезвычайно громоздкой.
Поверхность отклика ПФЭ типа 22 приведены на рис. 1. В нижней части рисунка изображено факторное пространство, по которому проведены оси факторов с обозначением их уровней (+1, 0, -1), по углам факторного пространства обозначены условия проведения опытов.
Например, опыт N4 слева внизу выполнен при верхних уровнях обоих факторов (+, +), а опыт N1 справа вверху - при нижних уровнях (-, -) и т.д. Над факторным пространством построена поверхность отклика двухфакторной модели ПФЭ типа 22 по уравнению (9).
Подставляя значения уровней факторов (+1, -1) в уравнение (9), соответствующие условиям проведения опытов, получим расчетные значения параметра оптимизации:
 '1 = 67,75 - 13,75 - 19,75 + 3,75 = 38
'1 = 67,75 - 13,75 - 19,75 + 3,75 = 38
 '2 = 67,75 + 13,75 - 19,75 - 3,75 = 58
'2 = 67,75 + 13,75 - 19,75 - 3,75 = 58
 '3 = 67,75 - 13,75 + 19,75 - 3,75 = 70
'3 = 67,75 - 13,75 + 19,75 - 3,75 = 70
 '4 = 67,75 + 13,75 + 19,75 + 3,75 = 105
'4 = 67,75 + 13,75 + 19,75 + 3,75 = 105
Аналогично рассчитываются результаты для других условий.
Откладываем ординаты, соответствующие результатам расчетов, над точками условий выполнения опытов. Соединяем эти точки (38; 58; 70; 105) прямыми линиями - получили периметр поверхности отклика, Для наглядности нанесем на поверхность штриховые линии - получили геометрическое отображение модели (9). Поверхность отклика ПФЭ типа 22 - это плоскость, образованная параллельными линиями.
Средние линии проведены по плоскости между точками 5' и 6' для фактора Х1 , а также между точками 7' и 8' для фактора Х2.
Поверхность отклика дает наглядное представление о модели.
Средние линии плоскости пересекаются над нулевой точкой факторного пространства, ордината над этой точкой равна y 0 = b 0 =67,75.
Коэффициенты полинома модели являются частными производными функции отклика по соответствующим переменным. Их геометрический смысл - тангенсы углов наклона плоскости к соответствующей оси. Из точки нулевого уровня плоскости b 0 = 67,75 проведем оси x 1' и x 2' параллельные осям факторов x 1 и x 2. Через эту же точку над осями факторов проведем средние линии плоскости. Вдоль оси x 1 средняя линия соединяет точки 5' и 6' : У 5' = (58 + 105)/2 = 81,5 и У 6' = (38 +70)/2 = 54; вдоль оси x 2 - точки 7' и 8' : У 7' = (70 + 105)/2 = 87,5 и У 8' = (38 +58)/2 = 48.
Углы a1 и a2 между этими средними линиями и осями x 1', x 2' характеризуют влияние факторов. Так как прилежащие катеты равны единице, то коэффициенты регрессии можно определить непосредственно из рисунка, измерив второй - противолежащий катет или вычислив разность между значением параметра оптимизации над точками: + 1 и b 0.
Например, b 1 = 81,5 - 67,75 = 13,75; b 2 = 87,5 - 67,75 = 19,75.
По рисунку можно определить и парные эффекты взаимовлияния факторов. Это расстояние на линии от нулевой точки факторов к поверхности отклика, соединяющее точку пересечения средних линий " b0 " и диагоналями. Оно также равно половине расстояния между диагоналями на этой линии. На рисунке - b 1,2 = 3,75.
 Полученное в результате исследований уравнение регрессии и построенная поверхность отклика позволяют рассчитать результаты как внутри факторного пространства, так и за его пределами.
Полученное в результате исследований уравнение регрессии и построенная поверхность отклика позволяют рассчитать результаты как внутри факторного пространства, так и за его пределами.
Интерполяция позволяет определить значения параметра оптимизации внутри факторного пространства. Например, надо определить параметр оптимизации при следующих условиях: Х 1 = + 0,5 и Х2 = - 0,5.
 9 =
9 =  (0,5; - 0,5) = 67,75 + (13,75 × 0,5) + (19,75 × - 0,5) + (3,75× 0,5 × - 0,5) = 63,81.
(0,5; - 0,5) = 67,75 + (13,75 × 0,5) + (19,75 × - 0,5) + (3,75× 0,5 × - 0,5) = 63,81.
Экстраполяция - это определение параметра оптимизации за пределами исследованного факторного пространства. Например, если Х1 = 1,2; Х2 = 0,5; то:
 (1,2; 0,5) = 67,75 + 13,75 × 1,2 + 19,75 × 0,5 + 3,75 × 1,2 × 0,5 = 96,4
(1,2; 0,5) = 67,75 + 13,75 × 1,2 + 19,75 × 0,5 + 3,75 × 1,2 × 0,5 = 96,4
Точность определения параметра оптимизации при экстраполяции ниже, чем при интерполяции, так как согласно свойству матрицы планирования - ротатабельности, дисперсия растет при увеличении радиуса исследуемого пространства - расстояния от нулевой точки.
y = 42 + 7 Х1 + 12 Х 2 + 2 Х1Х2.

Рис. 1. Поверхность отклика ПФЭ типа 22

Рис. 2. Значения критериев Фишера (F) и Кохрена (G) в зависимости
от числа степеней свободы

Рис. 3. Значения критериев Пирсона (l 2) и Стьюдента (t) в зависимости
от числа степеней свободы
2. ПРАКТИЧЕСКАЯ РАБОТА «ПФЭ ТИПА 22»
Исходные данные
1) y ̅: 35;56;68;103 18) y ̅: 33;54;66;101 35) y ̅: 34;56;68;105
2) y ̅: 36;56;68;103 19) y ̅: 35;55;68;103 36) y ̅: 35;56;69;103
3) y ̅: 35;56;67;103 20) y ̅: 37;56;68;102 37) y ̅: 35;56;68;103
4) y ̅: 35;57;68;103 21) y ̅: 35;56;66;103 38) y ̅: 38;56;68;101
5) y ̅: 39;56;68;100 22) y ̅: 35;58;68;103 39) y ̅: 35;56;65;103
6) y ̅: 35;56;68;103 23) y ̅: 40;56;68;99 40) y ̅: 35;59;68;103
7) y ̅: 35;60;68;103 24) y ̅: 35;56;69;103 41) y ̅: 41;56;68;103
8) y ̅: 42;56;68;104 25) y ̅: 35;61;68;103 42) y ̅: 35;56;70;103
9) y ̅: 35;56;71;103 26) y ̅: 43;56;68;105 43) y ̅: 35;56;68;103
10) y ̅: 35;56;68;103 27) y ̅: 35;56;72;103 44) y ̅: 44;62;68;106
11) y ̅: 45;63;68;107 28) y ̅: 35;56;68;108 45) y ̅: 35;56;73;109
12) y ̅: 35;56;74;103 29) y ̅: 33;64;68;103 46) y ̅: 35;56;68;103
13) y ̅: 35;56;68;103 30) y ̅: 35;56;75;102 47) y ̅: 32;65;68;103
14) y ̅: 31;66;68;103 31) y ̅: 35;56;68;103 48) y ̅: 35;56;76;101
15) y ̅: 35;56;68;100 32) y ̅: 30;55;68;103 49) y ̅: 35;56;68;103
16) y ̅: 35;56;68;103 33) y ̅: 35;56;67;102 50) y ̅: 36;54;68;103
17) y ̅: 37;53;68;103 34) y ̅: 35;56;68;103 51) y ̅: 35;56;66;103
Порядок выполнения работы
1. Повторить теоретический материал по теме практической работы.
2. Выбрать исходные данные в соответствии с номером студента в журнале группы. В исходных данных приведены средние арифметические значения при n =2. Например, для первого варианта опыт №1, при нижних уровнях факторов, y 1 = (34 + 36)/2 = 35 и т.д.
3. Заполнить таблицы. В табл. 1 заполняем три столбца - данные только аварий в средней полосе, заменяя выделенные жирным шрифтом цифры на свои исходные данные. Например, для первого варианта y 1 = (34+36)/2 = 35 вместо 38; опыт №2, выполненный при верхнем уровне первого фактора и нижнем уровне второго фактора (см. табл. 3), y 2 = (55+57)/2 = 56 вместо 58 (см. табл. 1 третья строка снизу) и т.д.
4. Рассчитываем дисперсии параллельных опытов по формуле 3.
5. Определяем расчетное значение критерия Кохрена по формуле 5.
6. По рис. 2 определяем критическое значение критерия Кохрена, сопоставляем его с расчетным значением и оцениваем однородность построчных дисперсий.
7. Определяем дисперсию воспроизводимости эксперимента и среднеквадратическую ошибку (стандарт) эксперимента по формулам 6.
8. Рассчитываем дисперсии и ошибки всех коэффициентов регрессии по формулам 7.
9. Определяем доверительный интервал для коэффициентов регрессии по формуле 8.
10. Вычитываем коэффициенты регрессии, оцениваем их статистическую значимость и записываем уравнение регрессии, аналогичное уравнению 9.
11. Проверяем полученное уравнение регрессии для условий одного из опытов.
12. Проверяем адекватность полученного уравнения в центральной зоне факторного пространства при условиях, заданных в средней строке табл. 1.
13. Выполним интерпретацию уравнения в соответствии с подразделом 1.2..
14. Аккуратно строим поверхность отклика в соответствии с подразделом 1.3, обозначаем на ней коэффициенты уравнения, выполняем интерполяцию и экстраполяцию.
ТЕСТЫ
Требования к объекту исследования?
1. Динамичность и состоятельность.
2. Управляемость и однозначность.
3. Состоятельность, несмещенность и эффективность.
4. Воспроизводимость результатов и управляемость.
2. Область определения фактора?
1. Совокупность ограниченного числа значений данного фактора в матрице планирования эксперимента.
2. Совокупность всех значений, которые в принципе может принимать данный фактор.
3. Совокупность всех значений данного фактора в матрице планирования эксперимента.
4. Совокупность ограниченного числа значений, которые в принципе может принимать данный фактор.
Интерпретация модели?
1. Это перевод модели с абстрактного языка на язык экспериментатора.
2. Это статистическое оценивание коэффициентов модели.
3. Это графическое представление математической модели.
4. Это использование статистических критериев при оценке адекватности модели.



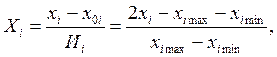 (3)
(3) - натуральное значение основного (нулевого) уровня фактора, исходная точка для построения плана эксперимента;
- натуральное значение основного (нулевого) уровня фактора, исходная точка для построения плана эксперимента; - интервал варьирования фактора, это некоторое число (свое для каждого фактора) прибавление которого к основному уровню дает верхний, а вычитание - нижний уровень фактора. Интервал не может быть меньше ошибки метода измерений фактора, он также не должен выходить за пределы области определения фактора.
- интервал варьирования фактора, это некоторое число (свое для каждого фактора) прибавление которого к основному уровню дает верхний, а вычитание - нижний уровень фактора. Интервал не может быть меньше ошибки метода измерений фактора, он также не должен выходить за пределы области определения фактора. = + 1; нижний уровень Х 1Н =
= + 1; нижний уровень Х 1Н =  = - 1;
= - 1; = -0.
= -0.
 и дисперсией - S 2.
и дисперсией - S 2. (4)
(4)
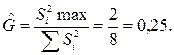 (5)
(5)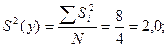
 (6)
(6)
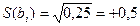 или
или (7)
(7) = 67,75.
= 67,75.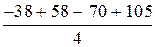 = 13,75.
= 13,75. = 19,75.
= 19,75. = 3,75.
= 3,75. (10)
(10)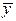 - среднее значение параметра оптимизации параллельных реализаций;
- среднее значение параметра оптимизации параллельных реализаций; - расчетное значение параметра оптимизации.
- расчетное значение параметра оптимизации. Х 1 =
Х 1 =  = 0; Х 2 =
= 0; Х 2 =  = - 0,11.
= - 0,11. = 42; b 1 =
= 42; b 1 = 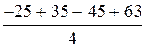 = 7;
= 7; = 12; b 1,2 =
= 12; b 1,2 =  = 2.
= 2. = 135,5 и т.д.
= 135,5 и т.д. , то полученное уравнение регрессии адекватно описывает результаты эксперимента.
, то полученное уравнение регрессии адекватно описывает результаты эксперимента. '1 = 67,75 - 13,75 - 19,75 + 3,75 = 38
'1 = 67,75 - 13,75 - 19,75 + 3,75 = 38 Полученное в результате исследований уравнение регрессии и построенная поверхность отклика позволяют рассчитать результаты как внутри факторного пространства, так и за его пределами.
Полученное в результате исследований уравнение регрессии и построенная поверхность отклика позволяют рассчитать результаты как внутри факторного пространства, так и за его пределами. 9 =
9 =  (0,5; - 0,5) = 67,75 + (13,75 × 0,5) + (19,75 × - 0,5) + (3,75× 0,5 × - 0,5) = 63,81.
(0,5; - 0,5) = 67,75 + (13,75 × 0,5) + (19,75 × - 0,5) + (3,75× 0,5 × - 0,5) = 63,81. (1,2; 0,5) = 67,75 + 13,75 × 1,2 + 19,75 × 0,5 + 3,75 × 1,2 × 0,5 = 96,4
(1,2; 0,5) = 67,75 + 13,75 × 1,2 + 19,75 × 0,5 + 3,75 × 1,2 × 0,5 = 96,4





