Эмпирическая функция. Статистическим аналогом функции распределения  , или эмпирической функцией распределения выборки, является ступенчатая функция со скачками высотой
, или эмпирической функцией распределения выборки, является ступенчатая функция со скачками высотой  в каждой точке xi:
в каждой точке xi:
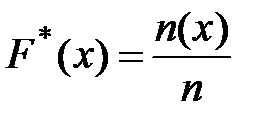 ,
,
где n(x) – число наблюдений, величина которых не превосходит x. Таким образом, является функцией от выборочных значений и равной частоте события n(x)<x при n повторных экспериментах.
Зам. Если имеется статистический ряд распределения (см. таблицу 1), то  является ступенчатой функцией со скачками высотой
является ступенчатой функцией со скачками высотой 
Построение эмпирической функции распределения позволяет детально сравнить теорию с выборочными результатами.
Гистограмма. При больших значениях n строить  затруднительно, поэтому выборки часто подвергаются группировке. При этом отдельные выборочные значения не даются, а указываются лишь число выборочных значений попавших в интервалы некоторого определённого разбиения.
затруднительно, поэтому выборки часто подвергаются группировке. При этом отдельные выборочные значения не даются, а указываются лишь число выборочных значений попавших в интервалы некоторого определённого разбиения.
Статистическим аналогом плотности распределения является величина:
 (1)
(1)
Её график получил название гистограммы. Величина  пропорциональна относительной частоте попадания случайной величины в j – й интервал, поэтому она является случайной величиной.
пропорциональна относительной частоте попадания случайной величины в j – й интервал, поэтому она является случайной величиной.
При построении гистограммы разбивают область значений на интервалы (классы) и для каждого интервала определяют частоту попадания в него выборочных значений. Гистограмму строят как ступенчатую функцию, которая на каждом интервале принимает постоянное значение, которое определяется по формуле (1). По виду гистограмма представляет собой фигуру из  смежных столбиков, с основаниями на интервалах (классах) группировки. Причём высота каждого столбика, пропорциональна частоте наблюдений в его интервале и обратно пропорциональна длине интервала и объёму выборки n (при этом площадь столбика получается равной относительной частоте, а площадь гистограммы равной единице).
смежных столбиков, с основаниями на интервалах (классах) группировки. Причём высота каждого столбика, пропорциональна частоте наблюдений в его интервале и обратно пропорциональна длине интервала и объёму выборки n (при этом площадь столбика получается равной относительной частоте, а площадь гистограммы равной единице).
При разбиении на интервалы рекомендуется принимать длину интервала постоянной: h =(xmax-xmin)/ k, а число интервалов k выбирать в зависимости от числа наблюдений. Значениям выборки xi, попавшим в один и тот же интервал j, присваивается значение середины данного интервала  .
.
При выборе ширины интервала для фиксированного n необходимо по возможности учитывать следующие положения:
1. Ширина интервала h – постоянная;
2. Число интервалов k обычно колеблется от 5 до 15.
В зависимости от величины n можно использовать следующие рекомендации [1]:
k ≈  ; k≈5lg n; k≈1+3.2lg n [1] или таблицей 6 [2].
; k≈5lg n; k≈1+3.2lg n [1] или таблицей 6 [2].
таблица 6
| Число наблюдений
| Рекомендуемое число наблюдений
|
| 40 – 100
| 7…9
|
| 100 – 500
| 8…12
|
| 500 – 1000
| 10…16
|
| 1000 – 10000
| 12…22
|
На практике количество интервалов и их размеры подбираются также с учётом, чтобы в каждом было не менее пяти наблюдений (за исключением, возможно, крайних интервалов). Минимальное число интервалов должно быть равным пяти, т.е. k ≥5. Это связано с тем, что согласно центральной предельной теореме сумма случайных величин имеет приближённо нормальное распределение (на практике число случайных величин достаточно взять не менее пяти).
По одной выборке можно построить множество гистограмм, варьируя n, k, h, поэтому за исключением случаев, когда n велико, гистограмма может употребляться лишь для грубого сравнения, в то время как эмпирическая функция распределения может быть использована для всякого детального сравнения с теоретическим распределением.
Зам. В статистических пакетах при построении гистограммы высоту столбиков, как правило, выбирают равной частоте попадания ni (см. рис.7).
Составляется таблица группированных данных (см. таблицу 7):
Таблица 7
| № интервала
|
|
| …
| k
|
| Граница
интервалов
| 
| 
|
| 
|
| Частота nj
| n1
| n2
|
| nk
|
| Частность,
относительная частота nj/n
|
n1/n
|
n2/n
|
|
nk/n
|
Для наглядности, сгруппированные статистические ряды представляются графиком и диаграммой. Наиболее распространёнными графиками являются полигон и гистограмма.
Для построения гистограммы выборки на оси абсцисс откладываются частичные интервалы 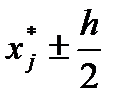 , на каждом из которых строится прямоугольник с высотой
, на каждом из которых строится прямоугольник с высотой  .
.
Если на гистограмме частностей соединить середины интервалов, то полученная замкнутая ломанная образует полигон распределения частностей.
Пример. Для анализа содержания меди в новом месторождении было отобрано 80 проб. Результаты анализов (в граммах) занесены в таблицу 8:
Таблица 8
| 40,26
| 40,35
| 40,44
| 40,35
| 40,39
| 40,40
| 40,42
| 40,32
|
| 40,37
| 40,35
| 40,44
| 40,35
| 40,40
| 40,34
| 40,31
| 40,32
|
| 40,33
| 40,41
| 40,35
| 40,30
| 40,33
| 40,38
| 40,33
| 40,33
|
| 40,28
| 40,30
| 40,40
| 40,36
| 40,32
| 40,32
| 40,42
| 40,35
|
| 40,29
| 40,33
| 40,31
| 40,33
| 40,36
| 40,34
| 40,30
| 40,30
|
| 40,41
| 40,40
| 40,33
| 40,37
| 40,34
| 40,30
| 40,43
| 40,34
|
| 40,35
| 40,34
| 40,34
| 40,31
| 40,43
| 40,36
| 40,34
| 40,34
|
| 40,28
| 40,44
| 40,32
| 40,34
| 40,31
| 40,31
| 40,36
| 40,34
|
| 40,29
| 40,39
| 40,39
| 40,37
| 40,37
| 40,38
| 40,36
| 40,41
|
| 40,27
| 40,38
| 40,37
| 40,37
| 40,36
| 40,35
| 40,32
| 40,36
|
1.Определяем длину частичного интервала  . Число интервалов k=5.
. Число интервалов k=5.
2. За начало первого интервала примем величину, равную 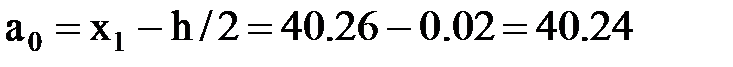 .
.
Группировка исходных данных сведена в таблицу, в каждый интервал включались те значения, числовые значения которых больше нижней границы интервала.
В результате получим таблицу 9.
Таблица 9
| Интервалы
| Границы интервалов
| Середины
интервалов,

| Частота,
ni
| Относительная частота,
ni/n
| Накопленная
относительная частота
|
| Левая
| Правая
|
|
| 40,24
| 40,28
| 40,26
|
| 0,05
| 0,05
|
|
| 40,28
| 40,32
| 40,30
|
| 0,24
| 0,29
|
|
| 40,32
| 40,36
| 40,34
|
| 0,40
| 0,69
|
|
| 40,36
| 40,40
| 40,38
|
| 0,19
| 0,88
|
|
| 40,40
| 40,44
| 40,42
|
| 0,12
| 1,00
|
Контроль:  ;
; 
3. Строим гистограмму и полигон относительных частот.

Рис.4. Гистограмма и полигон выборки
4. Для построения эмпирической функции распределения, воспользуемся данными предыдущей таблицы (см. табл. 9).
Или

Построим график F*(x)

Рис. 5. График эмпирической функции распределения
5. Вычисляем основные числовые характеристики по таблице сгруппированных данных.

 ;
;
 ;
;
 ;
;
 .
.
Для данного примера коэффициент асимметрии положителен, следовательно, график функции плотности распределения имеет правую ветвь более пологую, чем левая (см. рис. 2), а вершина более пологая, чем у нормального закона с данными параметрами (средним и дисперсией), так как коэффициент эксцесса отрицательный.
Замечание 1. Все предыдущие вычисления показывают, что для подсчета числовых характеристик выборки, построения гистограмм требуется большой объём вычислений, поэтому для статистического анализа широко используются различные статистические пакеты [4].
Замечание 2. Еще раз отметим, что гистограмма (полигон) являются статистическими аналогами плотности распределения случай величины, так же и эмпирическая функция распределения, построенная на основе гистограммы или полигона. В численном интегрировании функции одной переменной используют метод прямоугольников (кусочно-линейная аппроксимация подынтегральной функции), что аналогично построению гистограммы и метод трапеций (кусочно-линейная аппроксимация), что аналогично полигона выборки.



 , или эмпирической функцией распределения выборки, является ступенчатая функция со скачками высотой
, или эмпирической функцией распределения выборки, является ступенчатая функция со скачками высотой  в каждой точке xi:
в каждой точке xi: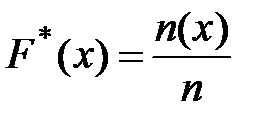 ,
, является ступенчатой функцией со скачками высотой
является ступенчатой функцией со скачками высотой 
 (1)
(1) пропорциональна относительной частоте попадания случайной величины в j – й интервал, поэтому она является случайной величиной.
пропорциональна относительной частоте попадания случайной величины в j – й интервал, поэтому она является случайной величиной. смежных столбиков, с основаниями на интервалах (классах) группировки. Причём высота каждого столбика, пропорциональна частоте наблюдений в его интервале и обратно пропорциональна длине интервала и объёму выборки n (при этом площадь столбика получается равной относительной частоте, а площадь гистограммы равной единице).
смежных столбиков, с основаниями на интервалах (классах) группировки. Причём высота каждого столбика, пропорциональна частоте наблюдений в его интервале и обратно пропорциональна длине интервала и объёму выборки n (при этом площадь столбика получается равной относительной частоте, а площадь гистограммы равной единице). .
. ; k≈5lg n; k≈1+3.2lg n [1] или таблицей 6 [2].
; k≈5lg n; k≈1+3.2lg n [1] или таблицей 6 [2].


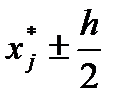 , на каждом из которых строится прямоугольник с высотой
, на каждом из которых строится прямоугольник с высотой  .
. . Число интервалов k=5.
. Число интервалов k=5.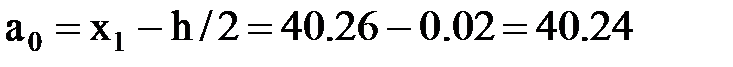 .
.
 ;
; 


 ;
; ;
; ;
; .
.


