

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...
Топ:
Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров...
Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает...
Интересное:
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Цель работы. Изучение возможностей электронных таблиц MS Excel для решения нелинейных уравнений и систем, приобретение навыков работы с компонентом Поиск решения в электронных таблицах.
Задание. Найти корни полинома (табл. 9), решить уравнение (табл. 10) и систему уравнений (табл. 11).
Таблица 12. Варианты заданий
| № | уравнение | № | уравнение |
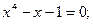 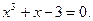
| 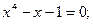 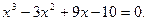
| ||
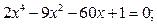 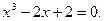
| 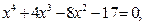 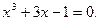
| ||
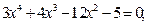 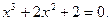
| 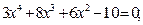 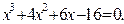
| ||
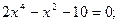 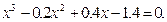
| 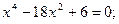 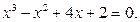
| ||
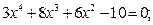 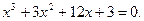
| 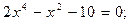 
| ||
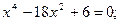 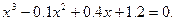
| 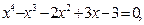 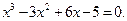
| ||
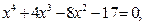 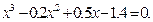
| 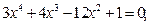 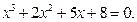
| ||
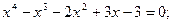 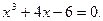
| 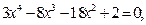 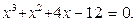
| ||
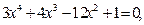 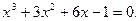
| 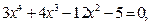 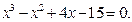
| ||
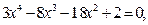 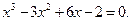
| 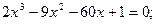 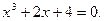
| ||
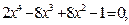 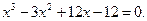
| 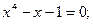 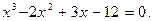
| ||
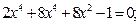 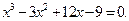
| 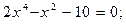 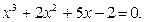
| ||
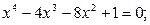 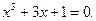
| 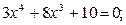 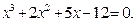
| ||
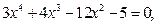 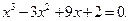
| 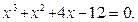 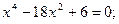
| ||
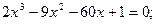 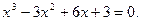
| 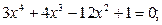 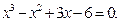
|
Таблица 13. Варианты заданий
| № | уравнение | № | уравнение |
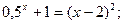 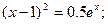
| 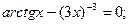 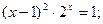
| ||
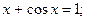 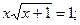
| 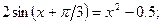 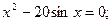
| ||
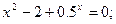 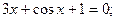
| 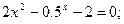 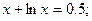
| ||
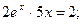 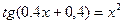
|  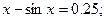
| ||
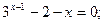 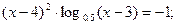
| 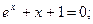 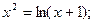
| ||
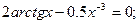 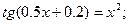
|  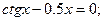
| ||
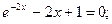 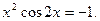
| 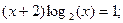 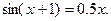
| ||
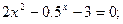 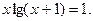
| 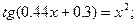 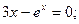
| ||
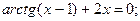 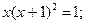
| 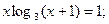 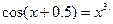
| ||
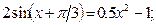 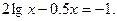
| 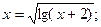 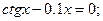
| ||
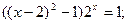 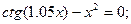
| 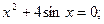 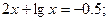
| ||
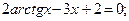 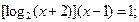
| 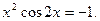 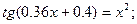
| ||
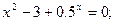 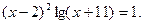
| 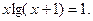 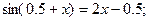
| ||
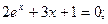 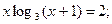
| 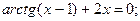 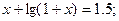
| ||
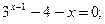 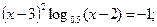
| 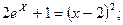 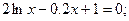
|
Таблица 14. Варианты заданий
| № | Система уравнений | № | Система уравнений |
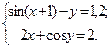 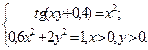
| 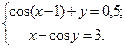 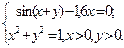
| ||
 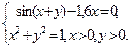
| 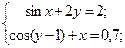 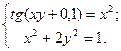
| ||
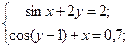 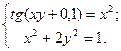
| 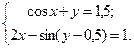 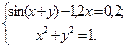
| ||
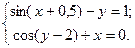 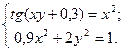
| 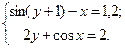 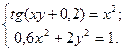
| ||
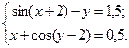 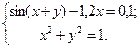
| 20- | 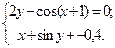 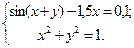
| |
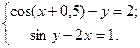 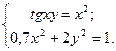
| 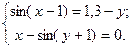 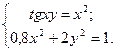
| ||
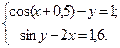 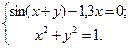
| 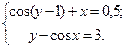 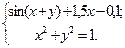
| ||
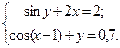 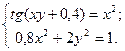
| 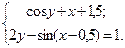 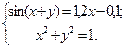
| ||
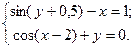 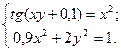
| 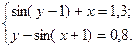 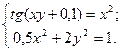
| ||
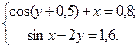 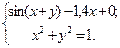
| 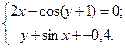 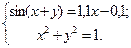
| ||
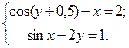 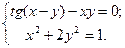
| 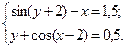 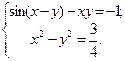
| ||
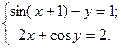 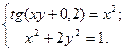
| 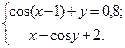 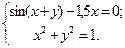
| ||
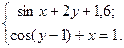 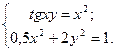
| 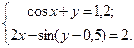 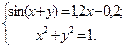
| ||
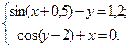 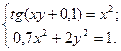
| 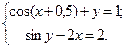 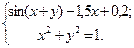
| ||
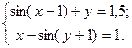 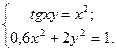
| 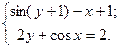 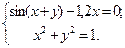
|
Рекомендации к выполнению лабораторной работы. Рассмотрим несколько примеров.
Пример 1. Найти корни полинома 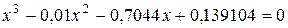 .
.
Для начала решим уравнение графически. Известно, что графическим решением уравнения f(x)=0 является точка пересечения графика функции f(x) с осью абсцисс, т.е. такое значение x,при котором функция обращается в ноль.
Проведем табулирование полинома на интервале от -1 до 1 с шагом 0,2. Функцию зададим формулой В2=A2^3-0,01*A2^2-0,7044*A2+0,139104. На графике видно (рис. 17), что функция три раза пересекает ось Оx, а так как полином третьей степени имеет не более трех вещественных корней, то графическое решение поставленной задачи найдено и определены интервалы[37], на которых находятся корни данного полинома: [-1,-0.8], [0.2,0.4] и [0.6,0.8].
|
|
Теперь можно найти корни полинома методом последовательных приближений с помощью команды Сервис®Подбор параметра [38]. В качестве начальных значений приближений к корням можно взять любые точки из отрезков локализации корней. Пусть это будут -0.9, 0.3 и 0.7. Введем эти значения в диапазон А14:А16, и вычислим для них значения функции по формуле
В14 =A14^3-0,01*A14^2-0,7044*A14+0,139104,
которую скопируем в ячейки В15 и В16 при помощи маркера заполнения.
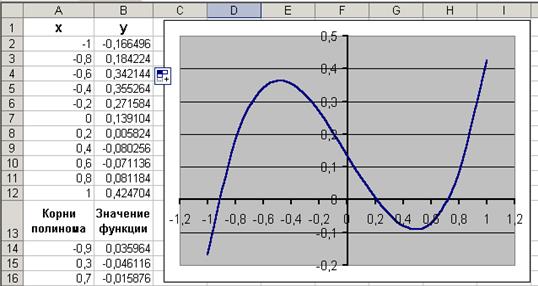
Рис. 18. Решение уравнения 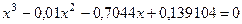
После ввода начальных приближений и значений функции можно обратиться к пункту меню Сервис®Подбор параметра и заполнить диалоговое окно так как показано на рис. 19.
В поле Установить в ячейке дается ссылка на ячейку в которую введена формула, вычисляющая значение левой части уравнения[39]. В поле Значение вводим правую часть уравнения, а в поле Изменяя значения ячейки дается ссылка на ячейку, отведенную под переменную[40]. После нажатия кнопки ОК появится диалоговое окно Результат подбора параметра с сообщением об успешном завершении поиска решения и приближенное значение корня будет помещено в ячейку А14. Два оставшихся корня находим аналогично. Результаты вычислений будут помещены в ячейки А15 и А16.
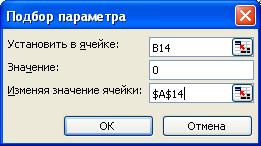
Рис. 19. Подбор параметра
Пример 2. Решить уравнение 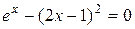 .
.
Проведем локализацию корней нелинейного уравнения. Для этого представим его в виде 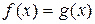 , т.е.
, т.е. 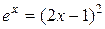 или
или 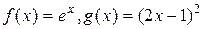 , и решим графически. Графическим решением уравнения
, и решим графически. Графическим решением уравнения 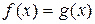 будет точка пересечения линий
будет точка пересечения линий 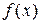 и
и 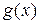 .
.
Построим графики 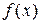 и
и 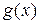 . Для этого в диапазон А3:А18 введем значения аргумента. Значение функции
. Для этого в диапазон А3:А18 введем значения аргумента. Значение функции 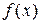 определим формулой В3=EXP(A3), а значение
определим формулой В3=EXP(A3), а значение 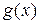 : С3=(2*A3-1)^2 (рис. 20).
: С3=(2*A3-1)^2 (рис. 20).
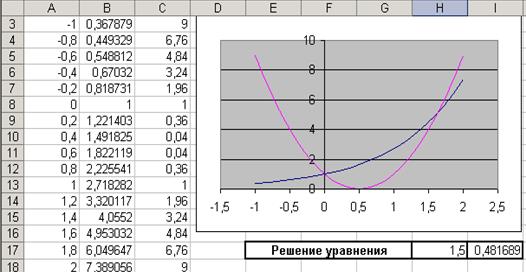
Рис. 20. Решение уравнения 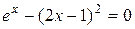
На графике видно, что линии 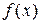 и
и 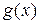 пересекаются дважды, т.е. данное уравнение имеет два решения. Одно из них тривиальное и равно нулю. Для второго можно определить интервал изоляции корня:
пересекаются дважды, т.е. данное уравнение имеет два решения. Одно из них тривиальное и равно нулю. Для второго можно определить интервал изоляции корня: 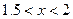 и уточнить его методом последовательных приближений. Введём начальное приближение в ячейку Н17=1.5, и зададим само уравнение:
и уточнить его методом последовательных приближений. Введём начальное приближение в ячейку Н17=1.5, и зададим само уравнение:
|
|
I17 =EXP(H17)-(2*H17-1)^2.
Далее воспользуемся пунктом меню Сервис®Подбор параметра и заполним диалоговое окно Подбор параметра. В поле Установить в ячейке вводим адрес функции I17. В поле Значение вводим правую часть уравнения, т.е. ноль. Поле Изменяя значения ячейки заполняется адресом переменной Н17. Результатпоиска решения будет выведен в ячейку Н17.
Пример 3. Решить систему уравнений
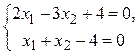 .
.
В MS Excel есть очень удобная операция – Поиск решения (рис. 21). Вообще говоря, она предназначена для решения задач оптимизации. Применим ее для решения системы уравнений, сведя задачу к задаче отыскания минимума функции.
Пусть в ячейках D1 и D2 [41] хранятся начальные значения переменных x1 и x2. В ячейки E1 и E2 введем уравнения системы:
E1=2*D1-3*D2+4, E2=D1+D2-4.
В качестве функции цели введем формулу
F1 = E1^2+E2^2 [42].
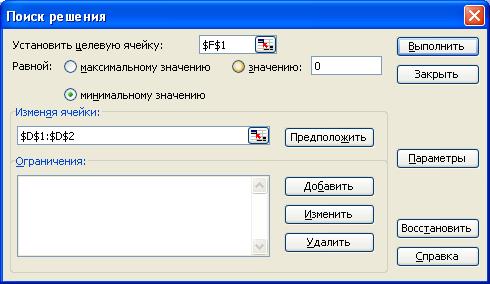
Рис. 21. Поиск решения системы уравнений
Обратимся к решающему блоку с помощью команды Сервис®Поиск решения и заполним диалоговое окно, так как показано на рис. 1.33[43]. Далее нажмем кнопку Выполнить и получаем решение системы в ячейках D1 и D2:
x1= 1,600000128, x2= 2,39999949.
[31] Чтобы добавить пустой столбец можно воспользоваться командами Вставка®Столбец или Добавить ячейки…®столбец.
[32] Функции СУММ и СРЗНАЧ можно ввести с клавиатуры или при помощи Мастера функций
[33] Маркер автозаполнения – черная точка в нижнем правом углу ячейки. При установке курсора в маркер автозаполнения он принимает вид черного перекрестия.
[34] Данные можно вводить, используя клавиатуру или выделив их на рабочем листе, удерживая левую кнопку мыши.
[35] В ячейке А1 первое значение аргумента, т.е. 5. В ячейке А2 – второе, оно равно -4,5. Выделяем диапазон А1:А2, устанавливаем курсор в маркер автозаполнения и удерживая левую кнопку мыши заполняем ячейки до А21. Последнее значение аргумента равно 5.
[36]
[37] Такие интервалы называют интервалами изоляции корней.
[38] Относительная погрешность вычислений и предельное число итераций (например, 0,00001 и 1000) задаются на вкладке Сервис®Параметры.
[39] Уравнение должно быть записано так, чтобы его правая часть не содержала переменную.
[40] Вводить ссылки на ячейки в поля диалогового окна Подбор параметров удобнее не с клавиатуры, а щелчком на соответствующей ячейке.
|
|
[41] Ячейки не заполняются и по умолчанию равны нулю. При желании можно решить задачу графически и ввести в качестве начальных приближений значения близкие к корням.
[42] Сумма квадратов заданных функций.
[43] Иначе говоря, необходимо найти минимум функции в ячейке F1, изменяя значения переменных из ячеек D1 и D2.
|
|
|

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!