Тема. Обработка данных с помощью электронных таблиц MS Excel.

Тема. Системы счисления.

Цель работы. Изучение арифметического и логического устройства компьютера. Знакомство с представлением информации в ПЭВМ. Приобретение навыков перевода из одной системы счисления (с/с) в другую.

Задание. Выполнить перевод из одной с/с в другую, сделать проверку (табл. 1).

Таблица 1. Варианты заданий.

№ п/п	X2®(?)10	Y2®(?)8, Y2®(?)16	Z10®(?)2, z10®(?)8, Z10®(?)16	S8®(?)16	U16®(?)8	Wp®(?)10	P
	11011,1101		235,647		6D3,2B
	11101,0011		417,813		95C,F7
	10101,1111		176,451		3D6,B5
	10001,1001		156,848		63D,C1
	10011,0001		601,003		34F,A8
	11001,1000		126,012		13A,DE
	11110,1000		325,632		D13,2B
	10111,0111		484,191		9E7,2D
	11100,1110		681,534		3CD,1E
	11000,1010		183,654		5CA,1E
	10100,1001		273,021		C3F,E7
	10010,0101		289,713		C1F,D5
	11111,0101		259,527		986,37
	10111,1111		201,113		689,37
	11111,1101		114,453		467,EA
	10101,0101		176,724		ADE,71
	11010,1001		106,398		E73,DE
	100010,011		982,754		D19,AB
	101101,011		417,983		BE7,D9
	100111,011		742,429		1CD,8E
	111011,001		659,832		5FA,1E
	101110,101		286,327		C38,97
	111001,011		687,321		C9F,D5
	10101,0101		945,325		9A6,B7
	110101,100		467,894		D89,F5
	10100,1010		395,532		469,FA
	10111,0111		984,291		8DE,7A
	110001,110		671,544		E79,8E
	11010,1111		883,154		6D8,BA
	111011,001		473,621		E5C,A4

Рекомендации к выполнению лабораторной работы. Назначение компьютера - следуя, поступающим от человека командам, принимать, перерабатывать, хранить и выдавать информацию. Проделывая сотни тысяч, миллионы операций в секунду, компьютер позволяет работать с текстами и графикой, слушать музыку, смотреть фильмы, работать в сети и многое другое. Но чем бы пользователь ни был занят, он посылает компьютеру команды, которые переводятся в вычислительные инструкции, «понятные» компьютеру, а затем выполняются. Поэтому возникает вопрос: как считает компьютер? Оказывается, чтобы научить вычислениям электронное устройство, были созданы специальные системы счисления.

Числа могут быть записаны в различных системах счисления. Наиболее привычна для нас десятичная система счисления, в которой принят счет десятками и используется 10 основных цифр (0,1,2,3,4,5,6,7,8,9). Размещая эти цифры на различных позиция, можно выразить любое число.

Например, рассмотрим число 743. Оно состоит из семи сотен, четырех десятков и трех единиц и представляет собой сумму цифр 700, 40 и 3. Значит, верной будет следующая запись:

(743)₁₀=700+40+3=7×10² +4×10¹ +3×10⁰=743,

где число представлено как сумма произведений некоторой десятичной цифры на соответствующую ее позиции степень числа 10, которое в свою очередь является основанием системы счисления.

В случае с правильной дробью получим:

(0,517)₁₀=0,5+0,01+0,007=5×10^-1 +1×10^-2 +7×10^-3=0,517;

По такому принципу можно построить систему счисления с произвольным основанием b.

Любое целое число N, заданное в b -ичной системе счисления, можно записать в развернутом виде:

,

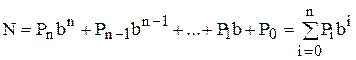
b – целое положительное фиксированное число (основание системы счисления);

P_i – целое число ( - называемое позиционной цифрой или разрядом.

Правильная дробь записывается в развернутом виде так:

, .

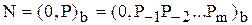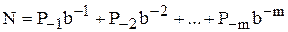Например,

(1203,0205)₁₀ =1×10^{3 +}2×10² +0×10¹ +3×10⁰+0×10^-1 +2×10^-2 +0×10^-3+5×10^-4=

=1000+200+0+3+0+0,02+0+0,0005=1203+0,0205=1203,0205.

Рассмотрим системы с основанием 2, 8, 16 и их связь с десятичной системой счисления.

Вычислительные машины могут быть построены на базе любой системы счисления, но наиболее естественным электронным способом счета является способ "есть сигнал / нет сигнала", поэтому в современных ЭВМ используется преимущественно двоичная система счисления, основанная на двух цифрах 0 и 1 (два состояния значительно легче различить, чем 10).

Рассмотрим на примерах как перевести двоичное число в более привычную десятичную систему счисления.

(101101)₂=1×2⁵+0×5⁴+1×2³+1×2²+0×5¹+1×2⁰=32+8+4+1=(45)₁₀

(10101,1101)₂=1×2⁴+0×2³+1×2²+0×2¹+1×2⁰ +1×2^-1+1×2^-2+0×2^-3+1×2^-4=

=16+4+1+1/2+1/4+1/16=21+13/16=(21,8125)₁₀

Существенным недостатком двоичной системы счисления является громоздкая запись чисел. Для упрощения записи двоичных чисел могут быть использованы восьмеричная и шестнадцатеричная системы счисления.

Таблица 2. Образцы записи чисел в различных системах счисления

ЧИСЛО
десятичное	двоичное	восьмеричное	двоичное	шестнадцатеричное
		-
		-
		-		A
		-		B
		-		C
		-		D
		-		E
		-		F

Двоичная система связана с восьмеричной и шестнадцатеричной соотношениями: 2³=8 и 2⁴=16, т.е. цифры восьмеричной системы можно представить двоичными триадами, шестнадцатеричной – тетрадами, что облегчает взаимный перевод.

Например, (110100101)₂®(110 100 101)₂®(645)₈ ;

(11011101)₂®(011 011 101)®(335)₈; (101111101111)₂®(1011 1110 1111)₂®(BEF)₁₆;

(10111011000)₂®(0101 1101 1000)₂®(5D8)₁₆

Вообще, для того чтобы перевести целое число из одной системы счисления в другую необходимо выполнить следующие действия:

1) поделить данное число на основание новой системы счисления;

2) перевести остаток от деления в новую систему счисления; получается младший разряд нового числа;

3) если частное от деления больше основания новой системы, продолжать деление, как указано в п.1; новый остаток, переведенный в новую систему счисления, дает второй разряд числа и т.д.

Пример. Перевести число 256 из десятичной системы счисления в восьмеричную. (Далее, будем записывать кратко (256)₁₀®(?)₈)

Решение.

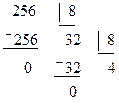
Ответ. (256)₁₀®(400)₈.

Проверка: (400)₈=4×8²+0×8¹+0×8⁰=256+0+0=(256)₁₀

Пример. Пусть необходимо выполнить перевод (397)₁₀®(?)₁₆

Решение:

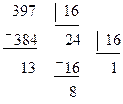
Ответ: (397) ₁₀®(18D)₁₆.

Проверка: (18D)₁₆=1×16²+8×16¹+13×16⁰=256+128+13=(397)₁₀

Пример. Выполнить преобразование (25) ₁₀®(?)₂

Решение:

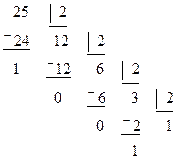
Ответ: (25) ₁₀®(11001)₂. Проверка: (25)₁₀=1×2⁴+1×2³+0×2²+0×2¹ +1×2⁰=16+8+1=(25)₁₀

Правило перевода дробей из одной системы счисления в другую заключается в выполнении следующих действий:

1) умножить дробную часть числа на основание системы счисления;

2) в полученном произведении выделить целую часть числа (это будет старшим разрядом искомого числа);

3) дробную часть произведения снова умножить на основание новой системы счисления; целая часть произведения будет следующим разрядом дробной части искомого числа;

4) п.3 повторить до получения необходимого количества разрядов искомого числа.

Пример. Выполнить перевод (0,784)₁₀ ®(?)₂, 0,6125₁₀ ®(?)₈ и (0,378)₁₀ ®(?)₁₆. Оставить четыре знака после запятой.

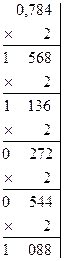
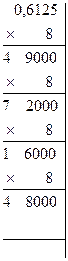
Результат получаем, читая цифры сверху вниз:

(0,784)₁₀ ®(0,1100)₂

0,6125₁₀ ®(0,4714)₈

(0,378)₁₀ ®(0,60С4)₁₆.

Для перевода из одной системы в другую смешанного числа необходимо отдельно выполнить перевод целой и дробной его частей по рассмотренным выше правилам.

Лабораторная работа №2

Таблица 3. Варианты заданий (продолжение).

№4	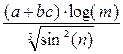№5	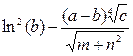№6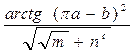
	I	II	III		I	II	III		I	II	III
a	23.16	17.41	32.37	a	22.16	15.71	12.31	a	16.342	12.751	31.456
b	8.32	1.27	2.35	b	5.03	3.28	1.73	b	2.5	3.7	7.3
c	145.5	342.3	128.7	c	3.6	7.2	3.7	c
m	28.6	11.7	27.3	m	12.37	13.752	17.428	m	9.14	8.12	6.71
n	0.28	0.71	0.93	n	86.2	33.7	41.7	n	3.6	1.7	5.8
№7	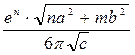№8	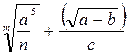№9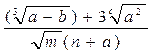
	I	II	III		I	II	III		I	II	III
a	23.16	17.41	32.37	a	16.342	12.751	31.456	a	10.82	9.37	11.45
b	8.32	1.27	2.35	b	14.32	10.324	29.678	b	2.786	3.108	4.431
c	145.5	342.3	128.7	c	38.17	23.76	33.28	c
m	28.6	11.7	27.3	m				m	0.28	0.46	0.75
n	0.28	0.71	0.93	n	3.6	1.7	5.8	n	14.7	15.2	16.7
№10	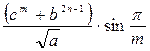№11	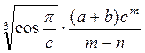№12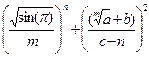
	I	II	III		I	II	III		I	II	III
a	2.0435	1.1752	4.5681	a	5.3	6.2		a	12.5	19.5	12.8
b	4.2	3.8	6.3	b	18.21	16.32	23.16	b	3.2	5.9	7.2
c	1.2	5.7	2.99	c				c	4.22	3.49	5.82
m				m	13.417	20.863	17.925	m
n				n	8.371	7.562	8.134	n	23.722	14.782	11.232
№13	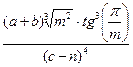№14	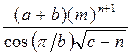№15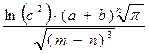
	I	II	III		I	II	III		I	II	III
a	3.754	4.236	5.523	a	25.16	16.41	12.37	a	22.16	15.71	12.31
b	11.3	14.8	10.5	b	8.52	1.67	2.25	b	5.03	3.28	1.73
c	0.63	0.64	0.85	c	143.5	356.3	124.7	c	3.6	7.2	3.7
m				m	28.7	14.6	26.3	m
n	6.32	7.15	4.15	n				n
№16	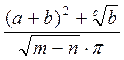№17	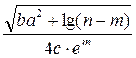№18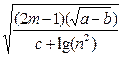
	I	II	III		I	II	III		I	II	III
a	16.342	12.751	31.456	a	23.16	17.41	32.37	a	16.342	12.751	31.456
b	2.5	3.7	7.3	b	8.32	1.27	2.35	b	2.5	3.7	7.3
c				c	145.5	342.3	128.7	c	38.17	23.76	33.28
m	9.14	8.12	6.71	m				m
n	3.6	1.7	5.8	n				n	3.6	1.7	5.8

 

Таблица 3. Варианты заданий (продолжение).

№19	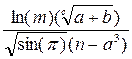№20	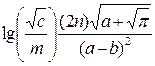№21
	I	II	III		I	II	III		I	II	III
a	10.82	9.37	11.45	a	2.0435	1.1752	4.5681	a	4.3	5.2	2.13
b	2.786	3.108	4.431	b	4.2	3.8	6.3	b	17.21	15.32	22.16
c				c				c
m	0.28	0.46	0.75	m	3.6	1.7	5.8	m	12.417	21.823	16.825
n	14.7	15.2	16.7	n				n	8.37	7.56	8.13
№22	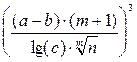№23	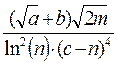№24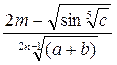
	I	II	III		I	II	III		I	II	III
a	13.5	18.5	11.8	a	2.754	3.236	4.523	a	23.16	17.41	32.37
b	3.7	5.6	7.4	b	11.7	15.8	10.8	b	8.32	1.27	2.35
c	4.22	3.42	5.82	c	0.65	0.65	0.85	c	145.5	342.3	128.7
m				m				m	28.6	11.7	27.3
n	23.725	14.782	11.234	n	6.32	7.18	4.17	n
№25	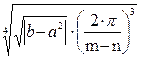№26	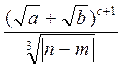№27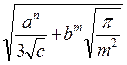
	I	II	III		I	II	III		I	II	III
a	22.16	15.71	12.31	a	16.342	12.751	31.456	a	23.16	17.41	32.37
b	5.03	3.28	1.73	b	2.5	3.7	7.3	b	8.32	1.27	2.35
c	3.6	7.2	3.7	c				c	145.5	342.3	128.7
m				m	9.14	8.12	6.71	m
n				n	6.35	7.06	5.8	n
№28	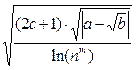№29	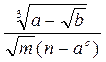№30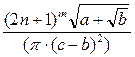
	I	II	III		I	II	III		I	II	III
a	16.342	12.751	31.456	a	10.82	9.37	11.45	a	2.0435	1.1752	4.5681
b	2.5	3.7	7.3	b	2.786	3.108	4.431	b	4.2	3.8	6.3
c	38.17	23.76	33.28	c	0.5	0.6	0.7	c	3.6	7.2	3.7
m				m	0.28	0.46	0.75	m
n	3.6	1.7	5.8	n	14.7	15.2	16.7	n

 

Рекомендации к выполнению лабораторной работы.

Рассмотрим решение данной задачи на примере 12-го варианта. Введем исходные данные на первый рабочий лист MS Excel (рис. 1). Для того чтобы можно было добавить к полученной таблице заголовок, необходимо вначале добавить пустую строку. Установим курсор в ячейку А1 и выполним команду Вставка®Строки или команду контекстного меню Добавить ячейки…, это приведет к появлению окна изображенного на рис. 2[31].

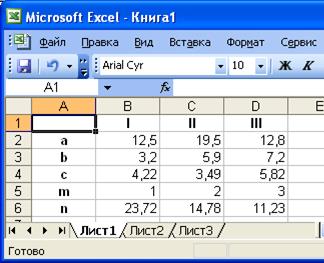
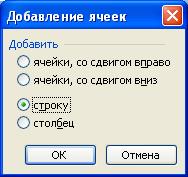
Рис. 1. Ввод данных в рабочий лист MS Excel Рис. 2. Добавление строки

Введем фразу «Лабораторная работа» в ячейку А1, которая теперь свободна, т.к. вся таблица сместилась вниз на одну строку. Для оформления заголовка выделим ячейки А1:D1 (рис. 3). Затем выполним команду Формат® Ячейки® Выравнивание и установим опции Объединение ячеек и По центру, либо воспользоваться соответствующими кнопками на панели инструментов. Изменение шрифта осуществляется с помощью пункта меню Формат® Ячейки…®Шрифт, либо с помощью кнопок Полужирный, Курсив, Подчеркивание на панели инструментов. Изменение цвета шрифта и фона выполняется с помощью пункта меню Формат® Ячейки…®Шрифт, Формат® Ячейки…®Вид, либо с помощью кнопок Цвет заливки, Цвет шрифта на панели инструментов. Изменение типа, фона и цвета шрифта происходит в текущей ячейке или в выделенной области. Например, в нашем случае, для изменения типа шрифта необходимо выделить диапазон A1:D2 и воспользоваться кнопкой Полужирный, затем выделить диапазон А3:А7 и нажать кнопку Курсив. Для обрамления таблицы необходимо выделить всю таблицу и в контекстном меню выбрать пункт Формат ячеек…, а в открывшемся диалоговом окне вкладку Граница, либо воспользоваться кнопкой Границы на панели инструментов.

Переименование листа осуществляют командой главного меню Формат®Лист®Переименовать или, вызывают команду контекстного меню Переименовать, щелкнув правой кнопкой мыши на ярлыке листа.

Копирование таблицы на другой лист рабочей книги выполним так. Выделим диапазон A1:D7 и выполним команду контекстного меню Копировать. Затем перейдем на Лист 2, щелкнув по ярлыку листа левой кнопкой мыши. На втором листе установим курсор в ячейку А1 и выполним команду контекстного меню Вставить.

Чтобы вычислить значения F, S и SR для первого набора данных в ячейки А8:А10 введем соответствующие имена переменных (рис. 3). Затем введем следующие формулы:

· для вычисления значения F по заданной формуле

В8=(SIN(ПИ()^0,5/B6))^B7+((B3^(1/B6)+B4)/(B5-B7))^2,

· для вычисления суммы значений первого набора данных

В9=СУММ(B3:B7),

· для вычисления среднего значения первого набора данных[32]

В10=СРЗНАЧ(B3:B7).

Вычисление значений F, S и SR для двух других наборов данных произойдет автоматически, если формулы из ячеек В8, В9 и В10 скопировать в следующие по строке ячейки. Сделать это можно при помощи маркера автозаполнения[33]. Например, для копирования формулы изячейки В8, ее необходимо выделить, затем установить курсор в маркер автозаполнения и удерживая левую кнопку мыши заполнить необходимый диапазон, в нашем случае это ячейки С8 и D8. Копирование формул из ячеек В9 и В10 происходит аналогично.

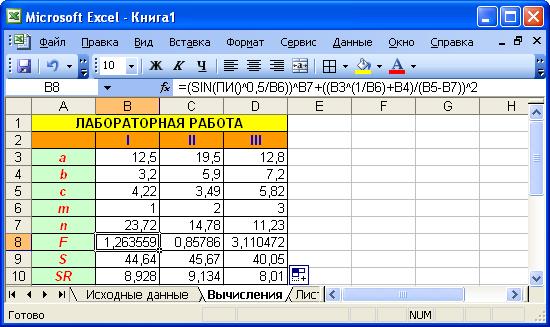
Рис. 3. Решение задачи из варианта 12

Изменить размер шрифта в диапазоне А8:D10 можно, если выделить его и воспользовавшись командой главного меню Формат®Ячейки…®Шрифт или выбрать нужный размер шрифта на панели инструментов.

Для сохранения книги выполним команду Файл®Сохранить или нажмем соответствующую кнопку на панели инструментов.

Лабораторная работа №3

Задание. Решить следующие задачи.

1. Найти решение системы линейных алгебраических уравнений с помощью обратной матрицы, выполнить проверку.

2. Найти решение системы линейных уравнений методом Крамера.

3. Выполнить действия над матрицами.

 

Вариант №1 1) 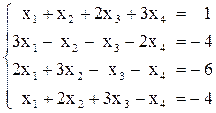2)

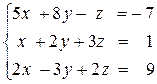
3) 2 (A + B) (2B – A),

Вариант №2 1) 2)

3) 3 A - (A + 2B) B,

Вариант № 3 1) 2)

3) 2(A–B)(A² + B),

Вариант №4 1) 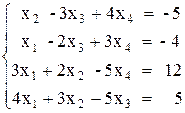2)

3) (A² – B²)(A + B),

Вариант №5 1) 2)

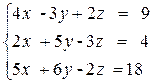
3) (A–B²)(2A+B),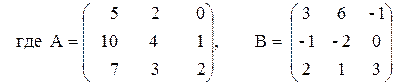

Вариант №6 1) 2)

3) (A – B) A + 2B,

Вариант №7 1) 2)

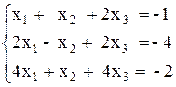
3) 2(A–0,5B)+AB,

Вариант №8 1) 2)

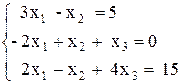
3) (A – B)A + 3B,

Вариант №9 1) 2)

3) 2A – (A² + B) B,

Вариант №10 1) 2)

3) 3 (A² – B²) –2АB,

Вариант №11 1) 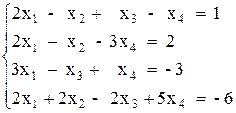2)

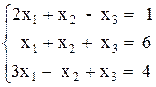
3) (2A–B)(3А+B)–2АВ,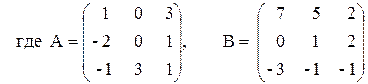

Вариант №12 1) 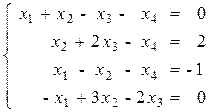2)

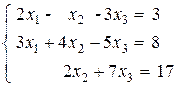
3) А(A²–B)-2(B+А)В,

Вариант №13 1) 2)

3) (A+B)A–B(2А+3В),

Вариант №14 1) 2)

3) A(2A+B)–B(А–В),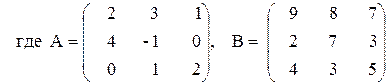

Вариант №15 1) 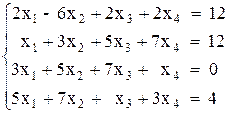2)

3) 3(A+B)(AВ–2А),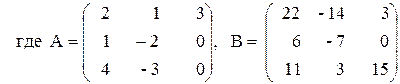

Вариант №16 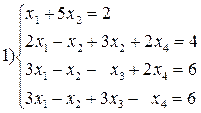2)

3) где

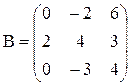
Вариант №17 1) 2)

3) 2А + 3B(АB-2А),

Вариант №18 1) 2)

3)

Вариант №19 1) 2)

3) 2A - АB(В - А) + В,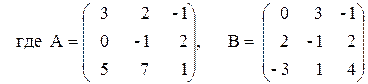

Вариант №20 1) 2)

3) A² - (A + B)–(А – 3В),

Вариант №21 1) 2)

3)

Вариант№22

Вариант №23 1) 2)

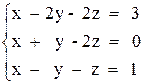
3) А(A - B) + 2В(A + В),

Вариант№24 1) 2)

Вариант№25

Вариант №26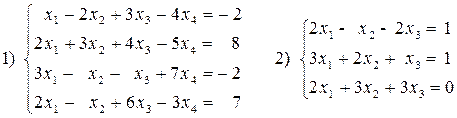

Вариант №27

Вариант №28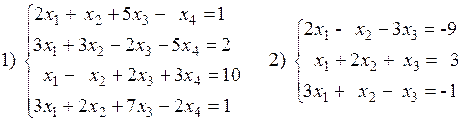

Вариант№29

Вариант №30

 

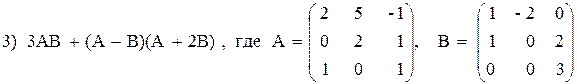
Рекомендации к выполнению лабораторной работы.

Предварительно вспомним некоторые сведения из курса высшей математики, необходимые для выполнения данной лабораторной работы.

Решение систем линейных алгебраических уравнений (СЛАУ).

Пусть задана СЛАУ следующего вида:

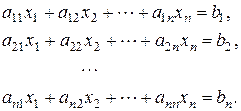
Эту систему можно представить в матричном виде: AX=b, где

– матрица коэффициентов системы уравнений;

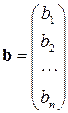– вектор неизвестных, – вектор правых частей.

При выполнении лабораторной работы систему линейных алгебраических уравнений необходимо будет решать методом обратной матрицы и методом Крамера. Вспомним основные формулы, используемые в этих методах.

Метод обратной матрицы.

Систему линейных алгебраических уравнений Ax=b умножим слева на матрицу, обратную к А. Система уравнений примет вид:

A^-1.A^.x=A^-1.b, E^.x=A^-1.b, (E – единичная матрица)

Таким образом, вектор неизвестных вычисляется по формуле x=A^-1.b.

Метод Крамера.

В этом случае неизвестные x₁,x₂,…, x_n вычисляются по формуле:

где D – определитель матрицы A, D_i – определитель матрицы, получаемой из матрицы А путем замены i-го столбца вектором b.

 

Рассмотрим несколько примеров. Обратите внимание на особенность работы с матричными функциями в Ms Excel: необходимо предварительно выделять область, в которой будет храниться результат, а после получения результата преобразовывать его к матричному виду, нажав клавиши F2 и Ctrl+Shift+Enter.

Пример 1. Решить систему методом обратной матрицы:

Идея решение СЛАУ методом обратной матрицы заключается в следующем. Заданную систему записывают в матричной форме Ax=b, где A – матрица коэффициентов СЛАУ при неизвестных, b – вектор правых частей, x – вектор неизвестных, который вычисляют по формуле x=A^-1.b, причем A^-1. – это матрица обратная к A. Реализовать эту идею в MS Excel можно следующим образом. Введём матрицу A и вектор b в рабочий лист MS Excel (Рис. 11). Пусть матрица А находится в ячейках B1:D3, а вектор b в диапазоне F1:F3. Выделим ячейки для хранения обратной матрицы, пусть это будут ячейки B5:D7.

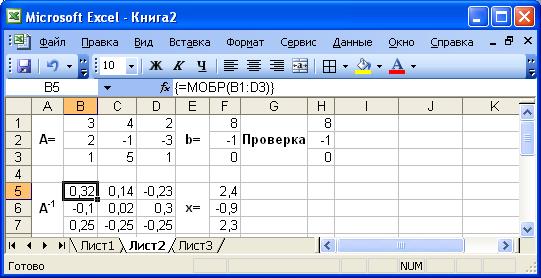
Рис. 11. Решение СЛАУ методом обратной матрицы

Обратимся к Мастеру функций, и в категории Математические выберем функцию МОБР, предназначенную для вычисления обратной матрицы. В качестве аргумента этой функции укажем диапазон ячеек, в котором хранится матрица A, т.е. МОБР(B1:D3) [34]. Теперь умножим полученную обратную матрицу на вектор b. Выделим ячейки для хранения результирующего вектора, например F5:F7. Обратимся к Мастеру функций, и в категории Математические выберем функцию МУМНОЖ, которая предназначена для умножения матриц. У этой функции два аргумента – диапазоны перемножаемых матриц. Введем в качестве первого аргумента диапазон ячеек, в котором содержится обратная матрица, а в качестве второго – ячейки, содержащие вектор b, т.е. МУМНОЖ (B5:D7;F1:F3). Вектор неизвестных хранится в ячейках F5:F7. Для того чтобы проверить, правильно ли решена система уравнений, необходимо умножить матрицу A на вектор x иполучить в результате вектор b. Умножение матрицы A на вектор x осуществляется при помощи функции МУМНОЖ(B1:D3; F5:F7).

Пример 2. Решить систему из примера 2 методом Крамера.

В этом случае неизвестные x₁,x₂,…, x_n вычисляются по формуле:

где D – определитель матрицы A, D_i – определитель матрицы, получаемой из матрицы А путем замены i-го столбца вектором b.

Введём матрицу А и вектор b в рабочий лист. Сформируем три вспомогательные матрицы, заменяя последовательно столбцы матрицы A на вектор b ( Рис. 12). Вычислим определитель матрицы A. Установим курсор в ячейку B5 и обратимся к мастеру функций. В категории Математические выберем функцию МОПРЕД, предназначенную длявычисления определителя матрицы. В качестве аргумента зададим диапазон ячеек, в котором хранится матрица A:

МОПРЕД(B1:D5).

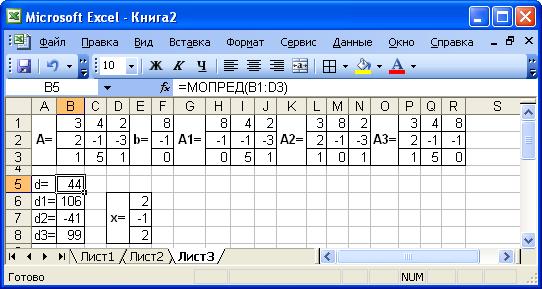
Рис. 12. Решение СЛАУ по формулам Крамера

Для вычисления вспомогательных определителей введем формулы:

B6=МОПРЕД(H1:J3), B7=МОПРЕД(L1:N3), B8=МОПРЕД(P1:R3).

В результате в ячейке B5 хранится главный определитель, а в ячейках B6: B8 – вспомогательные. Проведем вычисление по формулам Крамера. В ячейку Е6 введём формулу = Е6/$B$5. Затем скопируем её содержимое в ячейки Е7 и Е8. Система решена.

Пример 3. Вычислить матрицу С по формуле: C=A²+2AB, где

Решение задачи показано на Рис. 13.

Рис. 13. Матричные операции

Лабораторная работа №4

Задание.

1. Построить верхнюю (четные варианты) или нижнюю (нечетные варианты) часть эллипсоида, заданного уравнением . Варианты заданий представлены в табл. 9.

2. Построить однополостный (четные варианты) или двухполостный (нечетные варианты) гиперболоид, заданный уравнением . Знак плюс относится к уравнению однополостного гиперболоида, знак минус – к уравнению двухполостного гиперболоида. Варианты заданий представлены в табл. 10.

3. Построить эллиптический (четные варианты) или гиперболический (нечетные варианты) параболоид, заданного уравнением . Знак плюс относится к уравнению эллиптического параболоида, знак минус – к уравнению гиперболического параболоида. Варианты заданий представлены в табл.11.

Таблица 9. Варианты заданий

№	a	b	с	№	a	b	c
					3.1	3.2	5.3
		0.9	1.1		1.25	1.95	1.5
					1.5	1.25	1.95
	0.71	0.75	1.21
	1.72	2.9	3.1
	5.71	4.75	4.21		7.1	7.5	4.21
	2.72	3.9	5.1		7.2	8.9
	1.5	0.78	1.45		1.5	2.78	3.45

 

Таблица 10. Варианты заданий

№	a	b	с	№	a	b	c