Пара (X, Y) – где X и Y – случайные величины, называется системой двух случайных величин. Если X и Y – дискретные случайные величины, то законом распределения системы двух случайных величин (X, Y) является множество всех пар 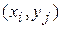 возможных значений величин X и Y и вероятностей
возможных значений величин X и Y и вероятностей 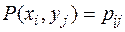 их совместного появления. Такой закон удобно задавать в виде таблицы, которая носит название таблицы распределения двумерной случайной величины (X, Y).
их совместного появления. Такой закон удобно задавать в виде таблицы, которая носит название таблицы распределения двумерной случайной величины (X, Y).
События, состоящие в том, что случайная величина Х примет значение 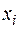 (i = 1, 2, …, n), а случайная величина Y примет значение
(i = 1, 2, …, n), а случайная величина Y примет значение 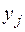 (j = 1, 2, …, m), несовместны и единственно возможны, т.е. образуют полную группу попарно несовместных событий, поэтому сумма всех вероятностей таблицы равна единице:
(j = 1, 2, …, m), несовместны и единственно возможны, т.е. образуют полную группу попарно несовместных событий, поэтому сумма всех вероятностей таблицы равна единице: 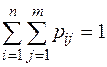 .
.
| Y
| X
|
| x 1
| x 2
| …
| xn
|
| y 1
| P (x 1, y 1)
| P (x 2, y 2)
| …
| P (xn, y 1)
|
| …
| …
| …
| …
| …
|
| ym
| P (x 1, ym)
| P (x 2, ym)
| …
| P (xn, ym)
|
По закону распределения двумерной случайной величины (X, Y) можно найти законы распределения каждой случайной величины X и Y. Для того, чтобы найти вероятность 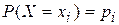 того, что случайная величина Х примет значение
того, что случайная величина Х примет значение 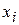 , надо просуммировать вероятности столбца
, надо просуммировать вероятности столбца 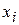 :
: 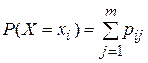 . Аналогично, для того, чтобы найти вероятность
. Аналогично, для того, чтобы найти вероятность 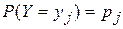 того, что случайная величина Y примет значение
того, что случайная величина Y примет значение 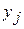 , надо просуммировать вероятности строки
, надо просуммировать вероятности строки 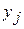 :
:  .
.
Вероятность 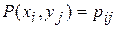 — это вероятность того, что случайная величина Х примет значение
— это вероятность того, что случайная величина Х примет значение 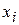 , а случайная величина Y примет значение
, а случайная величина Y примет значение 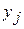 . Эту вероятность по теореме умножения вероятностей можно записать в виде:
. Эту вероятность по теореме умножения вероятностей можно записать в виде:  . Из этого равенства можно получить формулы:
. Из этого равенства можно получить формулы:
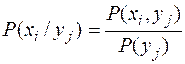 ,
,  .
.
Функцией распределения системы двух случайных величин (X, Y) называется вероятность совместного выполнения двух неравенств Х < х, Y < y:
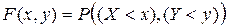 .
.
Условным математическим ожиданием дискретной случайной величины Y при 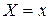 называется число, обозначаемое
называется число, обозначаемое 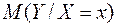 и вычисляемое по формуле:
и вычисляемое по формуле:
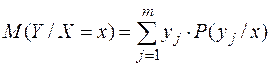 .
.
Функцию 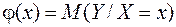 , как функцию аргумента x, называют функцией регрессии Y на X.
, как функцию аргумента x, называют функцией регрессии Y на X.
Условным математическим ожиданием дискретной случайной величины Х при 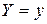 называется число, обозначаемое
называется число, обозначаемое 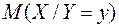 и вычисляемое по формуле:
и вычисляемое по формуле:
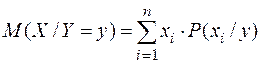 .
.
Функцию 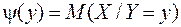 , как функцию аргумента y, называют функцией регрессии X на Y.
, как функцию аргумента y, называют функцией регрессии X на Y.
Корреляционным моментом (или ковариацией) случайных величин X и Y называется математическое ожидание произведения отклонений этих величин от их математических ожиданий:
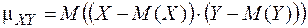 .
.
Корреляционный момент можно найти по формуле:
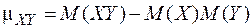 .
.
Для независимых случайных величин X и Y 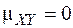 .
.
Для дискретных случайных величин X и Y корреляционный момент равен:
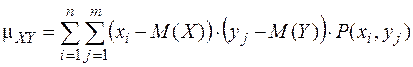 .
.
Коэффициентом корреляции случайных величин X и Y называется безразмерная величина:
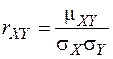 ,
,
где 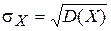 ,
, 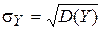 .
.
Свойства коэффициента корреляции
1. Коэффициент корреляции характеризует тесноту и направление корреляционной связи.
2.  ;
;
3. Если Х и Y — независимые случайные величины, то коэффициент корреляции равен 0.
4. Если 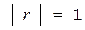 , то между величинами Х и Y имеет место функциональная зависимость, а именно, линейная. Отсюда следует, что коэффициент корреляции измеряет тесноту линейной связи между величинами Х и Y.
, то между величинами Х и Y имеет место функциональная зависимость, а именно, линейная. Отсюда следует, что коэффициент корреляции измеряет тесноту линейной связи между величинами Х и Y.
5. Если 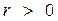 , то связь между величинами прямая (положительная корреляция), т.е. при увеличении значений одного признака значения другого признака увеличиваются. Если
, то связь между величинами прямая (положительная корреляция), т.е. при увеличении значений одного признака значения другого признака увеличиваются. Если 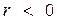 , то связь обратная (отрицательная корреляция), т.е. при увеличении значений одного признака значения другого признака уменьшаются.
, то связь обратная (отрицательная корреляция), т.е. при увеличении значений одного признака значения другого признака уменьшаются.
6. Если 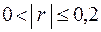 , то корреляционная связь очень слабая;
, то корреляционная связь очень слабая;
если 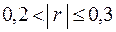 , то корреляционная связь слабая;
, то корреляционная связь слабая;
если 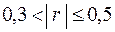 , то корреляционная связь умеренная;
, то корреляционная связь умеренная;
если 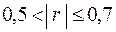 , то корреляционная связь умеренная;
, то корреляционная связь умеренная;
если  , то корреляционная связь тесная или сильная.
, то корреляционная связь тесная или сильная.
Две случайные величины называются коррелированными, если их коэффициент корреляции отличен от нуля, и некоррелированными, если он равен нулю.
При рассмотрении двумерной случайной величины (X, Y), где X и Y – зависимые случайные величины, используются различные приближения одной случайной величины с помощью другой. Важнейшим из них является линейное приближение.
Представим случайную величину Y в виде линейной функции величины Х:
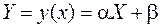 ,
,
где α и β – параметры, подлежащие определению. Если числа a и b подобраны так, что величина 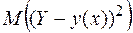 будет наименьшей, то числовая функция
будет наименьшей, то числовая функция 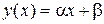 называется линейной средней квадратической регрессией Y на X. Нахождение такой прямой называют наилучшим приближением Y по методу наименьших квадратов. Коэффициент a называется коэффициентом регрессии Y на X. Известно, что
называется линейной средней квадратической регрессией Y на X. Нахождение такой прямой называют наилучшим приближением Y по методу наименьших квадратов. Коэффициент a называется коэффициентом регрессии Y на X. Известно, что
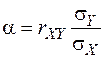 ,
, 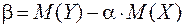 .
.
Уравнение 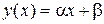 с учетом предыдущих формул можно записать в виде:
с учетом предыдущих формул можно записать в виде:
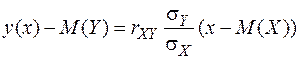 .
.
Аналогично, уравнение 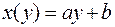 называется линейной средней квадратической регрессией X на Y записывается в виде:
называется линейной средней квадратической регрессией X на Y записывается в виде:
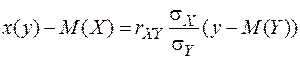 ,
,
где 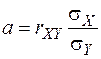 ,
, 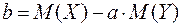 .
.
Задача. Система дискретных случайных величин задана таблицей:
Найти:
1) корреляционный момент;
2) коэффициент корреляции;
3) функцию линейной регрессии Y на X;
4) функцию линейной регрессии X на Y.
Решение. 1) Корреляционный момент находится по формуле 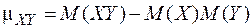 .
.
 ;
; 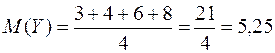 ;
;
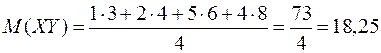 ;
;
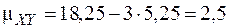 .
.
2) По формуле 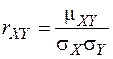 .
.
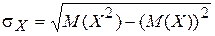 ;
;
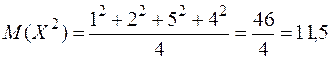 ;
; 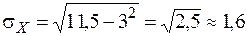 ;
;
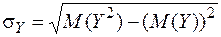 ;
;
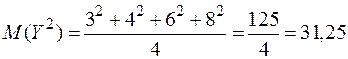 ;
;
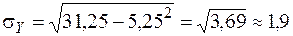 ;
;
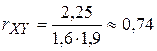 .
.
Коэффициент корреляции близок к единице, между случайными величинами существует тесная корреляционная зависимость.
3) Найдем коэффициенты функции регрессии Y на X:
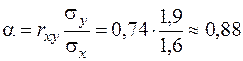 ;
;
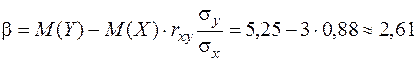 .
.
Функция регрессии Y на X имеет вид: 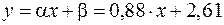 .
.
4) Найдем коэффициенты функции регрессии X на Y:
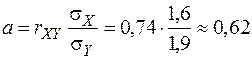 ;
;
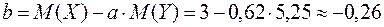 .
.
Функция регрессии X на Y имеет вид:  .
.
Задания для контрольной работы
Слушатель выполняет те задачи, номера которых находятся в следующей таблице, в соответствии с последней цифрой номера зачетной книжки.
Таблица заданий контрольной работы
| Последняя цифра
номера
зачетной книжки
| Номер задачи контрольной работы
|
|
| 1.1
| 2.1
| 3.1
| 4.1
| 5.1
| 6.1
| 7.1
| 8.1
|
|
| 1.2
| 2.2
| 3.2
| 4.2
| 5.2
| 6.2
| 7.2
| 8.2
|
|
| 1.3
| 2.3
| 3.3
| 4.3
| 5.3
| 6.3
| 7.3
| 8.3
|
|
| 1.4
| 2.4
| 3.4
| 4.4
| 5.4
| 6.4
| 7.4
| 8.4
|
|
| 1.5
| 2.5
| 3.5
| 4.5
| 5.5
| 6.5
| 7.5
| 8.5
|
|
| 1.6
| 2.6
| 3.6
| 4.6
| 5.6
| 6.6
| 7.6
| 8.6
|
|
| 1.7
| 2.7
| 3.7
| 4.7
| 5.7
| 6.7
| 7.7
| 8.7
|
|
| 1.8
| 2.8
| 3.8
| 4.8
| 5.8
| 6.8
| 7.8
| 8.8
|
|
| 1.9
| 2.9
| 3.9
| 4.9
| 5.9
| 6.9
| 7.9
| 8.9
|
|
| 1.10
| 2.10
| 3.10
| 4.10
| 5.10
| 6.10
| 7.10
| 8.10
|



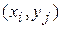 возможных значений величин X и Y и вероятностей
возможных значений величин X и Y и вероятностей 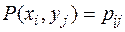 их совместного появления. Такой закон удобно задавать в виде таблицы, которая носит название таблицы распределения двумерной случайной величины (X, Y).
их совместного появления. Такой закон удобно задавать в виде таблицы, которая носит название таблицы распределения двумерной случайной величины (X, Y).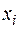 (i = 1, 2, …, n), а случайная величина Y примет значение
(i = 1, 2, …, n), а случайная величина Y примет значение 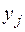 (j = 1, 2, …, m), несовместны и единственно возможны, т.е. образуют полную группу попарно несовместных событий, поэтому сумма всех вероятностей таблицы равна единице:
(j = 1, 2, …, m), несовместны и единственно возможны, т.е. образуют полную группу попарно несовместных событий, поэтому сумма всех вероятностей таблицы равна единице: 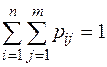 .
.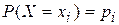 того, что случайная величина Х примет значение
того, что случайная величина Х примет значение 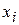 , надо просуммировать вероятности столбца
, надо просуммировать вероятности столбца 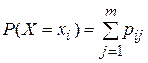 . Аналогично, для того, чтобы найти вероятность
. Аналогично, для того, чтобы найти вероятность 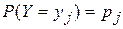 того, что случайная величина Y примет значение
того, что случайная величина Y примет значение 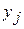 , надо просуммировать вероятности строки
, надо просуммировать вероятности строки  .
.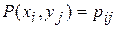 — это вероятность того, что случайная величина Х примет значение
— это вероятность того, что случайная величина Х примет значение  . Из этого равенства можно получить формулы:
. Из этого равенства можно получить формулы: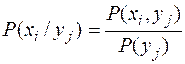 ,
,  .
.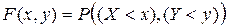 .
.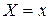 называется число, обозначаемое
называется число, обозначаемое 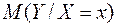 и вычисляемое по формуле:
и вычисляемое по формуле: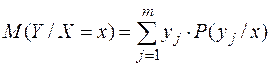 .
.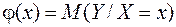 , как функцию аргумента x, называют функцией регрессии Y на X.
, как функцию аргумента x, называют функцией регрессии Y на X.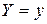 называется число, обозначаемое
называется число, обозначаемое 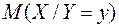 и вычисляемое по формуле:
и вычисляемое по формуле: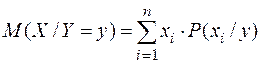 .
.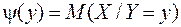 , как функцию аргумента y, называют функцией регрессии X на Y.
, как функцию аргумента y, называют функцией регрессии X на Y.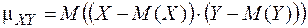 .
.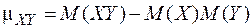 .
.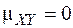 .
.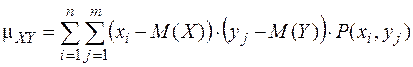 .
.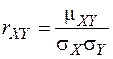 ,
,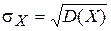 ,
, 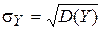 .
. ;
;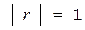 , то между величинами Х и Y имеет место функциональная зависимость, а именно, линейная. Отсюда следует, что коэффициент корреляции измеряет тесноту линейной связи между величинами Х и Y.
, то между величинами Х и Y имеет место функциональная зависимость, а именно, линейная. Отсюда следует, что коэффициент корреляции измеряет тесноту линейной связи между величинами Х и Y.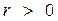 , то связь между величинами прямая (положительная корреляция), т.е. при увеличении значений одного признака значения другого признака увеличиваются. Если
, то связь между величинами прямая (положительная корреляция), т.е. при увеличении значений одного признака значения другого признака увеличиваются. Если 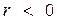 , то связь обратная (отрицательная корреляция), т.е. при увеличении значений одного признака значения другого признака уменьшаются.
, то связь обратная (отрицательная корреляция), т.е. при увеличении значений одного признака значения другого признака уменьшаются.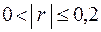 , то корреляционная связь очень слабая;
, то корреляционная связь очень слабая;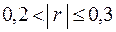 , то корреляционная связь слабая;
, то корреляционная связь слабая;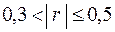 , то корреляционная связь умеренная;
, то корреляционная связь умеренная;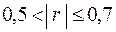 , то корреляционная связь умеренная;
, то корреляционная связь умеренная; , то корреляционная связь тесная или сильная.
, то корреляционная связь тесная или сильная.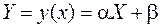 ,
,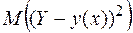 будет наименьшей, то числовая функция
будет наименьшей, то числовая функция 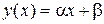 называется линейной средней квадратической регрессией Y на X. Нахождение такой прямой называют наилучшим приближением Y по методу наименьших квадратов. Коэффициент a называется коэффициентом регрессии Y на X. Известно, что
называется линейной средней квадратической регрессией Y на X. Нахождение такой прямой называют наилучшим приближением Y по методу наименьших квадратов. Коэффициент a называется коэффициентом регрессии Y на X. Известно, что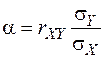 ,
, 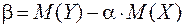 .
.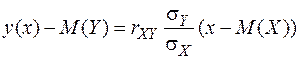 .
.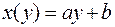 называется линейной средней квадратической регрессией X на Y записывается в виде:
называется линейной средней квадратической регрессией X на Y записывается в виде: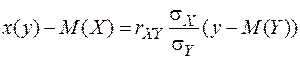 ,
,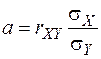 ,
, 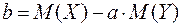 .
. ;
; 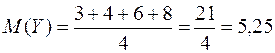 ;
;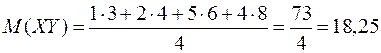 ;
;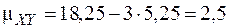 .
.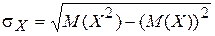 ;
;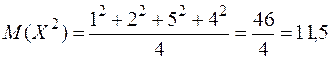 ;
; 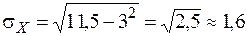 ;
;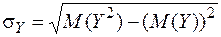 ;
;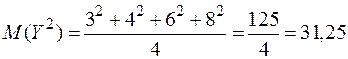 ;
;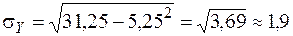 ;
;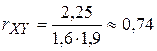 .
.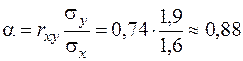 ;
;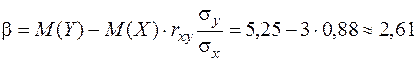 .
.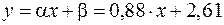 .
.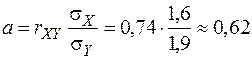 ;
;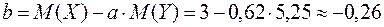 .
. .
.


