Многофакторный корреляционно-регрессионный анализ

В экономических исследованиях результативный признак У формируется под влиянием нескольких факторных признаков
Х₁, Х₂, …, Х_р. Уравнение множественной регрессии имеет вид
у = f(х₁, х₂, …, х_р).

Теоретическое линейное уравнение регрессии имеет вид

.

Значение каждого регрессионного коэффициента равно среднему изменению y при увеличении x_j на одну единицу при условии, что все остальные факторы остались неизменными. Для проведения анализа в рамках линейной модели множественной регрессии необходимо выполнение ряда предпосылок МНК, некоторые из них аналогичны парной регрессии:

1⁰. E (ε_i) = 0 (i=1,...,n).

2⁰.

Первая строчка означает гомоскедастичность остатков, вторая предполагает отсутствие автокорреляции.

3⁰. X₁,..., Х_п –неслучайные величины.

4⁰. Модель является линейной относительно параметров.

5⁰. Отсутствие мультиколлинеарности: между объясняющими переменными отсутствует строгая линейная зависимость, что играет важную роль в отборе факторов при решении проблемы спецификации модели.

6⁰. Ошибки имеют нормальное распределение . Выполнимость этого условия нужна для проверки статистических гипотез и построения интервальных оценок.

 

Для нахождения коэффициентов линейной множественной регрессии представим данные наблюдений и параметры модели в матричной форме:

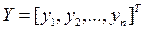– n -мерный транспонированный вектор – столбец наблюдений зависимой переменной;

– (p+1) -мерный транспонированный вектор – столбец параметров уравнения регрессии;

– n -мерный транспонированный вектор – столбец отклонений выборочных значений y_i.

Тогда значения независимых переменных запишем в виде прямоугольной матрицы размерности :

В этих обозначениях эмпирическое уравнение регрессии выглядит так: . Тогда функционал, который минимизируется по МНК, равен: Наилучшей оценкой является вектор .

 

Уравнение регрессии в стандартизованном масштабе имеет вид

,

где ,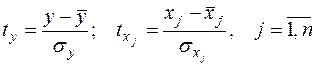

σ -среднее квадратичное отклонение, β_j – стандартизованные коэффициенты регрессии, которые показывают, насколько значений средних квадратичных отклонений (с.к.о.) изменится в среднем результат, если соответствующий фактор х_j изменится на одно с.к.о. при неизменном среднем уровне других факторов.

Применяя МНК, после соответствующих преобразований получим систему нормальных уравнений:

Сравнивая коэффициенты β_j между собой, можно ранжировать факторы по силе их воздействия на результат, а также использовать коэффициенты при отсеве факторов – из модели исключаются факторы с наименьшим значением β_j.

Коэффициенты «чистой» регрессии b_j связаны с
β -коэффициентами формулой .

 

Как и в случае парной регрессии, проверка гипотезы о статистической значимости уравнения регрессии осуществляется на основе дисперсионного анализа: Н₀: D_факт = D_ост против альтернативной гипотезы Н₁: D_факт > D_ост. При этом строится
F -статистика:

.

Если F_наб > F_табл (α; р; n – p – 1), то Н_о отклоняется, т. е. факторная дисперсия превышает остаточную, уравнение регрессии является статистически значимым.

Для проверки общего качества уравнения регрессии используется также коэффициент детерминации R², который рассчитывается аналогично парой регрессии. Анализ статистической значимости коэффициента детерминации проводится на основе проверки Н₀: R² = 0 против альтернативной гипотезы Н₁: R² > 0. Для проверки данной гипотезы используется следующая
F -статистика:

.

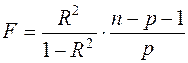Если F_наб > F_табл (α; р; n – p – 1), то Н_о отклоняется, что равносильно статистической значимости R².

Наряду с коэффициентом детерминации используется скорректированный коэффициент детерминации

.

 

Статистическая значимость параметров множественной линейной регрессии с р факторами: Н₀: b_j = 0 проверяется на основе t -статистики:

, ,

где - j -й диагональный элемент обратной матрицы , . Если | t_наб | < t_таб (1 – α; n – p – 1), параметр считается статистически незначимым и Н₀ не может быть отвергнута, фактор х_j линейно не связан с результатом, поэтому переменную х_j рекомендуется исключить из уравнения регрессии.

Доверительные интервалы для значимых коэффициентов находятся по формуле

.

Пусть объясняющие переменные принимают значение
Х^Т₀ = (1; х¹₀; х²₀;…;х^р₀). Тогда доверительный интервал для функции регрессии равен

где .

Доверительный интервал для индивидуальных значений зависимой переменной:

,

где .

 

При исключении или добавлении факторов для проверки статистической значимости оставшихся коэффициентов используют статистику Фишера. Проверяя гипотезу , можно определить, существенно ли ухудшилось качество описания поведения зависимой переменной. Для этого используют статистику

.

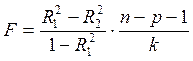Если F_наб > , то Н_о должна быть отклонена. В этом случае одновременное исключение из рассмотрения k объясняющих переменных некорректно.

 

Для оценки тесноты между признаками применяются парные, частные и множественные коэффициенты корреляции и детерминации.

Для линейной регрессии множественный коэффициент корреляции можно определить по формулам:

- , где Δ r – определитель матрицы парных коэффициентов корреляции: ,

а Δr₁₁ – определитель, который остаётся после вычеркивания из матрицы коэффициентов парной корреляции первого столбца и первой строки;

- для модели, в которой присутствуют две независимые переменные, формула упрощается .

Коэффициенты частной корреляции для трехфакторной модели рассчитаем по формулам , , .

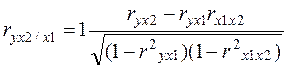Существует тесная связь между коэффициентом частной корреляции и коэффициентом детерминации R²:

.

Рекомендуемая литература [2, с. 4 - 82; 4, с. 154 - 192,
230 - 302; 5, с. 109 - 208, 296 - 327; 6, с. 82-188, 243-254].

 

Пример 2. Исследуется зависимость между стоимостью грузовой автомобильной перевозки Y (тыс. р.), весом груза X₁ (т) и расстоянием Х₂ (тыс. км) по 20 транспортным компаниям. Исходные данные приведены в табл. 6.

Таблица 6

№	Y	X1	X2	№	Y	X1	X2
							1,3
			1,1				0,35
			2,55		5,8		1,65
	7,5		1,7		13,8	3,5	2,9
			2,4		6,2	2,8	0,75
			1,55		7,9		0,6
	11,5		0,6		5,4	3,4	0,9
			2,3				2,5
	15,8		1,4		25,5		2,2
			2,1		7,1	4,5	0,95

Требуется:

1. Построить выборочное уравнение линейной множественной регрессии. Привести полученное уравнение к стандартизированному виду, сделать выводы о влиянии факторов на результирующий фактор. Определить коэффициенты эластичности.

2. Проверить статистическую значимость уравнения регрессии с помощью дисперсионного анализа и через коэффициент детерминации.

3. Проверить статистическую значимость параметров уравнения регрессии и для значимых коэффициентов построить доверительные интервалы.

4. Оцените качество уравнения через среднюю ошибку аппроксимации.

5. Определите парные и частные коэффициенты корреляции, проверить их на значимость. Для значимых коэффициентов постройте доверительные интервалы.

6. Рассчитать частные F -критерии Фишера и оценить целесообразность включения в уравнение одного из факторов после другого.

7. Найти прогнозное значение у_i, если х₁=10, х₂=5, и доверительные интервалы для среднего и индивидуального значения у_{0 .}

Решение

1. Модель специфицируем в виде линейной функции:

.

Вектор В найдем по формуле :

Матрица Х Х^Т

						…
		1,1				…		4,5
…	…	…			1,1	…	2,2	0,95
		2,2
	4,5	0,95

Х^Т*Х (Х^Т*Х)^-1 Х^Т*У

	277,2	31,8		0,344766	-0,00562	-0,13643		454,5
277,2	5860,9	459,235		-0,00562	0,000503	-0,00085		8912,57
31,8	459,235	61,455		-0,13643	-0,00085	0,093251		908,555

В

-17,3133

1,156057

5,10401

Следовательно, уравнение регрессии имеет вид

Y = – 17,31 + 1,16 X₁ + 15,10 Х₂.

Для приведения к стандартному виду построим вспомогательную таблицу (табл. 7).

Таблица 7

№	Y	X1	X2	Y2	X21	X22
			1,1			1,21
			2,55			6,5025
	7,5		1,7	56,25		2,89
			2,4			5,76
			1,55			2,4025
	11,5		0,6	132,25		0,36
			2,3			5,29
	15,8		1,4	249,64		1,96
			2,1			4,41
			1,3			1,69
			0,35			0,1225
	5,8		1,65	33,64		2,7225
	13,8	3,5	2,9	190,44	12,25	8,41
	6,2	2,8	0,75	38,44	7,84	0,5625

Окончание табл.7

№	Y	X1	X2	Y2	X21	X22
	7,9		0,6	62,41		0,36
	5,4	3,4	0,9	29,16	11,56	0,81
			2,5			6,25
	25,5		2,2	650,25		4,84
	7,1	4,5	0,95	50,41	20,25	0,9025
Σ	454,5	277,2	31,8	18206,89	5860,9	61,45

 

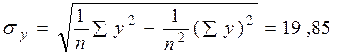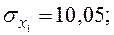
; 0,74;

= 0,77; = 0,56;

t_Y = 0,77t_x1 + 0,56t_x2.

То есть с ростом веса груза на одну сигму при неизменном расстоянии стоимость грузовых автомобильных перевозок увеличивается в среднем на 0,77 сигмы. С ростом расстояния на одну сигму при неизменном весе груза стоимость грузовых автомобильных перевозок увеличивается в среднем на 0,56 сигмы. Поскольку 0,77 > 0,56, то влияние веса груза на стоимость грузовых автомобильных перевозок больше, чем фактора расстояния.

Найдем коэффициенты эластичности:

= ,

= 1,05.

С увеличением среднего веса груза на 1% от его среднего уровня средняя стоимость перевозок возрастет на 0,71% от своего среднего уровня. При увеличении среднего расстояния перевозок на 1% средняя стоимость доставки груза увеличится на 1,05%. Поскольку 0,71 < 1,05, то влияние веса груза на стоимость грузовых автомобильных перевозок меньше, чем фактора расстояния. Различия в силе влияния факторов на результат, полученные при сравнении уравнения регрессии в стандартизованном масштабе и коэффициентов эластичности, объясняются тем, что коэффициент эластичности рассчитывается исходя из соотношения средних, а стандартизованные коэффициенты регрессии - из соотношения средних квадратических отклонений.

 

2. Проверим на значимость уравнение регрессии, для этого составим таблицу (табл. 8).

Таблица 8

№				|(y-yр)/y|
	53,45	799,193	6,00	0,0462095
	17,82	45,293	3,31	0,1123748
	42,04	2628,613	1021,76	0,4322848
	10,64	231,953	9,86	0,4234144
	35,13	105,473	4,537	0,0642756
	44,34	10,693	336,17	0,7018371
	14,91	126,113	11,63	0,2930625
	46,38	856,7329	31,58	0,10909
	18,87	48,025	9,43	0,193736
	16,68	216,973	75,34	1,0896515
	26,64	10,693	0,41	0,0230416
	0,695	279,893	28,143	0,8850491
	11,045	286,625	27,51	0,9097353
	30,5	79,7449	278,89	1,2126453
	-2,777	273,241	80,587	1,4432832
	11,43	219,929	12,461	0,4432973
	0,184	300,329	27,207	0,9609482
	48,24	1106,893	60,218	0,1394274
	26,31	7,673	0,6561	0,0321573
	2,215	244,297	23,863	0,684825
Сум.	454,732	7878,378	2049,568	10,200346

Проверка с помощью дисперсионного анализа:

Н₀: D_факт = D_ост; Н₁: D_факт > D_ост ;

Q_об = 7878,378; Q_ост =2049,558; Q_факт = 5828,82;

F_н = (5828,82/2049,56)·(17/2) = 24,17.

Так как F_н > F_кр(0,05; 2; 17) = 3,59, то нулевая гипотеза отклоняется и уравнение множественной регрессии статистически значимо.

Проверка с помощью коэффициента детерминации:

; .

Он показывает, что 74% различий стоимости всех перевозок объясняется вариацией их грузоподъемности и расстояния, а
16% - другими, неучтенными факторами. Скорректированный коэффициент детерминации достаточно велик, следовательно, смогли учесть в модели наиболее существенные факторы, определяющие стоимость перевозки:

Н₀: R² = 0; Н₁: R² > 0.

.

Так как F_фак > F_кр(0,05; 2; 17) = 3,59, то Н₀ отклоняется, коэффициент детерминации отличается от нуля, следовательно, уравнение регрессии статистически значимо.

 

3. Проверим статистическую значимость коэффициентов регрессии:

Н₀: b₀ = 0; Н₁: b₀ ≠ 0.

; ;

; t_кр(0,95; 17)= 2,11.

Так как t_наб > t_крит, следовательно, коэффициент значимо отличается от нуля, доверительный интервал (– 30,92; – 3,71).

Н₀: b₁ = 0; Н₁: b₁ ≠ 0.

;

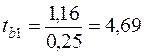; t_кр(0,95; 17)= 2,11.

Так как t_наб > t_крит, следовательно, коэффициент значимо отличается от нуля,доверительный интервал (0,64; 1,68).

Н₀: b₂ = 0; Н₁: b₂ ≠ 0.

;

; t_кр(0,95; 17)= 2,11.

Так как t_наб > t_крит, следовательно, коэффициент значимо отличается от нуля,доверительный интервал (8,03; 22,18).

4.Определим ошибку аппроксимации А = = 51%. Фактические значения стоимости перевозок от расчетных данных по уравнению регрессии в среднем отличаются на 51%.

 

5.Определим парные и частные коэффициенты корреляции. Для этого построим таблицу (табл. 9).

Таблица 9

№	Y	X1	X2	Y2	x12	x22	yx1	yx2	х1x2
			1,1			1,21		17,6	17,6
			2,55			6,5025		188,7	45,9
	7,5		1,7	56,25		2,89		12,75	3,4
			2,4			5,76		79,2	33,6
			1,55			2,4025		40,3	51,15
	11,5		0,6	132,25		0,36		6,9
			2,3			5,29		119,6	57,5
	15,8		1,4	249,64		1,96	205,4	22,12	18,2
			2,1			4,41		16,8	4,2
			1,3			1,69		33,8	27,3
			0,35			0,1225		2,1	3,85
	5,8		1,65	33,64		2,7225	17,4	9,57	4,95
	13,8	3,5	2,9	190,44	12,25	8,41	48,3	40,02	10,15
	6,2	2,8	0,75	38,44	7,84	0,5625	17,36	4,65	2,1
	7,9		0,6	62,41		0,36	134,3	4,74	10,2
	5,4	3,4	0,9	29,16	11,56	0,81	18,36	4,86	3,06
			2,5			6,25
	25,5		2,2	650,25		4,84	229,5	56,1	19,8
	7,1	4,5	0,95	50,41	20,25	0,9025	31,95	6,745	4,275
Ср. знач.	22,73	13,86	1,59	910,34	293,05	3,07	445,63	45,43	22,96

 

.

.

.

Матрица парных коэффициентов корреляции имеет вид .

Проверим их на значимость Н₀: ρ = 0 при Н₁: ρ ≠ 0

> t_кр(0,05; 18) = 2,1 -гипотеза Н₀ отвергается, коэффициент корреляции статистически значим;

> t_кр(0,05; 18) = 2,1 -гипотеза Н₀ отвергается, коэффициент корреляции статистически значим;

< t_кр(0,05; 18) = 2,1 -гипотеза Н₀ не отвергается, коэффициент корреляции статистически не значим.

На основе матрицы корреляции найдем еще раз коэффициент детерминации: Δ = 0,256; Δ₁₁ = 0,984; R² = 1 – 0,246/0,984 =
= 0,74; . Величина множественного коэффициента детерминации свидетельствует о сильной взаимосвязи стоимости перевозки с весом груза и расстоянием, на которое он перевозится. Множественный коэффициент детерминации можно рассчитать по формулам

,

или .

Рассчитаем частные коэффициенты корреляции. Коэффициенты частной корреляции характеризуют тесноту связи между двумя переменными, исключив влияние третьей переменной:

;

;

.

Связь между стоимостью перевозок и весом груза прямая и тесная, между стоимостью перевозок и расстоянием прямая и тесная, между весом груза и расстоянием обратная и средняя. Проверим их на значимость Н₀: ρ = 0 при Н₁: ρ ≠ 0

> t_кр(0,05; 18) = 2,1 -гипотеза Н₀ отвергается, коэффициент корреляции статистически значим;

> t_кр(0,05; 18) = 2,1 -гипотеза Н₀ отвергается, коэффициент корреляции статистически значим;

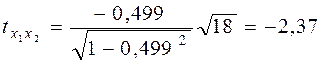> t_кр(0,05; 18) = 2,1 -гипотеза Н₀ отвергается, коэффициент корреляции статистически значим.

Для значимых коэффициентов корреляции построим доверительный интервал. Для этого вычислим ; ; ; ; .

Тогда ;

;

.

 

6. Рассчитаем частные F -критерии Фишера и оценим целесообразность включения в уравнение одного из факторов после другого:

Н₀: R² = r²_yx1; Н₁: R² ≠ r²_yx1.

F_часх1= > F_кр = 4,45, следовательно, приходим к выводу о целесообразности включения в модель фактора х₂ после фактора х₁.

Н₀: R² = r²_yx2; Н₁: R² ≠ r²_yx2.

F_часх2= 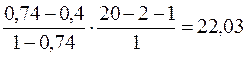> F_кр = 4,45, следовательно, приходим к выводу о нецелесообразности включения в модель фактора х₁ после фактора х₂.

 

7. Стоимость грузовых перевозок при весе груза 10 т и расстояние 5 км, т.е. x₀^T=(1; 10; 5), составит y₀ = – 17,31 + 1,16 10 +
+ 15,10 5 = 69,77 тыс. р.

Доверительный интервал для среднего составит
(44,77; 94,76), где Х₀^Т·(Х^Т·Х)^-1·Х_о = 1,16; ; t_кр(0,95; 17) = 2,11.

Доверительный интервал для индивидуального значения ― (35,69; 103,85), где .

Вопросы для самоконтроля

1. Перечислите предпосылки МНК. Каковы последствия их невыполнимости либо выполнимости? В чем суть наилучших линейных несмещенных оценок?

2. Сформулируйте алгоритм определения коэффициентов регрессии в матричной форме. Что характеризуют коэффициенты регрессии?

3. Опишите схему проверки гипотез о величинах коэффициентов регрессии. В чем суть статистической значимости коэффициентов регрессии? Опишите «грубое» правило анализа статистической значимости коэффициентов регрессии.

4. Как определяются стандартные ошибки регрессии и коэффициентов регрессии? Приведите схему определения интервальных оценок коэффициентов регрессии.

5. Как осуществляется анализ качества эмпирического уравнения множественной линейной регрессии?

6. Объясните суть коэффициента детерминации множественной регрессии. В каких пределах он изменяется? Сформулируйте схему проверки статистической значимости коэффициента детерминации.

7. Чем скорректированный коэффициент детерминации отличается от обычного?

8. Как строится и что позволяет определить доверительный интервал для условного математического ожидания зависимой переменной? В чем суть предсказания индивидуальных значений зависимой переменной?

9. Сформулируйте критерий проверки целесообразности включения или исключения независимых факторов.

10. Что называется линейным коэффициентом множественной корреляции и как с помощью матрицы парных коэффициентов корреляции его можно определить?

11. Как определяются частные коэффициенты корреляции? Как связаны коэффициент частной корреляции и коэффициент детерминации?

12. Что представляет собой фиктивная переменная? Каковы основные причины использования фиктивных переменных в регрессионных моделях? В чем суть «ловушки» фиктивных переменных?

13. Что представляют собой ANOVA-модели? Что представляют собой ANCOVA-модели? Приведите примеры их использования.

14. Объясните значение термина «мультиколлинеарность». В чем отличие совершенной и несовершенной мультиколлинеарности? Каковы последствия мультиколлинеарности?

15. Как можно обнаружить и устранить мультиколлинеарность?

16. В чем сущность гетероскедастичности? Сформулируйте последствия гетероскедастичности.

17. Приведите схемы теста ранговой корреляции Спирмена и Голдфелда – Квандта для проверки на гомоскедастичность.

18. В чем суть метода взвешенных наименьших квадратов?

19. Что такое автокорреляция? Каковы причины и последствия автокорреляции?

20. Опишите схему использования статистики Дарбина – Уотсона. Перечислите ограничения ее использования.

21. Опишите авторегрессионую схему первого порядка AR(1).

 

Временные ряды

Экономические процессы и явления, их связи и зависимости могут рассматриваться как в пространстве, так и во времени, путем построения и анализа одного или нескольких временных рядов.

Временной ряд (динамический ряд или ряд динамики) ― совокупность изучаемого показателя в последовательные моменты времени. Отдельные наблюдения называются уровнями ряда у_t, t=1,…,n, где n – число уровней. Под длиной ряда понимают время, прошедшее от начального момента наблюдения до конечного. Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые можно условно разделить на три группы:

- факторы, формирующие тенденцию ряда (Т). Тенденция характеризует долговременное воздействие факторов на динамику показателя. Тенденция может быть возрастающей или убывающей;

- факторы, формирующие циклические колебания ряда (S). Циклические колебания могут носить сезонный характер или отражать динамику конъюнктуры рынка, а также фазу бизнес-цикла, в которой находится экономика страны;

- случайные факторы (E), отражающие влияние, не поддающееся учету и регистрации.

Модель, в которой временной ряд представлен как сумма перечисленных выше компонент, называется аддитивной моделью временного ряда (), в случае произведения – мультипликативной моделью ().

Основная задача эконометрического исследования временного ряда – выявление количественного выражения каждой из компонент и использование полученной информации для прогноза будущих значений ряда или построение модели взаимосвязи двух или более временных рядов.

Для выявления наличия той или иной неслучайной компоненты исследуется корреляционная зависимость между последовательными уровнями временного ряда, или автокорреляция уровней ряда. Количественно автокорреляцию можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени. Коэффициент автокорреляции уровней ряда первого порядка измеряет зависимость между соседними уровнями ряда t и t-1 и вычисляется по формуле

где

Аналогично определяются коэффициенты автокорреляции более высоких порядков. Так, коэффициент автокорреляции порядка характеризует тесноту связи между уровнями и и определяется по формуле

где

Число периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом. Последовательность коэффициентов автокорреляции уровней различных порядков, начиная с первого, называется автокорреляционной функцией временного ряда. График зависимости ее значений от величины лага называется коррелограммой.

Если наиболее высоким является коэффициент автокорреляции первого порядка, очевидно, исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка τ, ряд содержит циклические колебания с периодичностью в τ моментов времени. Если ни один из коэффициентов автокорреляции не является значимым, то либо ряд не содержит тенденции и циклических колебаний и имеет только случайную составляющую, либо ряд содержит сильную нелинейную тенденцию, для исследования которой нужно провести дополнительный анализ.

В случае, если при анализе структуры временного ряда обнаружена только тенденция и отсутствуют циклические колебания, следует приступать к моделированию тенденции. Если же во временном ряде имеют место и циклические колебания, прежде всего следует исключить именно циклическую составляющую и лишь затем приступать к моделированию тенденции.

Построение аналитической функции для моделирования тенденции (тренда) временного ряда называют аналитическим выравниванием временного ряда. Тенденция во времени может принимать разные формы, для ее формализации используются следующие функции:

- линейная: ;

- полиномиальная: , где
а₁ - линейный прирост, а₂ - ускорение роста, а₃ - изменение ускорения роста;

- гипербола: ;

- экспоненциальный тренд: (или ), где а - начальный уровень, e^b - средний за единицу времени коэффициент роста;

- степенной тренд: .

Параметры каждого из трендов можно определить обычным МНК, используя в качестве независимой переменной время t, а в качестве зависимой переменной – фактические уровни временного ряда y_t. Для нелинейных трендов предварительно проводят стандартную процедуру линеаризации.

Для выявления полиномиального тренда применяется метод последовательных разностей, состоящий в вычислении последовательных разностей Δt_к при к = 1, 2,…,n:

Δt = y_t - y_t-1; Δt₂ = Δ_t - Δ_t-1;…; Δt_к = Δt_(к-1) – Δ(t-1)_(к-1).

Если примерно одинаковы все абсолютные приросты Δt, то имеем линейный тренд; если абсолютные ускорения Δt₂, то тренд - парабола. Анализ цепных коэффициентов роста К_t = y_t /y_t-1 позволяет выявить наличие экспоненциального или степенного тренда.

Рекомендуемая литература [4, с. 310 - 342; 5, с. 290 - 330; 6,
с. 133 - 149, 202 - 222].

 

Пример 3. Пусть имеются данные (табл. 10) об объёмах потребления электроэнергии жителями района за 16 кварталов, м. квт.-ч:

Таблица 10

t	yt	t	yt
	4,4		5,6
			6,4
	7,2
	4,8		6,6
			10,8

Требуется:

1. Построить график временного ряда и определить автокорреляционную функцию. Определить составляющие временного ряда.

2. Если ряд содержит сезонную компоненту, то выявить и устранить ее с помощью статистических методов, построив аддитивную модель.

3. Если ряд содержит тенденцию, то построить уравнение тренда.

Решение

1. Нанесем исходные значения на график (рис. 3). Рассчитаем коэффициент автокорреляции первого порядка. Для этого определим средние значения:

С учетом этих значений можно построить вспомогательную таблицу (табл. 11).

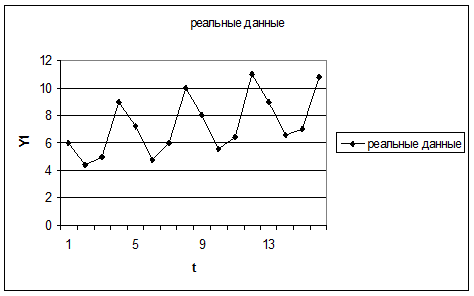
Рис. 3. Динамика объема потребления

 

Таблица 11

t	y t