При однофакторном анализе изучается влияние определяющего фактора X на изменение результативного признака Y. Уравнение связи между двумя переменными имеет вид Y = f(X), где
Y - зависимая переменная (результативный признак); X - независимая переменная (факторный признак).
Уравнения регрессии подразделяются на линейные и нелинейные.
Модель линейной регрессии имеет вид Уi = α + βXi + εi,
(i = 1,…,n), где ε - случайный член, характеризующий отклонение фактических значений результативного признака от значений, найденных по уравнению регрессии. При этом на случайный член накладываются ограничения называемые условиями Гаусса-Маркова:
1. E (εi) = 0, i=1,...,n.
 Иногда случайный член будет положительным, иногда отрицательным, но он не должен иметь систематического смещения ни в одном из двух возможных направлений.
Иногда случайный член будет положительным, иногда отрицательным, но он не должен иметь систематического смещения ни в одном из двух возможных направлений.
2. 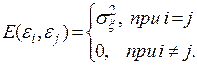
Первое условие означает требование постоянства дисперсии регрессионных остатков, которое называют гомоскедастичностью остатков.
Второе условие предполагает отсутствие систематической связи между значениями случайного члена в любых двух наблюдениях, это условие называется автокорреляцией.
3. X1,..., Хп - неслучайные величины.
Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК): среди всех возможных значений α и β следует выбрать такую пару  , для которых сумма квадратов отклонений фактических значений
, для которых сумма квадратов отклонений фактических значений  от теоретических
от теоретических  минимальна:
минимальна: 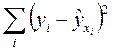 → min.
→ min.
Нелинейные регрессии подразделяются:
1) на регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемому параметру. Например, полиномы 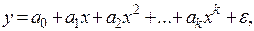 равносторонняя гипербола
равносторонняя гипербола  . Для линейной по параметру регрессии оценки параметров определяются обычным МНК, предварительно заменяется нелинейная переменная;
. Для линейной по параметру регрессии оценки параметров определяются обычным МНК, предварительно заменяется нелинейная переменная;
2) регрессии, нелинейные по оцениваемому параметру. Например, степенная y = a·xb·ε, показательная y = a·bx·ε, экспоненциальная y = ea+bx·ε. Данный класс моделей подразделяется на внутренне линейные и внутренне нелинейные модели:
- нелинейная модель внутренне линейна, если с помощью соответствующих преобразований может быть приведена к линейному виду;
- нелинейная модель внутренне нелинейная, если не может быть сведена к линейной.
Рекомендуемая литература [1, с. 3 - 9, 65 - 75; 4, с. 98 - 147,
200 - 222; 5, с. 34 - 88, 62 - 88; 6, с. 50 - 80, 124 - 130].
Пример 1. Имеются выборочные данные о стоимости квартир и общей площади в г. Краснодаре, май 2004 г.
Таблица 2
| Рыночная стоимость квартиры, тыс. у.е. (У)
| Общая площадь квартиры, м2 (Х)
| Рыночная стоимость квартиры, тыс. у.е. (У)
| Общая площадь квартиры, м2 (Х)
|
| 13,8
|
|
|
|
| 13,8
|
| 21,5
|
|
|
|
|
|
|
| 22,5
|
|
|
|
|
|
|
|
|
|
|
| 37,9
|
|
|
|
| 27,5
|
|
| 20,9
|
| ―
| ―
|
Требуется:
1. Построить выборочное уравнение парной линейной регрессии. Найти коэффициент эластичности.
2. На уровне значимости α = 0,05 оценить значимость уравнения и коэффициентов регрессии. Для значимых коэффициентов регрессии построить доверительные интервалы.
3. Оценить качество уравнения с помощью средней ошибки аппроксимации.
4. Оценить тесноту связи между переменными с помощью выборочного коэффициента корреляции, построить доверительный интервал.
5. Построить графики зависимостей уi и  от х, а также доверительный интервал для значений уi.
от х, а также доверительный интервал для значений уi.
6. Определить прогнозное значение результативного признака, если возможное значение факторного признака составит 1,2 от его среднего уровня по совокупности. Найти доверительные интервалы для прогнозного значения.
7. Построить уравнения регрессий:  ,
,  ,
,  и
и  , сделать вывод по наилучшей модели
, сделать вывод по наилучшей модели
Решение
1. Для проведения всех расчетов строим вспомогательную таблицу (табл. 3).
Таблица 3
| № п/п
| X
| Y
| х2
| y2
| ху
| 
| (У -  )2 )2
| (У -  )2 )2
|
|
|
| 13,8
|
| 190,44
|
| 14,734
| 97,204
| 116,50
|
|
|
| 13,8
|
| 190,44
|
| 16,847
| 60,009
| 116,50
|
|
|
|
|
| 196,00
|
| 15,640
| 80,170
| 112,22
|
|
|
| 22,5
|
| 506,25
|
| 22,883
| 2,925
| 4,38
|
|
|
|
|
| 576,00
|
| 21,374
| 10,364
| 0,35
|
|
|
|
|
| 784,00
|
| 28,919
| 18,714
| 11,61
|
|
|
|
|
| 1024,00
|
| 33,447
| 78,379
| 54,86
|
|
|
| 20,9
|
| 436,81
|
| 25,901
| 1,710
| 13,64
|
|
|
|
|
| 484,00
|
| 19,261
| 28,430
| 6,73
|
| № п/п
| X
| Y
| х2
| y2
| ху
| 
| (У -  )2 )2
| (У -  )2 )2
|
|
|
| 21,5
|
| 462,25
|
| 20,770
| 14,615
| 9,57
|
|
|
|
|
| 1024,00
|
| 33,447
| 78,379
| 54,86
|
|
|
|
|
| 1225,00
|
| 27,410
| 7,935
| 108,30
|
|
|
|
|
| 576,00
|
| 23,788
| 0,648
| 0,35
|
|
|
| 37,9
|
| 1436,41
|
| 38,577
| 195,552
| 177,07
|
|
|
| 27,5
|
| 756,25
|
| 25,901
| 1,710
| 8,45
|
| ∑
|
| 368,9
|
| 9867,85
|
| 368,9
| 676,744
| 795,37
|
| Ср. знач.
| 65,667
| 24,593
| 4807,4
| 657,857
| 1764,447
| 24,593
| ―
| ―
|
| № п/п
| 
| (Х -  )2 )2
| 
| № п/п
| 
| (Х -  )2 )2
| 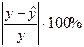
|
|
| 0,873
| 6,769
| 6,769
|
| 7,500
| 312,1111
| 12,449
|
|
| 9,283
| 22,078
| 22,078
|
| 0,532
| 160,4444
| 3,394
|
|
| 2,688
| 11,711
| 11,711
|
| 2,092
| 860,4444
| 4,520
|
|
| 0,147
| 1,702
| 1,702
|
| 57,604
| 87,11111
| 21,685
|
|
| 6,896
| 10,942
| 10,942
|
| 0,045
| 7,111111
| 0,881
|
|
| 0,845
| 3,283
| 3,283
|
| 0,459
| 2146,778
| 1,787
|
|
| 2,092
| 4,520
| 4,520
|
| 2,556
| 18,77778
| 5,814
|
|
| 25,012
| 12,449
| 23,929
| ∑
| 118,625
| 7429,33
| 135,465
|
Используя метод наименьших квадратов, найдем значения коэффициентов регрессии:

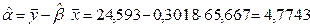 .
.
Таким образом, уравнение регрессии имеет вид
 .
.
Коэффициент регрессии показывает, что при увеличении общей площади квартиры на 1 м2 стоимость в среднем увеличивается на 301,8 у.е.
Коэффициент эластичности равен  = 0,806. Он показывает, что при увеличении общей площади квартиры на 1 % стоимость в среднем возрастает на 0,81%.
= 0,806. Он показывает, что при увеличении общей площади квартиры на 1 % стоимость в среднем возрастает на 0,81%.
Заметим, что  = 0, что согласуется с первым ограничением модели парной регрессии.
= 0, что согласуется с первым ограничением модели парной регрессии.
2. Проведем проверку качества уравнения с помощью дисперсионного анализа и коэффициента детерминации.
Сопоставляя факторную и остаточную дисперсии  ,
,  , получим F -критерий для проверки нулевой гипотезы о существенности статистической связи между у и х
, получим F -критерий для проверки нулевой гипотезы о существенности статистической связи между у и х
 .
.
Так как Fфак > Fтаб (0,05;1;13) = 4,67, то Н0 отклоняется и Dфакт существенно превышает Dост, т.е. статистическая связь между y и x существует.
Для проверки гипотезы  ,
,  рассчитаем коэффициент детерминации
рассчитаем коэффициент детерминации
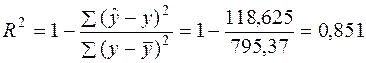 .
.
Он показывает, что 85,1% различий в стоимости квартир объясняется вариацией их общей площади, а 14,9% - другими, неучтенными факторами (местоположение квартир, благоустроенность территории и др.). Используя F -критерий, получим  . Так как Fфак > Fтаб, то Н0 отклоняется, коэффициент детерминации отличается от нуля, следовательно, уравнение регрессии статистически значимо.
. Так как Fфак > Fтаб, то Н0 отклоняется, коэффициент детерминации отличается от нуля, следовательно, уравнение регрессии статистически значимо.
Статистическая значимость коэффициента регрессии
Н0: β = 0 при Н1: β ≠ 0 проводится с использованием критерия
t -Стьюдента

где s2 =  ― остаточная дисперсия.
― остаточная дисперсия.
Так как |tнаб| > tкр(0,05; 13) = 2,16, то гипотеза Н0 отвергается, коэффициент статистически значим, таким образом подтверждается вывод о значимости влияния общей площади на стоимость квартир.
Н0: a = 0 Н1: a ≠ 0 проверим по формуле
 ,
,
где sа =  - остаточная дисперсия. Так как
- остаточная дисперсия. Так как
|tнаб| < tкр(0,05; 13) = 2,16, то гипотеза Н0 не отвергается, коэффициент статистически не значим.
Для значимого коэффициента регрессии найдем доверительный интервал по формуле  .
.
0,302 ± 2,16·0,035, т.е. при увеличении общей площади квартиры на 1 м2 стоимость в среднем увеличивается от 226,1 до 377,5 у.е.
3. Коэффициент аппроксимации равен
 .
.
Фактические значения стоимости квартир от расчетных данных по уравнению регрессии в среднем различаются на 9%. Качество уравнения считается хорошим, если ошибка аппроксимации не превышает 8 - 10%. Полученное уравнение можно оценить как вполне хорошее.
4. При линейной зависимости теснота связи между переменными Х и У определяется с помощью коэффициента корреляции:

 .
.
Так как значение коэффициента корреляции близко к единице, то между признаками связь очень тесная, прямая, близкая к линейной зависимости. Заметим, что для линейного коэффициента корреляции r2 = R2.
Для проверки гипотезы Н0: ρ = 0 при Н1: ρ ≠ 0 применим критерий t- Стьюдента
 .
.
Так как |tнаб| < tкр(0,05; 13) = 2,16, то гипотеза Н0 отвергается, коэффициент корреляции статистически значим. При парной линейной зависимости оценка значимости всего уравнения и регрессии дает одинаковые результаты, так как t2b = t2r = F.
Для значимого коэффициента корреляции построим доверительный интервал, который с заданной надежность γ содержит неизвестный генеральный коэффициент ρ. Построим сначала доверительный интервал для Е(z):
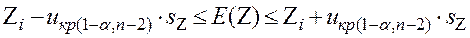 ,
,
где 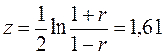 - распределение Фишера,
- распределение Фишера,
 ,
,  - нормированное отклонение, определяется с помощью функции Лапласа Ф(uкр) = 1 - α.
- нормированное отклонение, определяется с помощью функции Лапласа Ф(uкр) = 1 - α.
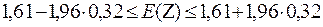 →
→  .
.
Используя обратное преобразование Фишера, получим доверительный интервал для коэффициента корреляции:
0,755 ≤ ρ ≤ 0,977.
5. Построим графики зависимостей уi и  от х, а также доверительные интервалы для значений
от х, а также доверительные интервалы для значений  . Рассчитаем для каждого значения хi минимальные и максимальные значения
. Рассчитаем для каждого значения хi минимальные и максимальные значения  по формулам
по формулам
 ,
,  .
.
Получим вспомогательную таблицу (табл. 4).
Таблица 4
| X
| Y
| 
| Sy
| Ymin
| Ymax
|
|
| 13,8
| 14,734
| 1,38528
| 11,74192
| 17,7263249
|
|
| 14,0
| 15,640
| 1,299738
| 12,83212
| 18,446993
|
|
| 13,8
| 16,847
| 1,190575
| 14,27517
| 19,4184514
|
Окончание табл.4
| X
| Y
| 
| Sy
| Ymin
| Ymax
|
|
| 22,0
| 19,261
| 0,995831
| 17,11031
| 21,4123056
|
|
| 21,5
| 20,770
| 0,897439
| 18,8319
| 22,7088418
|
|
| 24,0
| 21,374
| 0,864916
| 19,50578
| 23,2422165
|
|
| 22,5
| 22,883
| 0,804843
| 21,1446
| 24,6215237
|
|
| 24,0
| 23,788
| 0,785536
| 22,09174
| 25,4852578
|
|
| 20,9
| 25,901
| 0,794605
| 24,18484
| 27,6175341
|
|
| 27,5
| 25,901
| 0,794605
| 24,18484
| 27,6175341
|
|
| 35,0
| 27,410
| 0,84577
| 25,58339
| 29,2371135
|
|
| 28,0
| 28,919
| 0,927722
| 26,91544
| 30,9231935
|
|
| 32,0
| 33,447
| 1,290412
| 30,65921
| 36,2337946
|
|
| 32,0
| 33,447
| 1,290412
| 30,65921
| 36,2337946
|
|
| 37,9
| 38,577
| 1,801413
| 34,68627
| 42,4683705
|

Рис. 1. Линейная зависимость
6. Прогнозное значение результативного признака определяется путем подстановки в уравнение регрессии прогнозного или возможного значения факторного признака. По условию  . Тогда прогнозное значение стоимости квартиры составит
. Тогда прогнозное значение стоимости квартиры составит  = 28,56. Значит, при общей площади квартиры в 78,8 м2 возможная ее стоимость составит 28,56 тыс. у.е.
= 28,56. Значит, при общей площади квартиры в 78,8 м2 возможная ее стоимость составит 28,56 тыс. у.е.
При этом доверительные интервалы, найденные по формулам  ,
,
 , составят
, составят  . При общей площади квартиры в 78,8 м2 ее стоимость составит от 26,6 тыс. у.е. до 30,5 тыс. у.е.
. При общей площади квартиры в 78,8 м2 ее стоимость составит от 26,6 тыс. у.е. до 30,5 тыс. у.е.
7. Предположим, что связь между признаками носит нелинейный характер y = a·хb·ε. Для нахождения параметров регрессии проведем линеаризацию: lny = lna +blnx + lnε. После замены A = lna, Y* = lny, Х* = lnх, Е* = lnε получим линейное уравнение
Y* = A + bХ* + E*. Составляем вспомогательную табл. 5 для преобразованных данных:
Таблица 5
| n
| X*
| Y*
| X*2
| X* Y*
| 
| ε2
| ( )2 )2
|
|
| 3,497
| 2,625
| 12,226
| 9,177
| 13,783
| 0,000
| 116,496
|
|
| 3,689
| 2,625
| 13,608
| 9,682
| 16,217
| 5,844
| 116,496
|
|
| 3,584
| 2,639
| 12,842
| 9,457
| 14,835
| 0,697
| 112,219
|
|
| 4,094
| 3,114
| 16,764
| 12,748
| 22,849
| 0,122
| 4,382
|
|
| 4,007
| 3,178
| 16,059
| 12,736
| 21,228
| 7,681
| 0,352
|
|
| 4,382
| 3,332
| 19,202
| 14,602
| 29,141
| 1,303
| 11,605
|
|
| 4,554
| 3,466
| 20,738
| 15,783
| 33,699
| 2,886
| 54,859
|
|
| 4,248
| 3,040
| 18,050
| 12,914
| 26,030
| 26,318
| 13,641
|
|
| 3,871
| 3,091
| 14,986
| 11,966
| 18,920
| 9,484
| 6,725
|
|
| 3,970
| 3,068
| 15,763
| 12,181
| 20,574
| 0,858
| 9,569
|
|
| 4,554
| 3,466
| 20,738
| 15,783
| 33,699
| 2,886
| 54,859
|
|
| 4,317
| 3,555
| 18,641
| 15,350
| 27,594
| 54,853
| 108,299
|
|
| 4,143
| 3,178
| 17,166
| 13,167
| 23,811
| 0,036
| 0,352
|
|
| 4,718
| 3,635
| 22,264
| 17,152
| 38,732
| 0,692
| 177,067
|
|
| 4,248
| 3,314
| 18,050
| 14,080
| 26,030
| 2,161
| 8,449
|
| Σ.
| 61,878
| 47,325
| 257,094
| 196,777
| 367,143
| 115,819
| 795,369
|
| Ср. знач.
| 4,125
| 3,155
| 17,140
| 13,118
| 24,476
| ―
| ―
|
b = 0,846, A = - 2,333. После потенцирования а = е-0,333 = 0,717 находим искомое уравнение регрессии: У=0,717х 0,846. Индекс корреляции ρху = 0,924, индекс детерминации R2 = 0,854, который показывает, что 85,4% вариации результативного признака объясняется вариацией признака-фактора, а 14,6% приходится на долю прочих факторов. Средняя ошибка аппроксимации
А = 8,25% показывает, что линия регрессии хорошо приближает исходные данные.
F -критерий Фишера: Fн = 76,275 >Fкр(0,05; 1; 13) = 4,67, следовательно, уравнение статистически значимо. Изобразим на рис. 2 исходные данные и линию регрессии:

Рис. 2. График степенной функции
Сравним построенные модели:
| Модель
| Индекс детерминации, R2
|  , % , %
|
 = a +b·x = a +b·x
| 0,851
| 9,03%
|
 = a·xb = a·xb
| 0,854
| 8,25%
|
Наиболее хорошо исходные данные аппроксимирует степенная модель, так как она имеет максимальный коэффициент детерминации и минимальную ошибку аппроксимации.
Индекс детерминации R2 можно сравнивать с коэффициентом детерминации r2 для обоснования возможности применения линейной функции. Практически, если величина (R2 - r2) не превышает 0,01, то линейная зависимость считается оправданной. Поэтому наилучшей итоговой моделью считаем линейную.
Вопросы для самоконтроля
1. Сформулируйте основные этапы прикладного эконометрического исследования.
2. Классифицируйте основные методы и модели эконометрики.
3. Какие типы данных существуют?
4. Что такое функция регрессии? Назовите основные причины наличия в регрессионной модели случайного отклонения.
5. Сформулируйте модель парной регрессии. Перечислите основные предположения эконометрического моделирования.
6. В чем состоит суть метода наименьших квадратов?
7. Опишите алгоритм нахождения коэффициентов парной линейной регрессии. Как интерпретируются эти коэффициенты?
8. Каким образом находится коэффициент корреляции парной регрессии и какова его связь с коэффициентом регрессии? Как строится доверительный интервал для коэффициента корреляции?
9. Сформулируйте свойства коэффициента корреляции.
10. Как осуществляется анализ статистической значимости уравнения регрессии?
11. Объясните суть коэффициента детерминации 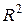 . В каких пределах он изменяется? Как связаны между собой коэффициенты корреляции и детерминации?
. В каких пределах он изменяется? Как связаны между собой коэффициенты корреляции и детерминации?
12. Опишите схему проверки статистической значимости коэффициентов регрессии. Приведите формулы нахождения интервальных оценок коэффициентов регрессии.
13. Как строится и что позволяет определить доверительный интервал для условного математического ожидания зависимой переменной? В чем суть предсказания индивидуальных значений зависимой переменной?
14. Сформулируйте основные формулы для нахождения коэффициента регрессии линейного уравнения без свободного члена.
15. Как классифицируются нелинейные модели регрессии? Приведите примеры использования логарифмических, обратных и степенных моделей.
16. В чем состоит принцип линеаризации нелинейной модели? Изменяются ли свойства случайного отклонения при преобразовании уравнения регрессии?
17. Опишите схему проверки значимости нелинейного уравнения регрессии.
18. Как определяется коэффициент аппроксимации?
19. Какой принцип выбора существует между линейной и нелинейными моделями?



 Иногда случайный член будет положительным, иногда отрицательным, но он не должен иметь систематического смещения ни в одном из двух возможных направлений.
Иногда случайный член будет положительным, иногда отрицательным, но он не должен иметь систематического смещения ни в одном из двух возможных направлений.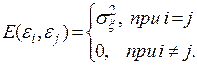
 , для которых сумма квадратов отклонений фактических значений
, для которых сумма квадратов отклонений фактических значений  от теоретических
от теоретических  минимальна:
минимальна: 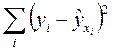 → min.
→ min.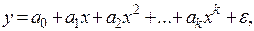 равносторонняя гипербола
равносторонняя гипербола  . Для линейной по параметру регрессии оценки параметров определяются обычным МНК, предварительно заменяется нелинейная переменная;
. Для линейной по параметру регрессии оценки параметров определяются обычным МНК, предварительно заменяется нелинейная переменная; от х, а также доверительный интервал для значений уi.
от х, а также доверительный интервал для значений уi. ,
,  ,
,  и
и  , сделать вывод по наилучшей модели
, сделать вывод по наилучшей модели
 )2
)2

 )2
)2
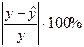

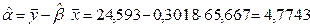 .
. .
. = 0,806. Он показывает, что при увеличении общей площади квартиры на 1 % стоимость в среднем возрастает на 0,81%.
= 0,806. Он показывает, что при увеличении общей площади квартиры на 1 % стоимость в среднем возрастает на 0,81%. = 0, что согласуется с первым ограничением модели парной регрессии.
= 0, что согласуется с первым ограничением модели парной регрессии. ,
,  , получим F -критерий для проверки нулевой гипотезы о существенности статистической связи между у и х
, получим F -критерий для проверки нулевой гипотезы о существенности статистической связи между у и х .
. ,
,  рассчитаем коэффициент детерминации
рассчитаем коэффициент детерминации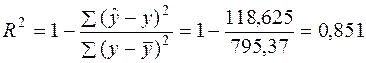 .
. . Так как Fфак > Fтаб, то Н0 отклоняется, коэффициент детерминации отличается от нуля, следовательно, уравнение регрессии статистически значимо.
. Так как Fфак > Fтаб, то Н0 отклоняется, коэффициент детерминации отличается от нуля, следовательно, уравнение регрессии статистически значимо.
 ― остаточная дисперсия.
― остаточная дисперсия. ,
, - остаточная дисперсия. Так как
- остаточная дисперсия. Так как  .
. .
.
 .
. .
.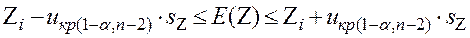 ,
,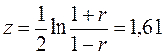 - распределение Фишера,
- распределение Фишера, ,
,  - нормированное отклонение, определяется с помощью функции Лапласа Ф(uкр) = 1 - α.
- нормированное отклонение, определяется с помощью функции Лапласа Ф(uкр) = 1 - α.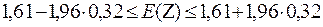 →
→  .
. от х, а также доверительные интервалы для значений
от х, а также доверительные интервалы для значений  ,
,  .
.
 . Тогда прогнозное значение стоимости квартиры составит
. Тогда прогнозное значение стоимости квартиры составит  = 28,56. Значит, при общей площади квартиры в 78,8 м2 возможная ее стоимость составит 28,56 тыс. у.е.
= 28,56. Значит, при общей площади квартиры в 78,8 м2 возможная ее стоимость составит 28,56 тыс. у.е. ,
, , составят
, составят  . При общей площади квартиры в 78,8 м2 ее стоимость составит от 26,6 тыс. у.е. до 30,5 тыс. у.е.
. При общей площади квартиры в 78,8 м2 ее стоимость составит от 26,6 тыс. у.е. до 30,5 тыс. у.е.
 )2
)2

 , %
, %
 = a +b·x
= a +b·x
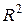 . В каких пределах он изменяется? Как связаны между собой коэффициенты корреляции и детерминации?
. В каких пределах он изменяется? Как связаны между собой коэффициенты корреляции и детерминации?

