На основании полученных в табл. 4.7 данных об индексах сезонности построен график сезонной волны (рис.4.3), который наглядно демонстрирует наличие сезонной компоненты в реализации продукции
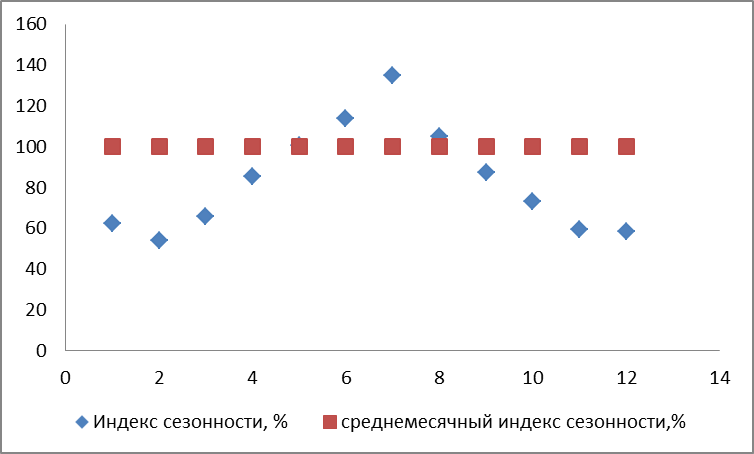
Рис.4.3. Сезонная волна динамики объемов реализации за пятилетний период
Вывод. В динамике объемов реализации продукции явно прослеживается наличие сезонной компоненты. Наибольшим средним значением объемов реализации продукции за пять лет характеризуется месяц июль – 3372.6 тыс. тонн (ISиюль =161.4%), а наименьшее среднее значение приходится на февраль – 1369.2 тыс. тонн (Isфевраль= 65.5%).
3. Расчет прогнозных оценок помесячной реализации продукции на 6-ой год при необходимости увеличить годовую реализацию продукции до 36 000+ 3N тонн (N=204).
3.1. Из формулы индекса сезонности ISi=  *100% следует формула прогнозной оценки на i-ый месяц:
*100% следует формула прогнозной оценки на i-ый месяц:
𝑦̅𝑖= 
𝑦̅ - прогнозируемая среднемесячная реализация.
3.2. Расчет y:
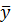 = 36612 / 12 = 3 051 тыс. тонн
= 36612 / 12 = 3 051 тыс. тонн
3.3. Расчет помесячных прогнозных оценок 𝑦̅𝑖=  путем подстановки значения
путем подстановки значения 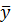 =3051 и помесячных индексов 𝐼𝑠𝑖, рассчитанных в последнем столбце табл.4.7.
=3051 и помесячных индексов 𝐼𝑠𝑖, рассчитанных в последнем столбце табл.4.7.
Таблица 4.8
| Месяцы
| Индекс сезонности
%
ISi
| Прогнозные оценки помесячной реализации продукции на 6-ой год, тыс. тонн
𝑦̅𝑖
|
| Январь
| 75.4
| 2300.5
|
| Февраль
| 65.5
| 1998.4
|
| Март
| 79.1
| 2413.3
|
| Апрель
| 102.6
| 3130.3
|
| Май
| 120.2
| 3667.3
|
| Июнь
| 135.6
| 4137.2
|
| Июль
| 161.4
| 4924.3
|
| Август
| 125.2
| 3819.9
|
| Сентябрь
| 104.5
| 3188.3
|
| Октябрь
| 87.9
| 2681.8
|
| Ноябрь
| 71.7
| 2187.6
|
| Декабрь
| 70.8
| 2160.1
|
| Итого
| -
|
|
Задача 5.1
Имеются данные о продаже условного товара "А" в магазинах города в третьем и четвертом кварталах (табл.5.1).
Таблица 5.1
Исходные данные
| Форма торговли
| Объем продаж, тыс.кг
| Цена за 1 кг
|
| III квартал
| IV квартал
| III квартал
| IV квартал
|
| Сетевая
| 85.6
| 66.2
|
|
|
| Несетевая
| 45.8
| 26.4
|
|
|
Определите:
1. По каждой форме торговли относительные изменения (индивидуальные индексы): - цен, - физического объема продажи (в натуральном выражении). 2. В целом по двум формам торговли относительные изменения (общие индексы): - цен (в форме Пааше), - физического объема продажи (в форме Ласпейреса), - товарооборота (в стоимостном выражении). Покажите взаимосвязь между этими индексами.
3. Абсолютное изменение товарооборота - общее и в результате влияния отдельных факторов (изменения цен и изменения физического объема продаж).
4. Индексы средней цены товара "А" переменного и постоянного состава, индекс влияния структурных сдвигов в объеме продаж. Покажите взаимосвязь индексов переменного, постоянного состава и структурных сдвигов.
5. Изменение средней цены товара "А" в абсолютном выражении и влияние на это изменение двух факторов: а) изменение цен, б) изменение структуры объемов продажи. Результаты промежуточных расчетов представьте в табличной форме. Сделайте выводы
1.Расчет индивидуальных индексов
1.1 Для определения относительного изменения цены товара (p) по каждой форме торговли необходимо рассчитать индивидуальные индексы цен (ip) по формуле
i p= 
p0 и p1 – цена товара в базисном и отчетном периодах.
Расчет индивидуальных индексов цен по формуле:
- сетевая торговля: 𝑖𝑝 = 66.2/ 85.6 = 0.77, или 77.3%
- несетевая торговля: 𝑖𝑝 = 26.4/45.8 = 0.57, или 57.6%
Вывод. В сетевой торговле цена на товар «А» снизилась в IV кв. по сравнению с III кв. на -22.7% (77.3-100), что в абсолютном выражении составляет 30 руб.(70- 40), в несетевой - на 76% или на 20 руб.
1.2. Для определения относительного изменения объема продажи товара (q) необходимо рассчитать индивидуальные индексы физического объема (iq) по формуле
𝑖𝑞 = 𝑞1/ 𝑞0
q0 и q1 – количество (физический объем) товара, реализованного в базисном и отчетном периодах.
Расчет индивидуальных индексов физического объема по формуле:
- сетевая торговля: 𝑖𝑞 = 5000/ 4000 = 1,25, или125,0%
несетевая торговля: 𝑖𝑞 = 6000 /5000 = 1,20, или 120,0%
Вывод. В сетевой торговле объем продажи товара «А» вырос в IV кв. по сравнению с III кв. на 25% (125-100), что в абсолютном выражении составляет 1 тыс.кг, в несетевой - на 20% или на 1 тыс.кг.




 *100% следует формула прогнозной оценки на i-ый месяц:
*100% следует формула прогнозной оценки на i-ый месяц:
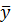 = 36612 / 12 = 3 051 тыс. тонн
= 36612 / 12 = 3 051 тыс. тонн



