Линейное однофакторное уравнение регрессии имеет вид:
yx = a0+a1x1
Коэффициенты уравнения регрессии вычисляются по формулам:
a1 = 
Коэффициенты уравнения регрессии вычисляются по формулам:
А1=  a0=
a0=  - a1
- a1 
Для расчета коэффициентов строится вспомогательная табл.2.2
(расчеты проведены с применением пакета MS Excel):
Таблица 2.2
Расчетная таблица для построения и анализа линейной модели парной регрессии
| №п/п
| x
| y
| x2
| y2
| xy
| ̂yx
| (y- 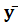 )2 )2
| ˆyx- 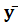
|
|
|
|
|
|
|
| 408,524
| 1513.2
|
|
|
|
|
|
|
|
| 333,852
| 954.8
|
|
|
|
|
|
|
|
| 338,16
| 1082.4
|
|
|
|
|
|
|
|
| 369,034
| 1149.2
| 0.6
|
|
|
|
|
|
|
| 314,466
| 552.3
| 0.6
|
|
|
|
|
|
|
| 372,624
| 342.3
| 0.4
|
|
|
|
|
|
|
| 338,16
| 132.3
| 0.4
|
|
|
|
|
|
|
| 348,212
| 171.6
| 0.4
|
|
|
|
|
|
|
| 364,726
| 182.3
| 0.2
|
|
|
|
|
|
|
| 347,494
| 2.3
| 0.2
|
|
|
|
|
|
|
| 394,164
| 39.7
| 0.2
|
|
|
|
|
|
|
| 348,212
| 3.6
| 0.1
|
|
|
|
|
|
|
| 359,7
| 141.6
| 0.1
|
|
|
|
|
|
|
| 321,646
|
| 0.1
|
|
|
|
|
|
|
| 311,594
| 412.1
|
|
|
|
|
|
|
|
| 372,624
| 151.3
|
|
|
|
|
|
|
|
| 348,212
| 234.1
|
|
|
|
|
|
|
|
| 359,7
| 204.5
|
|
|
|
|
|
|
|
| 328,826
| 835.2
| 0.1
|
|
|
|
|
|
|
| 304,414
| 712.9
| 0,1
|
|
|
|
|
|
|
| 379,804
| 141.6
| 0,2
|
|
|
|
|
|
|
| 369,752
| 141.6
| 0.2
|
|
|
|
|
|
|
| 321,646
| 12.6
| 0.5
|
|
|
|
|
|
|
| 338,16
| 918.1
| 0.5
|
|
|
|
|
|
|
| 304,414
| 2275.3
| 0.5
|
|
|
|
|
|
|
| 358,264
| 2088.5
| 0.5
|
|
|
|
|
|
|
| 348,212
| 670.8
| 0.6
|
|
|
|
|
|
|
| 323,8
| 2275.3
| 0.6
|
|
|
|
|
|
|
| 328,826
| 2883.7
| 1.4
|
|
|
|
|
|
|
| 304,414
| 2777.3
| 2.9
|
| ИТОГО
|
|
|
|
|
|
| 23026.5
| 14.4
|
| Среднее
| 281,07
| 144,3
| 80339,4
| 21832,167
| 41519,767
| -
| 767.6
| 0.5
|
Расчет коэффициентов уравнения регрессии на основе данных табл.: 2.2:
а1=  =0,718
=0,718
а0= 144,3-0,718 = 143,582
Вывод. Линейная регрессионная модель связи изучаемых признаков имеет вид уравнения 𝒚̂𝒙 = 0.02 + 123.9𝒙.
Коэффициент регрессии 𝑎1 = 0,02 показывает, что при увеличении факторного признака Выручка от продажи продукции на 1 млн руб. значение результативного признака Прибыль от продажи продукции увеличивается в среднем на 0,02 млн руб.
3. Проверка уравнения регрессии на адекватность
2. 1. Оценка практической пригодности построенной модели связи 𝒚̂𝒙 = 0.02+123.9𝒙 по величине коэффициента детерминации R 2.
Расчет R2:
𝑅 2 = 
𝑅 2 =14.4/23026.5=0.0006
Вывод. Критерий практической пригодности модели связи R2 > 0,5 не выполняется. Однако поскольку значение R2 практически не совпадает с 0,5, можно считать, что построенное регрессионное уравнение в достаточной мере не отражает фактическую зависимость признаков и не пригодно для практического применения.
2. Оценка статистической значимости (неслучайности) коэффициента R 2 по F-критерию Р.Фишера рассчитывается по формуле:
𝐅𝐑 = 
m – число коэффициентов уравнения регрессии (параметров уравнения регрессии), n- число наблюдений.
Расчет значения F при n=30, m=2:
𝐅𝐑 = 0.0006/1-0.0006*28=0.02
Табличное (критическое) значение F-критерия Fтабл имеет общий вид
𝐹𝛼; 𝑚−1;𝑛−2, где 𝛼- уровень значимости, m– число коэффициентов уравнения регрессии.
При уровне значимости 𝛼 =0,05 и m=2
𝐹𝛼; 𝑚−1;𝑛−2 = 𝐹0,05;1;28 = 4,2
Так как Fрасч>Fтабл (0.02<4.2) то величина найденного коэффициента детерминации R 2 признается неслучайной с вероятностью 0,95.
Вывод. Построенное уравнение регрессии 𝒚̂𝒙 = 0.02+123.9𝒙 нельзя считать адекватным с надежностью 95%.
4. Расчет коэффициента эластичности
𝐾Э = а1  𝐾Э =0.02*270.9/129.3=0,04
𝐾Э =0.02*270.9/129.3=0,04
Вывод. Величина коэффициента эластичности 𝐾Э = 0,04 показывает, что при увеличении факторного признака Выручка от продажи продукции на 1% значение результативного признака Прибыль от продажи продукции увеличивается в среднем на 0,04%.
Задание №3
По результатам выполнения задания 1 с вероятностью 0,954 определите:
1) ошибку выборки средней величины выручки от продажи продукции и границы, в которых будет находиться средняя величина выручки предприятий генеральной совокупности.
2) ошибку выборки доли предприятий с выручкой от продажи продукции более 𝐱̃ млн. руб. (𝐱̃ - средняя величина выручки рассчитанная в задании 1), а также границы, в которых будет находиться генеральная доля.
По условию: выборка 10-процентная, n =30, N=300.
Значения параметров, необходимых для решения задачи и рассчитанных в задании 1, представлены в табл. 3.2:
Таблица 3.2
| Р
| t
| N
| N
| 𝐱̃
| 𝛔2
|
| 0,954
|
|
|
| 272.2
| 1096.4
|




 a0=
a0=  - a1
- a1 
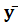 )2
)2
 =0,718
=0,718

 𝐾Э =0.02*270.9/129.3=0,04
𝐾Э =0.02*270.9/129.3=0,04


