

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...
Топ:
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Интересное:
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
1. Простейшие случаи криволинейной корреляции.
Если график регрессии 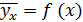 или
или  изображается кривой линией, то корреляцию называют криволинейной.
изображается кривой линией, то корреляцию называют криволинейной.
Например, функции Y на X могут иметь вид:  (параболическая корреляция 2-го порядка);
(параболическая корреляция 2-го порядка);  (параболическая корреляция 3-го порядка).
(параболическая корреляция 3-го порядка).
Для определения вида функции регрессии строят точки (x;  ) и по их расположению делают заключение о примерном виде функции регрессии, принимая во внимание особенности, вытекающие из сущности решаемой задачи.
) и по их расположению делают заключение о примерном виде функции регрессии, принимая во внимание особенности, вытекающие из сущности решаемой задачи.
Неизвестные параметры уравнения регрессии ищут методом наименьших квадратов.
 Рассмотрим, например, выборочное уравнение регрессии Y на X:
Рассмотрим, например, выборочное уравнение регрессии Y на X:  где A,B,C- неизвестные параметры.
где A,B,C- неизвестные параметры.
Пользуясь методом наименьших квадратов, получают систему линейных уравнений относительно неизвестных параметров (вывод аналогичен линейной корреляции).


Найденные из системы параметры подставляют в уравнение (1).



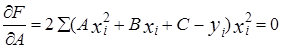

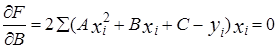

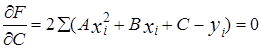
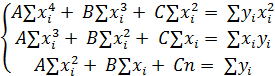
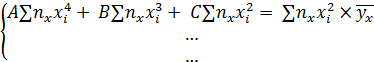
2. Ранговая корреляция, коэффициенты ранговой корреляции Спирмена и Кендалла и их вычисление.
Допустим, что объекты генеральной совокупности обладают двумя качественными признаками, т.е. признаками которые невозможно точно измерить, но они позволяют сравнивать объекты между собой, следовательно, расположить их в порядке убывания или возрастания качества, для определённости в порядке убывания.
Пусть выборка объёма и содержит независимые объекты, которые обладают двумя качественными признаками А и В. Для оценки степени связи признаков вводят коэффициенты ранговой корреляции Спирмена и Кендалла.
Расположим объекты в порядке ухудшения качества, сначала по признаку А. Припишем объекту стоящему на i-м месте, число-ранг xi, равный порядковому номеру объекта: xi=i.
|
|
Затем расположим объекты в порядке убывания по принципу В и припишем каждому из них порядковый номер yi, причём (для удобства сравнения рангов) индекс i при y по-прежнему равен порядковому номеру объекта по признаку А.
В итоге получим две последовательности рангов:
По признаку А x1, x2…xn
По признаку B y1, y2…yn
Для оценки степени связи признаков А и В служат, в частности, коэффициенты ранговой корреляции Спирмена и Кендалла.
Выборочный коэффициент ранговой корреляции Спирмена находят по формуле:
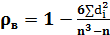 ,
,
где di=xi-yi
n - объём выборки, абсолютная величина  ≤1
≤1
Можно оценивать связь между качественными признаками, используя коэффициент ранговой корреляции Кендалла.
Пусть ранг объектов выборки объёма n
по признаку А x1, x2…xn
по признаку B y1, y2…yn
Допустим, что справа от y1 имеется R1 рангов, больших y1; справа от y2 имеется R2 рангов, больших y2, справа от yn-1 имеется Rn-1 рангов, больших yn-1
Обозначим R= R1+ R2+…Rn-1
Выборочный коэффициент ранговой корреляции Кендалла определяется формулой: 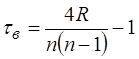
где n-объём выборки 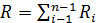
|
|
|

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!