Часто интересующая нас величина представляет собой результат вычисления, полученный из нескольких независимо измеренных величин. Каждая из них содержит погрешность, которая вносит вклад в общую погрешность результата. Это явление называется распространением погрешностей. Конкретный способ распространения погрешностей определяется видом соотношения между исходными и вычисленным значениями. При этом для вычисления случайных и систематических погрешностей используют разные формулы (таблица 4).
Таблица 4 - Распространение погрешностей
| Случай
| Функция
| Систематическая погрешность
| Случайная
погрешность
|
| а
| б
|
|
| u=x+y
| 
| 
| 
|
|
| u=x-y
| 
| 
| 
|
|
| u=xy
| 
| 
| 
|
|
| u=x/y
| 
| 
| 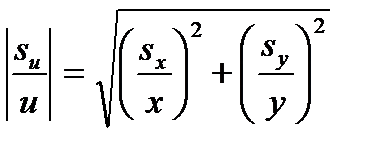
|
|
| u=xp
| 
| 
| 
|
|
| u= ln x
| 
| 
| 
|
|
| u= lg x
| 
| 
| 
|
Как видно из таблицы 4 для линейной функции дисперсия является аддитивной величиной. Вследствие этого наибольшее стандартное отклонение обычно вносит преобладающий вклад в общую величину стандартного отклонения конечного результата. Заметим также, что при вычитании исходных величин их дисперсии все равно складываются.
При расчете систематических погрешностей следует различать два важных случая:
а) Если известны и величины, и знаки погрешностей отдельных составляющих, то расчет суммарной погрешности производится по формулам, приведенным в столбце а таблицы. Величина суммарной погрешности при этом получается с определенным знаком.
б) Если известны лишь максимально возможные погрешности отдельных стадий (это равносильно тому, что известны лишь абсолютные величины, но не знаки этих погрешностей), то расчет производится по формулам указанным в столбце б табл. 4. При этом результат расчета также является абсолютной величиной суммарной погрешности.
Пример. Рассчитайте максимальную систематическую погрешность (абсолютную и относительную) при приготовлении 200,0 см3 раствора с концентрацией с(1/2 Na2C03)=0,1000 моль/дм3. Максимальная систематическая погрешность массы навески ±0,2 мг, калибровки колбы ±0,2 см3. Молярные массы элементов: Na 22,9897; С 12,011; O 15,9994. Погрешности молярных масс элементов считайте равными единице в последнем знаке указанных величин.
Решение: Концентрация раствора в моль/дм3 рассчитывается как

где т - масса навески, г; М - молярная масса эквивалента Na2CО3 =(1/2 M(Na2CО3), г/моль; V -объем раствора, дм3.
В соответствии с законом распространения систематических погрешностей относительная погрешность произведения (частного) равна сумме относительных погрешностей сомножителей (делимого и делителя):
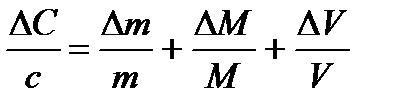
Величина М представляет собой сумму молярных масс элементов:
М= l/2[2M(Na)+M(C)±3M(О)],
поэтому для расчета ∆M также следует применить закон распространения погрешностей: для суммы (разности) величин абсолютная погрешность равна сумме абсолютных погрешностей слагаемых (уменьшаемого и вычитаемого):
∆M = 1/2 [2·10-4 + 1·10-3 + 3·10-4].
Рассчитаем величины М и т:
М= 1/2 (2 • 22,9897 +12,011 + 3 • 15,9994) = 52,9943,
т = сMV = 0,1000· 52,9943 ·0,2000 = 1,0599 (г).
Найдем погрешность ∆M:
∆M =1/2(2·10-4+1·10-3 + 3·10-4) = 7,5·10-4.
Относительная погрешность значения концентрации составляет:
 Абсолютная погрешность составляет:
Абсолютная погрешность составляет:
∆с = 0,1000· 1,2 10-3 = 0,0001 (M).
Контрольное задание № 4
Рассчитайте максимальную систематическую погрешность (абсолютную и относительную) при приготовлении V см3 раствора с концентрацией «с» моль/дм3. Максимальная систематическая погрешность массы навески ±0,2 мг, калибровки колбы ±0,2 см3. Молярные массы элементов – по таблице Д.И. Менделеева.
Погрешности молярных масс элементов считайте равными единице в последнем знаке указанных величин.
Таблица 5 - Исходные данные контрольного задания № 4
| Вариант №
| Вещество
| Объем раствора
V, см3
| Концентрация
раствра
с, моль/дм3
|
|
| Na2SO4
|
| 0,1
|
|
| NaCl
|
| 0,2
|
|
| Na3PO4
|
| 0,5
|
|
| NaBr
|
| 0,1
|
|
| NaI
|
| 0,2
|
|
| Ca(OH)2
|
| 0,5
|
|
| KCl
|
| 0,1
|
|
| KNO3
|
| 0,2
|
|
| NaNO3
|
| 0,5
|
|
| NH4Cl
|
| 0,1
|
|
| CH3COONa
|
| 0,2
|
|
| K2SO4
|
| 0,5
|
|
| K2CO3
|
| 0,1
|
|
| NH4Cl
|
| 0,2
|
|
| KBrO3
|
| 0,5
|
|
| KMnO4
|
| 0,1
|
|
| KH2PO4
|
| 0,2
|
|
| H2C2O4
|
| 0,5
|
|
| Na2C2O4
|
| 0,1
|
|
| NH4SCN
|
| 0,2
|
|
| Na2S2O3· 5H2O
|
| 0,5
|
|
| NH4Br
|
| 0,1
|
|
| NaHCO3
|
| 0,2
|
|
| NaNO2
|
| 0,5
|
|
| Na2B4O7·10H2O
|
| 0,1
|















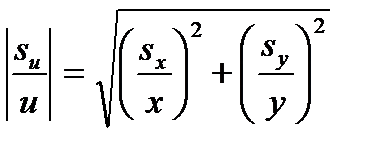










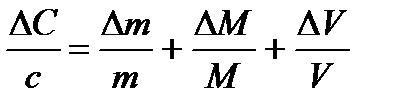
 Абсолютная погрешность составляет:
Абсолютная погрешность составляет:

