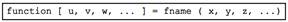Математическая постановка задачи регрессии и ее решение в среде MathCAD

При обработке экспериментальных данных в Mathcad с целью исследования их природы, возникает необходимость выразить зависимую переменную в виде некоторой математической функции от одной или нескольких независимых переменных. Данная зависимость получила название регрессионная модель или уравнение регрессии, а методы, позволяющие получить эту зависимость, принято называть методами регрессионного анализа в Mathcad. Методы регрессионного анализа позволяют: производить расчет различного вида регрессионных моделей; проверять гипотезу адекватности модели имеющимся наблюдениям; использовать модель для прогнозирования значений зависимой переменной при новых значениях независимой переменной. В Mathcad существует набор функций, позволяющих рассчитать различные регрессионные модели. В таблице представлены функции, используемые при создании регрессионных моделей.

Рассмотрим суть параметров, используемых в качестве аргументов в функциях. В каждой функции в Mathcad используются два вектора исходных данных, vx - вектор независимых переменных, vy - вектор зависимых переменных. Количество элементов вектора vx и vy должно быть одинаково. Функции regress и loess используются только совместно с функцией interp. Сами функции regress и loess вычисляют только вектор, требуемый функцией interp для определения самого полинома. В Mathcad параметр span функции loess определяет величину области, на которой строится конкретный фрагмент полинома 2-ой степени. Оптимальное значение span, предлагаемое справочной системой Mathcad, равно 0.75, но в каждом конкретном случае рекомендуется путем вариантных расчетов подобрать наилучшее значение span. Параметр g является вектором начальных приближений для неизвестных функции регрессии. После определения регрессионных зависимостей в Mathcad, актуальным является выбор из их совокупности наилучшей функции, с точки зрения адекватности описания исходных экспериментальных данных. В качестве критерия, позволяющего выбрать наилучшую регрессионную модель, предлагается использовать коэффициент детерминации, численно равный коэффициенту корреляции в квадрате. Значение коэффициента корреляции в Mathcad позволяет рассчитать функция corr(A,B), где A и B – два вектора значений. На листинге, представлен пример расчета различных регрессионных моделей и выбора наилучшей из них. Как видно из данных, приведенных на листинге наилучшие результаты дает полиномиальная модель на основе функции loess. Данная модель характеризуется значением коэффициента детерминации равным 0.984.

Пример:

 

14 – Математическая постановка задачи регрессии и ее решение в среде MatLAB

Полиномиальная регрессия

Одна из наиболее известных аппроксимаций — полиномиальная. В системе MATLAB определены функции аппроксимации данных полиномами по методу наименьших квадратов — полиномиальной регрессии. Это выполняет функция, приведенная ниже:

polyfit(x.y.n) — возвращает вектор коэффициентов полинома р(х) степени п, который с наименьшей среднеквадратичной погрешностью аппроксимирует функцию у(х). Результатом является вектор-строка длиной n+1, содержащий коэффициенты полинома в порядке уменьшения степеней х и у равно n+1, то реализуется обычная полиномиальная аппроксимация, при которой график полинома точно проходит через узловые точки с координатами (х.у), хранящиеся в векторах х и у. В противном случае точного совпадения графика с узловыми точками не наблюдается;

[p.S] = polyflt(x.y.n) — возвращает коэффициенты полинома р и структуру S для использования вместе с функцией polyval с целью оценивания или предсказания погрешности;

[p.S] = polyf1t(x,y,n,mu) возвращает коэффициенты полинома р и структуру S для использования вместе с функцией polyval с целью оценивания или предска-зния погрешности, но так, что присходит центрирование (нормирование) и масштабирование х, xnorm = (х - mu(l))/mu(2), где mu(l) = mean(x) и mu(2) = std(x). Центрирование и масштабирование не только улучшают свойства степенного многочлена, получаемого при помощи polyval, но и значительно повышают качественные характеристики самого алгоритма аппроксимации.

Пример MATLAB:

Пример (полиномиальная регрессия для функции s

» х=(-3:0.2:3)';

y=sin(x);

p=polyflt(x,y,3)

р =

-0.0953 0.0000 0.8651 -0.0000

»x=(-4:0.2:4)';y=sin(x);

» f=polyval(p,x);plot(x,y,'o',x,f)

Рисунок построенный в этом примере, дает наглядное представление о точности полиномиальной аппроксимации. Следует помнить, что она достаточно точна в небольших окрестностях от точки х = 0, но может иметь большие погрешности за их пределами или в промежутках между узловыми точками.

График аппроксимирующего полинома третьей степени на рисунке показан сплошной линией, а точки исходной зависимости обозначены кружками.

 

Управление вычислительным процессом в MatLAB. Примеры

Для организации вычислительного процесса, который записывается в виде некоторого текста программы, необходимы операторы управления.

При этом к операторам управления вычислительным процессом обычно относят операторы безусловного перехода, условных переходов (разветвления вычислительного процесса) и операторы организации циклических процессов. Однако система MATLAB построена таким образом, что эти операторы могут быть использованы и при работе MATLAB в режиме калькулятора.

Оператор условного перехода

Конструкция оператора перехода по условию в общем, виде такова:

if <условие>

<операторы 1>

else

<операторы 2>

end

Работает он следующим образом. Вначале проверяется, выполняется

ли указанное условие. Если да, то программа выполняет совокупность опе-

раторов, которая записана в разделе <операторы 1>. В противном случае

выполняется последовательность операторов раздела <операторы 2>.

Укороченная форма условного оператора имеет вид:

if <условие>

<операторы>

end

Действие оператора в этом случае аналогично, за исключением того, что при невыполнении заданного условия выполняется оператор, следующий за оператором end.

качестве условия используется выражение типа:

<имя переменной 1> <операция сравнения> <имя переменной 2>

Операции сравнения в языке MATLAB могут быть такими:

< меньше;

> больше;

<= меньше или равно;

>= больше или равно;

= равно;

~= не равно.

Условие может быть составным, т.е. складываться из нескольких

простых условий, объединяемых знаками логических операций. Знаками

логических операций в языке MATLAB являются:

& - логическая операция И (AND);

| - логическая операция ИЛИ (OR);

~ - логическая операция НЕТ (NOT).

Логическая операция Исключающее ИЛИ может быть реализована

при помощи функции хог(А,В), где А и В - некоторые условия.

Допустима еще одна конструкция оператора условного перехода.

if <условие 1>

<операторы 1>

elseif <условие 2>

<операторы 2>

elseif <условие З>

<операторы З>

…..

else

<операторы>

end

Оператор elseif выполняется тогда, когда <условие 1> не выполнено. При этом сначала проверяется <условие 2>. Если оно выполнено, выполняются <операторы 2>, если же нет, то <операторы 2> игнорируются и происходит переход к следующему оператору elseif, т.е. к проверке <условия З>. Аналогичным образом при его выполнении обрабатываются <операторы З>, в противном случае происходит переход к следующему оператору elseif. Если ни одно из условий в операторах elseif не выполнено, обрабатываются <операторы>, следующие за оператором else. Таким образом может быть обеспечено ветвление программы по нескольким направлениям.

Пример:

function ifdem(a)

% пример использования структуры if-elseif-else

if (a ==0)

disp('a - ноль')

elseif a==1

disp('a - единица')

elseif a>=2

disp('a - двойка или больше')

else

disp('a меньше двух, но не ноль и не единица')

end

 

 

Оператор переключения

Оператор переключения имеет такую структуру:

switch <выражение, скаляр или строка символов>

сазе <значение 1>

<операторы 1>

сазе <значение 2>

<операторы 2>

….

otherwise

<операторы>

end

Он осуществляет ветвление вычислений в зависимости от значений некоторой переменной или выражения, сравнивая значение полученное в результате вычисления выражения в строке switch, со значениями, указанными в строках со словом case. Соответствующая группа операторов case выполняется, если значение выражения совпадает со значением, указанным в соответствующей строке case. Если значение выражения не совпадает ни с одним из значении в группах case, выполняются операторы, следующие за otherwise.

Пример:

function switchdem(a)

% пример использования оператора switch switch a

case 3 disp('Март')

case 4 disp('Апрель')

case 5 disp('Май')

case {1, 2, 6, 7, 8, 9, 10, 11, 12} disp('Не весенние месяцы')

otherwise

disp('Ошибка задания')

end

Операторы цикла

В языке MATLAB есть две разновидности операторов цикла - услов-

ный и арифметический.

Оператор цикла с предусловием имеет вид:

while <условие>

<операторы>

end

Операторы внутри цикла обрабатываются лишь в том случае, если выполнено условие, записанное после слова while. При этом среди операторов внутри цикла обязательно должны быть такие, которые изменяют значения одной из переменных, указанных в условии цикла.

Приведем пример вычисления значения синуса при 5 значениях аргумента от 0,2 до 1 с шагом 0,2:

Обратите внимание на то, какими средствами в приведенном примере обеспечен вывод на экран нескольких переменных в одну строку.

Для этого, используется оператор disp. Но, в соответствии с правилами применения этого оператора, в нем должен быть только один аргумент (текст, переменная или матрица). Чтобы обойти это препятствие, нужно несколько числовых переменных объединить в единый объект - векторстроку, а последнее легко выполняется при помощи обычной операции формирования вектора-строки из отдельных элементов.

[х1, х2,..., хN]

Таким образом, с помощью оператора вида:

disp([xl, x2,..., xN])

можно обеспечить вывод результатов вычислений в виде таблицы данных.

Арифметический оператор цикла имеет вид:

for <Имя> = <НЗ>:<Ш>:<КЗ>

<операторы>

End

где <Имя> - имя управляющей переменной цикла - счетчика цикла; <НЗ> - заданное начальное значение этой переменной; <Ш> - значение шага, с которым она должна изменяться; <КЗ> - конечное значение переменной цикла. В этом случае <операторы> внутри цикла выполняются несколько раз (каждый раз при новом значении управляющей переменной) до тех пор, пока значение управляющей переменной не выйдет за пределы интервала между <НЗ> и <КЗ>. Если параметр <Ш> не указан, по умолчанию его значение принимается равным единице.

Чтобы досрочно выйти из цикла (например, при выполнении некоторого условия), применяют оператор break. Если в программе встречается этот оператор, выполнение цикла досрочно прекращается и начинает выполняться следующий после слова end оператор.

Для примера используем предыдущее задание:

 

Функции функций

Некоторые важные универсальные процедуры в MATLAB используют в качестве переменного параметра имя функции, с которой они оперируют, и потому требуют при обращении к ним указания имени М-файла, в котором записан текст программы вычисления некоторой другой процедуры (функции). Такие процедуры называют функциями функций.

Чтобы воспользоваться такой функцией от функции, необходимо, чтобы пользователь предварительно создал М-файл, в котором вычислялось бы значение нужной функции по заданному значению ее аргумента. Перечислим некоторые из стандартных функций от функций, предусмотренных в MATLAB.

Вычисление интеграла методом квадратур осуществляется процедурой:

[I, cnt] = quad('<Имя функции>', a,b)

Здесь а и b - нижняя и верхняя границы изменения аргумента функции; I - полученное значение интеграла; cn- число обращений к вычислению функции, представленной М-файлом с названием, указанным в <Имя функции>. Функция quad использует квадратурные формулы Ньютона-Котеса четвертого порядка. Аналогичная процедура quad8 использует более точные формулы 8-го порядка. Интегрирование обыкновенных дифференциальных уравнений осуществляют функции ode23 и ode45. Они могут применяться как для решения простых дифференциальных уравнений, так и для моделирования сложных динамических систем.

Известно, что любая система обыкновенных дифференциальных уравнений (ОДУ) может быть представлена в так называемой форме Коши.

где у - вектор переменных состояния системы; t - аргумент (обычно время);

f - нелинейная вектор-функция от переменных состояния у и аргумента t.

Обращение к процедурам численного интегрирования ОДУ имеет вид:

[t, у] = оdе23('<Имя функции>', tspan, y0, options)

[t, у] = оdе45('<Имя функции>', tspan, y0, options),

где <Имя функции> - строка символов, являющаяся именем М-файла, в котором вычисляется вектор-функция f(y,t), т.е. правые части системы ОДУ;

у0 - вектор начальных значений переменных состояния;

t - массив значений аргумента, соответствующих шагам интегрирования;

у - матрица проинтегрированных значений фазовых переменных, в которой каждый столбец соответствует одной из переменных состояния, а строка содержит значения переменных состояния, соответствующих определенному шагу интегрирования;

tspan - вектор-строка [t0 tfinal], содержащая два значения. t0 – начальное значение аргумента t;

tfinal - конечное значение аргумента, options - строка параметров, определяющих значения допустимой относительной и абсолютной погрешности интегрирования.

Параметр options можно не указывать. Тогда по умолчанию допустимая относительная погрешность интегрирования принимается равной 1.0е-3, а абсолютная (по каждой из переменных состояния) - 1.0е-6. Если же эти значения не устраивают пользователя, то следует перед обращением к процедуре численного интегрирования установить новые значения допустимых погрешностей с помощью процедуры odeset таким образом:

орtions = odeset('RelTol',le-4, 'AbsTol', [le-4 le-4 le-5]).

Параметр RelTol определяет относительную погрешность численного интегрирования по всем переменным одновременно, а AbsTol является вектором-строкой, состоящим из абсолютных допустимых погрешностей численного интегрирования по каждой из фазовых переменных.

Функция ode23 осуществляет интегрирование численным методом Рунге-Кутта 2-го порядка, а с помощью метода 3-го порядка контролирует относительные и абсолютные ошибки интегрирования на каждом шаге и изменяет величину шага интегрирования так, чтобы обеспечить заданные пределы ошибок интегрирования. Для функции ode45 основным методом интегрирования является метод Рунге-Кутта 4-го порядка, а величина шага контролируется методом 5-го порядка.

Далее при рассмотрении расчетов переходных процессов в линейных электрических цепях мы рассмотрим применение данного способа решения дифференциальных уравнений на примере.

Вычисления минимумов и корней функции осуществляется следующими функциями MATLAB.

fmin - нахождение минимума функции одного аргумента;

fmins - нахождение минимума функции нескольких аргументов;

fzero - нахождение нулей (корней) функции одного аргумента.

Последняя из указанных функций может с успехом использоваться для отыскания корней характеристических уравнений при расчете переходных процессов, расчете фильтров и т.д.

Обращение к первой из процедур в общем случае имеет вид.

Xmin = fmin('<Имя функции>', XI, Х2)

Результатом этого обращения будет значение Xmin аргумента функции, соответствующее локальному минимуму в интервале Х1<Х<Х2 функ-

ции, заданной М-файлом с указанным именем. В качестве примера рассмотрим нахождение числа π, как значения локального минимума функции

у = cos(x) на отрезке [3, 4]:

» Xmin = fmin('cos',3,4)

Xmin = 3.1416е+000

Обращение ко второй процедуре должно иметь форму:

Xmin = fmins('<Имя функции>', Х0).

При этом X является вектором аргументов, а Х0 означает начальное

(исходное) значение этого вектора, в окрестности которого отыскивается ближайший локальный минимум функции, заданной М-файлом с указанным именем. Функция fmins находит вектор аргументов Xmin, соответствующий найденному локальному минимуму.

Обращение к функции fzero должно иметь вид:

z = fzero('<Имя функции>', х0, to1, trace)

Здесь х0 — начальное значение аргумента, в окрестности которого отыскивается действительный корень функции со значениями, вычисляемыми в М-файле с заданным именем; tol -_ заданная относительная погрешность вычисления корня; trace -. обозначение необходимости выводить на экран промежуточные результаты; z — значение искомого корня.

Построение графиков функции одной переменной может быть осуществлено при помощи процедуры fplot. Отличие ее от процедуры plot, состоит в том, что для построения графика функции нет необходимости в

предварительном вычислении ее значения и аргумента. Обращение к ней имеет вид:

fplot('<Имя функции>', [<интервал>], n),

где <интервал> - это вектор-строка из двух чисел, задающих, соответственно, нижнюю и верхнюю границы изменения аргумента;

<Имя функции> - имя М-файла с текстом процедуры вычисления значения желаемой функции по заданному значению ее аргумента;

n - количество частей, на которые будет разбит указанный интервал.

Если последнюю величину не указать, по умолчанию интервал разобьется на 25 частей. Несмотря на то, что количество частей n указано, число значений вектора х может быть значительно большим, за счет того, что

функция fplot проводит вычисления с дополнительным ограничением, чтобы приращение угла наклона графика функции на каждом шаге не превышало 10 градусов. Если же оно оказалось большим, осуществляется дробление шага изменения аргумента, но не более чем в 20 раз. Последние

два числа (10 и 20) могут быть изменены пользователем, для этого при обращении следует добавить эти новые значения в заголовок процедуры в

указанном порядке.

Если обратиться к этой процедуре так:

[х, V] = fplot(' <Имя функции ', [<интервал>], n),

то график указанной в М-файле функции не отображается на экране (в графическом окне). Вместо этого вычисляется вектор х аргументов и вектор (или матрица) Y соответствующих значений указанной функции. Чтобы при обращении последнего вида построить график, необходимо сделать это в дальнейшем с помощью процедуры plot(x,Y).

Пример:

k=menu('Выберите задание','Задание 1','Задание 2','Задание 3','Задание 4')

if k==1

clc,clear

x =-pi:0.1:pi;

y=sin(x)+0.3*cos(7*x);

y2=0.5+sin(x)+0.3*cos(7*x);

y3=sin(x)+0.3*cos(7*x)-0.5;

plot(x,y,'.b',x,y2,'*m',x,y3,'-y')

grid on

xlabel('x')

ylabel('y')

title('funkziya')

end

if k==2

clc,clear

x=0.01:1000;

y=(-atan(5*x)-atan(2*x));

subplot(2,1,1),plot(x,y)

subplot(2,1,2),semilogx(x,y)

end

if k==3

clc,clear

f=0:0.05:6.28;

y=(sin(2*f)).*(cos(4*f))

z=sin(5*f).*cos(5*f)

c=sin(7*f)

v=sin(12*f)

subplot(2,2,1),polar(f,y)

subplot(2,2,2),polar(f,z)

subplot(2,2,3),polar(f,c)

subplot(2,2,4),polar(f,v)

end

if k==4

clc,clear

x=-2:0.1:2;

y=-2:0.1:2;

[x,y]=meshgrid(x);

z=exp(x).*sin(-x.*x-y.*y)

contour(x,y,z)

plot(x,y,z)

end

 

 

Подпрограммы-функции в MatLAB. Примеры

В большинстве языков программирования различают подпрограммы-функции и подпрограммы-процедуры. Первые обязаны возвращать числовое значение, результат же действия вторых может быть произвольным. В MATLAB нет такого деления, здесь слова подпрограмма, функция и процедура являются синонимами.

Любая подпрограмма в MATLAB состоит из заголовка и тела функции, в котором располагаются исполняемые операторы. Заголовок процедуры должен иметь следующий вид.

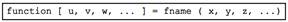
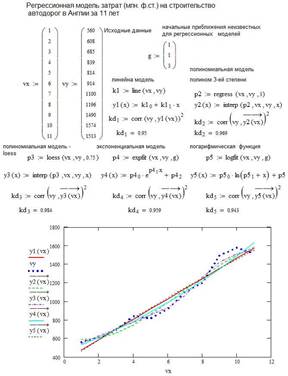
В заголовке процедуры, помимо ключевого слова function и имени функции (fname), перечисляются входные и выходные формальные параметры, которые служат для обмена значениями между процедурой и вызывающей ее программой. Список входных формальных параметров заключается в круглые скобки, а список выходных параметров в квадратные.

При вызове процедуры ей при помощи аргументов (формальных параметров) могут быть переданы некоторые значения (фактические параметры), используемые во время выполнения функции.

После завершения работы процедуры фактические значения присваиваются выходным параметрам. Допускается также существование подпрограмм, не имеющих аргументов и не возвращающих никаких значений. Действие таких подпрограмм может заключаться, например, в выводе на печать некоторых данных и т.п.

При вызове процедуры количество фактических параметров должно обязательно соответствовать числу формальных параметров. При этом соответствующие параметры не обязательно должны быть одинаково обозначены. Формальные параметры, объявленные в заголовке процедуры или функции, рассматриваются как расширение раздела описаний. Их можно использовать в теле подпрограммы как обычные переменные. При вызове процедуры или функции формальные параметры заменяются фактическими.

В простейшем случае у функции есть один входной и один выходной формальный параметр.

%func1.m

function y = func1(x)

y = x.^2;

>> func1(3)

ans =

Список входных формальных параметров может состоять из нескольких

элементов.

%func2.m

function w = func2(x, y, z)

w = x.^2+y.^2+z.^2;

>> func2(1,2,3)

ans =

У процедуры может быть несколько входных и несколько выходных ар-

гументов. Такая ситуация типична для библиотечных функций MATLAB.

%func3.m

function [u, v, w] = func3(x, y)

u = x+y;

v = x.*y;

w = x-y;

>> [a,b,c]=func3(2,3)

a =

b =

c =

-1

Наконец, у процедуры список как входных, так и выходных формальных параметров может быть пустым. В этом случае получение исходных данных для проведения вычислений и вывод полученных результатов может осуществляться исключительно с помощью операций ввода-вывода. Такая процедура отличается от программы на языке MATLAB только областью видимости своих переменных.

%func4.m

function func4 x = input(’Введите x: ’);

y = x.^2+1;

disp(y);

>> func4

Введите x: 3

В одном m-файле может быть расположено сразу несколько процедур,

но при этом из командного окна можно будет обратиться только к той

из них, имя которой совпадает с именем m-файла. Все остальные функ-

ции называются внутренними и могут быть вызваны только из главной

процедуры.

%main.m

function main

x = input(’Введите x: ’);

if x>0

y = f1(x);

else

y = g1(x);

end

disp(y);

function y = f1(x);

y = x+1;

function y = g1(x);

y = x-1;

>> main

Введите x: 5

>> main

Введите x: -5

y =

-6

В том случае если процедура не содержит операторов управления и ввода-вывода, она может быть определена в качестве встраиваемой функции. Встраиваемая функция создается с помощью процедуры inline непосредственно в командном окне и часто называется inline-функцией. У inline-функцией может быть только один выходной параметр, совпадающий с именем самой функции.

Определяющее функцию выражение expr и имена аргументов arg1, arg2 и т.д. переда ются в процедуру inline в виде строк.

>> f = inline(’sin(x.^2+y.^2)’, ’x’, ’y’)

f =

Inline function:

f(x,y) = sin(x.^2+y.^2)

>> f(2,3)

ans =

0.4202