Цель работы: Освоить методику расчета дифференциальной функции и ее графического построения
1 Содержание работы: Определить дифференциальную функцию ЗНР. Определить дифференциальную функцию ЗВР. Построить график дифференциальной функции в зависимости от значений середины интервала 
2 Методические указания
Теоретический закон распределения (TЗP) выражает общий характер изменения показателя надежности (ПН) машин и исключает частные отклонения, связанные с недостатками первичной информации. Процесс замены опытных закономерностей теоретическими называется в теории вероятностей процессом выравнивания (сглаживания) статистической информации.
2.1 Опишите функциональные и вероятностно-статистические подходы оценки надёжности.
2.2 Укажите статистические и функциональные методы определения параметров и причин отказов
2.3 Определение и построение дифференциальная функция теоретического закона распределения
3.Определение дифференциальной функции теоретического закон распределения
Для ЗНР.
Дифференциальную функцию или плотность вероятностей определяют по уравнению (2):
 (1)
(1)
где А -величина интервала;
σ – среднее квадратическое отклонение;
 – середина i-го интервала;
– середина i-го интервала;
 – среднее значение показателя надежности;
– среднее значение показателя надежности;
 – так называемая центрированная дифференциальная функция. Она табулирована и ее значение определяют по приложению А, учитывая при этом, что
– так называемая центрированная дифференциальная функция. Она табулирована и ее значение определяют по приложению А, учитывая при этом, что
 (2)
(2)
Подставляя в формулу (17) исходные данные из таблицы 3 для нашего примера: А=1500 мото-ч, σ = 2130 мото-ч,  = 1650 мото-ч;
= 1650 мото-ч;  = 4420 мото-ч, определим значение дифференциальной функции
= 4420 мото-ч, определим значение дифференциальной функции  для первого интервала:
для первого интервала:
 .
.
Пользуясь таблицей приложения А, находим  =0,17. Тогда
=0,17. Тогда  .
.
Аналогично определяем значение дифференциальной функции для остальных интервалов. Результаты расчета заносим в таблицу 5.
Для ЗРВ.
Дифференциальную функцию или плотность вероятностей определяют по уравнению:
 , (3)
, (3)
где  -середина i-го интервала
-середина i-го интервала
а – параметр ЗРВ, определяемый по формуле:
 , (4)
, (4)
где  - среднее значение показателя надежности;
- среднее значение показателя надежности;
с - сдвиг начала рассеивания показателя надежности;
КВ- коэффициент ЗРВ, определяется по приложению Е в зависимости от коэффициента вариации;
b - параметр ЗРВ. Определяется по приложению И в зависимости от V.
Таблица 5 Сводная таблица опытных и теоретических (3HP и ЗРВ) распределений полных pecypcов двигателей
| | 
| Дифференциальная функция
| Интегральная функция
|
| | ЗНР
| ЗРВ
| ЗНР
| ЗРВ
|
| 1,65
| 0,12
| 0,14
| 0,17
| 0,18
| |
| 3,15
| 0,24
| 0,29
| 0,40
| 0,43
| |
| 4,65
| 0,28
| 0,27
| 0,68
| 0,70
| |
| 6,15
| 0,26
| 0,17
| 0,88
| 0,87
| |
| 7,65
| 0,08
| 0,09
| 0,97
| 0,96
| |
| 9,15
| 0,02
| 0,04
| 1,0
| 1,0
| |
| | | | | | | | | | | |
Для нашего примера:  =4,42 мото-ч; с = 0;V = 0,48; b = 2,2;
=4,42 мото-ч; с = 0;V = 0,48; b = 2,2; 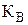 = 0,89 (приложение И).
= 0,89 (приложение И).
Тогда по формуле (4)
 .
.
Параметр «а» также можно приближенно определить по формуле (2);
 , (5)
, (5)
где σ - среднее квадратичное отклонение;
 - коэффициент закона распределения Вейбулла (3PB), определяется по приложению Л в зависимости от коэффициента вариации V.
- коэффициент закона распределения Вейбулла (3PB), определяется по приложению Л в зависимости от коэффициента вариации V.
Для нашего примера: V= 0,48;  = 0,425; σ = 2,13. Тогда по формуле (12):
= 0,425; σ = 2,13. Тогда по формуле (12):
 .
.
Подставляя в формулу (19) полученные для нашего примера значения параметров 3PB а = 5; b = 2,2 м и величину (таблица 3), получим значения дифференциальной функции 3PB для середины каждого интервала.
Например, для первого интервала по формуле (19) имеем:
 .
.
Аналогично определяем значение дифференциальной функции теоретического закона распределения Вейбулла (ЗРВ) для остальных интервалов.
Используя данные таблицы 5 построим дифференциальную функцию ЗНР и ЗРВ, в соответствии с рисунком 3.
При наличии интегральной функции ЗРВ дифференциальная функция  в i-том интервале статистического ряда может быть получена как разность интегральных функций в конце н начале этого интервала:
в i-том интервале статистического ряда может быть получена как разность интегральных функций в конце н начале этого интервала:
 , (6)
, (6)
где  ,
, 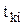 ,
,  ,— значения показателя надежности соответственно в середине, в конце и начале i-го интервала.
,— значения показателя надежности соответственно в середине, в конце и начале i-го интервала.
 tci
tci
Рисунок 3 Дифференциальная функция теоретического закона распределения 3HP (1) и ЗРВ (2) полного ресурса двигателей.
Например, для второго и последующих интервалов дифференциальная функция 3PB по уравнению (6) составит:

Для первого интервала значение дифференциальной функции определяется по уравнению (3) или определяется с использованием таблиц для расчета показателей надежности из приложений.
4 Контрольные вопросы
4.1 Интегральные и дифференциальные формы закона распределения времени работы изделия до отказа.
4.2 Определение долговечности ремонтопригодности и сохраняемости и их основные показатели. Комплексные показатели готовности.
Практическое занятие № 7




 (1)
(1) – середина i-го интервала;
– середина i-го интервала; – среднее значение показателя надежности;
– среднее значение показателя надежности; – так называемая центрированная дифференциальная функция. Она табулирована и ее значение определяют по приложению А, учитывая при этом, что
– так называемая центрированная дифференциальная функция. Она табулирована и ее значение определяют по приложению А, учитывая при этом, что (2)
(2) для первого интервала:
для первого интервала: .
. =0,17. Тогда
=0,17. Тогда  .
. , (3)
, (3) , (4)
, (4) - среднее значение показателя надежности;
- среднее значение показателя надежности;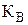 = 0,89 (приложение И).
= 0,89 (приложение И). .
. , (5)
, (5) - коэффициент закона распределения Вейбулла (3PB), определяется по приложению Л в зависимости от коэффициента вариации V.
- коэффициент закона распределения Вейбулла (3PB), определяется по приложению Л в зависимости от коэффициента вариации V. .
. .
. , (6)
, (6)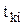 ,
,  ,— значения показателя надежности соответственно в середине, в конце и начале i-го интервала.
,— значения показателя надежности соответственно в середине, в конце и начале i-го интервала. tci
tci



