Решение: если расход металла на швы не учитывать, а толщину стенок, дна и крышки считать одинаковой, то за параметр, определяющий расход металла на изготовление сосуда, принять площадь S его поверхности.
Обозначим размеры сосуда через x, y, z и пусть  z=ky, то получим:
z=ky, то получим:
 , где a=2k,
, где a=2k,  .
.
Функция S имеет наименьшее значение при  и что решение задачи задаётся формулами
и что решение задачи задаётся формулами
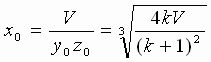 ,
,  ,
,  .
.
Прямоугольные сосуды различной ёмкости производятся в стране в огромных количествах, то становится очевидным, что отступление от оптимальных размеров приводит к значительным убыткам.
Приведем условия задач и дополнительные задания к ним, позволяющие акцентировать внимание на динамическом характере математической модели, выработать первоначальные навыки уточнения модели. Такого рода упражнения могут быть использованы по усмотрению учителя при закреплении умений, связанных с решением задач одномерной оптимизации в домашних, самостоятельных, проверочных и других работах.
Задача № 10.
В начале боя, в игре "Мир танков", у каждой стороны было по 14 боевых машин. В итоге, после захвата базы, потери противника оказались втрое больше потерь вашей команды, и на поле в общей сложности осталось
12 машин. Сколько танков осталось у вашей команды к концу боя?
Составим математическую модель.
В начале игры на поле было 14 • 2 = 28 танков.
Примем за x количество танков потерянных вашей командой,
значит, потери врагов составят 3x.
1. x — ваши потери;
2. 3x — потери вражеской команды;
3. 28 — кол-во всех танков до боя;
4. 12 — кол-во всех танков после боя.
Составим уравнение, и решим его.
28 – x – 3x = 12
28 – 12 – x – 3x = 0
28 – 12 = 4x
16 = 4x
x = 4
Найдем ответ на вопрос задачи.
14 – 4 = 10 (танков).
Ответ: 10 танков осталось у нашей команды в конце боя.
Задача № 11.
Геометрически решить задачу линейного программирования:
 ,
,

Решение.
- Строим область допустимых решений, т.е. геометрическое место точек, в котором одновременно удовлетворяются все ограничения данной ЗЛП. Каждое из неравенств системы ограничений нашей задачи геометрически в системе координат (
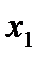 ,
, 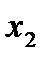 ) определяет полуплоскость соответственно с граничными прямыми.
) определяет полуплоскость соответственно с граничными прямыми.
Первому ограничению соответствует прямая, пересекающая координатные оси в точках с координатами (0, 6) и (6, 0).
Второму ограничению соответствует прямая, пересекающая координатные оси в точках с координатами (0, -1) и (1, 0).
Третьему ограничению соответствует прямая, пересекающая координатные оси в точке с координатами (1, 0) и проходящая параллельно оси 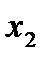 .
.
Четвертому ограничению соответствует прямая, пересекающая координатные оси в точках с координатами (0, 6) и (3, 0).
Пятому ограничению соответствует прямая, пересекающая координатные оси в точках с координатами (0, 4) и (-8, 0).
Шестому ограничению соответствует прямая, пересекающая координатные оси в точке с координатами (0, 1) и проходящая параллельно оси 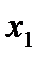 .
.
Области, в которых выполняются соответствующие ограничения в виде неравенств, указаны на рисунке стрелками, направленными в сторону допустимых значений переменных.
Полученная область допустимых решений выделена на рисунке серым цветом.
- Вектор градиента v определяется координатами (0.5, 2). Он перпендикулярен линиям уровня и указывает направление возрастания целевой функции. На рисунке красным цветом изображены линии уровня, заданные уравнениями
 и
и  , т. е. когда целевая функция принимает значение 0 и 10 соответственно.
, т. е. когда целевая функция принимает значение 0 и 10 соответственно.

3. По графику видно, что касание линии уровня (ее уравнение  ), перед выходом из области допустимых решений, произойдет в точке пересечения прямых
), перед выходом из области допустимых решений, произойдет в точке пересечения прямых  и
и 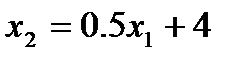 . Нетрудно подсчитать, что эта точка имеет координаты
. Нетрудно подсчитать, что эта точка имеет координаты  .
.
4. В этой точке  значение целевой функции будет наибольшим, т.е.
значение целевой функции будет наибольшим, т.е.
 .
.
Задача № 12.
Решить транспортную задачу.
Транспортная таблица имеет вид:
Решение.
Найдём общую сумму запасов: 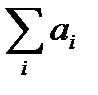 = 70 + 70 + 110 = 250.
= 70 + 70 + 110 = 250.
Найдём общую сумму заявок:  =70 + 90 + 70 + 60 = 290.
=70 + 90 + 70 + 60 = 290.
В нашем случае запасы поставщиков (250 единиц продукции) меньше, чем потребность потребителей (290 единиц продукции) на 40 единиц. Введем в рассмотрение фиктивного поставщика  с запасом продукции, равным 40. Стоимость доставки единицы продукции от данного поставщика ко всем потребителям примем равной нулю.
с запасом продукции, равным 40. Стоимость доставки единицы продукции от данного поставщика ко всем потребителям примем равной нулю.
Решение транспортной задачи начнем с построения допустимого базисного плана, для этого воспользуемся методом северо-западного угла.
Рассмотрим ячейку  таблицы. Запасы поставщика
таблицы. Запасы поставщика  составляют 70 единиц продукции, заявки потребителя
составляют 70 единиц продукции, заявки потребителя  составляет 70. Разместим в ячейку
составляет 70. Разместим в ячейку  значение, равное min { 70, 70 } = 70, т.е. мы полностью израсходoвали запасы поставщика
значение, равное min { 70, 70 } = 70, т.е. мы полностью израсходoвали запасы поставщика  . Вычеркиваем строку 1 таблицы, т.е исключаем ее из дальнейшего рассмотрения. В то же время мы полностью удовлетворили потребность потребителя
. Вычеркиваем строку 1 таблицы, т.е исключаем ее из дальнейшего рассмотрения. В то же время мы полностью удовлетворили потребность потребителя  , но будем считать, что потребность данного потребителя составляют 0 единиц продукции (не будем одновременно вычеркивать строку и столбец).
, но будем считать, что потребность данного потребителя составляют 0 единиц продукции (не будем одновременно вычеркивать строку и столбец).
Рассмотрим ячейку 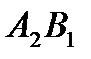 .Запасы поставщика
.Запасы поставщика  составляют 70 единиц продукции. Потребность потребителя
составляют 70 единиц продукции. Потребность потребителя  составляет 0. Разместим в ячейку
составляет 0. Разместим в ячейку 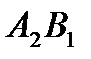 значение, равное min { 70, 0 } = 0,т.е. мы полностью удовлетворили потребность потребителя
значение, равное min { 70, 0 } = 0,т.е. мы полностью удовлетворили потребность потребителя  . Поэтому исключаем 1ый столбец таблицы из дальнейшего рассмотрения.
. Поэтому исключаем 1ый столбец таблицы из дальнейшего рассмотрения.
Рассмотрим ячейку  .Запасы поставщика
.Запасы поставщика 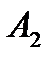 составляют 70 единиц продукции. Потребность потребителя
составляют 70 единиц продукции. Потребность потребителя 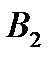 составляет 90. Разместим в ячейку
составляет 90. Разместим в ячейку  значение, равное min { 70, 90 } = 70,т.е. мы полностью израсходoвали запасы поставщика
значение, равное min { 70, 90 } = 70,т.е. мы полностью израсходoвали запасы поставщика 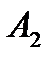 . Вычеркиваем строку 2 таблицы, т.е исключаем ее из дальнейшего рассмотрения.
. Вычеркиваем строку 2 таблицы, т.е исключаем ее из дальнейшего рассмотрения.
Рассмотрим ячейку  .Запасы поставщика
.Запасы поставщика  составляют 110 единиц продукции. Потребность потребителя
составляют 110 единиц продукции. Потребность потребителя 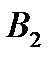 составляет 90 – 70 = 20. Разместим в ячейку
составляет 90 – 70 = 20. Разместим в ячейку  значение, равное min { 110, 20 } = 20,т.е. мы полностью удовлетворили запросы потребителя
значение, равное min { 110, 20 } = 20,т.е. мы полностью удовлетворили запросы потребителя 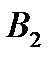 . Поэтому исключаем 2ой столбец таблицы из дальнейшего рассмотрения.
. Поэтому исключаем 2ой столбец таблицы из дальнейшего рассмотрения.
Рассмотрим ячейку  .Запасы поставщика
.Запасы поставщика  составляют 110 – 20 = 90 единиц продукции. Потребность потребителя
составляют 110 – 20 = 90 единиц продукции. Потребность потребителя  составляет 70. Разместим в ячейку
составляет 70. Разместим в ячейку  значение, равное min { 90, 70 } = 70, т.е. мы полностью удовлетворили запросы потребителя
значение, равное min { 90, 70 } = 70, т.е. мы полностью удовлетворили запросы потребителя  . Поэтому исключаем 3ий столбец таблицы из дальнейшего рассмотрения.
. Поэтому исключаем 3ий столбец таблицы из дальнейшего рассмотрения.
Рассмотрим ячейку  . Запасы поставщика
. Запасы поставщика  составляют 90 – 70 = 20 единиц продукции. Потребность потребителя
составляют 90 – 70 = 20 единиц продукции. Потребность потребителя 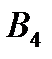 составляет 60. Разместим в ячейку
составляет 60. Разместим в ячейку  значение, равное min { 20, 60 } = 20,т.е. мы полностью израсходoвали запасы поставщика
значение, равное min { 20, 60 } = 20,т.е. мы полностью израсходoвали запасы поставщика  . Поэтому исключаем 3ью строку таблицы из дальнейшего рассмотрения.
. Поэтому исключаем 3ью строку таблицы из дальнейшего рассмотрения.
Рассмотрим ячейку 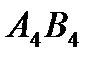 . Запасы поставщика
. Запасы поставщика  составляют 40 единиц продукции. Потребность потребителя
составляют 40 единиц продукции. Потребность потребителя 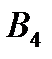 составляет 60 – 20 = 40. Разместим в ячейку
составляет 60 – 20 = 40. Разместим в ячейку 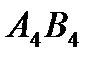 значение, равное min { 40, 40 } = 40,т.е. мы полностью израсходoвали запасы поставщика
значение, равное min { 40, 40 } = 40,т.е. мы полностью израсходoвали запасы поставщика  . Поэтому исключаем 4ую строку таблицы из дальнейшего рассмотрения. В то же время мы полностью удовлетворили запросы потребителя
. Поэтому исключаем 4ую строку таблицы из дальнейшего рассмотрения. В то же время мы полностью удовлетворили запросы потребителя 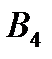 .
.
Мы нашли начальное опорное решение, т.е. израсходовали все запасы поставщиков и удовлетворили все заявки потребителей. Занесем полученные значения в таблицу:
Теперь, произведем его оценку. Общие затраты на доставку всей продукции, для данного решения, составляют
 = 20
= 20  70 + 15
70 + 15  0 + 9
0 + 9  70 + 19
70 + 19  20 + 15
20 + 15  70 + 13
70 + 13  20 + 0
20 + 0  40 = 3720 единиц.
40 = 3720 единиц.
Найдем потенциалы поставщиков  и потребителей
и потребителей  . Примем
. Примем  = 0. Тогда:
= 0. Тогда:
 =
=  -
-  = 19 - 0 = 19
= 19 - 0 = 19
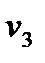 =
= 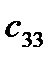 -
-  = 15 - 0 = 15
= 15 - 0 = 15
 =
=  -
-  = 13 - 0 = 13
= 13 - 0 = 13
 =
=  -
-  = 0 - 13 = -13
= 0 - 13 = -13
 =
=  -
-  = 9 - 19 = -10
= 9 - 19 = -10
 =
=  -
-  = 15 – (-10) = 25
= 15 – (-10) = 25
 =
=  -
-  = 20 - 25 = -5
= 20 - 25 = -5
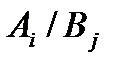
| 
| 
| 
| 
| Запасы 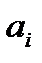
| Потенциалы 
|

|
|
|
|
|
| -5
|

|
|
|
|
|
| -10
|

|
|
|
|
|
|
|

|
|
|
|
|
| -13
|
Заявки 
|
|
|
|
|
|
|
Потенциалы 
|
|
|
|
|
|
|
Найдем оценки свободных ячеек следующим образом:
 =
=  - (
- ( +
+  ) = 13 - (-5 + 19) = -1
) = 13 - (-5 + 19) = -1
 =
=  - (
- ( +
+ 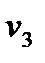 ) = 8 - (-5 + 15) = -2
) = 8 - (-5 + 15) = -2
 =
=  - (
- ( +
+  ) = 11 - (-5 + 13) = 3
) = 11 - (-5 + 13) = 3
 =
=  - (
- ( +
+  ) = 17 - (-10 + 15) = 12
) = 17 - (-10 + 15) = 12
 =
=  - (
- ( +
+  ) = 18 - (-10 + 13) = 15
) = 18 - (-10 + 13) = 15
 =
=  - (
- ( +
+ 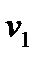 ) = 21 - (0 + 25) = -4
) = 21 - (0 + 25) = -4
 =
=  - (
- (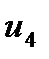 +
+ 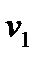 ) = 0 - (-13 + 25) = -12
) = 0 - (-13 + 25) = -12
 =
=  - (
- ( +
+  ) = 0 - (-13 + 19) = -6
) = 0 - (-13 + 19) = -6
 =
=  - (
- ( +
+  ) = 0 - (-13 + 15) = -2
) = 0 - (-13 + 15) = -2
Среди оценок есть отрицательные, следовательно, решение не оптимальное.
Из отрицательных оценок выбираем минимальную, она соответствует ячейке 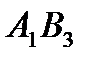 , ее оценка
, ее оценка  = -2.
= -2.
Ячейки  ,
,  ,
,  ,
,  ,
, 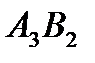 ,
,  образуют цикл для свободной ячейки
образуют цикл для свободной ячейки  . Цикл начинается в этой свободной ячейке. Пусть ячейка
. Цикл начинается в этой свободной ячейке. Пусть ячейка  имеет порядковый номер 1.
имеет порядковый номер 1.
Среди ячеек цикла  ,
,  ,
,  , номера которых четные, выберем ячейку
, номера которых четные, выберем ячейку  , как обладающую наименьшим значением 70. От ячеек цикла с четными номерами, мы отнимаем 70. К ячейкам с нечетными номерами мы прибавляем 70. Ячейка
, как обладающую наименьшим значением 70. От ячеек цикла с четными номерами, мы отнимаем 70. К ячейкам с нечетными номерами мы прибавляем 70. Ячейка  выйдет из базиса, ячейка
выйдет из базиса, ячейка  станет базисной.
станет базисной.
Общие затраты на доставку всей продукции, для данного решения, составляют
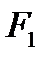 = 8
= 8  70 + 15
70 + 15  70 + 19
70 + 19  90 + 13
90 + 13  20 + 0
20 + 0  40 = 3580 единиц.
40 = 3580 единиц.
Найдем потенциалы поставщиков  и потребителей
и потребителей  . Примем
. Примем  = 0. Тогда:
= 0. Тогда:
 =
=  -
-  = 19 - 0 = 19
= 19 - 0 = 19
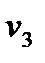 =
= 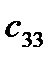 -
-  = 15 - 0 = 15
= 15 - 0 = 15
 =
=  -
-  = 13 - 0 = 13
= 13 - 0 = 13
 =
=  -
-  = 0 - 13 = -13
= 0 - 13 = -13
 =
=  -
-  = 8 - 15 = -7
= 8 - 15 = -7
 =
=  -
-  = 9 - 19 = -10
= 9 - 19 = -10
 =
=  -
-  = 15 – (-10) = 25
= 15 – (-10) = 25
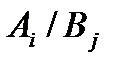
| 
| 
| 
| 
| Запасы 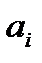
| Потенциалы 
|

|
|
|
|
|
| -7
|

|
|
|
|
|
| -10
|

|
|
|
|
|
|
|

|
|
|
|
|
| -13
|
Заявки 
|
|
|
|
|
|
|
Потенциалы 
|
|
|
|
|
|
|
Найдем оценки свободных ячеек следующим образом:
 =
=  - (
- ( +
+  ) = 20 - (-7 + 25) = 2
) = 20 - (-7 + 25) = 2
 =
=  - (
- ( +
+  ) = 13 - (-7 + 19) = 1
) = 13 - (-7 + 19) = 1
 =
=  - (
- ( +
+  ) = 11 - (-7 + 13) = 5
) = 11 - (-7 + 13) = 5
 =
=  - (
- ( +
+  ) = 17 - (-10 + 15) = 12
) = 17 - (-10 + 15) = 12
 =
=  - (
- ( +
+  ) = 18 - (-10 + 13) = 15
) = 18 - (-10 + 13) = 15
 =
=  - (
- ( +
+ 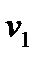 ) = 21 - (0 + 25) = -4
) = 21 - (0 + 25) = -4
 =
=  - (
- (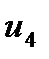 +
+ 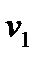 ) = 0 - (-13 + 25) = -12
) = 0 - (-13 + 25) = -12
 =
=  - (
- ( +
+  ) = 0 - (-13 + 19) = -6
) = 0 - (-13 + 19) = -6
Среди оценок есть отрицательные, следовательно, решение не оптимальное.
Из отрицательных оценок выбираем минимальную, она соответствует ячейке  , ее оценка
, ее оценка  = -12.
= -12.
Ячейки  ,
, 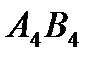 ,
, 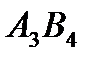 ,
,  ,
,  ,
,  образуют цикл для свободной ячейки
образуют цикл для свободной ячейки  . Цикл начинается в этой свободной ячейке. Пусть ячейка
. Цикл начинается в этой свободной ячейке. Пусть ячейка  имеет порядковый номер 1.
имеет порядковый номер 1.
Среди ячеек цикла 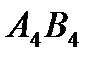 ,
,  ,
,  , номера которых четные, выберем ячейку
, номера которых четные, выберем ячейку 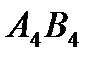 , как обладающую наименьшим значением 40. От ячеек цикла с четными номерами, мы отнимаем 40. К ячейкам с нечетными номерами мы прибавляем 40. Ячейка
, как обладающую наименьшим значением 40. От ячеек цикла с четными номерами, мы отнимаем 40. К ячейкам с нечетными номерами мы прибавляем 40. Ячейка 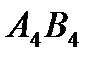 выйдет из базиса, ячейка
выйдет из базиса, ячейка  станет базисной.
станет базисной.
Общие затраты на доставку всей продукции, для данного решения, составляют
 = 8
= 8  70 + 15
70 + 15  30 + 9
30 + 9  40 + 19
40 + 19  50 + 13
50 + 13  60 + 0
60 + 0  40 = 3100 единиц.
40 = 3100 единиц.
Найдем потенциалы поставщиков  и потребителей
и потребителей  . Примем
. Примем  = 0. Тогда:
= 0. Тогда:
 =
=  -
-  = 19 - 0 = 19
= 19 - 0 = 19
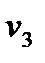 =
= 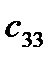 -
-  = 15 - 0 = 15
= 15 - 0 = 15
 =
=  -
-  = 13 - 0 = 13
= 13 - 0 = 13
 =
=  -
-  = 8 - 15 = -7
= 8 - 15 = -7
 =
=  -
-  = 9 - 19 = -10
= 9 - 19 = -10
 =
=  -
-  = 15 – (-10) = 25
= 15 – (-10) = 25
 =
=  -
-  = 0 - 25 = -25
= 0 - 25 = -25
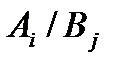
| 
| 
| 
| 
| Запасы 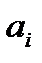
| Потенциалы 
|

|
|
|
|
|
| -7
|

|
|
|
|
|
| -10
|

|
|
|
|
|
|
|

|
|
|
|
|
| -25
|
Заявки 
|
|
|
|
|
|
|
Потенциалы 
|
|
|
|
|
|
|
Найдем оценки свободных ячеек следующим образом:
 =
=  - (
- ( +
+  ) = 20 - (-7 + 25) = 2
) = 20 - (-7 + 25) = 2
 =
=  - (
- ( +
+  ) = 13 - (-7 + 19) = 1
) = 13 - (-7 + 19) = 1
 =
=  - (
- ( +
+  ) = 11 - (-7 + 13) = 5
) = 11 - (-7 + 13) = 5
 =
=  - (
- ( +
+  ) = 17 - (-10 + 15) = 12
) = 17 - (-10 + 15) = 12
 =
=  - (
- ( +
+  ) = 18 - (-10 + 13) = 15
) = 18 - (-10 + 13) = 15
 =
=  - (
- ( +
+ 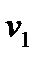 ) = 21 - (0 + 25) = -4
) = 21 - (0 + 25) = -4
 =
=  - (
- ( +
+  ) = 0 - (-25 + 19) = 6
) = 0 - (-25 + 19) = 6
 =
=  - (
- (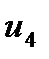 +
+  ) = 0 - (-25 + 15) = 10
) = 0 - (-25 + 15) = 10
 =
=  - (
- (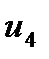 +
+  ) = 0 - (-25 + 13) = 12
) = 0 - (-25 + 13) = 12
Среди оценок есть отрицательные, следовательно, решение не оптимальное.
Из отрицательных оценок выбираем минимальную, она соответствует ячейке 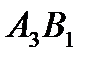 , ее оценка
, ее оценка  = -4. Ячейки
= -4. Ячейки 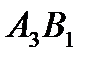 ,
,  ,
,  ,
, 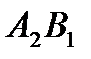 образуют цикл для свободной ячейки
образуют цикл для свободной ячейки 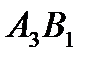 . Цикл начинается в этой свободной ячейке. Пусть ячейка
. Цикл начинается в этой свободной ячейке. Пусть ячейка 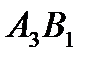 имеет порядковый номер 1.
имеет порядковый номер 1.
Среди ячеек цикла  ,
, 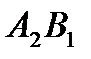 ,номера которых четные, выберем ячейку
,номера которых четные, выберем ячейку 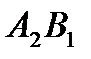 , как обладающую наименьшим значением 30. От ячеек цикла с четными номерами, мы отнимаем 30. К ячейкам с нечетными номерами мы прибавляем 30. Ячейка
, как обладающую наименьшим значением 30. От ячеек цикла с четными номерами, мы отнимаем 30. К ячейкам с нечетными номерами мы прибавляем 30. Ячейка 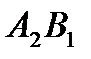 выйдет из базиса, ячейка
выйдет из базиса, ячейка 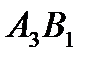 станет базисной.
станет базисной.
Общие затраты на доставку всей продукции, для данного решения, составляют
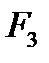 = 8
= 8  70 + 9
70 + 9  70 + 21
70 + 21  30 + 19
30 + 19  20 + 13
20 + 13  60 + 0
60 + 0  40 = 2980 единиц.
40 = 2980 единиц.
Найдем потенциалы поставщиков  и потребителей
и потребителей  . Примем
. Примем  = 0. Тогда:
= 0. Тогда:
 =
=  -
-  = 21 – 0 = 21
= 21 – 0 = 21
 =
=  -
-  = 19 - 0 = 19
= 19 - 0 = 19
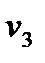 =
= 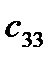 -
-  = 15 - 0 = 15
= 15 - 0 = 15
 =
=  -
-  = 13 - 0 = 13
= 13 - 0 = 13
 =
=  -
-  = 0 - 21 = -21
= 0 - 21 = -21
 =
=  -
-  = 8 - 15 = -7
= 8 - 15 = -7
 =
=  -
-  = 9 - 19 = -10
= 9 - 19 = -10





 z=ky, то получим:
z=ky, то получим: , где a=2k,
, где a=2k,  .
. и что решение задачи задаётся формулами
и что решение задачи задаётся формулами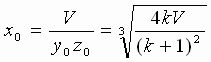 ,
,  ,
,  .
. ,
,
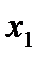 ,
, 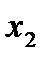 ) определяет полуплоскость соответственно с граничными прямыми.
) определяет полуплоскость соответственно с граничными прямыми. и
и  , т. е. когда целевая функция принимает значение 0 и 10 соответственно.
, т. е. когда целевая функция принимает значение 0 и 10 соответственно.
 и
и 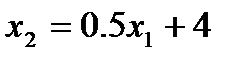 . Нетрудно подсчитать, что эта точка имеет координаты
. Нетрудно подсчитать, что эта точка имеет координаты  .
. значение целевой функции будет наибольшим, т.е.
значение целевой функции будет наибольшим, т.е. .
.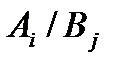




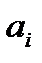




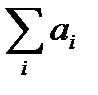 = 70 + 70 + 110 = 250.
= 70 + 70 + 110 = 250. =70 + 90 + 70 + 60 = 290.
=70 + 90 + 70 + 60 = 290. с запасом продукции, равным 40. Стоимость доставки единицы продукции от данного поставщика ко всем потребителям примем равной нулю.
с запасом продукции, равным 40. Стоимость доставки единицы продукции от данного поставщика ко всем потребителям примем равной нулю. таблицы. Запасы поставщика
таблицы. Запасы поставщика  составляют 70 единиц продукции, заявки потребителя
составляют 70 единиц продукции, заявки потребителя 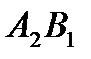 .Запасы поставщика
.Запасы поставщика  составляют 70 единиц продукции. Потребность потребителя
составляют 70 единиц продукции. Потребность потребителя 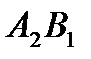 значение, равное min { 70, 0 } = 0,т.е. мы полностью удовлетворили потребность потребителя
значение, равное min { 70, 0 } = 0,т.е. мы полностью удовлетворили потребность потребителя  .Запасы поставщика
.Запасы поставщика 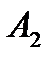 составляют 70 единиц продукции. Потребность потребителя
составляют 70 единиц продукции. Потребность потребителя 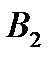 составляет 90. Разместим в ячейку
составляет 90. Разместим в ячейку  .Запасы поставщика
.Запасы поставщика  составляют 110 единиц продукции. Потребность потребителя
составляют 110 единиц продукции. Потребность потребителя  .Запасы поставщика
.Запасы поставщика  составляет 70. Разместим в ячейку
составляет 70. Разместим в ячейку  значение, равное min { 90, 70 } = 70, т.е. мы полностью удовлетворили запросы потребителя
значение, равное min { 90, 70 } = 70, т.е. мы полностью удовлетворили запросы потребителя  . Запасы поставщика
. Запасы поставщика  составляют 90 – 70 = 20 единиц продукции. Потребность потребителя
составляют 90 – 70 = 20 единиц продукции. Потребность потребителя 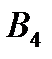 составляет 60. Разместим в ячейку
составляет 60. Разместим в ячейку  . Поэтому исключаем 3ью строку таблицы из дальнейшего рассмотрения.
. Поэтому исключаем 3ью строку таблицы из дальнейшего рассмотрения.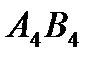 . Запасы поставщика
. Запасы поставщика  составляют 40 единиц продукции. Потребность потребителя
составляют 40 единиц продукции. Потребность потребителя  = 20
= 20  70 + 15
70 + 15  0 + 9
0 + 9  и потребителей
и потребителей  . Примем
. Примем  = 0. Тогда:
= 0. Тогда: =
=  -
- 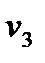 =
= 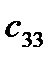 -
-  =
=  -
-  =
=  -
-  = 0 - 13 = -13
= 0 - 13 = -13 =
=  -
-  = 9 - 19 = -10
= 9 - 19 = -10 =
=  -
-  =
=  -
- 
 =
=  - (
- ( +
+  ) = 13 - (-5 + 19) = -1
) = 13 - (-5 + 19) = -1 =
=  - (
- ( =
=  - (
- ( ) = 11 - (-5 + 13) = 3
) = 11 - (-5 + 13) = 3 =
=  - (
- ( +
+  ) = 17 - (-10 + 15) = 12
) = 17 - (-10 + 15) = 12 =
=  - (
- ( =
=  - (
- ( +
+ 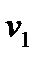 ) = 21 - (0 + 25) = -4
) = 21 - (0 + 25) = -4 =
=  - (
- (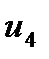 +
+  =
=  - (
- ( +
+  =
=  - (
- (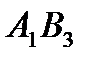 , ее оценка
, ее оценка  = -2.
= -2. ,
,  ,
,  ,
,  ,
, 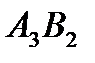 ,
,  образуют цикл для свободной ячейки
образуют цикл для свободной ячейки  , номера которых четные, выберем ячейку
, номера которых четные, выберем ячейку  выйдет из базиса, ячейка
выйдет из базиса, ячейка 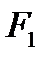 = 8
= 8  -
-  = 8 - 15 = -7
= 8 - 15 = -7 =
=  - (
- ( ) = 20 - (-7 + 25) = 2
) = 20 - (-7 + 25) = 2 , ее оценка
, ее оценка  ,
, 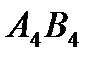 ,
, 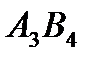 ,
,  ,
,  образуют цикл для свободной ячейки
образуют цикл для свободной ячейки  = 8
= 8  -
-  =
=  - (
- ( =
=  - (
- (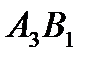 , ее оценка
, ее оценка  ,
,  ,
, 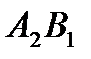 образуют цикл для свободной ячейки
образуют цикл для свободной ячейки  ,
, 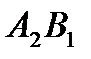 ,номера которых четные, выберем ячейку
,номера которых четные, выберем ячейку 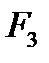 = 8
= 8  -
- 


