Если разложить функцию в ряд и рассмотреть слагаемое со степенью n, то можно сравнить его с теоретически полученным видом  и отсюда извлекается информация о значении
и отсюда извлекается информация о значении  , причём не требуется вычислять все производные включительно до n порядка, а сразу получаем значение n-й производной в точке. Ведь бывает так, что функция содержит произведение, и там число слагаемых удваивается на каждом шаге, и их уже 1024 для 10-й производной.
, причём не требуется вычислять все производные включительно до n порядка, а сразу получаем значение n-й производной в точке. Ведь бывает так, что функция содержит произведение, и там число слагаемых удваивается на каждом шаге, и их уже 1024 для 10-й производной.
Пример. Найти  для
для  .
.
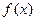 =
=  =
= 
Здесь нам нужен только коэффициент при степени 10.
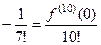

 .
.
Ответ.  .
.
Нахождение определённого интеграла.
Если функция требует больших трудоёмких подстановок, или многократного интегрирования по частям, можно разложить функцию в ряд, состоящий из степенных функций, и приближённо вычислить.
Пример. Приближённо найти интеграл  с точностью
с точностью  .
.
 =
=  =
=  =
=  =
=
 очевидно, здесь 3 и последующие слагаемые заведомо меньше
очевидно, здесь 3 и последующие слагаемые заведомо меньше 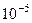 , и не повлияют на 4-й знак после запятой, поэтому приближённое значение
, и не повлияют на 4-й знак после запятой, поэтому приближённое значение
 =
= 

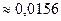 .
.
Как видим, даже 2-е слагаемое можно было не рассматривать, т.к.
оно меньше, чем  .
.
Решение дифференциальных уравнений.
Можно представить неизвестную функцию  в виде степенного ряда
в виде степенного ряда  и подставить его в дифференциальное уравнение, тогда решение найдётся тоже в виде ряда, т.е. можно знать строение решения, его график и т.д. даже без аналитического выражения этой функции..
и подставить его в дифференциальное уравнение, тогда решение найдётся тоже в виде ряда, т.е. можно знать строение решения, его график и т.д. даже без аналитического выражения этой функции..
Пример.  решить с помощью степенных рядов.
решить с помощью степенных рядов.
 тогда
тогда 
Из равенства  =
=  получаем:
получаем:
 ,
,  ,
,  и так далее.
и так далее.
В этом случае все коэффициенты можно последовательно выразить через  . А именно,
. А именно,  ,
,  ,
, 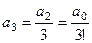 и т.д.
и т.д.
Тогда  =
=  здесь видно, что в скобках получилось разложение экспоненты. Итак,
здесь видно, что в скобках получилось разложение экспоненты. Итак, 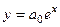 . Эту единственную константу можно переобозначить
. Эту единственную константу можно переобозначить  и получится знакомый из вид общего решения такого уравнения:
и получится знакомый из вид общего решения такого уравнения:  .
.
Пример. Решить дифференциальное уравнение  с помощью степенных рядов.
с помощью степенных рядов.





Подставим в уравнение.
 =
=  тогда:
тогда:
 ,
, 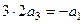 ,
,
 ,
,  ,
,
 ,
,  ,
,
......
Из этих двух групп равенств можно все чётные коэффициенты выразить через  , а все нечётные через
, а все нечётные через  .
.
 ,
, 
 ,
,  ,...
,...
аналогично,  ,
, 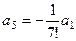 ,
, 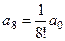 ,
,  ,...
,...
Тогда  =
=
 =
=  .
.
Впрочем, константы можно переобозначить через  и записать решение в привычном виде
и записать решение в привычном виде  .
.
Ряды ЛОРАНА.
Ряд вида  , то есть содержащий как положительные, так и отрицательные целые степени, называется рядом Лорана.
, то есть содержащий как положительные, так и отрицательные целые степени, называется рядом Лорана.
Совокупность слагаемых с нулевой и положительной степенью называется его правильной частью, а отрицательных - главной частью.
 правильная часть,
правильная часть,  главная часть, её также можно переписать в виде:
главная часть, её также можно переписать в виде: 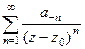 .
.

Теорема 1. Область сходимости ряда Лорана есть кольцо вида  .
.
Доказательство. Распишем по отдельности на главную и правильную часть:  +
+ 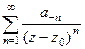 .
.
1. Для правильной части верна теорема Абеля, ведь это обычный степенной ряд. Правильная часть абсолютно сходится в некотором круге  .
.
2. Рассмотрим главную часть ряда Лорана 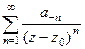 .
.
Сделаем в ней замену с целью представить через положительные степени и применить теорему Абеля.  . тогда для новой переменной
. тогда для новой переменной  ряд принимает такой вид:
ряд принимает такой вид:  . Это степенной ряд, его круг сходимости с центром в 0. То есть,
. Это степенной ряд, его круг сходимости с центром в 0. То есть, 
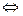

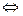
 , обозначим
, обозначим  , вот и получили
, вот и получили 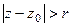 .
.
Итак, область сходимости есть  , это кольцо.
, это кольцо.
Крайние случаи:
Если  : круг с выколотой точкой
: круг с выколотой точкой  .
.
Это происходит, если в главной части лишь конечное количество слагаемых. Их значение не существует только в самой точке 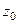 , а в любой точке из её окрестности - существует. Поэтому из области сходимости исключается лишь одна точка.
, а в любой точке из её окрестности - существует. Поэтому из области сходимости исключается лишь одна точка.
Если  : внешняя часть некоторого круга
: внешняя часть некоторого круга  .
.
Пример. Найти кольцо сх ряда Лорана  .
.
Решение. Найдём отдельно по радикальному признаку Коши область сходимости правильной и главной части.
1. Для  получается
получается  , т.е.
, т.е. 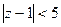
2. Для 
 получается
получается  , т.е.
, т.е.  .
.
Ответ. Кольцо сходимости:  .
.
Приложение 1. Вопросы на доказательства (для билетов).
Лекция № 1
1. Докажите формулу интегрирования по частям.
Лекция № 2
1. Доказать, что замена 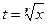 , где r = НОК (r1,...,rk) сводит интеграл
, где r = НОК (r1,...,rk) сводит интеграл 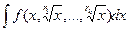 к интегралу от рациональной дроби.
к интегралу от рациональной дроби.
2. Доказать, что замена замена  сводит интеграл вида
сводит интеграл вида  к интегралу от рациональной дроби.
к интегралу от рациональной дроби.
3. Вывести формулы преобразования синуса и косинуса

 для универсальной тригонометрической замены
для универсальной тригонометрической замены  .
.
4. Доказать, что в случае, когда функция нечётна относительно косинуса, замена  сводит интеграл к рациональной дроби.
сводит интеграл к рациональной дроби.
5. Доказать, что в случае, когда 
замена:  сводит интеграл к рациональной дроби.
сводит интеграл к рациональной дроби.
6. Доказать, что для интеграла вида  замена
замена  своит интеграл к рациональной дроби.
своит интеграл к рациональной дроби.
7. Доказать формулу 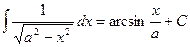
8. Доказать, что для интеграла вида  замена
замена  своит интеграл к рациональной дроби.
своит интеграл к рациональной дроби.
9. Доказать, что для интеграла вида  замена
замена  сводит интеграл к рациональной дроби.
сводит интеграл к рациональной дроби.
Лекция № 3
1. Доказать, что функция  является первообразной от функции
является первообразной от функции 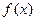 .
.
2. Доказать формулу Ньютона- Лейбница:  .
.
3. Доказать формулу длины явно заданной кривой:
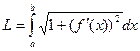 .
.
4. Доказать формулу длины кривой, заданной в полярных координатах 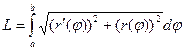
Лекция № 4
Докажите теорему:  сходится
сходится 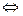
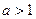 ,
,  сходится
сходится 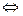
 .
.
Лекция № 5
1. Вывести (доказать) формулу площади явно заданной поверхности  .
.
2. Вывод формул перехода к полярным координатам  .
.
3. Вывод определителя Якоби полярных координат 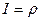 .
.
4. Вывод формул перехода к цилиндрическим координатам  .
.
5. Вывод определителя Якоби цилиндрических координат 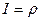 .
.
6. Вывод формул перехода к сферическим координатам:
 .
.
Лекция № 6
1. Доказать, что замена  сводит однородное уравнение к уравнению с разделяющимися переменными.
сводит однородное уравнение к уравнению с разделяющимися переменными.
2. Вывести общий вид решения линейного однородного уравнения.
3. Вывести общий вид решения линейного неоднородного уравнения методом Лагранжа.
4. Доказать, что замена  сводит уравнение Бернулли к линейному уравнению.
сводит уравнение Бернулли к линейному уравнению.
Лекция № 7.
1. Доказать, что замена 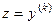 понижает на k порядок уравнения
понижает на k порядок уравнения  .
.
2. Доказать, что замена  понижает на единицу порядок уравнения
понижает на единицу порядок уравнения  .
.
3. Доказать теорему: Функция  является решением линейного однородного дифференциального уравнения
является решением линейного однородного дифференциального уравнения 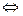
 есть характеристический корень.
есть характеристический корень.
4. Доказать теорему о том, что линейная комбинация решений линейного однородного дифф. уравнения тоже есть его решение.
5. Доказать теорему о наложении решений: Если  - решение линейного неоднородного дифф.уравнения с правой частью
- решение линейного неоднородного дифф.уравнения с правой частью  , а
, а  - решение такого же дифф.уравнения, но с правой частью
- решение такого же дифф.уравнения, но с правой частью  , то сумма
, то сумма  является решением уравнения с правой частью
является решением уравнения с правой частью  .
.
Лекция № 8.
1. Доказать теорему о том, что система функций линейно-зависима 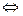
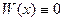 .
.
2. Доказать теорему о том, что существует n линейно-независимых решений линейного однородного дифференциального уравнения порядка n.
3. Доказать, что если 0 является корнем кратности  , то система решений, соответствующих этому корню, имеет вид
, то система решений, соответствующих этому корню, имеет вид  .
.
Лекция № 9.
1. Доказать с помощью показательной формы, что при умножении комплексных чисел модули умножаются, а аргументы складываются.
2. Доказать формулу Муавра для степени n
 .
.
3. Доказать формулу корня порядка n комплексного числа
 .
.
4. Доказать, что  и
и 
являются обобщениями синуса и косинуса, т.е. для действительных чисел по этим формулам получится синус (косинус).
5. Доказать формулу логарифма комплексного числа:
 .
.
Лекция № 10
1. Доказать, что сходимость ряда эквивалентна сходимости его остатка.
2. Доказать расходимость гармонического ряда 
3. Доказать на примере ряда  ,что закон коммутативности не выполняется в бесконечном случае.
,что закон коммутативности не выполняется в бесконечном случае.
4. Доказать необходимый признак сходимости.
5. Доказать интегральный признак Коши.
6. Доказать признак Даламбера в конечной форме.
7. Доказать признак Даламбера в предельной форме.
8. Доказать радикальный признак Коши в конечной форме.
Лекция № 11
1. Доказать признак Лейбница.
2. Доказать теорему Абеля. 1) Если ряд 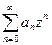 сходится в точке
сходится в точке  , то он сходится в любой точке
, то он сходится в любой точке 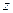 , для которой
, для которой 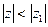 , причём абсолютно.
, причём абсолютно.
2) Если ряд 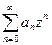 расходится в точке
расходится в точке  то он расходится в любой точке, для которой
то он расходится в любой точке, для которой  .
.
3. Доказать формулы радиуса сходимости степенного ряда.
 и
и 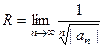 .
.
Лекция № 12.
Доказать теорему: Область сходимости ряда Лорана есть кольцо вида  .
.
Приложение 2.
Мелкие и устные вопросы на знание теории (для коллоквиумов).
Лекция № 1
1. Что такое первообразная и неопределённый интеграл, чем они отличаются?
2. Объяснить, почему 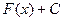 тоже является первообразной.
тоже является первообразной.
3. Напишите формулу интегрирования по частям.
4. Какая замена требуется в интеграле вида 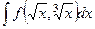 и каким образом она устраняет корни?
и каким образом она устраняет корни?
5. Запишите вид разложения подынтегральной рациональной дроби на простейшие в случае, когда все корни различны и действительны.
6. Запишите вид разложения подынтегральной рациональной дроби на простейшие в случае, когда все корни действительны, и есть один кратный корень кратности k.
Лекция № 2.
1. Напишите, какое разложение рациональной дроби на простейшие в случае, когда в знаменателе есть множитель 2 степени с отрицательным дискриминантом.
2. Какая замена сводит интеграл 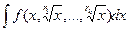 к рациональной дроби?
к рациональной дроби?
3. Что такие универсальная тригонометрическая подстановка?
4. Какие замены производятся в случаях, когда функция под знаком интеграла нечётна относительно синуса (косинуса)?
5. Какие замены производятся в случае наличия в подынтегральной функции выражений  ,
,  , или
, или 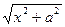 .
.
Лекция № 3.
1. Определение определённого интеграла.
2. Перечислите некоторые из основных свойств определённого интеграла.
3. Напишите формулу Ньютона-Лейбница.
4. Напишите формулу объёма тела вращения.
5. Напишите формулу длины явно заданной кривой.
6. Напишите формулу длины параметрически заданной кривой.
Лекция № 4.
1. Определение несобственного интеграла (с помощью предела).
2. Чем отличаются несобственные интегралы 1 и 2 рода.
3. Приведите простые примеры сходящихся интегралов 1 и 2 рода.
4. При каких 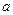 сходятся интегралы
сходятся интегралы 
 (Т1).
(Т1).
5. Как сходимость связана с конечным пределом первообразной (Т2)
6. Что такое необходимый признак сходимости, его формулировка.
7. Признак сравнения в конечной форме
8. Признак сравнения в предельной форме.
9. Определение кратного интеграла.
Лекция № 5.
1. Смена порядка интегрирования, показать на простейшем примере.
2. Напишите формулу площади поверхности.
3. Что такое полярные координаты, напишите формулы перехода.
4. Чему равен якобиан полярной системы координат?
5. Что такое цилиндрические и сферические координаты, в чём их отличие.
6. Чему равен якобиан цилиндрических (сферических) координат.
Лекция № 6.
1. Что такое дифференциальное уравнение 1 порядка (общий вид).
2. Что такое дифференциальное уравнение 1 порядка, разрешённое относительно производной. Приведите какой-нибудь пример.
3. Что такое уравнение с разделяющимися переменными.
4. Что такое общее, частное решение, условия Коши.
5. Что такое однородное уравнение, каков общий метод его решения.
6. Что такое линейное уравнение, в чём состоит алгоритм его решения, что такое метод Лагранжа.
7. Что такое уравнение Бернулли, алгоритм его решения.
Лекция № 7.
1. Какая замена необходима для уравнения вида  .
.
2. Какая замена необходима для уравнения вида  .
.
3. Покажите на примерах, как можно выразить  в виде
в виде  .
.
4. Что такое линейное дифференциальное уравнение порядка n.
5. Что такое характеристический многочлен, характеристическое уравнение.
6. Сформулировать теорему о том, при каком r функция  является решением линейного однородного дифференциального уравнения.
является решением линейного однородного дифференциального уравнения.
7. Сформулировать теорему о том, что линейная комбинация решений линейного однородного уравнения тоже есть его решение.
8. Сформулировать теорему о наложении решений и следствия из неё.
9. Что такое линейно-зависимая и линейно-независимая системы функций, привести какие-нибудь примеры.
10. Что такое определитель Вронского системы из n функций, приведите пример определителя Вронского для ЛЗС и ЛНС систем.
Лекция № 8.
1. Каким свойством обладает определитель Вронского, если система функция линейно-завимима.
2. Сколько существует линейно-независимых решений линейного однородного дифференциального уравнения порядка n.
3. Определение ФСР (фундаментальной системы решений) линейного однородного уравнения порядка n.
4. Сколько функций содержится в ФСР?
5. Запишите вид системы уравнений для нахождения  методом Лагранжа при n=2.
методом Лагранжа при n=2.
6. Запишите вид частного решения в случае, когда
 .
.
7. Что такое линейная система дифференциальных уравнений, напишите какой-нибудь пример.
8. Что такое автономная система дифференциальных уравнений.
9. Физический смысл системы дифференциальных уравнений.
10. Запишите, из каких функций состоит ФСР системы уравнений, если известны собственные числа и собственные векторы основной матрицы этой системы.
Лекция № 9.
1. Что такое мнимая единица.
2. Что такое сопряжённое число и что получится при его умножении на исходное.
3. Что такое тригонометрическая, показательная форма комплексного числа.
4. Напишите формулу Эйлера.
5. Что такое модуль, аргумент комплексного числа.
6. что происходит с модулями и аргументами при умножении (делении).
7. Напишите формулу Муавра для степени n.
8. Напишите формулу корня порядка n.
9. Напишите формулы обобщённых синуса и косинуса для комплексного аргумента.
10. Напишите формулу логарифма комплексного числа.
Лекция № 10
Что такое числовой ряд,его частичная сумма и остаток. Определение сходящегося ряда. Что такое абсолютная, условная сходимость.
Сформулировать необходимый признак сходимости.
Сформулировать интегральный признак Коши.
Сформулировать признак Даламбера в конечной форме.
Сформулировать признак Даламбера в предельной форме.
Сформулировать радикальный признак Коши в конечной форме.
Сформулировать радикальный признак Коши в предельной форме.
Лекция № 11
1. Сформулировать признак сравнения в конечной форме
2. Сформулировать признак сравнения в предельной форме
3. Сформулировать признак Лейбница
4. Определение области сходимости функционального ряда.
5. Запишите общий вид степенного ряда.
6. Сформулировать теорему Абеля об области сходимости степенного ряда.
7. Написать формулы радиуса сходимости степенного ряда.
Лекция № 12.
Запишите общий вид ряда Тейлора.
Как найти разложение в ряд Тейлора с помощью геометрической прогрессии.
Как решить дифференциальное уравнение с помощью степенного ряда.
Что такое ряд Лорана, главная, правильная часть.
Сформулировать теорему об области сходимостя ряда Лорана.
Приложение 3. Задачи из лекций.
Лекция № 1
Пример. 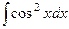 . Пример.
. Пример. 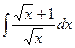 .
.
Пример.  . Пример.
. Пример. 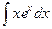 .
.
Пример.  Пример.
Пример.  .
.
Пример.  . Пример.
. Пример. 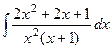 .
.
Лекция № 2
Пример.  . Пример.
. Пример.  .
.
Пример.  . Пример.
. Пример.  .
.
Пример.  . Пример.
. Пример.  .
.
Лекция № 3  ,
,  ,
,  ,
,  ,
,  .
.
Пример. Вычислить  .
.
Пример. Найти площадь фигуры, ограниченной линиями  .
.
Пример. Вывести формулу объёма шара  .
.
Лекция № 4
Вычислить  ,
,  ,
,  ,
, 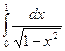 .
.
Выяснить сходимость:  ,
,  .
.
Вычислить 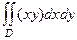 , где
, где  есть квадрат:
есть квадрат:  ,
,  .
.
Вычислить  , D треугольник с вершинами (0,0), (1,0), (1,1).
, D треугольник с вершинами (0,0), (1,0), (1,1).
Лекция № 5.
Пример. Сменить порядок интегрирования  .
.
Пример. Вычислить интеграл  где D куб
где D куб  .
.
Пример. Вычислить интеграл  где D - четверть круга единичного радиуса в первой четверти плоскости.
где D - четверть круга единичного радиуса в первой четверти плоскости.
Пример. Доказать формулу площади круга  с помощью полярных координат.
с помощью полярных координат.
Пример. С помощью сферических координат вывести формулу объёма шара 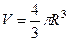 .
.
Лекция № 6.
Пример. Решить дифф. уравнение  .
.
Пример. Решить дифференциальное уравнение  .
.
Пример. Решить уравнение  .
.
Пример. Решить уравнение  .
.
Пример. Решить линейное уравнение  .
.
Лекция № 7.
Пример. Решить уравнение 2 порядка  .
.
Пример. Решить уравнение 3 порядка  .
.
Пример. Решить уравнение  .
.
Пример. Решить уравнение 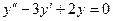 .
.
Пример. Решить уравнение  .
.
Лекция № 8.
Пример. Решить уравнение  методом Лагранжа (вариации произвольных постоянных).
методом Лагранжа (вариации произвольных постоянных).
Пример. Решить уравнение  методом неопределённых коэффициентов (по виду правой части).
методом неопределённых коэффициентов (по виду правой части).
Пример. Решить систему  с помощью сведения системы к одному уравнению.
с помощью сведения системы к одному уравнению.
Пример. Решить систему  с помощью собственных чисел и векторов.
с помощью собственных чисел и векторов.
Лекция № 9.
Пример. Умножить  .
.
Пример. Вычислить  .
.
Пример. Решить уравнение  , найти комплексные корни.
, найти комплексные корни.
Примеры. Записать в тригонометрической и показательной формах число  , число
, число  .
.
Пример. Поделить  в показательной форме.
в показательной форме.
Пример. Найти  по формуле Муавра.
по формуле Муавра.
Пример. Найдите все значения корня  .
.
Лекция № 10
Пример. Разложить в сумму действительной и мнимой части функцию:  .
.
Пример. Разложить в сумму действительной и мнимой части функцию:  .
.
Пример. Исследовать сходимость ряда  .
.
Пример. Исследовать сходимость ряда  .
.
Пример. Выяснить сходимость ряда  .
.
Лекция № 11. Пример. Выяснить сходимость  .
.
Пример. Выяснить, сходится ли ряд  .
.
Пример. Найти область сходимости ряда  .
.
Пример. Найти область сходимости ряда  .
.
Пример. Найти область сходимости ряда  .
.
Пример. Найти радиус и область сх. ряда  .
.
Пример. Найти сумму ряда 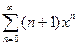 .
.
Пример. Найти сумму ряда 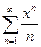 .
.
Лекция № 12.
Пример. Разложить 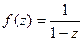 в степенной ряд (ряд Тейлора).
в степенной ряд (ряд Тейлора).
Пример. Разложить в ряд Тейлора с помощью геометрической прогрессии: 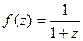 по степеням
по степеням 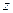 , то есть в круге с центром 0.
, то есть в круге с центром 0.
Пример. Разложить в ряд Тейлора с помощью геометрической прогрессии: 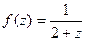 по степеням
по степеням 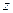 .
.
Пример. Разложить в ряд Тейлора с помощью геометрической прогрессии 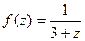 по степеням
по степеням 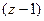 , то есть в круге с центром в точке 1.
, то есть в круге с центром в точке 1.
Пример. Найти  для
для  .
.
Пример.  решить с помощью степенных рядов.
решить с помощью степенных рядов.
Пример. Решить дифференциальное уравнение  с помощью степенных рядов.
с помощью степенных рядов.
Пример. Найти кольцо сх ряда Лорана  .
.



 и отсюда извлекается информация о значении
и отсюда извлекается информация о значении  , причём не требуется вычислять все производные включительно до n порядка, а сразу получаем значение n-й производной в точке. Ведь бывает так, что функция содержит произведение, и там число слагаемых удваивается на каждом шаге, и их уже 1024 для 10-й производной.
, причём не требуется вычислять все производные включительно до n порядка, а сразу получаем значение n-й производной в точке. Ведь бывает так, что функция содержит произведение, и там число слагаемых удваивается на каждом шаге, и их уже 1024 для 10-й производной. для
для  .
.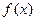 =
=  =
= 
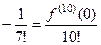

 .
. .
. с точностью
с точностью  .
. =
=  =
=  =
=  =
= очевидно, здесь 3 и последующие слагаемые заведомо меньше
очевидно, здесь 3 и последующие слагаемые заведомо меньше 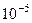 , и не повлияют на 4-й знак после запятой, поэтому приближённое значение
, и не повлияют на 4-й знак после запятой, поэтому приближённое значение =
= 

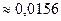 .
. в виде степенного ряда
в виде степенного ряда  и подставить его в дифференциальное уравнение, тогда решение найдётся тоже в виде ряда, т.е. можно знать строение решения, его график и т.д. даже без аналитического выражения этой функции..
и подставить его в дифференциальное уравнение, тогда решение найдётся тоже в виде ряда, т.е. можно знать строение решения, его график и т.д. даже без аналитического выражения этой функции.. решить с помощью степенных рядов.
решить с помощью степенных рядов.
 =
=  получаем:
получаем: ,
,  ,
,  и так далее.
и так далее. . А именно,
. А именно,  ,
, 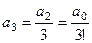 и т.д.
и т.д. здесь видно, что в скобках получилось разложение экспоненты. Итак,
здесь видно, что в скобках получилось разложение экспоненты. Итак, 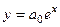 . Эту единственную константу можно переобозначить
. Эту единственную константу можно переобозначить  и получится знакомый из вид общего решения такого уравнения:
и получится знакомый из вид общего решения такого уравнения:  .
. с помощью степенных рядов.
с помощью степенных рядов.
 =
=  тогда:
тогда: ,
, 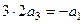 ,
, ,
,  ,
, ,
,  ,
, .
. ,
, 
 ,
,  ,...
,... ,
, 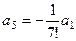 ,
, 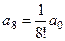 ,
,  ,...
,... =
= =
=  .
. и записать решение в привычном виде
и записать решение в привычном виде  .
. , то есть содержащий как положительные, так и отрицательные целые степени, называется рядом Лорана.
, то есть содержащий как положительные, так и отрицательные целые степени, называется рядом Лорана. правильная часть,
правильная часть,  главная часть, её также можно переписать в виде:
главная часть, её также можно переписать в виде: 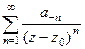 .
.
 .
. .
. . тогда для новой переменной
. тогда для новой переменной  ряд принимает такой вид:
ряд принимает такой вид:  . Это степенной ряд, его круг сходимости с центром в 0. То есть,
. Это степенной ряд, его круг сходимости с центром в 0. То есть, 
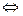

 , обозначим
, обозначим  , вот и получили
, вот и получили 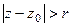 .
. : круг с выколотой точкой
: круг с выколотой точкой  .
.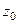 , а в любой точке из её окрестности - существует. Поэтому из области сходимости исключается лишь одна точка.
, а в любой точке из её окрестности - существует. Поэтому из области сходимости исключается лишь одна точка. : внешняя часть некоторого круга
: внешняя часть некоторого круга  .
. .
. получается
получается  , т.е.
, т.е. 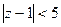

 получается
получается  , т.е.
, т.е.  .
. .
.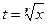 , где r = НОК (r1,...,rk) сводит интеграл
, где r = НОК (r1,...,rk) сводит интеграл 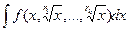 к интегралу от рациональной дроби.
к интегралу от рациональной дроби. сводит интеграл вида
сводит интеграл вида  к интегралу от рациональной дроби.
к интегралу от рациональной дроби.
 для универсальной тригонометрической замены
для универсальной тригонометрической замены  .
. сводит интеграл к рациональной дроби.
сводит интеграл к рациональной дроби.
 сводит интеграл к рациональной дроби.
сводит интеграл к рациональной дроби. замена
замена  своит интеграл к рациональной дроби.
своит интеграл к рациональной дроби.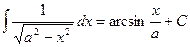
 замена
замена  своит интеграл к рациональной дроби.
своит интеграл к рациональной дроби. замена
замена  сводит интеграл к рациональной дроби.
сводит интеграл к рациональной дроби. является первообразной от функции
является первообразной от функции  .
.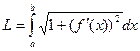 .
.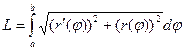
 сходится
сходится  ,
,  сходится
сходится  .
. .
. .
. .
. .
. .
. сводит однородное уравнение к уравнению с разделяющимися переменными.
сводит однородное уравнение к уравнению с разделяющимися переменными. сводит уравнение Бернулли к линейному уравнению.
сводит уравнение Бернулли к линейному уравнению.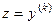 понижает на k порядок уравнения
понижает на k порядок уравнения  .
. понижает на единицу порядок уравнения
понижает на единицу порядок уравнения  .
. является решением линейного однородного дифференциального уравнения
является решением линейного однородного дифференциального уравнения  есть характеристический корень.
есть характеристический корень. - решение линейного неоднородного дифф.уравнения с правой частью
- решение линейного неоднородного дифф.уравнения с правой частью  , а
, а  - решение такого же дифф.уравнения, но с правой частью
- решение такого же дифф.уравнения, но с правой частью  , то сумма
, то сумма  является решением уравнения с правой частью
является решением уравнения с правой частью  .
. .
. , то система решений, соответствующих этому корню, имеет вид
, то система решений, соответствующих этому корню, имеет вид  .
. .
. .
. и
и 
 .
.
 ,что закон коммутативности не выполняется в бесконечном случае.
,что закон коммутативности не выполняется в бесконечном случае.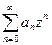 сходится в точке
сходится в точке  , то он сходится в любой точке
, то он сходится в любой точке 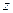 , для которой
, для которой 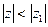 , причём абсолютно.
, причём абсолютно. .
. и
и 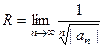 .
.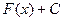 тоже является первообразной.
тоже является первообразной.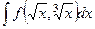 и каким образом она устраняет корни?
и каким образом она устраняет корни? ,
,  , или
, или 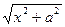 .
.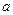 сходятся интегралы
сходятся интегралы  в виде
в виде  .
. является решением линейного однородного дифференциального уравнения.
является решением линейного однородного дифференциального уравнения. методом Лагранжа при n=2.
методом Лагранжа при n=2. .
.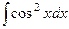 . Пример.
. Пример. 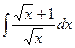 .
. . Пример.
. Пример. 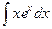 .
. Пример.
Пример.  .
. . Пример.
. Пример. 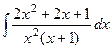 .
. . Пример.
. Пример.  .
. . Пример.
. Пример.  .
. . Пример.
. Пример.  .
. ,
,  ,
,  ,
,  ,
,  .
. .
. .
. .
. ,
,  ,
,  ,
, 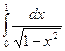 .
. ,
,  .
.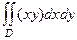 , где
, где  есть квадрат:
есть квадрат:  ,
,  .
. , D треугольник с вершинами (0,0), (1,0), (1,1).
, D треугольник с вершинами (0,0), (1,0), (1,1). .
. где D куб
где D куб  .
. где D - четверть круга единичного радиуса в первой четверти плоскости.
где D - четверть круга единичного радиуса в первой четверти плоскости. с помощью полярных координат.
с помощью полярных координат.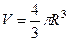 .
. .
. .
. .
. .
. .
. .
. .
.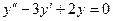 .
. .
. методом Лагранжа (вариации произвольных постоянных).
методом Лагранжа (вариации произвольных постоянных). с помощью сведения системы к одному уравнению.
с помощью сведения системы к одному уравнению. .
. .
. , найти комплексные корни.
, найти комплексные корни. , число
, число  .
. в показательной форме.
в показательной форме. по формуле Муавра.
по формуле Муавра. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.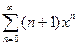 .
.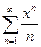 .
.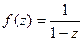 в степенной ряд (ряд Тейлора).
в степенной ряд (ряд Тейлора).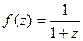 по степеням
по степеням 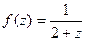 по степеням
по степеням 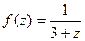 по степеням
по степеням 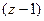 , то есть в круге с центром в точке 1.
, то есть в круге с центром в точке 1.


