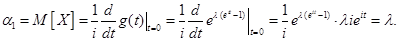Если  - ДСВ и
- ДСВ и  , где
, где 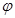 - неслучайная функция, то
- неслучайная функция, то  также ДСВ., причем её возможные значения
также ДСВ., причем её возможные значения  . Если при этом все
. Если при этом все  различны (функция
различны (функция  - строго монотонна), то
- строго монотонна), то  . Если же среди
. Если же среди  имеются одинаковые значения, то
имеются одинаковые значения, то


Если  - НСВ и
- НСВ и  , где
, где 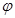 - монотонно возрастающая непрерывно дифференцируемая неслучайная функция, то
- монотонно возрастающая непрерывно дифференцируемая неслучайная функция, то  также НСВ., причем
также НСВ., причем

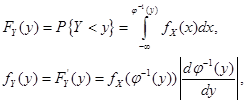 (4.21)
(4.21)
где  - обратная функция к
- обратная функция к 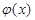 . Если же
. Если же 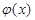 - немонотонная функция, то
- немонотонная функция, то
 (4.22)
(4.22)
где  означает
означает  - й интервал на оси
- й интервал на оси  , на котором
, на котором  . Плотность
. Плотность  получается дифференцированием
получается дифференцированием 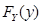 по
по 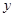 .
.
Пример. Пусть  . Найти закон распределения случайной величины
. Найти закон распределения случайной величины 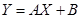 .
.
Решение.
 ;
; 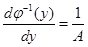 ;
;  ;
; 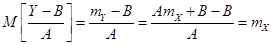
 .
.
Мы получили, что случайная величина  распределена по нормальному закону с параметрами
распределена по нормальному закону с параметрами  . Этот пример подтверждает известное свойство линейного преобразования гауссовских случайных величин – сохранение нормальности при линейных преобразованиях.
. Этот пример подтверждает известное свойство линейного преобразования гауссовских случайных величин – сохранение нормальности при линейных преобразованиях.
Задача композиции.
В одном из важных частных случаев функциональной зависимости  возникает задача определения закона распределения суммы компонент случайного вектора по известному закону совместного распределения его компонент. Если, например,
возникает задача определения закона распределения суммы компонент случайного вектора по известному закону совместного распределения его компонент. Если, например,  - НСВ с известной плотностью совместного распределения компонент
- НСВ с известной плотностью совместного распределения компонент  и
и  , то
, то
 (4.23)
(4.23)
Если  ДСВ, то закон распределения ДСВ
ДСВ, то закон распределения ДСВ  записывается в виде
записывается в виде

где суммирование распространяется на все значения индексов  и
и  , для которых выполняется условие
, для которых выполняется условие  .
.
В частности, если  - ДСВ с независимыми компонентами, то
- ДСВ с независимыми компонентами, то
 (4.24)
(4.24)
Если  - НСВ с независимыми компонентами, то формула (4.23) приводится к свертке двух плотностей:
- НСВ с независимыми компонентами, то формула (4.23) приводится к свертке двух плотностей:
 (4.25)
(4.25)
Задача определения закона распределения суммы независимых случайных величин носит название задачи композиции. Описанные выше формулы (4.24) и (4.25) дают непосредственное решение задачи композиции. Формулу (4.25) удобно применять в тех случаях, когда плотности распределения вероятностей компонент описываются одной формулой на всей оси (что, например, справедливо для нормального закона, закона Коши и т.д.). Другой подход к решению задачи композиции основан на применении свойств характеристической функции (см. ниже). Так как  , то, найдя
, то, найдя  , можно по характеристической функции восстановить закон распределения случайной величины Z.
, можно по характеристической функции восстановить закон распределения случайной величины Z.
Закон распределения W определенного вида называется композиционно устойчивым, если из того, что две независимые случайные величины X и У подчиняются закону распределения данного вида, следует, что их сумма X + Y подчиняются закону распределения W того же вида.
Пример. Доказать композиционную устойчивость нормального закона.
5. Характеристические функции случайных величин. Если  — комплекснозначная случайная величина, где X и Y — действительные случайные величины, то М [Z] = М [X] + i М [У].
— комплекснозначная случайная величина, где X и Y — действительные случайные величины, то М [Z] = М [X] + i М [У].
Характеристической функцией gx(t) случайной величины X называется комплекснозначная неслучайная функция действительного аргумента t определяемая равенством
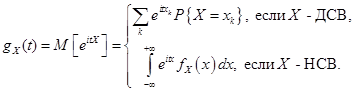
Для НСВ характеристическая функция представляет собой преобразование Фурье от плотности распределения. Поэтому плотность выражается как обратное преобразование Фурье от характеристической функции

Свойства характеристической функции
-

- Если
 - характеристическая функция случайной величины
- характеристическая функция случайной величины  и
и  то
то

-
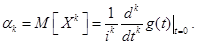
- Если случайные величины
 независимы, а
независимы, а  , то
, то

Характеристической функцией случайного вектора  называется комплекснозначная неслучайная функция
называется комплекснозначная неслучайная функция  действительных переменных
действительных переменных  :
:

Пример. Найти числовые характеристики  случайной величины
случайной величины  , распределённой по закону Пуассона, используя характеристическую функцию.
, распределённой по закону Пуассона, используя характеристическую функцию.

По свойству 3 находим
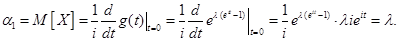
Дисперсию находим по формуле 

Окончательно находим

Литература
1. Статистическая динамика и оптимизация управления летательных аппаратов: Учебн. пособие для авиационных специальностей вузов/ А, А. Лебедев, В. Т. Бобронников, М. Н. Красильщиков, В. В. Малышев. – М. Машиностроение, 1985.
2. Вентцель Е. С. Теория вероятностей. – М.: Высшая школа, 1999.
3. Кибзун А. И., Горяинова Е. Р., Наумов А. В., Сиротин А. Н. Теория вероятностей и математическая статистика. – М.: ФИЗМАТЛИТ, 2002.
4. Сборник задач по математике для втузов. Часть 4: /Под общей ред. А. В. Ефимова и А. С. Поспелова. – М.: Изд-во ФИЗМАТЛИТ, 2003.



 - ДСВ и
- ДСВ и  , где
, где 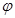 - неслучайная функция, то
- неслучайная функция, то  также ДСВ., причем её возможные значения
также ДСВ., причем её возможные значения  . Если при этом все
. Если при этом все  различны (функция
различны (функция  - строго монотонна), то
- строго монотонна), то  . Если же среди
. Если же среди 

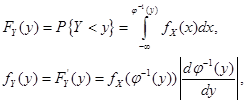 (4.21)
(4.21) - обратная функция к
- обратная функция к 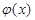 . Если же
. Если же  (4.22)
(4.22) означает
означает  - й интервал на оси
- й интервал на оси  , на котором
, на котором  . Плотность
. Плотность  получается дифференцированием
получается дифференцированием 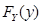 по
по 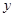 .
. . Найти закон распределения случайной величины
. Найти закон распределения случайной величины 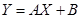 .
. ;
; 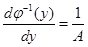 ;
;  ;
; 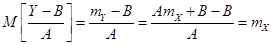
 .
. . Этот пример подтверждает известное свойство линейного преобразования гауссовских случайных величин – сохранение нормальности при линейных преобразованиях.
. Этот пример подтверждает известное свойство линейного преобразования гауссовских случайных величин – сохранение нормальности при линейных преобразованиях. возникает задача определения закона распределения суммы компонент случайного вектора по известному закону совместного распределения его компонент. Если, например,
возникает задача определения закона распределения суммы компонент случайного вектора по известному закону совместного распределения его компонент. Если, например,  - НСВ с известной плотностью совместного распределения компонент
- НСВ с известной плотностью совместного распределения компонент  и
и  , то
, то (4.23)
(4.23)
 , для которых выполняется условие
, для которых выполняется условие  .
. (4.24)
(4.24) (4.25)
(4.25) , то, найдя
, то, найдя  , можно по характеристической функции восстановить закон распределения случайной величины Z.
, можно по характеристической функции восстановить закон распределения случайной величины Z. — комплекснозначная случайная величина, где X и Y — действительные случайные величины, то М [Z] = М [X] + i М [У].
— комплекснозначная случайная величина, где X и Y — действительные случайные величины, то М [Z] = М [X] + i М [У].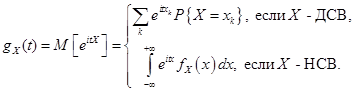


 - характеристическая функция случайной величины
- характеристическая функция случайной величины  то
то
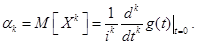
 независимы, а
независимы, а  , то
, то
 называется комплекснозначная неслучайная функция
называется комплекснозначная неслучайная функция  действительных переменных
действительных переменных  :
:
 случайной величины
случайной величины  , распределённой по закону Пуассона, используя характеристическую функцию.
, распределённой по закону Пуассона, используя характеристическую функцию.