Особенность измерения и оценивания качества сложных систем проявляется в том, что для разных частных показателей одной и той же системы могут применяться разные типы шкал.
Кроме того, для уточнения значений могут проводиться несколько измерений каждого из показателей. В этом случае, как уже говорилось, обобщенный показатель системы представляет собой осредненную величину частных показателей. При работе с величинами, измеренными в разных шкалах, для исключения грубых ошибок при оценке системы следует помнить основные правила и допустимые операции осреднения показателей.
1. Процедура осреднения допускается только для различных измерений одного и того же показателя или для нескольких однородных показателей, если измерения проведены с использованием одной шкалы.
2. Каждое значение показателя  при оценке может иметь различную ценность, которую учитывают с помощью весовых коэффициентов
при оценке может иметь различную ценность, которую учитывают с помощью весовых коэффициентов  :
:
 .
.
3. Для получения осредненного значения показателя наиболее часто используют следующие формулы осреднения:
· средневзвешенное арифметическое (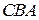 ):
):
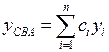 ,
,
· среднеарифметическое ( ):
):
 ,
,
· среднеквадратичное ( ):
):
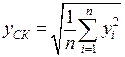 ,
,
· средневзвешенное геометрическое (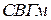 ):
):
 ,
,
· среднегеометрическое ( ):
):
 ,
,
· средневзвешенное гармоническое ( ):
):
 ,
,
· среднегармоническое ( ):
):
 .
.
Соотношение между данными типами средних величин определяется правилом мажорантности средних  . Простые и взвешенные средние величины различаются как по способу вычисления, так и по роли в решении задач системного анализа: средневзвешенные величины применяют при сравнении систем с учетом вклада различных факторов в осредненную оценку.
. Простые и взвешенные средние величины различаются как по способу вычисления, так и по роли в решении задач системного анализа: средневзвешенные величины применяют при сравнении систем с учетом вклада различных факторов в осредненную оценку.
Среднеарифметическое значение используют для сравнения абсолютных значений какого-либо параметра нескольких систем (или одной системы при нескольких измерениях).
Среднеквадратичные значения используют для определения вариации параметра системы в совокупности (среднеквадратичного отклонения).
Среднегеометрические значения параметра системы используют в тех случаях, когда среднее значение качественно одинаково удалено от максимального и минимального значений, в результате чего становятся важными не абсолютные значения, а их относительный разброс.
Среднегармонические значения параметров используют в тех случаях, когда для определения критерия оценки используются суммарные значения величин, обратных индивидуальным значениям параметров системы.
Вопрос о применении средних в настоящее время исследован достаточно полно. Связывая его со шкалами измерений, можно сделать следующие выводы:
· для величин, измеренных в номинальной шкале, никакие осреднения недопустимы;
· среднеарифметическое осреднение может быть применено для величин, измеренных в шкалах интервалов, разностей, отношений и абсолютной, но недопустимо для шкал порядка;
· в качестве основной оценки среднего для шкал порядка, интервалов, разностей, отношений и абсолютной рекомендуется медиана;
· математическое ожидание допустимо для шкал интервалов, разностей, отношений и абсолютных (применение для величин, измеренных в шкале порядка, некорректно);
· среднегеометрическое осреднение является единственно допустимым для степенных и логарифмических шкал;
· для шкал отношений также допустимы средневзвешенное арифметическое, среднегармоническое и среднеквадратичное осреднения измеренных величин.





 при оценке может иметь различную ценность, которую учитывают с помощью весовых коэффициентов
при оценке может иметь различную ценность, которую учитывают с помощью весовых коэффициентов  :
: .
.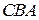 ):
):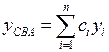 ,
, ):
): ,
, ):
):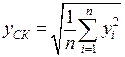 ,
, ):
): ,
, ):
): ,
, ):
): ,
, ):
): .
. . Простые и взвешенные средние величины различаются как по способу вычисления, так и по роли в решении задач системного анализа: средневзвешенные величины применяют при сравнении систем с учетом вклада различных факторов в осредненную оценку.
. Простые и взвешенные средние величины различаются как по способу вычисления, так и по роли в решении задач системного анализа: средневзвешенные величины применяют при сравнении систем с учетом вклада различных факторов в осредненную оценку.


