Электрические поля, которые создаются неподвижными электрическими зарядами, называются электростатическими.

Потенциал электростатического поля. Принцип суперпозиции для потенциала.

Для электростатического поля справедлива теорема о циркуляции: Циркуляция вектора напряженности электростатического поля равна нулю:

.

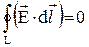Это соотношение, выражающее потенциальный характер электростатического поля, справедливо как в вакууме, так и в веществе. Отсюда следует, что заряд в электростатическом поле обладает потенциальной энергией.

Энергетической характеристикой электростатического поля служит его потенциал.

Потенциалом электростатического поля называется скалярная физическая величина j, равная потенциальной энергииW_рположительного единичного точечного заряда, помещённого в рассматриваемую точку поля:

.

Потенциал поля точечного заряда q_i в вакууме:

.

Принцип суперпозиции для потенциала:

j= ,

т. е. при наложении электростатических полей их потенциалы складываются алгебраически.

Связь между напряженностью поля и потенциалом (интегральная и дифференциальная).

Элементарная работа, совершенная при бесконечно малом перемещении заряда qв электрическом поле

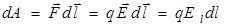и dA = – dU = – d (qφ). Так как q = const, а 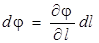, то

(6.9)

где E_l – проекция вектора на произвольное направление. В соответствии с формулой (6.9)

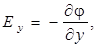
а

(6.10)

Напряженность в какой-либо точке электростатического поля равна градиенту потенциала в этой точке, взятому с обратным знаком.

Полярные и неполярные диэлектрики.

Метод изображений.

 

Метод изображений основан на подгонке потенциала под граничные условия: необходимо найти другую задачу (конфигурацию зарядов), у которой конфигурация поля в интересующей нас части пространства была бы той же. Рассмотрим точечный заряд , когда он находится около безграничной проводящей плоскости (рис. 1,а).

В нашем случае другой задачей является задача с двумя зарядами и (рис.1,б), поле этой системы известно. Совместим со средней эквипотенциальной поверхностью проводящую плоскость и уберем заряд . Согласно теореме единственности поле в верхнем полупространстве останется прежним (рис. 1,в). Для вычисления этого поля достаточно ввести фиктивный заряд – изображение 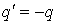, противоположный по знаку заряду , поместив его на другую сторону проводящей плоскости на таком же расстоянии от нее, что и заряд . Фиктивный заряд 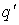создает в верхнем полупространстве точно такое же поле, как и индуцированные заряды на плоскости.

 

Конденсаторы

Если двум изолированным друг от друга проводникам сообщить заряды q₁и q₂, то между ними возникает некоторая разность потенциалов Δφ, зависящая от величин зарядов и геометрии проводников. Разность потенциалов Δφ между двумя точками в электрическом поле часто называют напряжением и обозначают буквой U. Наибольший практический интерес представляет случай, когда заряды проводников одинаковы по модулю и противоположны по знаку: q₁= – q₂= q. В этом случае можно ввести понятие электрической емкости.

Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:

В системе СИ единица электроемкости называется фарад (Ф):

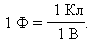
Бывают нужны такие устройства, которые при небольшом потенциале накапливали бы на себе большие заряды. В основу таких устройств, называемых конденсаторами, положен тот факт, что ёмкость проводника возрастает при приближении к нему другого проводника. Это вызвано тем, что под действием поля, создаваемого заряженным проводником, на находящемся поблизости незаряженном проводящем теле возникают индуцированные заряды. Конденсаторы делают в виде двух проводников, называемых обкладками, помещенных близко друг к другу. Для того, чтобы внешние тела не влияли на ёмкость конденсатора, обкладкам предают такую форму и так располагают их друг относительно друга, чтобы поле, создаваемое накапливаемыми на них зарядами, было сосредоточено внутри конденсатора.

Каждая из заряженных пластин плоского конденсатора создает вблизи поверхности электрическое поле, модуль напряженности которого выражается соотношением

Согласно принципу суперпозиции, напряженность поля, создаваемого обеими пластинами, равна сумме напряженностей и 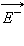полей каждой из пластин:

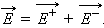
Внутри конденсатора вектора и 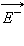параллельны; поэтому модуль напряженности суммарного поля равен

Вне пластин вектора и 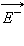направлены в разные стороны, и поэтомуE = 0. Поверхностная плотность σ заряда пластин равна q / S, где q – заряд, а S – площадь каждой пластины. Разность потенциалов Δφ между пластинами в однородном электрическом поле равна Ed, где d – расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора:

Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз:

Примерами конденсаторов с другой конфигурацией обкладок могут служить сферический и цилиндрический конденсаторы. Сферический конденсатор – это система из двух концентрических проводящих сфер радиусов R₁ и R₂. Цилиндрический конденсатор – система из двух соосных проводящих цилиндров радиусов R₁ и R₂ и длины L. Емкости этих конденсаторов, заполненных диэлектриком с диэлектрической проницаемостью ε, выражаются формулами:

(сферический конденсатор), (цилиндрический конденсатор).

 

Закон Ома

для однородного участка цепи имеет вид:

где 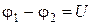– разность потенциалов (напряжение) на концах участка; 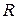– сопротивление.

Для неоднородного участка цепи этот закон записывается так:

 

 

 

где – ЭДС источника тока на этом участке; – внутреннее сопротивление источника;

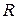– внешнее сопротивление цепи; 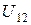– падение напряжения на участке 1-2.

· Для замкнутой цепи .

4. Сопротивление цилиндрического однородного проводника равно ,

где – удельное сопротивление; – удельная проводимость;

– длина; S – площадь поперечного сечения проводника.

Вектор магнитной индукции.

Вектор магнитной индукции - аналог напряженности электрического поля. Основной силовой характеристикой маг­нитного поля является вектор магнитной индукции. Вектор индукции магнитного поля B⃗направлен от южного полюса S стрелки (свободно вращающейся в магнитном поле) к северному N

Закон Ампера.

Закон Ампера - сила, действующая на проводник с током, помещенный в однородное магнитное поле, пропорциональна длине проводника, вектору магнитной индукции, силе тока и синусу угла между вектором магнитной индукции и проводником. Если размер проводника произволен, а поле неоднородно, то формула выглядит следующим образом: Направление силы Ампера определяется по правилу левой руки.Магнитный момент витка с током – физическая величина характеризующий магнитные свойства системы в виде кругового витка с током Где, I ток протекающий по витку S площадь витка с током n нормаль к плоскости в которой находится виток

 

Энергия контура с током.

Энергия контура с током. - Контур с током, помещенный в магнитное поле, обладает запасом энергии. Действительно, чтобы повернуть контур с током на некоторый угол в направлении, обратном направлению его поворота в магнитном поле, необходимо совершить работу против сил, действующих на этот контур со стороны поля. По величине эта работа равна: . Совершенная над контуром работа идет на увеличение его энергии. Поворачиваясь в первоначальное положение, контур возвратит затраченную на его поворот работу, совершив ее над какими-либо телами. Следовательно, запасенная контуром энергия есть:

24) Механические колебания под действием упругой силы…

 

Механические колебания под действием упругой силы.

Уравнение гармонических колебаний - x = x _m cos (ω t + φ₀)

Амплитудаx = Xm*cos(ω0*t).

Частота

период и фаза колебаний- Период свободных колебаний:

T = 2*pi/ ω0 = 2*pi*√(m/k), период свободных колебаний для математического маятника

T = 2*pi*√(l/g),Фаза -φ = ω t + φ₀

начальная фаза.φ₀при t = 0 φ = φ₀

Колебания координаты и скорости груза, закрепленного на упругой пружине.

Электромагнитные колебания.

Электромагнитные колебания - периодические изменения напряжённости E и индукции В.

колебательный контур - это электрическая цепь, содержащая индуктивность L, емкость С и сопротивление R, в которой могут возбуждаться электрические колебания гармонические колебания в контуре - q = q_m cos ω₀t,

i = q' = - ω₀ q_m sin ω₀ t = I_m cos (ω₀t + π/2),

 

где q_m — амплитуда колебаний заряда, I_m = ω₀ q_m — амплитуда колебаний силы тока. Колебания силы тока опережают по фазе на π/2 колебания заряда.

 

Уравнение гармонических колебаний,

амплитуда,

частота,

период и фаза колебаний – период - 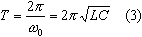фаза - φ = ώt + φ₀

начальная фаза.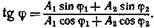

Колебания заряда и тока в колебательном контуре.

 

Электромагнитные колебания.

Электромагнитные колебания - периодические изменения напряжённости E и индукции В

колебательный контур - это электрическая цепь, содержащая индуктивность L, емкость С и сопротивление R, в которой могут возбуждаться электрические колебания гармонические колебания в контуре - q = q_m cos ω₀t,

i = q' = - ω₀ q_m sin ω₀ t = I_m cos (ω₀t + π/2),

 

гармонические колебания в контуре.

Электрические поля, которые создаются неподвижными электрическими зарядами, называются электростатическими.

Силовой характеристикой электростатического поля является его напряженность.

Напряженность электростатического поля в данной точке есть физическая величина, определяемая силой – F, действующей на пробный единичный положительный заряд – Q,, помещенный в эту точку поля:

 

Направление вектора совпадает с направлением силы, действующей на положитель­ный заряд.

Единица напряженности электростатического поля — «Ньютон на Кулон» (Н/Кл).

Н/Кл— напряженность такого поля, которое на точечный заряд1Клдействует с силой в1Н;1 Н/Кл = 1В/м, гдеВ(вольт) — единица потенциала электростатического поля.

2) Принцип суперпозиции (наложения) полей формулируется так:

Если в данной точке пространства различные заряженные частицы создают электрические поля, напряженности которых 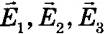и т. д., то результирующая напряженность поля в этой точке равна: .

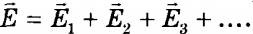Принцип суперпозиции полей справедлив для случая, когда поля, созданные несколькими различными зарядами, не оказывают никакого влияния друг на друга, т. е. ведут себя так, как будто других полей нет. Опыт показывает, что для полей обычных интенсивностей, встречающихся в природе, это имеет место в действительности.

Благодаря принципу суперпозиции для нахождения напряженности поля системы заряженных частиц в любой точке достаточно воспользоваться выражением напряженности поля точечного заряда.

 

 

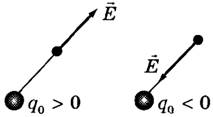
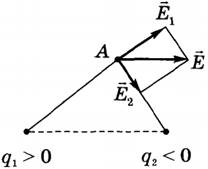
На рисунке ниже показано, как в точке A определяется напряженность поля , созданная двумя точечными зарядами q₁ и q₂.

 

 

Силовые линии электрического поля.

Электрическое поле в пространстве принято представлять силовыми линиями. Понятие о силовых линиях ввел М. Фарадей при исследовании магнетизма. Затем это понятие было развито Дж. Максвеллом в исследованиях по электромагнетизму.

Силовая линия, или линия напряженности электрического поля, — это линия, касательная к которой и каждой ее точке совпадает с направлением силы, действующей на положительный точечный заряд, находящийся в этой точке поля.

На рисунках ниже изображены линии напряженности положительно заряженного шарика (рис. 1); двух разноименно заряженных шариков (рис. 2); двух одноименно заряженных ша­риков (рис. 3) и двух пластин, заряженных разными по знаку, но одинаковыми по абсолютной величине зарядами (рис. 4).

 

 

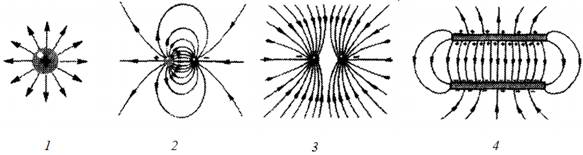
Линии напряженности на последнем рисунке почти параллельны в пространстве между пластинами, и плотность их одинакова. Это говорит о том, что поле в этой области пространства однородно. Однородным называется электрическое поле, напряженность которого одинакова во всех точках пространства.

В электростатическом поле силовые линии не замкнуты, они всегда начинаются на положительных зарядах и заканчиваются на отрицательных зарядах. Они нигде не пересекаются, пересечение силовых линий говорило бы о неопределенности направления напряженности поля в точке пересечения. Плотность силовых линий больше вблизи заряженных тел, где напряженность поля больше.

 

Поле заряженного шара.

Напряженность поля заряженного проводящего шара на расстоянии от центра шара, превышающем его радиус r ≥ R. определяется по той же формуле, что и поля точечного заряда . Об этом свидетельствует распределение силовых линий (рис. а), аналогичное распределению линий напряженности точечного заряда (рис. б).

 

 

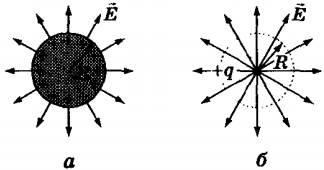
Заряд шара распределен равномерно по его поверхности. Внутри проводящего шара напряженность поля равна нулю.