Допишите формулу дисперсии дискретной случайной величин

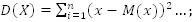
A. xi

B. mi

+C. pi

D. f(x)

118. Определите верное равенство:

A

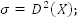
+ B

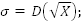
C

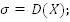
D

Какая характеристика характеризует положение случайной величины?

A. M(X)

B. D(X)

+ C

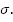
Какая характеристика переводит единицы измерения?

A. M(X)

+ B. D(X)

C.

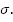
121. Дискретная случайная величина задана законом распределения: Xi -1 0 1 2 pi 0,1 0,3 0,5 0,1. Математическое ожидание величины X составит:

A. 0,3

B. 0,4

+C. 0,6

122. Дискретная случайная величина X задана таблицей: Xi 0 1 2 pi 0,3 0,5 0,2. математическое ожидание случайной величины равно…

A. 1,3

+ B. 0,9

C. 1,2

123. Дискретная случайная величина X задана таблицей: Xi 0 1 2 pi 0,3 0,5 0,2. среднее квадратическое отклонение случайной величины X равно:

A. 0,909

+ B. 0,7

C. 0,64

124. Дискретная случайная величина X задана таблицей: Xi -1 0 1 pi 0,4 0,5 0,1 математическое ожидание случайной величины равно…

A. -0,5

+ B. -0,3

C. 0

125. Дискретная случайная величина X задана таблицей: Xi -1 0 1 pi 0,4 0,5 0,1 среднее квадратическое отклонение случайной величины X равно:

A. 0,46

+ B. 0,64

C. 0,53

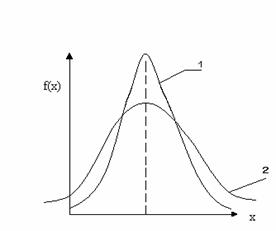
126. Для двух кривых НРСВ сравните величины σ

А

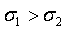
В

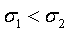
Непрерывная случайная величина Х задана плотностью распределения вероятностей. Тогда математическое ожидание этой нормально распределенной случайной величины равно

А. 3

В. 18

С. 4

НРСВ Х задана плотностью распределения:f(x). Математическое ожидание m и дисперсия D этой СВ равны

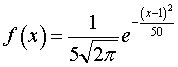
А. m=1, D=25

В. m=5, D=1

С. m=5, D=25

129. Правило трех сигм означает, что:

+ А. Вероятность попадания СВ в интервал, то есть близка к единице

В. НРСВ не может выйти за пределы

С. График плотности НРСВ симметричен относительно математического ожидания

130. СВ Х распределена нормально с математическим ожиданием, равным 5 и СКО, равным 2 единицы. Выражение для плотности распределения этой НРСВ имеет вид:

А

В

С

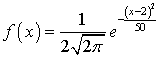
131. НРСВ Х имеет математическое ожидание a=10 и СКО =5. С вероятностью 0,9973 величина Х попадет в интервал:

А. (5; 15)

В. (0; 20)

С. (-5; 25)

Для стандартизованного нормального распределения величина равна

+ А. 1

В. 2

С. пи/2

133. Эмпирическое нормальное распределение образуется в том случае, когда:

+ А. действует большое число независимых случайных причин, имеющих примерно одинаковый статистический вес;

В. действует большое число сильно зависимых между собой случайных величин;

С. объем выборки небольшой.

134. Непрерывная случайная величина, возможные значения которой лежат в некоторых конечных пределах, распределена по закону равномерной плотности, если:

А. плотность вероятности постоянна;

+ В. все значения случайной величины имеют одинаковую вероятность;

С. плотность вероятности будет неотрицательной величиной и интеграл от плотности по отрезку, в котором заключены все значения случайной величины, равен единице.

135. Укажите формулу плотности вероятности нормально распределенной непрерывной случайной – формулу Гаусса:

А

В

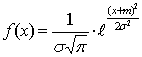
+ С

136. Случайная величина Х распределена нормально m(x) = 12, σ(x) =3. Укажите функцию плотности распределения величины Х:

A

B

+ C

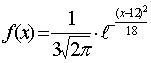
D

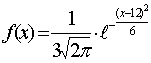
Вероятность любого отдельного значения дискретной случайной величины равна

A. 0;

B. 1;

+ C. от 0 до 1 включительно;

D. близка к 0.