Основные приемы и методы решения логических задач

Основные приемы и методы решения логических задач

 

Многие логические задачи решаются рассуждением,

Идея метода состоит в том, что мы проводим рассуждения, используя последовательно все условия задачи, анализируя каждую из воз­можных ситуаций. Отбрасывая неподходящие, мы

Приходим к выводу, который и будет являться ответом задачи.

Рассмотрим этот способ на примерах.

Задача 1.

Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский.

На вопрос, какой язык изучает каждый из них, один ответил: "Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский".

Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны.

Какой язык изучает каждый из молодых людей?

Решение.

Имеется три утверждения. Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки.

Это противоречит условию задачи, поэтому первое утверждение ложно.

Если верно второе утверждение, то первое и третье должны быть ложны.

При этом получается, что никто не изучает китайский.

Это противоречит условию, поэтому второе утверждение тоже ложно.

Остается считать верным третье утверждение, а первое и второе — ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей.

Ответ: Сергей изучает китайский язык,

Михаил — японский,

Вадим — арабский.

Задача 2.

Три гадалки-близнецы сидели рядом.

Одну звали Правда (всегда говорила только правду),

вторую звали Шутница (иногда говорила правду, иногда - ложь), а третью звали Ложь (всегда говорила только ложь).

Философ решил выяснить, кто из них кто. Он задал три вопроса:

"Кто сидит рядом с тобой?" - спросил он крайнюю слева и получил ответ: "Правда".

"Кто ты?" - спросил он среднюю и услышал: "Я - Шутница".

"Кто сидит рядом с тобой?" - спросил он крайнюю справа и услышал: "Ложь".

Кто сидел крайней слева?

Решение.

Если бы самая первая гадалка была бы Правдой, она бы не сказала, что рядом с ней сидит Правда.

По той же причине вторая из опрошенный гадалок тоже не является Правдой.

Остается, что сидящая справа, третья гадалка - Правда.

Ей можно верить. А она сказала, что посередине сидит Ложь.

Следовательно, первая в ряду гадалок - Шутница.

Ответ - Шутница;

 

Задача 3.

На конкурсе, капитанов КВН проверяли на со­образительность.

Трое испытуемых капитанов садятся друг другу в затылок. (Понятно, что сидящий сзади видит головы двух впереди сидящих товарищей, а сидящий вторым видит голову только одного впереди сидящего. Оборачиваться им запре­щено.

Ведущий показывает испытуемым, что у него имеется пять колпаков: три черных и два белых. Затем он каждому надевает на голову колпак неизвестного для испытуемого цвета, а оставшиеся колпаки прячет.

Испытуемым предлагается в течение короткого времени назвать цвет своего колпака.

Докажите, что каким бы образом ни были рас­пределены цвета колпаков, среди испытуемых найдется по край­ней мере один, который может совершенно уверенно назвать цвет своего колпака.

 

Решение. Рассмотрим все случаи:

 

1 случай. Первым двум капитанам будут надеты белые колпаки. Так как их только два и сидящий сзади видит их надетыми на головы впереди сидящих, то он определенно скажет, что у него на голове черный колпак. (Безусловно, что после такого заявления сзади сидящего каждый из впереди сидящих может сказать, что у него на голове белый колпак).

 

2 случай. Наденем на голову первому капитану белый колпак, а второму — черный. Теперь сидящий сзади не может знать, какого цвета колпак у него на голове, поскольку он может быть либо белым, либо черным.

В этом случае сидящий вто­рым рассуждает так: «Я вижу белый колпак. Если бы и на мне был белый колпак, то сидящий сзади уже заявил бы, что на нем черный колпак. Но он молчит. Значит, он не ви­дит на мне белого колпака. Следовательно, на мне черный колпак».

Таким образом, в этом случае второй капитан может вполне определенно заявить, что на нем черный колпак. (После такого заявления и впереди сидящий может сказать определенно, что на нем белый колпак. Сидящий же сзади назвать цвет своего колпака не может).

 

3 случай. Наденем теперь впереди сидящему капитану черный колпак, а второму и третьему — безразлично какой. В этом случае ни третий, ни второй не могут назвать цвет своего колпака.

Сидящий первым будет рассуждать так: «Если бы на мне был белый колпак, то кто-нибудь из сзади сидящих знал бы цвет своего колпака и сказал бы об этом. Но они оба молчат. Значит, на мне нет белого колпака». В этом слу­чае впереди сидящий может определенно заявить, что на нем черный колпак.

 

Метод второй: Метод таблиц

Идея метода:

Задача 1.

Три клоуна Бим, Бам и Бом вышли на арену в красной, зеленой и синей рубашках. Их туфли были тех же цветов. У Бима цвета рубашки и туфель совпадали. У Бома ни туфли, ни рубашка не были красными. Бам был в зеленых туфлях, а в рубашке другого цвета. Как были одеты клоуны?

 

Решение.

Составим таблицу, в столбцах которой отметим возможные цвета рубашек и туфель клоунов (буквами К, З и С обозначены красный, зеленый и синий цвета).

Будем заполнять таблицу, используя условия задачи. Туфли Бама зеленые, а рубашка не является зеленой. Ставим знак + в клетку 2-й строки и 5-го столбца, и знак - в клетку 2-й строки и 2-го столбца. 7

Следовательно, у Бима и Бома туфли уже не могут быть зелеными, так же как не могут быть туфли Бама синими или красными. Отметим все это в таблице (см. табл. 1).

 

 

Далее, туфли и рубашка Бома не являются красными, отметим соответствующие ячейки таблицы знаком –. Из таблицы, заполненной на этом этапе, видим, что красные туфли могут быть только у Бима, а, следовательно, туфли Бома - синие. Правая часть таблицы заполнена, мы установили цвета обуви клоунов (табл.1).

Цвет рубашки Бима совпадает с цветом его туфель и является красным. Теперь легко устанавливается владелец зеленой рубашки - Бом. Бам, в таком случае, одет в рубашку синего цвета.

 

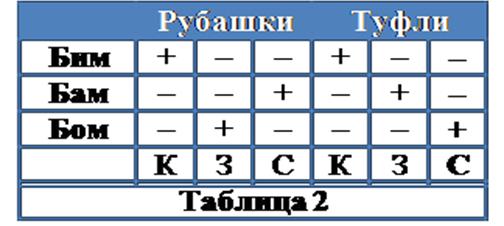
Мы полностью заполнили таблицу, в которой однозначно устанавли-ваются цвета туфель и рубашек клоунов (см. табл. 2):

Бим одет в красную рубашку и красные туфли, Бам в синей рубашке и зеленых туфлях,

Бом в зеленой рубашке и туфлях синего цвета.

Ответ:

Бим одет в красную рубашку и красные туфли,

Бам в синей рубашке и зеленых туфлях, Бом в зеленой рубашке и туфлях синего цвета.

 

Задача 2.

В оркестр приняли на работу трёх музыкантов: Борисова, Сомова и Васильева, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе.

Известно, что:

1) Сомов самый высокий

2) играющий на скрипке меньше ростом играющего на флейте;

3) играющие на скрипке и флейте и Борисов любят пиццу;

4) когда между альтистом и трубачом возникает ссора,

Сомов мирит их;
5) Борисов не умеет играть ни на трубе, ни на гобое.

На каких инструментах играет каждый из музыкантов,

если каждый владеет двумя инструментами?

 

Решение.

а) Составим таблицу, заполняя клетки числами 0 и 1 в зависимости от того ложно или истинно высказывание.

Музыкантов трое, инструментов шесть.

Значит, каждый музыкант играет на двух инструментах, которыми остальные не владеют.

Из условия 4 следует, что Сомов не умеет играть ни на альте, ни на трубе.

Из условий 3 и 5 следует, что Борисов не умеет играть на скрипке, флейте, трубе и гобое.

Следовательно, инструменты Борисова – альт и кларнет.

	скрипка	флейта	альт	кларнет	гобой	труба
Борисов
Сомов
Васильев

 

Из таблицы следует, что на трубе может играть только Васильев.

Из условий 1 и 2 следует, что Сомов не скрипач.

Так как на скрипке не играет ни Борисов, ни Сомов, то скрипачом является Васильев.

 

	скрипка	флейта	альт	кларнет	гобой	труба
Борисов
Сомов
Васильев

 

Из таблицы видно, что только Сомов может играть на флейте и гобое.

	скрипка	флейта	альт	кларнет	гобой	труба
Борисов
Сомов
Васильев

Ответ.

Борисов играет на альте и кларнете, Сомов – на флейте и гобое,

Васильев – на скрипке и трубе.

 

 

Метод графов

Задача 1. Любители музыки

В клубе «Отдых» познакомились 3 любителя клубной музыки видов техно, хаус, рейв. Один говорит: «Вы какую музыку больше любите? Я техно люблю!». Другой ответил, что любит хаус, а третий сказал, что не любит ни техно, ни хаус, но зато обожает рейв. Интересно то, что все они были в банданах и рубашках черного, белого и желтого цветов, но цвет банданы и рубашки совпадал только у любителя техно. А у любителя хаус ни рубашка, ни бандана не были белыми. А любитель рейв был в желтой рубашке.

Определите цвет рубашек и бандан каждого из любителей клубной музыки.

Решение

Заметим, что по условию задачи цвет банданы и рубашки совпадал только у любителя техно. А так как у любителя хаус ни рубашка ни бандана не были белыми и любитель рейв был в желтой рубашке, то делаем вывод, что любитель техно может быть в рубашке и бандане только белого цвета.

Получаем граф:

 

 

 

 

Решение сводится к нахождению трех сплошных треугольников с вершинами в разных множествах.

Значит, у любителя хаус желтая бандана и черная рубашка (т.к. цвет совпадал только у любителя техно по усл.), а у любителя рейв черная бандана.

 

Ответ. У любителя техно рубашка и бандана белого цвета;

у любителя хаус черная рубашка и желтая бандана;

у любителя рейв желтая рубашка и черная бандана.

 

 

Задача 1.

Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: "Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский". Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей?

 

Решение.

Запишем условие кратко

Чёрточка сверху означает отрицание.

Имеется три утверждения:

- Вадим изучает китайский;

- Сергей не изучает китайский;

-Михаил не изучает арабский.

Рассмотрим перебор всех случаев.

 

	Вадим К Сергей К Михаил А

1 случай. Верно первое утверждение.

Два других ложны

Получили противоречие

. Двое изучают китайский язык.

 

2 случай. Верно второе утверждение.

Два других ложны

Получили противоречие.

Никто не изучает китайский язык

 

.

3 случай. Верно третье утверждение.

Два других ложны

 

 

Ответ: Сергей изучает китайский язык,

Михаил — японский,

Вадим — арабский.

 

Задача 2.

На концерт пошли три девочки нашего класса Аня, Валя и Люда. Одна из них была в красном платье, другая – в белом, третья – в синем. На вопрос, какое на каждой из девушек было платье, они ответили:

- Аня была в красном.

- Валя – не в красном.

- Люда – не в синем.

В этом ответе из трёх частей одна верна, две неверны.

В каком платье была каждая из девочек?

Решение.

Условие. Запишем условие кратко.

(Чёрточка сверху означает отрицание)

 

 

Рассмотрим перебор всех случаев

Аня К   Валя К   ЛюдаС

1) Если только

первое

высказывание

верно. Получили противоречие.

 

 

2) Если только

второе

высказывание Получили противоречие.

Верно

 

3) Если только Аня К С, Б

третье

высказывание Валя К К

верно

Люда С К, Б

 

Ответ. Валя была в красном платье,

Люда в белом платье,

Аня в синем платье.

 

 

Истинностные задачи

Задача 1.

Василиса Прекрасная

Украли у Ивана Царевича Василису Прекрасную. Поехал он выручать ее. Поймал Змея Горыныча, Бабу Ягу, Кощея Бессмертного и Лешего – Иван Царевич знал, что один из них украл ее.

И спрашивает: «Кто украл Василису?» Змей Горыныч, Баба Яга и Кощей Бессмертный ответили: «Не я», а Леший – «Не знаю».

Потом оказалось, что двое из них сказали правду, а двое – неправду.

Знает ли Леший, кто украл Василису?

Решение

Начнем рассуждать с ответов Змея Горыныча, Бабы Яги, Кощея Бессмертного.

Так как украл Василису Прекрасную кто-то один, то среди ответов Змея Горыныча, Бабы Яги, Кощея Бессмертного может быть лишь один ложный, иначе при двух ложных ответах получается, что украли ее двое.

Тогда вторым ложным ответом будет ответ Лешего, так как всего ложных ответов два.

Поэтому Леший знал, кто украл Василису Прекрасную.

Задача 2.

Незнайка

Незнайка услышал разговор Сиропчика, Пилюлькина, Торопыжки и Знайки.

Известно, что каждый из них либо всегда лжет, либо всегда говорит правду.

1) Сиропчик обвинил Пилюлькина в том, что он – лгун.

2) Знайка сказал Сиропчику: «Сам ты лгун!».

3) Торопыжка заметил: «Оба они лгуны».

4) Знайка спросил у Звезды «А я?».

5) На что Торопыжка ответил «И ты тоже лгун!»

«Кто же из них говорит правду?» - удивился Незнайка.

Помогите ему.

 

 

Решение

Поочередно предположим, что каждый из них говорит правду.

Допустим, что Сиропчик говорит правду.

Тогда, рассмотрев первое высказывание, можно утверждать, что Пилюлькин – лгун,исходя из второго высказывания получаем, что Знайка – лгун.

Третье высказывание приводит нас к противоречию: если Торопыжка говорит правду, то Сиропчик и Пилюлькин лгуны – это противоречит нашему предположению, если Торопыжка лжет, то Сиропчик и Пилюлькин говорят правду – это противоречит первому высказыванию.

Приходим к выводу, что Сиропчик лжет и наше предположение не верно.

Тогда Пилюлькин говорит правду.

Допустим, что Знайка говорит правду.

Тогда, второе высказывание истинно и Сиропчик – лжет.

Мы уже выяснили, что это правда.

Рассмотрев пятое высказывание, приходим к выводу, что Торопыжка лжет.

Таким образом, Знайка и Пилюлькин говорят правду.

Ответ. Знайка и Пилюлькин говорят правду.

 

 

Задачи на переливание

Рассмотрим еще один тип логических задач. Это задачи на переливания, в которых с помощью сосудов известных емкостей требуется отмерить некоторое количество жидкости.

Задача.

Винни-Пух и пчелы

Однажды Винни-Пух захотел полакомиться медом и пошел к пчелам в гости. По дороге нарвал букет цветов, чтобы подарить труженицам пчелкам. Пчелки очень обрадовались, увидев мишку с букетом цветов, и сказали: «У нас есть большая бочка с медом. Мы дадим тебе меда, если ты сможешь с помощью двух сосудов вместимостью 3 л и 5 л налить себе 4 л!» Винни-Пух долго думал, но все-таки смог решить задачку. Как он это сделал?

Решение

Как в результате можно получить 4 л?

Нужно из 5-литрового сосуда отлить 1 л. А как это сделать?

Нужно в 3-литровом сосуде иметь ровно 2 л. Как их получить?

– Из 5-литрового сосуда отлить 3 л. Решение лучше и удобнее оформить в виде таблицы:

 

 

Наполняем из бочки 5-литровый сосуд медом (1 шаг). Из 5-литрового сосуда отливаем 3 л в 3-литровый сосуд (2 шаг). Теперь в 5-литровом сосуде осталось 2 литра меда. Выливаем из 3-литрового сосуда мед назад в бочку (3 шаг). Теперь из 5-литрового сосуда выливаем те 2 литра меда в 3-литровый сосуд (4 шаг). Наполняем из бочки 5-литровый сосуд медом (5 шаг). И из 5-литрового сосуда дополняем медом 3-литровый сосуд. Получаем 4 литра меда в 5-литровом сосуде (6 шаг). Задача решена.

Поиск решения можно было начать с такого действия: к трем литрам добавить 1 литр. Но тогда решение будет

 

 

Задачи на взвешивание

Задачи на взвешивание - достаточно распространённый вид математических задач. В таких задачах от решающего требуется локализовать отличающийся от остальных предмет по весу за ограниченное число взвешиваний. Поиск решения в этом случае осуществляется путем операций сравнения, правда, не только одиночных элементов, но и групп элементов между собой.

 

Задача 1.

Буратино и Кот Базилио

У Буратино есть 27 золотых монет. Но известно, что Кот Базилио заменил одну монету на фальшивую, а она по весу тяжелее настоящих. Как за три взвешивания на чашечных весах без гирь Буратино определить фальшивую монету?

Решение

Разделим монеты на 3 кучки по 9 монет. Положим на чаши весов первую и вторую кучки; по результату этого взвешивания мы точно узнаем, в какой из кучек находится фальшивка (если весы покажут равенство, то она - в третьей кучке). Теперь, аналогично, разделим выбранную кучку на три части по три монеты, положим на весы две из этих частей и определим, в какой из частей находится фальшивая монета. Наконец, остается из трех монет определить более тяжелую: кладем на чаши весов по 1 монете - фальшивкой является более тяжелая; если же на весах равенство, то фальшивой является третья монета из части. Задача решена.

Задача 2.

Золушка

Мачеха послала Золушку на рынок. Дала ей девять монет: из них 8 настоящих, а одна фальшивая – она легче чем настоящая. Как найти ее Золушке за два взвешивания?

Решение

Разделим 9 монет на 3 равных кучки. Положим на чаши весов первую и вторую кучки; по результату этого взвешивания мы точно узнаем, в какой из кучек находится фальшивка (если весы покажут равенство, то она - в третьей кучке). Остается из трех монет определить более легкую: кладем на чаши весов по 1 монете - фальшивкой является более легкая; если же на весах равенство, то фальшивой является третья монета.

 

Задача 3.

Фальшивая монета

Среди 101 одинаковых по виду монет одна фальшивая, отличающаяся по весу. Как с помощью чашечных весов без гирь за два взвешивания определить, легче или тяжелее фальшивая монета? Hаходить фальшивую монету не требуется.

Решение

Взвешиваем 50 и 50 монет: два случая.

1 случай. Равенство. Берем оставшуюся монету и ставим ее в левую кучку вместо одной из имеющихся там:

а) Левая кучка тяжелее => фальшивая монета тяжелее;

б) Левая кучка легче => фальшивая монета легче.

2 случай. Неравенство. Берем более тяжелую кучку и разбиваем ее на две кучки по 25 монет:

а) Вес кучек одинаковый => фальшивая монета легче;

б) Вес кучек неодинаковый => фальшивая монета тяжелее.

 

Задача 4.

Фальшивая монета 2

Имеется 8 монет. Одна из них фальшивая и легче настоящей монеты. Определите за 3 взвешивания какая из монет фальшивая.

Решение

Делим монеты на две равные кучки – по 4 монеты в каждой. Взвешиваем. Ту кучку, которая легче, опять делим на две одинаковых кучки – теперь по две монеты в каждой. Взвешиваем. Определяем, какая из них легче. Кладем на чаши весов по 1 монете из этой кучки. Фальшивая та, которая легче. Задача решена.

 

Задача 5.

 

Фальшивая монета 3

Имеется 10 монет. Одна из них фальшивая и легче настоящей монеты. Как, с помощью чашечных весов без гирь, определить какая из монет фальшивая?

Решение

Разделим 10 монет на 2 равных кучки – по 5 монет. Положим на чаши весов. Определим, в какой из этих кучек находится фальшивая монета. Теперь эту кучку делим на 3 кучки – в двух из них по две монеты, в третьей одна монета. Взвешиваем кучки, в которых по две монеты. Если весы покажут равенство, то фальшивка в третьей кучке. Если покажут неравенство, то фальшивая монета в кучке, которая легче. Теперь кладем на чаши весов по 1 монете из этой кучки – фальшивкой является более легкая. Задача решена.

 

 

Задача 6.

 

Лиса Алиса и Кот Базилио

Лиса Алиса и Кот Базилио – фальшивомонетчики. Базилио делает монеты тяжелее настоящих, а Алиса – легче. У Буратино есть 15 одинаковых по внешнему виду монет, но какая-то одна – фальшивая. Как двумя взвешиваниями на чашечных весах без гирь Буратино может определить, кто сделал фальшивую монету – Кот Базилио или Лиса Алиса?

Решение

Буратино может разделить свои монеты на три кучки по 7, 4, 4, или по 5, 5, 5, или по 3, 6, 6, или по 1, 7, 7 монет. При первом взвешивании он положит на весы две кучки монет одинаковой величины. Если при этом весы оказались в равновесии, значит, все монеты на весах настоящие, а бракованная монета в оставшейся кучке. Тогда при втором взвешивании на одну чашку весов Буратино положит кучку с бракованной монетой, а на вторую – столько настоящих монет, сколько всего монет он положил на первую чашку, и тогда он сразу определит, легче фальшивая монета, чем настоящие, или тяжелее. Если же при первом взвешивании весы оказались не в равновесии, значит, все монеты в оставшейся кучке настоящие. Тогда Буратино уберет с весов легкую кучку, а монеты из тяжелой кучки разделит на две равные части и положит на весы (если в кучке было 5 или 7 монет, предварительно добавит к ним одну настоящую монету). Если при втором взвешивании весы оказались в равновесии,значит, фальшивая монета легче настоящих, а если нет, то тяжелее. Задача решена.

 

Задача 7.

 

Буратино

Буратино имеет четыре одинаковых по виду монеты, одна из которых не золотая, а фальшивая и легче других. Как Буратино определить фальшивую монету? Какое минимальное число взвешиваний ему потребуется?

Решение

Разделим монеты на 2 равных кучки – по 2 монеты. Положим на чаши весов. В более легкой кучке находится фальшивая монета. Теперь кладем на чаши весов по 1 монете из этой кучки – фальшивкой является более легкая. Буратино потребуется два взвешивания. Задача решена.

 

ЗАДАЧИ РАЗНЫЕ

 

Задача 2.

В одном доме живут три товарища - школьники Боря, Вася и Дима.

Один из них играет в футбольной команде, другой пишет стихи, а третий лучше своих друзей играет в шахматы.

Известно, что: 1) Васин друг с огорчением сказал: «Вчера я не сумел реализовать пенальти»;

2) товарищ поэта сказал: «Дима! Написал бы ты стих и для нашей футбольной команды».

Назовите имена футболиста, поэта и шахматиста.

3. В стакане находятся бактерии. Через секунду каждая из бактерий делится пополам, затем каждая из получившихся бактерий через секунду делится пополам и так далее. Через минуту стакан полон. Через какое время стакан был заполнен наполовину?

 

4. Из книги выпал кусок, первая страница которого имеет номер 23, а номер последней записывается теми же цифрами в каком-то другом порядке. Сколько страниц в выпавшем куске?

5. В мешке 24 кг гвоздей. Как, имея только весы без гирь, отмерить 9 кг гвоздей?

6. Петя говорит: позавчера мне еще было 10 лет, а в следующем году мне исполнится 13. Может ли такое быть?

7. Учитель рисует на листке бумаги несколько кружков и спрашивает одного ученика:

«Сколько здесь кружков?». «Семь»– отвечает ученик. «Правильно. Так сколько здесь

кружков?» – опять спрашивает учитель другого ученика. «Пять» – отвечает тот.

«Правильно» – снова говорит учитель. Так сколько же кружков он нарисовал на листке?

8. Гном разложил свои сокровища в 3 сундука разного цвета, стоящих у стены: в один – драгоценные камни, в другой – золотые монеты, в третий – магические книги. Он помнит, что красный сундук находится правее, чем камни, и что книги – правее красного сундука. В каком сундуке лежат книги, если зеленый сундук стоит левее синего?

9. Коля считает, что если сумма первых трех цифр номера автобусного билета равна сумме последних трех цифр, то билет – счастливый. Билет с номером 198675 – счастливый. Какие два ближайших к нему билета тоже счастливые?

10. Какой цифрой оканчивается выражение 4891 x 4892 x 4893 x 4894 x 4895?

11. Какими двумя цифрами оканчивается выражение 79 x 25 x 83 x 16 – 43288?

12. В классе все дети изучают английский и французский языки. Из них 17 человек изучают английский, 15 человек – французский, а 8 человек изучают оба языка одновременно. Сколько учеников в классе?

13. Магазин получил со склада 1000 линеек. Одни из них имеют длину 20 см, а другие 30 см. Общая длина линеек 220 м. Сколько 20-сантиметровых линеек получил магазин?

14. Если считать этаж, на котором живет Катя, сверху, то получится вшестеро больше, чем если считать снизу. На каком этаже живет Катя, если в ее доме больше 10 и меньше 20 этажей?

15. Сложи из шести спичек четыре треугольника.

16. Электрические настенные часы со стрелками отстают каждые сутки на 6 минут. Хозяин поставил их на верное время, а сам уехал в командировку. Когда он вернулся, часы опять показывали верное время. Сколько суток он отсутствовал?

 

17. Две ученицы, Люда и Валя, победили в математической олимпиаде. Нужно было выяснить, кому из них дать первую премию, а кому вторую. Судья соревнования показал им три заколки: одну красную и две синие, попросил их зажмуриться и приколол к их прическам по красной заколке, а синюю спрятал. После этого он сказал, что они могут открыть глаза. "Кто догадается, – сказал судья, – какого цвета на ней заколка, та получит первую премию." Девочки смотрели друг на друга. Каждая видела на другой красную заколку, но не знала, какая заколка на ней. Наконец, Люда сказала: "На мне красная заколка" – и получила первую премию. Как она могла додуматься до верного ответа?

18. Среди 12 щенков 8 ушастых и 9 кусачих, и других нет. Сколько среди этих щенков ушастых и кусачих одновременно?

19. Гавиал, кашалот и пеликан съели 31 рыбу. Кашалот съел рыб во столько раз больше, чем пеликан, во сколько пеликан съел больше гавиала. Сколько рыб съел каждый из них?

20. Муравей сидит на передней грани куба в точак А и желает попасть на верхнюю грань в точку В. Как узнать, по какому кратчайшему пути должен он ползти?

21. Брошены два игральных кубика. Какая сумма очков на их верхних гранях наиболее вероятна?

22. Андрей, Борис, Вадим и Геннадий заняли первые четыре места в соревновании по перетягиванию каната. На вопрос корреспондента, какое место занял каждый из них, было получено три ответа:

1) Андрей – первое, Борис – второе,
2) Андрей – второе, Геннадий – третье,
3) Вадим – второе, Геннадий – четвертое.

В каждом из этих ответов одна часть правдива, а вторая ложна. Кто занял какое место?

23. 4 человека стоят у лифта 5-этажного дома. Все они живут на разных этажах, от второго до пятого. Лифтер хочет доехать до одного какого-нибудь этажа, а там пусть идут пешком. Спуститься на один этаж – неудовольствие, подняться на один этаж – двойное неудовольствие. На каком этаже надо остановить лифт, чтобы сумма неудовольствий была наименьшей?

24. Этими кубиками написано число 7. Какие числа надо написать на гранях двух кубиков, чтобы получился календарь, то есть чтобы можно было писать кубиками все числа от 01 до 31?

 

25. Я вошел в комнату, чтобы взять из шкафа свои ботинки и носки. В комнате спала сестра, и было совсем темно, Я знал, в каком месте шкафа находятся мои три пары ботинок — все разных фасонов, и 12 пар носков — черных и коричневых. Мне не хотелось зажигать свет, чтобы не разбудить сестру. Как ботинки, так и носки я обнаружил на своих местах, но, в беспорядке— просто груду из 6 ботинок и кучу из 24 носков Сколько ботинок и сколько носков (самое меньшее) мне надо вынести из темной комнаты в светлую, чтобы обеспечить себя парой ботинок одного фасона и парой носков одного цвета?

26. В соревновании по бегу уча­ствовали три бегуна: Авдеев. Васильев и Семенов. Перед за­бегом один зритель сказал, что первым придет Авдеев, вто­рой — что Семенов не будет по­следним, а третий — что Васи­льев не придет первым. После забега оказалось, что один зри­тель угадал, а два других ошиблись. Как закончились со­ревнования?

27. Во время перемены в классе оставались 4 шестиклассника: Андрей, Виктор,

Денис и Марат. Кто-то из них разбил стекло. Учитель, опросив ребят, установил, что только один из них сказал правду.

Андрей: «Стекло разбил

Виктор». Виктор: «Виноват Марат». Денис: «Стекло разбил не я».

Марат: «Виктор лжёт».

Как вы думаете, кто разбил стекло?

28. Учитель математики, проверив олимпиадные работы учеников, сказал, что первые три места заняли Сергей, Василий и Алексей, причём Сергей занял не первое место, Василий - не второе, а Алексей - второе место. Определите, кто какое место занял на олимпиаде, если оказалось, что учитель в двух высказываниях ошибся.

29. Встретились три бывших одноклассника — Влад, Тимур и Юра.

Известно что:

1) один из них стал врачом, другой физиком, а третий юристом;

2) один полюбил туризм, другой бег, страсть третьего — регби

3) Юра сказал, что на туризм ему не хватает времени, хотя его сестра —

единственный врач в семье, заядлый турист

4) врач сказал, что он разделяет увлечение коллеги

5) у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен. Определите, кто чем любит заниматься в свободное время и у кого какая профессия.

30. Трое сестёр: Дина, Анна и Лида занимаются разными видами искусств - пением, балетом и кино. Все они живут в разных городах: в Петербурге, Риме и Киеве. Известно что:

1) Дина живёт не в Петербурге, а Лида не в Риме;

2) та которая живёт в Петербурге не снимается в кино;

3) та которая живёт в Риме, певица;

4) Лида равнодушна к балету.

Где живёт Анна, и какова её профессия?

31. Кто из трёх мальчиков А,Б и В играет в шахматы, если известно:

1) из А и Б один играет, один - не играет;

2) если играет А, то играет и Б;

3) А и В оба играют или оба не играют.

32. В коробке 30 конфет: шоколадных и карамелей. Известно, что среди любых 12-ти конфет имеется хотя бы одна карамель, а среди любых 20-ти конфет имеется хотя бы одна шоколадная.

Сколько в коробке шоколадных конфет и сколько карамелей?

33. Для поездки с учениками за город школа заказала несколько одинаковых автобусов, 115 человек поехали на озеро, 138 - в лес, Все места в автобусах были заняты, и всем хватило места, Сколько было заказано автобусов и сколько мест в каждом автобусе?

34. В одном доме живут три товарища - школьники Боря, Вася и Дима. Один из них играет в футбольной команде, другой пишет стихи, а третий лучше своих друзей играет в шахматы. Известно, что:

1) Васин друг с огорчением сказал: «Вчера я не сумел реализовать пенальти»;

2) товарищ поэта сказал: «Дима! Написал бы ты стих и для нашей футбольной команды». Назовите имена футболиста, поэта и шахматиста.

35. Сколько горшочков мёда у Вини-Пуха, если:

1) увеличив их количество на 25 штук, получим горшочков больше 51, но меньше 62;

2) уменьшив первоначальное количество горшочков на 18 штук, получим больше, чем 16, но меньше, чем 26;

3) увеличив первоначальное количество горшочков в 5 раз, получим горшочков больше, чем 175, но меньше, чем 205?

36. Помогите Буратино разложить 9 монет, достоинством 1 золотой, 2 золотых, 3 золотых,..., 9 золотых в 3 кошелька так, чтобы в первом было 2 монеты, во втором - 3 монеты, в третьем - 4 монеты, а сумма в кошельках была одинаковой.

37. Прикрыв рукой половину циферблата наручных часов, Коля заметил, что сумма закрытых цифр, равна сумме оставшихся открытыми. Какую половину циферблата прикрыл Коля?

38. На столе 3 совершенно одинаковых ящичка. В одном из них лежат 2 черных шарика, в другом — черный и белый, в третьем — 2 белых. На ящичках есть надписи: «2 черных», «2 белых», «Черный и белый», однако известно, что ни одна из этих надписей не соответствует действительности. Сможете ли вы определить, где какие шарики лежат, вынув всего один шарик из какой-нибудь коробки?

 

39. Пятачок, покупая воздушные шарики, раскладывал их в 6 карманов своей одежды так, что в каждом кармане лежит не менее одного, но не более шести шариков, при этом в каждом кармане разное количество шариков. В какую сумму обошлась Пяточку покупка, если каждый шарик стоит 1 грн.?

40. Коля и Вася живут в одном доме, на каждой лестничной клетке которого 4 квартиры, Коля живет на пятом этаже, в квартире 83, а Вася на 3-ем этаже в квартире 169, Сколько этажей в доме?

41. В конкурсе должно было принять участие некоторое количество учеников. Известно, что: 1) если бы их пришло на 37 человек больше, то количество участников было бы больше 70, но меньше 92; 2) если бы их пришло на 28 человек меньше, то количество участников было бы больше, чем 11, но меньше, чем 15.

Сколько школьников должно было участвовать в конкурсе, если от каждой параллели (5-11 кл.) планировалось участие равного количества учеников?

42. Чебурашка поселился в высотном здании. На каком этаже находится его квартира, если: 1) поднявшись со