Постановка транспортной задачи (ТЗ)
Пусть, X= ( x ij) – m* n матрица, где xij – объем перевозок от i-го поставщика к j-му потребителю. Тогда общие затраты на перевозку груза определяются функцией :
m n
z(X)= å å cijxij.
i=1 j=1
Математически постановка транспортной задачи определяется следующей задачей линейного программирования :
m n
z(X) = å å cij xij min, при условиях
i=1 j=1
m
å xij= bj, j=1,…., n,
i=1
n
å xij = ai, i= 1,….., m,
J= 1
xij ≥ 0
Первая часть нетривиальных ограничений означает, что все потребности удовлетворены, вторая часть, что весь груз вывезен от поставщиков.
Открытая и закрытая модели.
Транспортная задача называется задачей с правильным балансом, а ее модель закрытой, если: m n
å ai = å bj,
i =1 j =1
т, е суммарные запасы поставщиков равны суммарным запросам потребителей.
Если: m n
å ai ≠ å bj
i=1 j=1
то такая задача называется задачей с неправильным балансом, а её модель – открытой.
3. Методы построения опорного плана – метод минимального тарифа.
Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую и в клетку, которая ей соответствует, помещают меньшее из чисел ai и bj Затем из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.
Метод Фогеля.
Метод Фогеля состоит в вычислении для каждой строки транспортной таблицы разницы между двумя наименьшими тарифами. Аналогичное действие выполняют для каждого столбца этой таблицы. Наибольшая разница между двумя минимальными тарифами соответствует наиболее предпочтительной строке или столбцу (если есть несколько строк или столбцов с одинаковой разницей, то выбор между ними произволен). В пределах этой строки или столбца отыскивают ячейку с минимальным тарифом, куда пишут отгрузку. Строки поставщиков или столбцы потребителей, которые полностью исчерпали свои возможности по отгрузке или потребности которых в товаре были удовлетворены, вычеркиваются из таблицы, и вычисление повторяются до полного удовлетворения спроса и исчерпания отгрузок без учета вычеркнутых ячеек. Методом Фогеля обычно получается план, близкий к оптимальному, или сам оптимальный план.
Занятые и свободные клетки.
Клетки таблицы транспортной задачи, в которых находится отличные от нуля или базисные нулевые перевозки, называются занятыми, остальные – незанятыми или свободными. Клетки таблицы нумеруются так, что клетка, содержащая перевозку , т.е. стоящая в i-й строке и j-м столбце, имеет номер (i,j). Каждой клетке с номером (i,j) соответствует переменная, которой соответствует вектор-условие.
6. Вырожденные и невырожденные планы.
В общем случае опорный план транспортной задачи состоит из m+ n−1 занятой клетки (по числу базисных переменных). Такой план называется невырожденным. Нередко при решении транспортной задачи возникает вырожденный план с меньшим числом занятых клеток (когда какие-то из базисных переменных равны 0).
Постановка задачи многокритериальной оптимизации.
Задача вида
fi (x) -> max (min)
x ÎD
где, I>1, DÎR n – допустимое множество, а f i(x) – гладкие функции на D, называется задачей многокритериальной оптимизации.
Доминирование и оптимальность по Парето. Эффективные решения и Парето –оптимальная (Парето –эффективная ) граница.
Пусть X и Y – два допустимых решения. Говорят, что Х доминирует Y, если для всех I= 1,2,….n выполнятся неравенство fi (X) ≥ fi (Y) и найдется такое k, что fk(X)>fk(Y).
Решение Z называется недоминируемым (эффективным), если нет решения Х, которое бы доминировало Z.
Множество эффективных (недоминируемых) решений называется множеством Парето. Геометрическое изображение множества Парето называется Парето-эффективной границей (Парето-оптимальной границей)
Доминируемые стратегии.
Если в платежной матрице Р все элементы i –й строки не меньше соответствующих элементов k-й строки, а aij ≥akj, j=1,n, а по крайней мере один строго больше, то
i-я строка называется доминирующей, а k-я строка доминируемой.
22. Решение игр в смешанных стратегиях.
Если a<b, то применение чистых стратегий не дает оптимального решения игры. Его можно получить случайным образом чередуя чистые стратегии, т.е в смешанных стратегиях.
ОПРЕДЕЛЕНИЕ: Смешанной стратегией SА игрока А называется применение
m
чистых стратегий А1,А2,….., Аm с вероятностями p1,p2,…..,pm, åpi = 1.
i=1
SА = А1 А2 … Аm
P1 P2 … Pm
Аналогично для игрока В:
B1 B2 … Bn n
SB = q1 q2 … qn , å qj=1
j=1
ТЕОРЕМА НЕЙМАНА: Каждая конечная игра имеет, по крайней мере, одно оптимальное решение, возможно, среди смешанных стратегий.
23. Графическое решение игр вида 2 * n и m * 2.
У таких игр всегда имеется решение, содержащее не более двух активных стратегий для каждого из игроков. Если найти эти активные стратегии, то игра 2 х n или m х 2 сводится к игре 2 х 2.
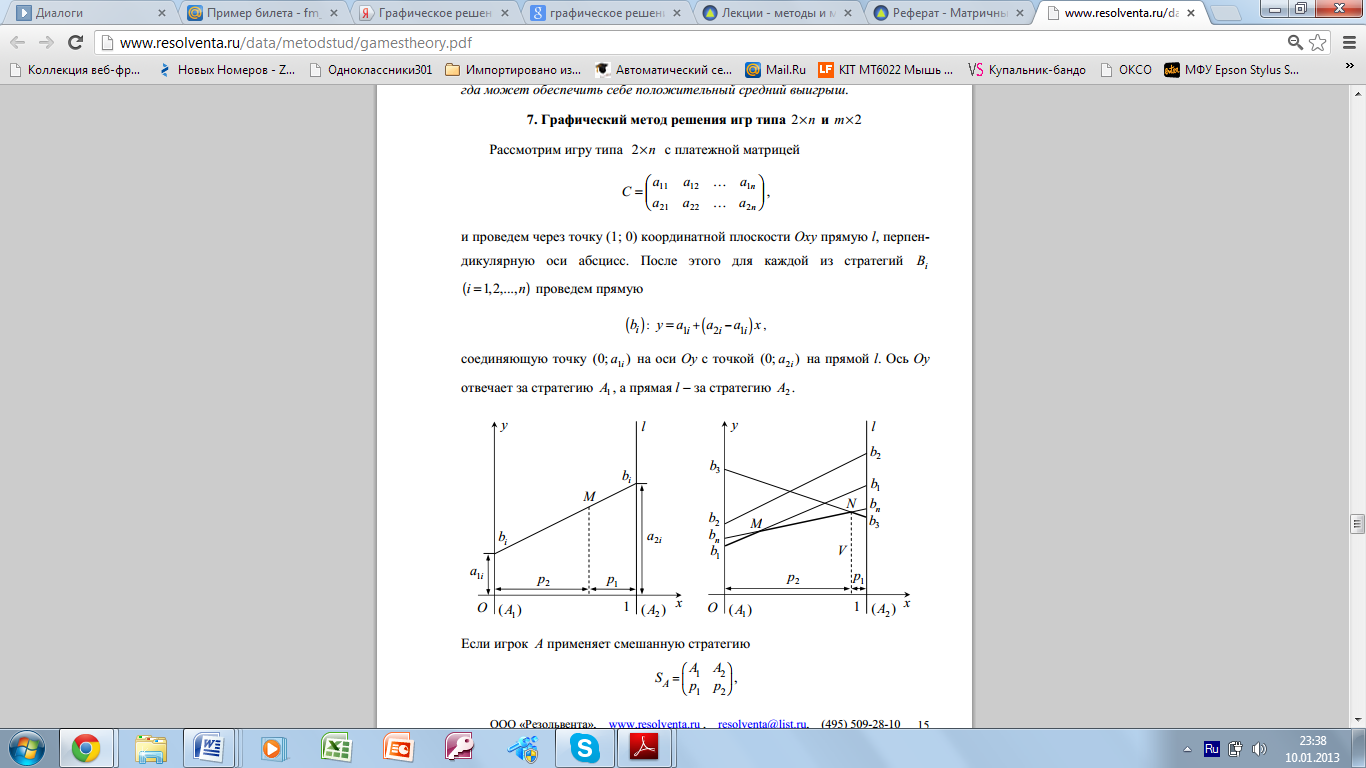
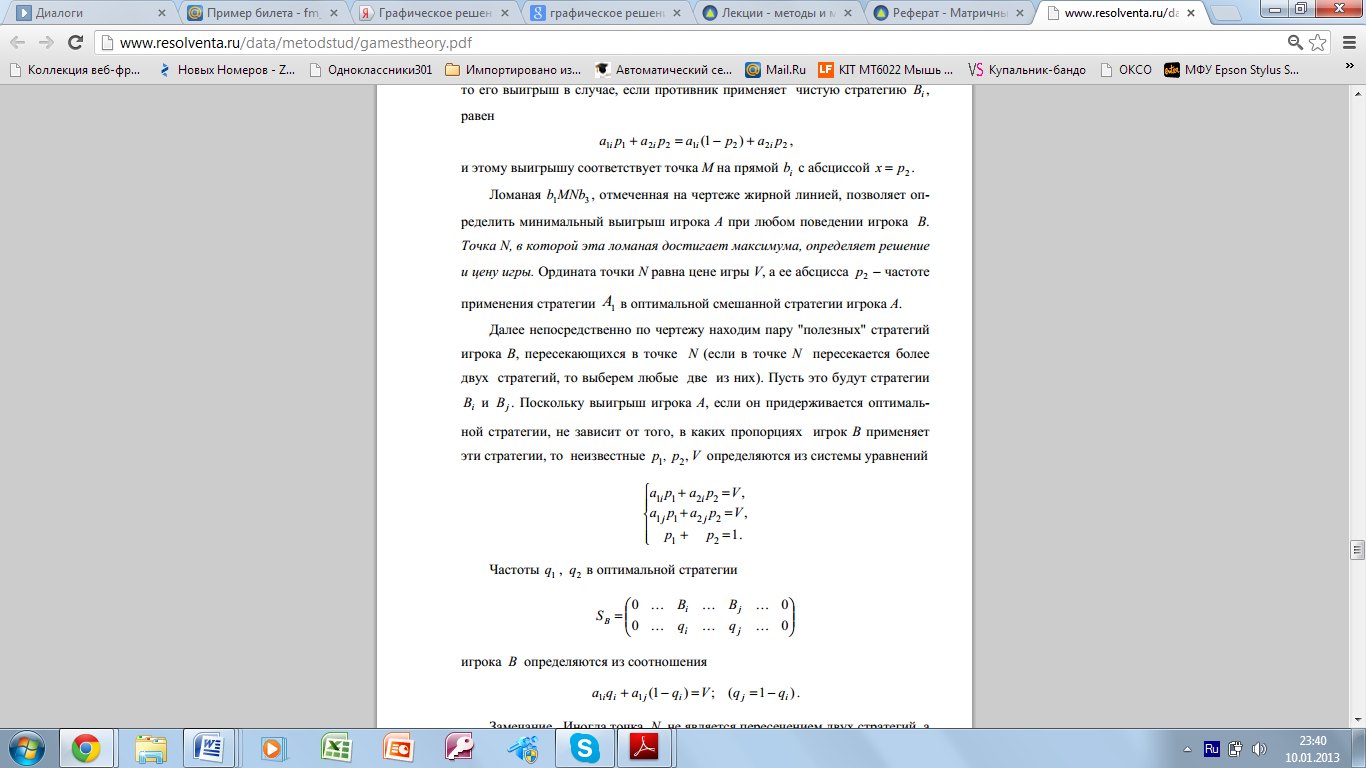 Для игры m*2 решение находится совершенно аналогично. Действительно, поскольку выигрыш игрока А одновременно является проигрышем игрока В, то для решения задачи нужно построить ломаную, соответствующую верхней границе выигрыша игрока А, а затем найти на ней точку с минимальной ординатой.
Для игры m*2 решение находится совершенно аналогично. Действительно, поскольку выигрыш игрока А одновременно является проигрышем игрока В, то для решения задачи нужно построить ломаную, соответствующую верхней границе выигрыша игрока А, а затем найти на ней точку с минимальной ординатой.
24. Метод динамического программирования. Принцип оптимальности и уравнение Беллмана.
Метод динамического программирования состоит в том что оптимальное управление строится постепенно. На каждом шаге оптимизируется управление только этого шага. Вместе с тем на каждом шаге управление выбирается с учётом последствий, так как управление, оптимизирующее целевую функцию только для данного шага, может привести к неоптимальному эффекту всего процесса. Управление на каждом шаге должно быть оптимальным с точки зрения процесса в целом. Это основное правило динамического программирования, сформулированное Беллманом, называется принципом оптимальности.
Так, если система в начале k - шага находится в состоянии 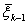 и мы выбираем произвольное управление
и мы выбираем произвольное управление 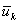 , то она придет в новое состояние в
, то она придет в новое состояние в 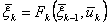 , и последующие управления
, и последующие управления 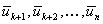 должны выбираться оптимальными относительно состояния
должны выбираться оптимальными относительно состояния 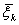 . Последнее, означает, что этих управлениях максимизируется величина
. Последнее, означает, что этих управлениях максимизируется величина 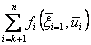 , то есть показатель эффективности на последующих до конца процесса шагах
, то есть показатель эффективности на последующих до конца процесса шагах 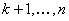 . Обозначим через
. Обозначим через 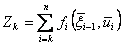 .
.
Выбрав оптимальное управление 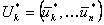 на оставшихся
на оставшихся 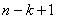 шагах, получим величину
шагах, получим величину 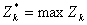 , которая зависит только от
, которая зависит только от 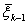 , то есть
, то есть 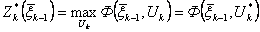 .
.
Назовем величину 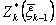 условным максимумом. Если мы теперь выберем на k-м шаге некоторое произвольное управление
условным максимумом. Если мы теперь выберем на k-м шаге некоторое произвольное управление 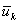 , то система придет в состояние
, то система придет в состояние 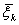 . Согласно принципу оптимальности, необходимо выбирать управление
. Согласно принципу оптимальности, необходимо выбирать управление 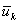 так, чтобы оно в совокупности с оптимальным управлением на последующих шагах (начиная с (k +1)-го) приводило бы к общему показателю эффективности на
так, чтобы оно в совокупности с оптимальным управлением на последующих шагах (начиная с (k +1)-го) приводило бы к общему показателю эффективности на 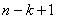 шагах, начиная с k-uго и до конца. Это положение в аналитической форме можно записать в виде следующего соотношения:
шагах, начиная с k-uго и до конца. Это положение в аналитической форме можно записать в виде следующего соотношения:
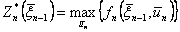 ,
,
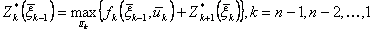 , (1)
, (1)
получившего название основного функционального уравнения динамического программирования, илиосновного рекуррентного уравнения Беллмана.
Из уравнения (1) может быть получена функция 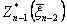 , если известно функция
, если известно функция 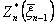 . Аналогично можно получить
. Аналогично можно получить 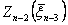 , если известно
, если известно 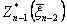 и т. д., пока не будет определена величина
и т. д., пока не будет определена величина 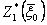 , представляющая по определению максимальное значение показателя эффективности процесса в целом:
, представляющая по определению максимальное значение показателя эффективности процесса в целом:
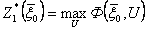 .
.
Решая уравнение (1) для определения условного максимума показателя эффективности за 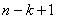 шагов, начиная с k-го, мы определяем соответствующее оптимальное управление
шагов, начиная с k-го, мы определяем соответствующее оптимальное управление 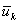 , при котором этот максимум достигается. Это управление также зависит от
, при котором этот максимум достигается. Это управление также зависит от 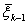 ; будем обозначать его через
; будем обозначать его через 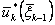 и называть условным оптимальным управлением на k-м шаге. Основное значение уравнения (1), в котором реализована идея динамического программирования, заключается в том, что решение исходной задачи определения максимума функции
и называть условным оптимальным управлением на k-м шаге. Основное значение уравнения (1), в котором реализована идея динамического программирования, заключается в том, что решение исходной задачи определения максимума функции 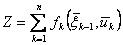 n переменных
n переменных 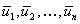 сводится к решению последовательности nзадач, задаваемых соотношениями (1), каждое из которых является задачей максимизации функции одной переменной
сводится к решению последовательности nзадач, задаваемых соотношениями (1), каждое из которых является задачей максимизации функции одной переменной 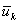 .
.
В результате последовательного решения п частных задач на условный максимум определяют две последовательности функций: 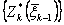 - условные максимумы и соответствующие им
- условные максимумы и соответствующие им 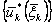 - условные оптимальные управления. Указанные последовательности функций в дискретных задачах получают в табличной форме, а в непрерывных моделях - аналитически. После выполнения первого этапа (условнойоптимизациии) приступают ко второму этапу - безусловной оптимизации.
- условные оптимальные управления. Указанные последовательности функций в дискретных задачах получают в табличной форме, а в непрерывных моделях - аналитически. После выполнения первого этапа (условнойоптимизациии) приступают ко второму этапу - безусловной оптимизации.
Если начальное состояние 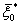 задано
задано 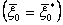 , то непосредственно
, то непосредственно
определяют максимум целевой функции
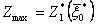 ,
,
а затем - искомое безусловное оптимальное управление по цепочке
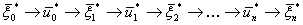 . (2)
. (2)
Если задано множество 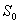 начальных состояний
начальных состояний 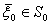 , то дополнительно решают еще одну задачу на максимум
, то дополнительно решают еще одну задачу на максимум
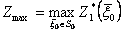 ,
,
откуда находят 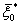 , а затем по цепочке (2) - безусловное оптимальное управление.
, а затем по цепочке (2) - безусловное оптимальное управление.
В рассмотренных рекуррентных соотношениях предписывают начинать вычисления с последнего этапа и затем передвигаться назад до этапа 1. Такой метод вычислений известен как алгоритм обратной прогонки. Если расчеты осуществляются в естественном порядке следования этапов, то такой метод вычислений известен как алгоритм прямой прогонки.
Приведем рекуррентные соотношения для этого случая. Уравнения состояний для прямого хода удобно записывать в виде
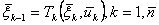 .
.
Введем в рассмотрение условные максимумы показателя эффективности за k шагов, от 1-го до k -говключительно, - величину 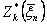 . Повторив приведенные рассуждения, придем к следующей системе уравнений Беллмана:
. Повторив приведенные рассуждения, придем к следующей системе уравнений Беллмана:
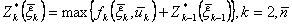 ;
;
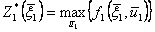 .
.
В результате решения этих уравнений получим последовательности
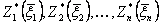 ;
; 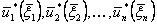 .
.
Далее определим безусловное оптимальное управление по цепочке
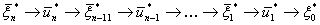 .
.
Постановка транспортной задачи (ТЗ)
Пусть, X= ( x ij) – m* n матрица, где xij – объем перевозок от i-го поставщика к j-му потребителю. Тогда общие затраты на перевозку груза определяются функцией :
m n
z(X)= å å cijxij.
i=1 j=1
Математически постановка транспортной задачи определяется следующей задачей линейного программирования :
m n
z(X) = å å cij xij min, при условиях
i=1 j=1
m
å xij= bj, j=1,…., n,
i=1
n
å xij = ai, i= 1,….., m,
J= 1
xij ≥ 0
Первая часть нетривиальных ограничений означает, что все потребности удовлетворены, вторая часть, что весь груз вывезен от поставщиков.
Открытая и закрытая модели.
Транспортная задача называется задачей с правильным балансом, а ее модель закрытой, если: m n
å ai = å bj,
i =1 j =1
т, е суммарные запасы поставщиков равны суммарным запросам потребителей.
Если: m n
å ai ≠ å bj
i=1 j=1
то такая задача называется задачей с неправильным балансом, а её модель – открытой.
3. Методы построения опорного плана – метод минимального тарифа.
Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую и в клетку, которая ей соответствует, помещают меньшее из чисел ai и bj Затем из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.
Метод Фогеля.
Метод Фогеля состоит в вычислении для каждой строки транспортной таблицы разницы между двумя наименьшими тарифами. Аналогичное действие выполняют для каждого столбца этой таблицы. Наибольшая разница между двумя минимальными тарифами соответствует наиболее предпочтительной строке или столбцу (если есть несколько строк или столбцов с одинаковой разницей, то выбор между ними произволен). В пределах этой строки или столбца отыскивают ячейку с минимальным тарифом, куда пишут отгрузку. Строки поставщиков или столбцы потребителей, которые полностью исчерпали свои возможности по отгрузке или потребности которых в товаре были удовлетворены, вычеркиваются из таблицы, и вычисление повторяются до полного удовлетворения спроса и исчерпания отгрузок без учета вычеркнутых ячеек. Методом Фогеля обычно получается план, близкий к оптимальному, или сам оптимальный план.
Занятые и свободные клетки.
Клетки таблицы транспортной задачи, в которых находится отличные от нуля или базисные нулевые перевозки, называются занятыми, остальные – незанятыми или свободными. Клетки таблицы нумеруются так, что клетка, содержащая перевозку , т.е. стоящая в i-й строке и j-м столбце, имеет номер (i,j). Каждой клетке с номером (i,j) соответствует переменная, которой соответствует вектор-условие.
6. Вырожденные и невырожденные планы.
В общем случае опорный план транспортной задачи состоит из m+ n−1 занятой клетки (по числу базисных переменных). Такой план называется невырожденным. Нередко при решении транспортной задачи возникает вырожденный план с меньшим числом занятых клеток (когда какие-то из базисных переменных равны 0).




 Для игры m*2 решение находится совершенно аналогично. Действительно, поскольку выигрыш игрока А одновременно является проигрышем игрока В, то для решения задачи нужно построить ломаную, соответствующую верхней границе выигрыша игрока А, а затем найти на ней точку с минимальной ординатой.
Для игры m*2 решение находится совершенно аналогично. Действительно, поскольку выигрыш игрока А одновременно является проигрышем игрока В, то для решения задачи нужно построить ломаную, соответствующую верхней границе выигрыша игрока А, а затем найти на ней точку с минимальной ординатой.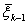 и мы выбираем произвольное управление
и мы выбираем произвольное управление 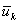 , то она придет в новое состояние в
, то она придет в новое состояние в 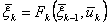 , и последующие управления
, и последующие управления 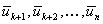 должны выбираться оптимальными относительно состояния
должны выбираться оптимальными относительно состояния 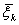 . Последнее, означает, что этих управлениях максимизируется величина
. Последнее, означает, что этих управлениях максимизируется величина 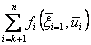 , то есть показатель эффективности на последующих до конца процесса шагах
, то есть показатель эффективности на последующих до конца процесса шагах 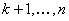 . Обозначим через
. Обозначим через 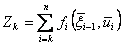 .
.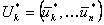 на оставшихся
на оставшихся 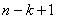 шагах, получим величину
шагах, получим величину 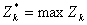 , которая зависит только от
, которая зависит только от 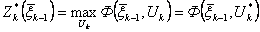 .
.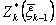 условным максимумом. Если мы теперь выберем на k-м шаге некоторое произвольное управление
условным максимумом. Если мы теперь выберем на k-м шаге некоторое произвольное управление 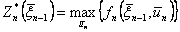 ,
,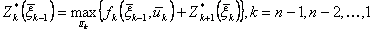 , (1)
, (1)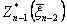 , если известно функция
, если известно функция 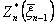 . Аналогично можно получить
. Аналогично можно получить 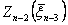 , если известно
, если известно 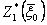 , представляющая по определению максимальное значение показателя эффективности процесса в целом:
, представляющая по определению максимальное значение показателя эффективности процесса в целом: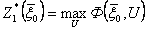 .
.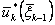 и называть условным оптимальным управлением на k-м шаге. Основное значение уравнения (1), в котором реализована идея динамического программирования, заключается в том, что решение исходной задачи определения максимума функции
и называть условным оптимальным управлением на k-м шаге. Основное значение уравнения (1), в котором реализована идея динамического программирования, заключается в том, что решение исходной задачи определения максимума функции 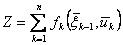 n переменных
n переменных 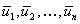 сводится к решению последовательности nзадач, задаваемых соотношениями (1), каждое из которых является задачей максимизации функции одной переменной
сводится к решению последовательности nзадач, задаваемых соотношениями (1), каждое из которых является задачей максимизации функции одной переменной 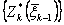 - условные максимумы и соответствующие им
- условные максимумы и соответствующие им 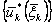 - условные оптимальные управления. Указанные последовательности функций в дискретных задачах получают в табличной форме, а в непрерывных моделях - аналитически. После выполнения первого этапа (условнойоптимизациии) приступают ко второму этапу - безусловной оптимизации.
- условные оптимальные управления. Указанные последовательности функций в дискретных задачах получают в табличной форме, а в непрерывных моделях - аналитически. После выполнения первого этапа (условнойоптимизациии) приступают ко второму этапу - безусловной оптимизации.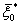 задано
задано 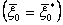 , то непосредственно
, то непосредственно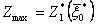 ,
,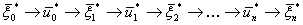 . (2)
. (2)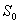 начальных состояний
начальных состояний 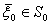 , то дополнительно решают еще одну задачу на максимум
, то дополнительно решают еще одну задачу на максимум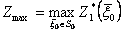 ,
,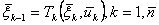 .
.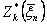 . Повторив приведенные рассуждения, придем к следующей системе уравнений Беллмана:
. Повторив приведенные рассуждения, придем к следующей системе уравнений Беллмана: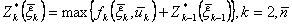 ;
;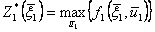 .
.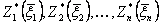 ;
; 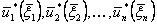 .
.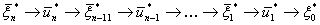 .
.


