U – универсальная машина Тьюринга
Требуется построить м.т. U реализующую описанный алгоритм воспроизведения вычисляющую функцию от двух переменных сист команд 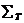
 где α – исходное слово не ленте если м.т. останавливается при исход данных U
где α – исходное слово не ленте если м.т. останавливается при исход данных U
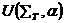 не останавливается если м.т. при исход данных не останавливается.
не останавливается если м.т. при исход данных не останавливается.
Всякая машина обладающими этими свойствами назыв универ м.т.
Существование у.м.т. означает что систему команд 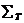 можно понимать двояко: конкретного устройства, либо как программу у.м.т.
можно понимать двояко: конкретного устройства, либо как программу у.м.т.
Интуитивное определение алгоритма.
Алгоритмом назыв совокупность правил обладающих свойствами: массовости (инвариантность относительно входной информации), детерминированности однозначность применения правил на каждом шаге:
Элементарности(отсутствие необходимости уточнения правил) Результативности(получение после конечного числа шагов информвци являющейся результатом)
Тезис Тьюринга
Для любого алгоритма понимаемо в интуитивном смысле можно построить м.т. функционирование которой эквивалентно этому алгоритму.
2 –я формулировка.
Всякий алгоритм может быть реализован м.т.
Подтверждением м.т.: математическая практика, описанная в алгоритме, в любой другой агоритмичесской модели может быть сведено к описанию работы м.т.
Проблема остановки
В числе требований к алгоритмам имеется требование результативности Алгоритм AL и данные α
Приведет ли к результату работа алгоритма AL по данным α
Иначе можно ли построить м.т. Т0 такую что для любой м.т. и любоых исходных данных α  (истина) если м.т. от α останавливается и
(истина) если м.т. от α останавливается и  (ложь) если Т(α) не останавливает эта проблема остановки.
(ложь) если Т(α) не останавливает эта проблема остановки.
Т/ Не сущ м.т. Т0 раскрывающей проблему остановки для произвольной м.т. Т
Рекурсивные Функции
Уточнение понятия алгоритма «алгоритма»
Понятие использование основных требований к алгоритмам нуждаются в уточнениях тогда появляется др понятия которые также будут нуждатся в уточнение и т д Поэтому в теории алгоритмов принят другой подход выбирается конечное число исходных объектов которые объявляются элементарными и все множество объектов строится на основе этих исходных объектов этот подход используется и при уточнение понятия алгоритмов:
1. данные(в качестве данных принимается множество слов конечного алфавита)
2. память (решается вопрос оргонизации памяти)
3. детерминированность (используется блок схемы или словестные описания или др описания механизма реализации алгоритмов)
4. элементарные шаги: фиксируется набор элементарных шагов.
После того как указанные и пункта выполнены получается конкретная алгоритмическая модель, каждая из которых претендует на право считаться формализации понятия алгоритма т.е. модель должна быть универсальной т.е. допускать описание любых алгоритмов Вопрос не приведет ли выбор конкретных средств для получения модели потери общности формализации? Ответ не приведет т к
1. доказана сходимость одних моделей к другим
2. благодаря взаимной сводимости моделей в теория алгоритмов удалось выработать инвариантную к выбору моделей систему понятий позволяющую говорить о свойствах алгоритмов не зависемо от того какая формализация алгоритма выбрана
Эта система понятий основана на понятии вычисления функций т.е функций
для вычисления которой существует алгоритм
Очевидно что с каждым алгоритмом связана функция которую он вычисляет. Верно ли обратное, существует ли для каждой функции существует алг?
исследование проблемы остановления для м.т. показывает что нет. для каких функций существует алгоритм как описать такие алгоритмические эффективно вычисляемые функции исследование в этом направлении начались в 30-е годы тогда и была придумана м.т. и заложена теория рекурсивности функций. в этой теории как и вообще в теории алгоритмов фиктивный и конструктивный подход, основной которой является что все множество исследованных обьектов(функций) строится из конечного числа исходных объектов (некоторого базиса) с помощью простых операций эффективна выполнимость которых вполне достаточна операции над функциями будем называть операторами.
Частичные числовые функции
n-местной функцией будем понимать функцию функцию 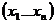 определенную на множестве М которое является подмножеством N к
определенную на множестве М которое является подмножеством N к 
Если  то функция является полностью определенной
то функция является полностью определенной
Пусть есть 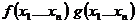
Функции f,g равны если любом наборе 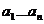 значений аргументов
значений аргументов 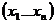 имеет место следующее; если значение f и g определены
имеет место следующее; если значение f и g определены 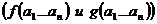 и совпадают или значение обеих функций не определены.
и совпадают или значение обеих функций не определены.
Простейшие функции
Следующие всюдуопределенные функции которые будем использовать в качестве исходных назовем простейшими:
1. функция ноль 0(Х)=0
2. функция следование S(X)=X+1
3. функция выбора аргумента: 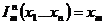
функция выбора аргумента позволяет в частности выполнять формальное введение формальных аргументов
Операторы
1. Операция суперпозиции
2. примитивной рекурсии
3. оператор минимизации
Оператор суперпозиции
пусть имеются частичные функции  зависящие от одного и того же набора аргументов
зависящие от одного и того же набора аргументов  и n – мерная частичная функция g.
и n – мерная частичная функция g.
Суперпозицией функций  называется функция
называется функция  которая является частичной с одной стороны и значение которой на наборе
которая является частичной с одной стороны и значение которой на наборе 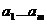 тогда и только тогда когда определены на этом наборе значений функции
тогда и только тогда когда определены на этом наборе значений функции 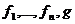 в противном случае велечина на n считается неопределенной.
в противном случае велечина на n считается неопределенной.
Примитивная рекурсия
Случай 1 частичная функция f есть функция одного аргумента.
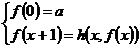 где a=const
где a=const
f(0)=a f(1)=h(0,f(0)),f(2)=h(1,f(1))…..
случай 2 Функция от двух аргументов
f(x,y)
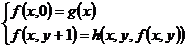
Замечание: в этом случае х играет роль параметра рекурсии ведется по второму аргументу.
Случай 3 (общий) Функция от n аргументов  и y
и y
Заданы частичные функции: 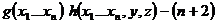

будем говорить что функция 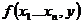 получается из функций g и h применением оператора примитивнрй рекурсии если для любых
получается из функций g и h применением оператора примитивнрй рекурсии если для любых 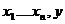 имеет место схема (*) и обозначается это так
имеет место схема (*) и обозначается это так 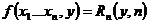
при этом величина 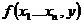 определена т и т т к определены значения функций
определена т и т т к определены значения функций 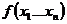 и
и 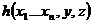 где
где 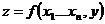
Замечание1 Оператор примитивной рекурсии применим к всюду опред функции g и n дает всюду определенную функцию f
Замечание2 Если значение  не определено при некотором
не определено при некотором 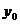 то
то  -так же неопределенно для всех y>y0
-так же неопределенно для всех y>y0
Замечание3 не зависимо от числа переменных функции f рекурсия ведется всегда только по одной переменной а остальные переменные на момент применения схемы играют роль параметров и зафиксированы





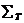
 где α – исходное слово не ленте если м.т. останавливается при исход данных U
где α – исходное слово не ленте если м.т. останавливается при исход данных U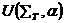 не останавливается если м.т. при исход данных не останавливается.
не останавливается если м.т. при исход данных не останавливается. (истина) если м.т. от α останавливается и
(истина) если м.т. от α останавливается и  (ложь) если Т(α) не останавливает эта проблема остановки.
(ложь) если Т(α) не останавливает эта проблема остановки.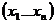 определенную на множестве М которое является подмножеством N к
определенную на множестве М которое является подмножеством N к 
 то функция является полностью определенной
то функция является полностью определенной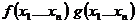
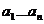 значений аргументов
значений аргументов 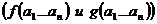 и совпадают или значение обеих функций не определены.
и совпадают или значение обеих функций не определены.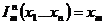
 зависящие от одного и того же набора аргументов
зависящие от одного и того же набора аргументов  и n – мерная частичная функция g.
и n – мерная частичная функция g. которая является частичной с одной стороны и значение которой на наборе
которая является частичной с одной стороны и значение которой на наборе 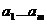 тогда и только тогда когда определены на этом наборе значений функции
тогда и только тогда когда определены на этом наборе значений функции 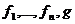 в противном случае велечина на n считается неопределенной.
в противном случае велечина на n считается неопределенной.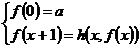 где a=const
где a=const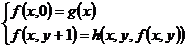
 и y
и y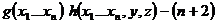

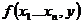 получается из функций g и h применением оператора примитивнрй рекурсии если для любых
получается из функций g и h применением оператора примитивнрй рекурсии если для любых 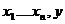 имеет место схема (*) и обозначается это так
имеет место схема (*) и обозначается это так 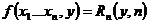
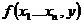 определена т и т т к определены значения функций
определена т и т т к определены значения функций 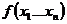 и
и 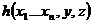 где
где 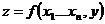
 не определено при некотором
не определено при некотором 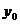 то
то 


