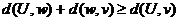Имеет размерность 2м
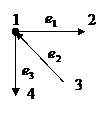
| № ребра
| №№ начабо и конец ребра
|
| 1
| 1,2
|
| 2
| 1,3
|
| 3
| 1,4
|
Список ребер(дуг) орграфоф

| № ребра
| №№ начабо и конец ребра
|
| 1
| 1,2
|
| 2
| 3,1
|
| 3
| 1,4
|
Замечание:
1. список ребер является наибольшее компактным из всех представлений графа т.к. не содержит нулевых элементов в отличии от матричного представления
маршруты, цепи, циклы.
Пусть G=(V,E) неорграф
Маршрутом в графе G называется такая конечная или бесконечная последовательность
Ребер  что каждые соседние два ребра имеют общую инцидетную вершину:
что каждые соседние два ребра имеют общую инцидетную вершину: 
Замечание: одно и тоже ребро не может встречаться в маршруте несколько раз.
Конечный маршрут 
v0,vn- называются кольцевыми вершинами
v0 - начало маршрута
vn – конец маршрута
остальные точки маршрута называется внутренними точками
замечание: одна и та же точка может быть кольцевой и внутренней точкой

Циклический маршрут называется маршрут S в которой v0=vn
Цепью называются не циклические маршрут в котором каждое ребро встречается не более одного раза.
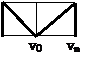
Цикл – это циклич маршрут в котором каждое ребро встречается не более одного раза.

Простая цепь и простой цикл. Простая цепь – если в ней никакая вершина не повторяетя
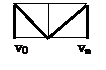
Простым циклом назыв цикл с концом vx в котором вершина v0 не является внутренней (промежуточной) и никакие другие вершины не повторяются
Граф не содержащий циклов называется ациклическим графом
Замечание: маршруты орграов можно рассматривать как с учетом орентации так и без учета, в последнем случае рассматривают маршрут в соотнесенном неорграфе.
Связанный граф.
Связанные компоненты графа.
Пусть G=(V,E) –неорграф
Вершины графа - 
v,w графа G назыв связанным если существует маршрут с концами v и w
v и w – связанные вершины
нетрудно видеть: что если две вершины v, w – связанные то их соединяет простая цепь
Граф G связан если любая его пара вершин х в нем связана
Рассмотрим G=(V,E) – не связанный граф очевидно 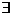 такое разложение множество его вершин на попарно пересекающиеся подмножества
такое разложение множество его вершин на попарно пересекающиеся подмножества 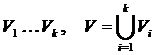 что все вершины в одном подмножестве связаны а вершины из различных подмножеств несвязан тогда граф G разлагается на непересекающиеся связные подграфы называемые связными компонентами графа
что все вершины в одном подмножестве связаны а вершины из различных подмножеств несвязан тогда граф G разлагается на непересекающиеся связные подграфы называемые связными компонентами графа 

Связный ациклический граф называется деревом
 длинна напр количеством в этом маршруте ребер(если некоторое ребро
длинна напр количеством в этом маршруте ребер(если некоторое ребро
повторяется более одного раза то оно учитывается)
Т.1/ Если в графе G равно две вершины имеют нечетную степень то эти вершины связаны.
Док-во:
Используем теорему о том что во всяком графе число вершин нечетной степени четно.
В случае связного графа это очевидно. Рассмотрим случай несвязанного – G U и v – вершины имеющие нечетную степень
Пусть вершина U попала в связную компоненту V1
Т.к. каждая связанная компонента графа тоже есть граф то вторая связная вершина поподает в V1
Чтд.
Расстояние в графе.
G=(V,E); U,v – вершины графа расстояние между U и v в графе G назыв наименьшая длинна простой цепи соеденяющей U и v
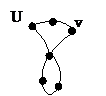
Обознач для расстояния d(U,v)
Для примера d(U,v)=2
Св - ва расстояний
1. 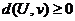 причем d(U,v)=0 тогда и только тогда когда U=v
причем d(U,v)=0 тогда и только тогда когда U=v
2. d(u,v)=d(v,U)
3. 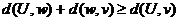
замечание: раст в орграфе можно рассматривать с учетом и без учета орентации





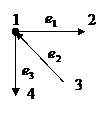

 что каждые соседние два ребра имеют общую инцидетную вершину:
что каждые соседние два ребра имеют общую инцидетную вершину: 


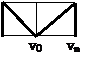

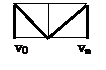

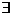 такое разложение множество его вершин на попарно пересекающиеся подмножества
такое разложение множество его вершин на попарно пересекающиеся подмножества 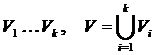 что все вершины в одном подмножестве связаны а вершины из различных подмножеств несвязан тогда граф G разлагается на непересекающиеся связные подграфы называемые связными компонентами графа
что все вершины в одном подмножестве связаны а вершины из различных подмножеств несвязан тогда граф G разлагается на непересекающиеся связные подграфы называемые связными компонентами графа 

 длинна напр количеством в этом маршруте ребер(если некоторое ребро
длинна напр количеством в этом маршруте ребер(если некоторое ребро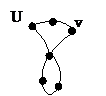
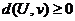 причем d(U,v)=0 тогда и только тогда когда U=v
причем d(U,v)=0 тогда и только тогда когда U=v