Разностные схемы при (не)симметричных аппроксимациях не обладают свойствами монотонности. Поэтому при расчете разрывных течениях происходят осцилляции на разрывах и надо проводить сглаживание.
Так как система уравнений газовой динамики обладает свойством гиперболичности, то она невырожденными преобразованиями может быть приведена к симметричному виду.
 .
.
1) Система уравнений газовой динамики является однородной.
 .
.
Возьмем матрицу  диагонального вида
диагонального вида

Система Маккормака в этом случае:
 ,
,

где


1.7.2. Схемы для одномерных уравнений в недивергентной форме
Уравнения газовой динамики и уравнения Навье-Стокса могут использовать несколько форм представления:
1. Дивергентная.
2. Недивергентная.
3. Предельная дивергентная.
Мы рассмотрели различные виды разностных схем в дивергентной форме. Было подчеркнуто, что в результате линеаризации этих уравнений получены сложные матрицы B и С. Поэтому предлагается выбор исходного вектора переменных 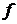 в эквивалентной форме, благодаря которому можно получить более экономичную разностную схему. Как правило, для уравнений газовой динамики
в эквивалентной форме, благодаря которому можно получить более экономичную разностную схему. Как правило, для уравнений газовой динамики 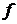 выбирается в переменных
выбирается в переменных  , что позволяет решать независимо уравнение неразрывности относительно остальных уравнений системы. Для системы уравнений Навье-Стокса
, что позволяет решать независимо уравнение неразрывности относительно остальных уравнений системы. Для системы уравнений Навье-Стокса 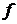 выбирается в переменных
выбирается в переменных  , что позволяет аккуратно записывать граничные условия.
, что позволяет аккуратно записывать граничные условия.
Уравнения газовой динамики:
 . (1)
. (1)
 .
.
Уравнения Навье-Стокса:
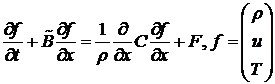 . (2)
. (2)
 .
.
 .
.
Для решения этих уравнений предлагается следующая разностная схема:
 (3)
(3)
Схема (3) аппроксимирует (1) и (2) с  , где
, где 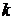 зависит от порядка разностной производной. Для уравнений газовой динамики
зависит от порядка разностной производной. Для уравнений газовой динамики
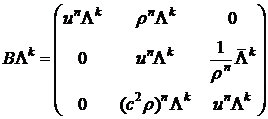 .
.
и для уравнений Навье- стокса

– для получения безусловно устойчивой схемы.
Из вида матриц  и (3) видно, что для нахождения решения (2) используется векторные прогонки, а для решения (1) используются векторная прогонка для нахождения координат
и (3) видно, что для нахождения решения (2) используется векторные прогонки, а для решения (1) используются векторная прогонка для нахождения координат  и
и 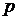 , а затем можно пересчитать
, а затем можно пересчитать  из уравнения неразрывности методом сквозного счета.
из уравнения неразрывности методом сквозного счета.
Схема (3) безусловно устойчива при  .
.
Выведем условие устойчивости для схемы (3) в случае решения системы газовой динамики (1), выбирая симметричную аппроксимацию пространственных переменных (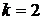 ).
).





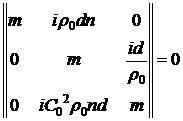 .
.

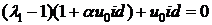 .
.
 .
.

Схема безусловно устойчива при  .
.
Для получения схем, реализующихся скалярными прогонками, можно какие-то из слагаемых, например с 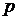 , аппроксимировать на нижнем временном слое, но при этом ухудшается условие устойчивости – схемы становятся условно устойчивыми и условие устойчивости зависит от числа Маха:
, аппроксимировать на нижнем временном слое, но при этом ухудшается условие устойчивости – схемы становятся условно устойчивыми и условие устойчивости зависит от числа Маха:
 – число Маха.
– число Маха.
Например, система уравнений газовой динамики имеет вид

В качестве модельной, выберем систему уравнений газовой динамики в переменных  :
:
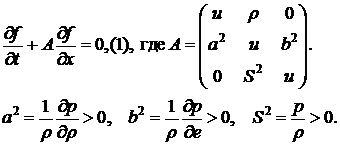
Система (1) недивергентного вида и давление исключено из этой системы с помощью уравнения состояния: 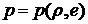
 .
.
Используем расщепление дифференциального оператора по физическим процессам:

Оператор 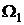 учитывает конвективные слагаемые. Оператор
учитывает конвективные слагаемые. Оператор  учитывает слагаемые при градиенте давления в уравнении скорости и слагаемые при градиенте скорости в уравнении неразрывности и движения.
учитывает слагаемые при градиенте давления в уравнении скорости и слагаемые при градиенте скорости в уравнении неразрывности и движения.
Уравнение (1) после расщепления примет вид:

 (2)
(2)
(2) – схема с весами по пространству, является схемой слабой аппроксимации.
Перепишем схему (2), выделяя стабилизирующие операторы:

Выразим в целых временных шагах. Для этого первое уравнение умножим слева 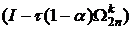 а второе на
а второе на  и сложим оба уравнения:
и сложим оба уравнения:



Операторы  и
и 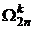 в общем случае неперестановочные. В частном случае, когда
в общем случае неперестановочные. В частном случае, когда  и когда их можно убрать, эти операторы можно менять местами.
и когда их можно убрать, эти операторы можно менять местами.
Таким образом схема (2) имеет первый порядок по времени и 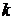 -й по пространству в общем нелинейном случае.
-й по пространству в общем нелинейном случае.
Если  и в случае уравнения с постоянными коэффициентами оно имеет 2-й порядок аппроксимации по времени.
и в случае уравнения с постоянными коэффициентами оно имеет 2-й порядок аппроксимации по времени.
1.7.3. Реализация схемы на дробных шагах
Рассматривается система (2).
На первом дробном шаге вид оператора 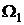 диагональный, поэтому вектор потока для каждой своей координаты находится независимо от других координат.
диагональный, поэтому вектор потока для каждой своей координаты находится независимо от других координат.
1) если взять  , то это неявная схема бегущего счета.
, то это неявная схема бегущего счета.

Если  , то счет слева направо, если
, то счет слева направо, если  – наоборот.
– наоборот.
Если знак скорости меняется, то – 3-х точечная прогонка.
 ,
,
где  .
.
Прогонка хорошо обусловлена при 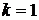 .
.
При 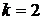 прогонка обусловлена при
прогонка обусловлена при  .
.
В случае плохой обусловленности  решаем методом немонотонной прогонки
решаем методом немонотонной прогонки  .
.
2)  .
.

Вводим фиктивный слой.
Можно использовать экстраполяционные формулы
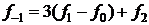 ,
,
или можно изменить аппроксимацию на границе на симметричную. В этом случае нарушается однородность разностной схемы.
На втором дробном шаге схемы (2) решается следующее уравнение:

В уравнении движения слагаемые с давлением аппроксимируются симметричным разностным оператором.
Исключаем  и
и  из последнего уравнения. Получаем разностные уравнения для значения скорости на
из последнего уравнения. Получаем разностные уравнения для значения скорости на  временном слое. Это уравнение решается трехточечной скалярной прогонкой. Затем из первых двух уравнений находятся плотность и энергия.
временном слое. Это уравнение решается трехточечной скалярной прогонкой. Затем из первых двух уравнений находятся плотность и энергия.
Рассматривается схема (2):

Проверим устойчивость в линейном случае для схемы с замороженными коэффициентами.


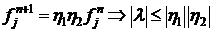 .
.
На первом дробном шаге:

 .
.
Заменим для удобства  .
.
Выпишем определитель.
Если  , то определитель имеет вид:
, то определитель имеет вид:
 .
.



 при
при  .
.
Вместо  можно взять
можно взять  , так как эти коэффициенты не меняются.
, так как эти коэффициенты не меняются.
На втором дробном шаге сразу выпишем корни характеристического уравнения (задействована матрица  , которая не является диагональной).
, которая не является диагональной).
 ,
,
где  – скорость звука:
– скорость звука:
 .
.
 , где
, где 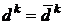 при
при  ;
;  при
при  .
.
 , при
, при  .
.
1.7.4. Уравнения газовой динамики и Навье-Стокса в переменных, полученных комбинацией газодинамических переменных
При построении газодинамических схем в качестве переменных могут быть выбраны различные комбинации газодинамических параметров.
Один из вариантов:  .
.
Выбор таких переменных обусловлен следующим:
1. Уравнения газовой динамики и Навье-Стокса в этих переменных имеют более простую форму и просты в реализации.
2. Уравнения неразрывности и движения записываются в дивергентной форме. А это приводит к ускорению сходимости схемы к стационарному решению.
3. Уравнение энергии может быть использовано как и в недивергентной, так и в дивергентной форме. При использовании уравнения энергии в дивергентной форме мы получаем полностью консервативные схемы (т.е выполняются все законы сохранения).
Рассмотрим систему:
 , (1)
, (1)
где для случая системы газовой динамики:
 ,
,
а для случая системы уравнений Навье-Стокса:
 .
.
Здесь  .
.
Рассмотрим разностную схему для системы уравнений газовой динамики:
 . (2)
. (2)
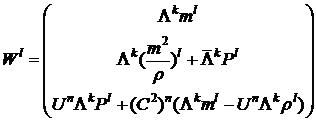 .
.
Схема нелинейна относительно  . Проводим линеаризацию:
. Проводим линеаризацию:
 .
.
(2)  , где
, где  .
.
Для того, чтобы получить оператор  , который удовлетворяет следующим требованиям:
, который удовлетворяет следующим требованиям:
1) Схема должна остаться безусловно устойчивой.
2) Реализована скалярными прогонками.
3) Требовать минимального числа операций.
Матрицу  можно расщепить четырьмя способами, но для выполнения третьего условия,
можно расщепить четырьмя способами, но для выполнения третьего условия,  расщепляем так:
расщепляем так:
 расщепляется на:
расщепляется на:
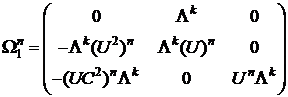 .
.
 .
.
Окончательно имеем:
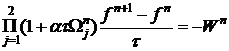 .
.
Данная схема может быть реализована с помощью дробных шагов. Можно использовать метод «стабилизирующей поправки».
 (4)
(4)
Реализация схемы (2) в зависимости от расщепляющих операторов следующая:
1) На первом дробном шаге матрица нижнетреугольная ( ), поэтому переменные находятся так: сначала
), поэтому переменные находятся так: сначала  . А затем независимо друг от друга находят
. А затем независимо друг от друга находят  и
и  .
.
2) На втором дробном шаге получили систему:

Из последнего уравнения выражается  и подставляем во второе. Получаем уравнение, которое решается скалярными прогонками. А затем пересчитываются первое и третье уравнения.
и подставляем во второе. Получаем уравнение, которое решается скалярными прогонками. А затем пересчитываются первое и третье уравнения.
В качестве уравнения энергии выбираем уравнение в дивергентном виде:
 .
.
 ,
,
где  .
.
 – уравнение связи.
– уравнение связи.
Для решения системы используем следующую схему с весами, которая аппроксимирует исходную систему с  , но является нелинейной относительного верхнего временного слоя:
, но является нелинейной относительного верхнего временного слоя:
 .
.
Для получения линейной системы проводим линеаризацию, используя следующие разложения в ряд Тейлора:
 .
.
 .
.
 .
.
 .
.
Подставляем эти выражения, получаем линеаризованную схему:
 . (3)
. (3)
Эта система может быть решена векторными прогонками. Для того, чтобы получить систему, реализующуюся скалярными прогонками, проводим расщепление и рассматриваем схему с факторизованным стабилизирующим оператором или рассматриваем схему в дробных шагах, эквивалентную ей.
 . (4)
. (4)
В этом случае схема (3) имеет вид:
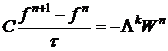 ,
,
где  .
.
и порядок аппроксимации 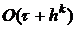 . Схема реализуется в дробных шагах.
. Схема реализуется в дробных шагах.
 (5)
(5)
 .
.
На первом дробном шаге:

На втором дробном шаге:

Расщепление матрицы  на матрицы
на матрицы  и
и 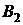 неоднозначно. Можно выбрать такое:
неоднозначно. Можно выбрать такое:
 .
.
Схемы при таком расщеплении на каждом дробном шаге реализуются по схемам бегущего счета. Но схема становится условно устойчивой.
1.7.5. Схемы с несогласованным стабилизирующим оператором
При аппроксимации частных производных, вида  , несимметричными разностными операторами
, несимметричными разностными операторами 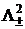 , получаются схемы, которые реализуются пятиточечными прогонками. Для получения стационарного решения методом установления можно использовать схемы, в которых стабилизирующий оператор аппроксимируется одним порядком, а правая часть другим. При установлении аппроксимация разностной схемы выбирается по аппроксимации правой части. Это позволяет строить разностные схемы, которые реализуются трехточечными прогонками.
, получаются схемы, которые реализуются пятиточечными прогонками. Для получения стационарного решения методом установления можно использовать схемы, в которых стабилизирующий оператор аппроксимируется одним порядком, а правая часть другим. При установлении аппроксимация разностной схемы выбирается по аппроксимации правой части. Это позволяет строить разностные схемы, которые реализуются трехточечными прогонками.
Рассматривается недивергентная система уравнений Навье-Стокса, которая аппроксимируется факторизованной схемой.
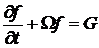 . (1)
. (1)
 . (2)
. (2)
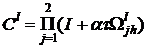 ,
, 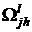 – расщепляющий оператор.
– расщепляющий оператор.
Схема (2) решается  -точечными прогонками и погрешность ее аппроксимации
-точечными прогонками и погрешность ее аппроксимации
 ,
,
 – порядок аппроксимации стабилизирующего оператора.
– порядок аппроксимации стабилизирующего оператора.
При установлении, порядок аппроксимации может быть больше, чем у стабилизирующего оператора.
Оператор 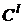 называется согласованным, если
называется согласованным, если  , несогласованным, если
, несогласованным, если  .
.
Рассмотрим схему с несогласованным оператором  . Эта схема по-прежнему остается безусловно устойчивой, но запас устойчивости уменьшился.
. Эта схема по-прежнему остается безусловно устойчивой, но запас устойчивости уменьшился.
Характеристическое уравнение имеет вид:

 .
.
 ,
, 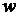 – волновое число.
– волновое число.
 .
.
Два других корня находят в предельном случае.
 : а)
: а)  – гиперзвук,
– гиперзвук,  .
.
б)  – медленные течения,
– медленные течения, 
 ,
,
где
 .
.
1) Таким образом, схема (2) безусловно устойчива при  в случае согласованного стабилизирующего оператора, и при
в случае согласованного стабилизирующего оператора, и при  в случае несогласованного стабилизирующего оператора.
в случае несогласованного стабилизирующего оператора.
2) В многомерном случае схема приближенной факторизации с несогласованным стабилизирующим оператором становится условно устойчивой.
1.7.6. Схемы для решения стационарных задач
При решении стационарных задач уравнений газовой динамики и Навье-Стокса используется два подхода:
1) Непосредственное интегрирование системы стационарных уравнений.
2) Интегрирование некоторой аппроксимирующей системы, решение которой стремится к решению исходной стационарной системы.
Использование первого подхода не представляет особых трудностей для решения одномерных систем уравнений, т.к. одномерные системы стационарных уравнений являются системой ОДУ, хотя и нелинейные. В многомерном случае получается система уравнений в частных производных, тип которых зависит от режима течений. Как правило, для уравнений газовой динамики при сверхзвуковом течении - система эллиптическая, для параболизованных систем Навье-Стокса – система параболического или эллиптического типа.
Решение уравнений, особенно эллиптического типа, представляет значительные трудности. Поэтому экономичнее использовать второй подход для решения систем (стационарных), основанных на итерационных методах. В уравнения добавляют итерационное слагаемое, временной параметр – итерация, и методом установления решается система уравнений, которая сходится к исходной системе.
Такой метод хорош тем, что он используется для любого типа течений.
Рассмотрим этот метод на примере простейших модельных уравнений. Рассмотрим слагаемые, описывающие диффузию:
 . (1)
. (1)
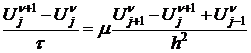 . ???? (2)
. ???? (2)
 – номер итерации.
– номер итерации.
В результате установления должно получиться:
 .
.
 .
.
Итерационная схема (2) аппроксимирует (1) уже при установлении  , а на одной итерации (2) аппроксимирует совсем не уравнение (1).
, а на одной итерации (2) аппроксимирует совсем не уравнение (1).
К числителю дроби, стоящей в правой части (2) прибавим  и отнимем
и отнимем  . Получим:
. Получим:
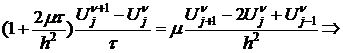
На каждом шаге схема (2) аппроксимирует задачу:
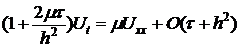 .
.
Схема (2) безусловно устойчива. Устойчивость исследуем методом гармоник.
 .
.
Получим:
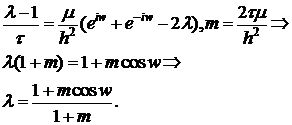
 , так как
, так как  .
.
Таким образом, схема (2) действительно безусловно устойчива.
Расчет по схеме (2) тоже несложный:
 .
.
Можно строить итерационные схемы, которые также являются безусловно устойчивыми, например:
 . (3)
. (3)
(3) считается по неявной схеме бегущего счета.
В работах Саульева предложены схемы для решения уравнения теплопроводности с использованием расщепления, например:
 (4)
(4)
Схема Саульева безусловно устойчива, аппроксимирует со вторым порядком.
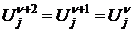 – при установлении, что можно проверить, исключив дробные шаги:
– при установлении, что можно проверить, исключив дробные шаги:

 .
.
Используя, что
 ,
,
получим

– аппроксимирует со вторым порядком по времени.
Каждое уравнение реализуется по схеме бегущего счета: первое уравнение – справа налево, а второе наоборот.
Рассмотрим уравнение:
 . (1.1)
. (1.1)
Добавляем итерационное слагаемое:
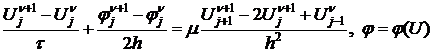 .
.
Эта система аппроксимирует (1.1) с  .
.
Рассмотрим нестационарную систему уравнений:
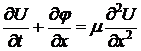 .
.
Если вектор потока расщепить:  , то можно строить монотонные схемы.
, то можно строить монотонные схемы.
 .
.
Получим многошаговую итерационную схему:

Здесь используется условие монотонности и схема Саульева.
После линеаризации векторов  (по формуле Тейлора):
(по формуле Тейлора):

и использования этого разложения в исходной схеме, получаем схему, которая реализуется с помощью бегущего счета:
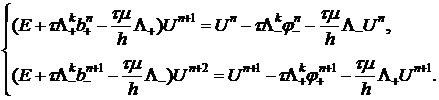
Первое уравнение – бегущий счет справа налево, второе уравнение – наоборот.
1.7.7. Схемы для многомерных уравнений
Для численного решения многомерных уравнений, построение разностной схемы усложняется (если использовать явные разностные схемы, то, как правило, ухудшается условие устойчивости), например, для уравнения переноса:
– в одномерном случае:
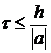 ,
,
– в двухмерном случае:
 .
.
 .
.
Хотя реализация схем сильно не усложняется.
Хуже для неявных разностных схем. Схемы в этом случае становятся неэкономичными: или становятся условно устойчивыми, или реализуются матричными прогонками.
На основе схем расщепления можно построить экономичную разностную схему.
Для многомерных систем уравнений строится цепочка задач меньшей размерности, а затем эта цепочка исследуется.
Заключение по модулю
Второй модуль учебника носит прикладной характер. Основные методы теории разностных схем апробируются на задачах механики. Показано, как применяя разностный подход можно численно исследовать реальные физические модели.
При изложении материала данного модуля использовались разделы вычислительной механики, в частности аэродинамики, а также раздел механики жидкости и газа.
Вопросы для самоконтроля
1) Физико-математическая постановка задачи.
2) Безразмерные величины. Критерии подобия.
3) Упрощенные модели системы уравнений Навье- Стокса..
4) Схема Лакса первого и второго порядка аппроксимации.
5) Разностная схема с весами для линейного и нелинейного уравнений.
6) Дисперсионные и диссипативные свойства разностных схем.
7) Схемы приближенной факторизации.
8) Монотонные разностные схемы.
9) Схемы с несогласованным стабилизирующим оператором.
10) Схемы для системы уравнений газовой динамики.
1.9. Проектное задание
Контрольная работа №1
1. Исследовать порядок аппроксимации и устойчивость следующих разностных схем линейных одномерных уравнений газовой динамики:
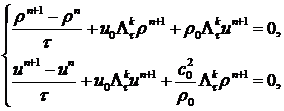
где 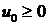 и
и  .
.
Ответ: условно-устойчивая.
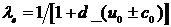 ,
, 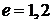 ,
,
где 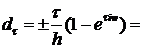
Контрольная работа №2
1. Исследовать порядок аппроксимации и устойчивость следующих разностных схем линейных одномерных уравнений газовой динамики:

где  и
и  .
.
Ответ: безусловно-устойчивая.
 ,
, 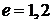 ,
,
Контрольная работа №3
1. Исследовать порядок аппроксимации и устойчивость следующих разностных схем линейных одномерных уравнений газовой динамики:
где 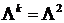 и
и  – сопряженный оператор.
– сопряженный оператор.
Ответ: условно-устойчивая.
 ,
,
при 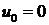 схема устойчивая, если
схема устойчивая, если  .
.
Контрольная работа №4
1. Исследовать порядок аппроксимации и устойчивость следующих разностных схем линейных одномерных уравнений газовой динамики:

где  и
и  – сопряженный оператор.
– сопряженный оператор.
Ответ: условно-устойчивая.
Безусловно-устойчивая лишь для сверхзвуковых течений 
Тест рубежного контроля
1) Вопрос: какое течение жидкости описывается матрицей инерциальных сил:
1. Вязкое 2. Турбулентное 3. Слабомолекулярное
2) Вопрос: от числа Маха зависит:
1. Скорость течения жидкости
2. Физико – математические характеристики потока
3. Оба первых два случая
3) Вопрос: матрица Якоби используется для:
1. Нахождения решения системы уравнений
2. Преобразования системы уравнений в недивергентную форму
3. Обезразмеривания переменных
4) Вопрос: в асимптотическом разложении уравнений Навье – Стокса по малому параметру первым приближением содержащем малый параметр в нулевой степени является:
1. Система уравнений вязкого ударного газа
2. Система обобщенных уравнений Прандтля
3. Система уравнений погранслоя
5) Вопрос: достаточным условием корректности и устойчивости метода прогонки является:
1. Не отрицательность коэффициентов матрицы
2. Условие диагонального преобладания
3. Не обращение в ноль прогоночных коэффициентов
6) Вопрос: построить схемы повышенного порядка аппроксимации можно:
1. С помощью многосеточных методов
2. С помощью выбора специального оператора усреднения
3. Используя оба метода
7) Вопрос: операторы  и
и 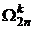 являются перестановочными если
являются перестановочными если
1. Они равны
2. 
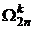 =
= 
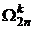
3. 
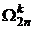 = 1
= 1
8) Вопрос: процесс расщепления схемы необходим для:
1. Для повышения порядка аппроксимации.
2. Для построения эффективного алгоритма.
3. Для улучшения устойчивости схемы.
9) Вопрос: При линеаризации разностной схемы получается:
1. Схема повышенного порядка аппроксимации.
2. Монотонная схема.
3. Схема реализующаяся методом прогонки.
10) Вопрос: Какие схемы называются безусловно устойчивыми:
1. Схемы расщепления.
2. Схемы у которых правая часть более высокого порядка
аппроксимации.
3. Схемы у которых шаг по времени не зависит от шага по
пространству.
Бланк правильных ответов
| № вопрс. / № отв.
| 1
| 2
| 3
|
| 1
|
|
| *
|
| 2
|
|
| *
|
| 3
|
| *
|
|
| 4
|
|
| *
|
| 5
|
| *
|
|
| 6
| |
| *
|
| 7
| | *
|
|
| 8
| | *
|
|
| 9
| |
| *
|
| 10
| |
| *
|
Оценка: за девять или десять правильных ответов – отлично.
За семь правильных ответов - хорошо.
За шесть правильных ответов – удовлетворительно.
Остальное число ответов оценивается неудовлетворительно



 .
. .
. диагонального вида
диагонального вида
 ,
,


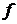 в эквивалентной форме, благодаря которому можно получить более экономичную разностную схему. Как правило, для уравнений газовой динамики
в эквивалентной форме, благодаря которому можно получить более экономичную разностную схему. Как правило, для уравнений газовой динамики  , что позволяет решать независимо уравнение неразрывности относительно остальных уравнений системы. Для системы уравнений Навье-Стокса
, что позволяет решать независимо уравнение неразрывности относительно остальных уравнений системы. Для системы уравнений Навье-Стокса  , что позволяет аккуратно записывать граничные условия.
, что позволяет аккуратно записывать граничные условия. . (1)
. (1) .
.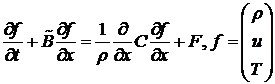 . (2)
. (2) .
. .
. (3)
(3) , где
, где 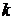 зависит от порядка разностной производной. Для уравнений газовой динамики
зависит от порядка разностной производной. Для уравнений газовой динамики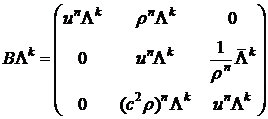 .
.
 и (3) видно, что для нахождения решения (2) используется векторные прогонки, а для решения (1) используются векторная прогонка для нахождения координат
и (3) видно, что для нахождения решения (2) используется векторные прогонки, а для решения (1) используются векторная прогонка для нахождения координат  и
и 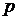 , а затем можно пересчитать
, а затем можно пересчитать  из уравнения неразрывности методом сквозного счета.
из уравнения неразрывности методом сквозного счета. .
.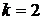 ).
).




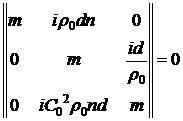 .
.
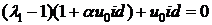 .
. .
.
 – число Маха.
– число Маха.
 :
: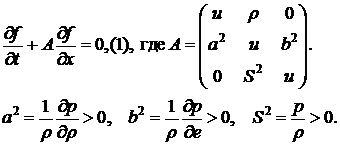
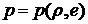
 .
.
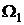 учитывает конвективные слагаемые. Оператор
учитывает конвективные слагаемые. Оператор  учитывает слагаемые при градиенте давления в уравнении скорости и слагаемые при градиенте скорости в уравнении неразрывности и движения.
учитывает слагаемые при градиенте давления в уравнении скорости и слагаемые при градиенте скорости в уравнении неразрывности и движения.
 (2)
(2)
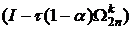 а второе на
а второе на  и сложим оба уравнения:
и сложим оба уравнения:


 и
и 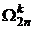 в общем случае неперестановочные. В частном случае, когда
в общем случае неперестановочные. В частном случае, когда  и когда их можно убрать, эти операторы можно менять местами.
и когда их можно убрать, эти операторы можно менять местами. и в случае уравнения с постоянными коэффициентами оно имеет 2-й порядок аппроксимации по времени.
и в случае уравнения с постоянными коэффициентами оно имеет 2-й порядок аппроксимации по времени. , то это неявная схема бегущего счета.
, то это неявная схема бегущего счета.
 , то счет слева направо, если
, то счет слева направо, если  – наоборот.
– наоборот. ,
, .
.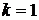 .
. .
. решаем методом немонотонной прогонки
решаем методом немонотонной прогонки  .
. .
.
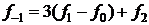 ,
,
 и
и  из последнего уравнения. Получаем разностные уравнения для значения скорости на
из последнего уравнения. Получаем разностные уравнения для значения скорости на  временном слое. Это уравнение решается трехточечной скалярной прогонкой. Затем из первых двух уравнений находятся плотность и энергия.
временном слое. Это уравнение решается трехточечной скалярной прогонкой. Затем из первых двух уравнений находятся плотность и энергия.


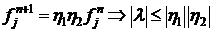 .
.
 .
. .
. , то определитель имеет вид:
, то определитель имеет вид: .
.


 при
при  можно взять
можно взять  , так как эти коэффициенты не меняются.
, так как эти коэффициенты не меняются. , которая не является диагональной).
, которая не является диагональной). ,
, – скорость звука:
– скорость звука: .
. , где
, где 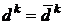 при
при  при
при  .
. , при
, при  .
. , (1)
, (1) ,
, .
. .
. . (2)
. (2)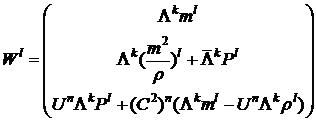 .
. . Проводим линеаризацию:
. Проводим линеаризацию: .
. , где
, где  .
. , который удовлетворяет следующим требованиям:
, который удовлетворяет следующим требованиям: можно расщепить четырьмя способами, но для выполнения третьего условия,
можно расщепить четырьмя способами, но для выполнения третьего условия,  расщепляется на:
расщепляется на: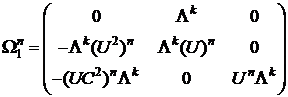 .
. .
.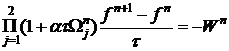 .
. (4)
(4) ), поэтому переменные находятся так: сначала
), поэтому переменные находятся так: сначала  . А затем независимо друг от друга находят
. А затем независимо друг от друга находят  и
и 
 .
. ,
, .
. – уравнение связи.
– уравнение связи. .
. .
. .
. .
. .
. . (3)
. (3) . (4)
. (4)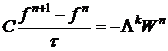 ,
, .
.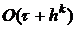 . Схема реализуется в дробных шагах.
. Схема реализуется в дробных шагах. (5)
(5) .
.

 на матрицы
на матрицы  и
и 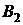 неоднозначно. Можно выбрать такое:
неоднозначно. Можно выбрать такое: .
. , несимметричными разностными операторами
, несимметричными разностными операторами 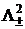 , получаются схемы, которые реализуются пятиточечными прогонками. Для получения стационарного решения методом установления можно использовать схемы, в которых стабилизирующий оператор аппроксимируется одним порядком, а правая часть другим. При установлении аппроксимация разностной схемы выбирается по аппроксимации правой части. Это позволяет строить разностные схемы, которые реализуются трехточечными прогонками.
, получаются схемы, которые реализуются пятиточечными прогонками. Для получения стационарного решения методом установления можно использовать схемы, в которых стабилизирующий оператор аппроксимируется одним порядком, а правая часть другим. При установлении аппроксимация разностной схемы выбирается по аппроксимации правой части. Это позволяет строить разностные схемы, которые реализуются трехточечными прогонками.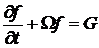 . (1)
. (1) . (2)
. (2)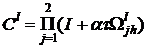 ,
, 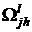 – расщепляющий оператор.
– расщепляющий оператор. -точечными прогонками и погрешность ее аппроксимации
-точечными прогонками и погрешность ее аппроксимации ,
, – порядок аппроксимации стабилизирующего оператора.
– порядок аппроксимации стабилизирующего оператора.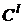 называется согласованным, если
называется согласованным, если  , несогласованным, если
, несогласованным, если  .
. . Эта схема по-прежнему остается безусловно устойчивой, но запас устойчивости уменьшился.
. Эта схема по-прежнему остается безусловно устойчивой, но запас устойчивости уменьшился.
 .
. ,
,  – волновое число.
– волновое число. .
. : а)
: а)  – гиперзвук,
– гиперзвук,  .
. – медленные течения,
– медленные течения, 
 ,
, .
. в случае несогласованного стабилизирующего оператора.
в случае несогласованного стабилизирующего оператора. . (1)
. (1)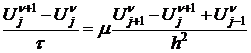 . ???? (2)
. ???? (2) – номер итерации.
– номер итерации. .
. .
. , а на одной итерации (2) аппроксимирует совсем не уравнение (1).
, а на одной итерации (2) аппроксимирует совсем не уравнение (1). и отнимем
и отнимем 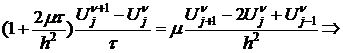
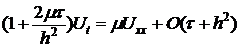 .
. .
.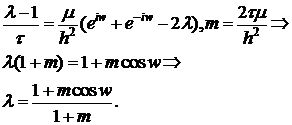
 , так как
, так как  .
. .
. . (3)
. (3) (4)
(4)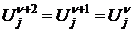 – при установлении, что можно проверить, исключив дробные шаги:
– при установлении, что можно проверить, исключив дробные шаги:
 .
. ,
,
 . (1.1)
. (1.1)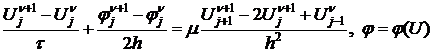 .
.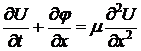 .
. , то можно строить монотонные схемы.
, то можно строить монотонные схемы. .
.
 (по формуле Тейлора):
(по формуле Тейлора):
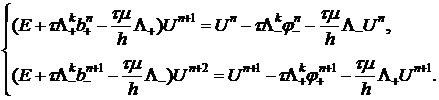
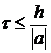 ,
, .
. .
.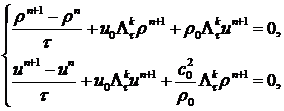
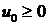 и
и  .
.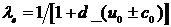 ,
, 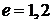 ,
,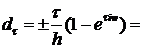

 и
и  ,
, 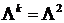 и
и  – сопряженный оператор.
– сопряженный оператор. ,
,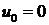 схема устойчивая, если
схема устойчивая, если  .
.
 и
и 



