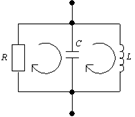
Условие резонанса:
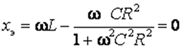
Настройка связанных контуров:
При желании передать во второй контур максимальную энергию, обеспечивающую и максимальны ток в нем, прибегают к настройке системы связанных контуров. Для того чтобы получить самый большой ток во втором контуре, необходимо выполнить два условия: с одной стороны, обеспечить равенство Х1э=0, а с другой, -r1=Rвн Первое условие может быть выполнено двумя способами: 1) настройкой системы (при наличии определенной связи между контурами) на частоту генератора изменением параметров только одного из контуров; 2) настройкой на частоту генератора сначала первого контура при разомкнутом втором, а затем подключением и настройкой второго контура при достаточно слабой связи между контурами, чтобы ослабить взаимное влияние.
Вопрос№ 60. Виды резонансов в связанных системах. Критическая связь.
Вопрос № 61. Понятие о несинусоидальных (негармонических) токах и напряжениях. Возникновение несинусоидальных токов. Понятие о нелинейных элементах. Сложение синусоид, имеющих разные частоты.
Цепями периодического несинусоидального тока называются цепи токи в ветвях которых или напряжения на ветвях которых носят несинусоидальный периодический характер. Причинами возникновения в электрических цепях несинсоидальных периодических токов являются:
1.Несовершенство (неидеальность) источников синусоидальных напряжений и токов.
2. Наличие в ветвях эл. цепей генераторов напряжений и токов специальной формы (прямоугольной, пилообразной, трапециедальной и т.п.)
3. Наличие нелинейных элементов в ветвях эл. цепей.
Возникновение несинусоидальных токов:
Условие возникновения: наличие замкнутой цепи из различных проводников, причем, по крайней мере, один должен быть проводником второго класса и соприкасаться с различными проводниками первого класса
Понятие о нелинейных элементах:
Нелинейными элементами в электрических цепях называют такие элементы, у которых связь между протекающим через них током и напряжением на них не является пропорциональной зависимостью. Для обычного резистора связь между током I и напряжением U имеет вид U=IR, где R – сопротивление резистора, которое есть константа и не зависит от приложенного напряжения.
Сложение синусоид, имеющих разные частоты:
При сложении двух гармонических колебаний разной частоты, происходящих в одном направлении, возникает негармоническое колебание.
Вопрос №62. Выражение сложной периодической кривой с помощью тригонометрического ряда (ряда Фурье). Постоянная составляющая, основная и высшие гармоники. Симметричные и несимметричные кривые. Разложение переодических кривых на гармоники. Понятие о спектрах.
Обычно анализ цепей переменного тока проводится в предположении, что действующие в них ЭДС и токи имеют синусоидальную форму. В большинстве случаев такое предположение оправдано, однако, на самом деле форма токов и напряжений в той или иной степени всегда несинусоидальна.
Искажение ЭДС и токов может возникать вследствие конструктивных особенностей генераторов переменного тока, приводящих к тому, что создаваемая ими ЭДС несинусоидальна, либо вследствие нелинейности элементов электрической цепи. Причем для появления искажений достаточно наличия в цепи только одного нелинейного элемента. Чаще всего обе эти причины присутствуют одновременно, но в зависимости от степени выраженности их воздействия на цепь пренебрегают одной из них или обеими сразу.
Из курса математики известно, что любую несинусоидальную периодическую функцию F(w t) удовлетворяющую условиям Дирихле, т.е. имеющую за полный период конечное число максимумов, минимумов и разрывов первого рода, можно представить в виде ряда Фурье
F(wt) = A0 + A1sin(wt+y 1) + A2sin(2wt+y 2) +ј + Aksin(kwt+yk)+ј = A0 + B1sinwt + B2sin2wt +ј + Bksinkwt+ј + C1coswt + C2cos2wt +ј + Ckcoskwt +ј = A0+a1+a2+ј + ak+ј (1), где

Первый член ряда A0 называется постоянной составляющей или нулевой гармоникой. Второй член A1sin(wt+y 1) имеет частоту равную частоте функции F(wt) и называется первой или основной гармонической составляющей (коротко - гармоникой). Остальные члены ряда вида Aksin(kwt+y k) имеют частоты в целое число раз k больше частоты основной гармоники и называются высшими гармоническим составляющими или гармониками. Каждая высшая гармоника в отдельности именуется по номеру k, т.е. вторая гармоника, третья гармоника и т.д.
Из выражения (1) следует, что каждую гармонику ряда Фурье можно представить в виде двух составляющих - синусной Bksinkwt и косинусной Ckcoskwt. Амплитуды этих составляющих Bk и Ck называются коэффициентами ряда Фурье.
Разложение в ряд Фурье всегда однозначно в отношении постоянной составляющей, а также амплитуд и частот гармонических составляющих. В то же время, начальные фазы гармоник изменяются при изменении момента времени, принятого за начало отсчета. Таким образом, ряд Фурье можно определить, задав номера, амплитуды и начальные фазы гармоник или номера и амплитуды синусной и косинусной составляющих гармоник. Совокупность амплитуд Ak и начальных фаз y k называются соответственно амплитудным и фазовым частотными спектрами, а совокупность коэффициентов Bk и Ck - частотным спектром функции. Спектры функций удобно изображать отрезками прямых линий, пропорциональных соответствующим величинам.
Периодические функции, используемые в электротехнике, чаще всего имеют симметрию. Одни из них симметричны относительно оси абсцисс, другие – относительно оси ординат или начала координат.

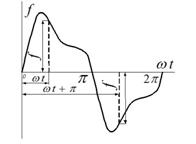
График функции, симметричной относительно оси абсцисс.
При симметрии относительно оси абсцисс значения функции повторяются с обратным знаком через половину периода, поэтому кривая второго полупериода, сдвинутая влево на π, является зеркальным отображением кривой первого полупериода.
В составе тригонометрического ряда функции, подчиняющейся условию, отсутствуют постоянная составляющая и четные гармоники. В этом нетрудно убедиться, если записать ряды вида, для функций ƒ(ωt) и ƒ(ωt+π):
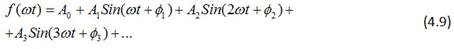
Функция ƒ(ωt+π) отличается от ƒ(ωt) тем, что все нечетные гармоники имеют отрицательный знак:
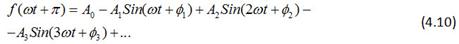
Согласно условию (4.8) ƒ(ωt)+ƒ(ωt+π)=0 Тогда
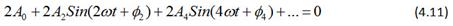
При любом значении ωt это равенство возможно, если A0=0; A2=0; A4=0 и т.д.
Таким образом, кривая, симметричная относительно оси абсцисс, выражается тригонометрическим рядом следующего вида:
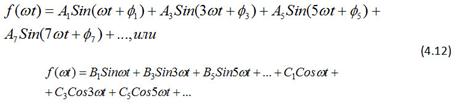
Симметрию относительно оси ординат имеют кривые, у которых при изменении знака аргумента величина и знак функции не меняются:

Симметрия относительно оси ординат

Функция, симметричная относительно оси ординат, не содержит синусов:
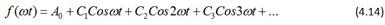
В этом можно убедиться без математического доказательства. Действительно, входящие в состав ряда косинусы симметричны относительно оси ординат, а синусы несимметричны. Если функция в целом симметрична относительно оси ординат, то это возможно лишь при отсутствии синусов. Наличие же постоянной составляющей не нарушает симметрии такого вида.
Симметрия относительно начала координат соответствует условию:

Нетрудно заметить, что в данном случае в обеих половинах периода имеются две равные по величине ординаты с разными знаками. Поэтому среднее значение функции за период, или постоянная составляющая, равно нулю. Отсутствуют и несимметричные относительно начала координат косинусоидальные составляющие.
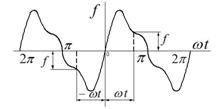
Симметрия относительно начала координат
 Функция имеет только ряд синусов, обладающих симметрией такого же характера, как и функция в целом:
Функция имеет только ряд синусов, обладающих симметрией такого же характера, как и функция в целом:

Совокупности коэффициентов ak,bk разложения периодической функции f(t) в ряд Фурье называют частотными спектрами этой функции. Спектр сигнала изображается двумя диаграммами, из которых одна называется амплитудно-частотным спектром (АЧС), а другая – фазочастотным спектром (ФЧС).




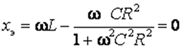




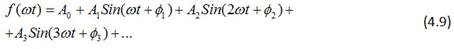
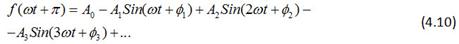
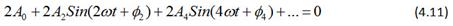
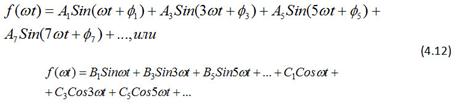


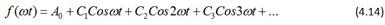


 Функция имеет только ряд синусов, обладающих симметрией такого же характера, как и функция в целом:
Функция имеет только ряд синусов, обладающих симметрией такого же характера, как и функция в целом:


